서론
선행연구 고찰
1. 선행연구 고찰
2. 선행연구와의 차별성
연구방법론
1. 연구의 내용 및 방법
2. Self Organizing Map
3. 입력변수 설정
방법론 적용 및 분석
1. 분석구간 및 자료
2. 중장기 통행시간 예측 분석결과
결론
1. 연구의 의의 및 결론
2. 향후 연구과제
서론
고속도로 교통정보는 도로운영자 및 이용자에게 중요한 요인으로 작용한다. 운영자 관점에서는 도로의 전반적인 교통상태를 확인할 수 있으며, 이용자 관점에서는 통행계획 수립과 통행경로 변경 등에 영향을 미친다. 특히 예측 교통정보는 도로에 집중된 교통수요를 분산시키는 효과를 가지며, DSRC (Dedicated Short-Range Communication, 근거리전용통신) 기반 하이패스 단말기를 통해서 가공 및 제공이 가능하다. DSRC 기반의 구간검지(section measurement) 자료의 경우 과거의 통행정보 수집의 지점검지(spot measurement)와 다르게 개별 차량의 통행정보 수집이 가능하다. 이는 개별차량 식별이 가능한 하이패스 단말기 번호를 통해서 연속된 시공간상의 통행경로 추정을 가능하게 한다(Kim et al., 2017; Lee and Kim, 2019). 이러한 통행경로 정보는 주요 구간의 다양한 이동경로를 추적할 수 있으며, 이를 활용한 교통관제 및 운영에 대한 필요성이 점차 증대되고 있다.
예측 교통정보는 크게 단기와 중장기로 나눌 수 있다. 단기 통행시간 예측은 실시간 자료를 기반으로 이용자가 통행을 시작하거나 통행 중일 경우 언제 목적지에 도착할지에 대한 예측정보를 제공한다. 일반적으로 1시간 이내의 예측을 단기예측으로 분류하며 단기 통행시간 및 교통량 예측 등의 다양한 선행연구가 진행되었다(Kim and Jang, 2013; Qiao et al., 2013). 중장기 통행시간 예측은 이용자가 사전에 통행을 계획하는 경우 소요시간 산출을 위한 예측 정보로 정의할 수 있다. 중장기 예측을 위한 데이터는 과거 통행 이력자료를 주로 이용하며, 이용자의 통행계획을 위한 정보들은 일반적으로 통행시작 하루 전 또는 일주일 전 등을 기준으로 요일 및 출발시각 단위로 제공이 가능하다. 따라서 중장기 예측은 변동성이 높은 단기예측 정보에 비해 일반적인 예측정보를 제공할 수 있으며, 이를 바탕으로 이용자가 본인의 통행과 관련된 의사결정(통행경로 선택, 출발시간 계획 등)을 효율적으로 하는데 활용될 수 있다. 일반적으로 1시간 이후 및 하루 등의 예측을 중장기예측으로 분류하며 중장기 통행시간 및 속도 등의 다양한 선행연구가 진행되었다(Jeong et al., 2015; Li et al., 2017; Chou et al., 2019). 최근까지 고속도로 통행시간 예측정보의 경우 단일 경로에 대한 도착예정시간 정보를 제공하는데 중점을 두고 있어, 이용자들의 실제 통행 의사결정에 도움을 주는 이동경로별 중장기 통행시간 예측에 대한 정보는 미흡한 측면이 존재한다.
이에 본 연구에서는 경로형 데이터 기반 이동경로별 중장기 통행시간 예측 연구를 실시한다. 이를 위하여 입력변수로 고속도로 통행시간에 영향을 주는 요소인 요일, 기상, 일 단위 교통량 등을 고려하고, 분석방법으로는 머신러닝 비지도학습(unsupervised learning)의 대표적 알고리즘인 자기조직화지도(Self Organizing Map, SOM)를 활용하여 예측을 실시한다. 이는 사전에 목표 값을 정의하지 않고 데이터 자체의 결합 및 유사성 등을 통하여 클러스터를 도출하는 방식으로 학습된 뉴런에 의해 교통패턴의 변화가 심한 경우에도 신뢰성 있는 예측정보 생성이 가능한 장점을 가진다.
논문의 구성은 다음과 같다. 2장에서는 기존 통행시간 예측과 관련된 문헌연구를 수행한다. 경로형 데이터 기반 중장기 통행시간 예측 방법론은 3장에 서술하였으며, 이를 활용한 이동경로별 통행시간 예측 결과는 4장에서 논의한다. 마지막 5장에서는 경로형 데이터 활용, 이동경로별 예측 통행시간, 그리고 향후 연구과제 등을 서술하였다.
선행연구 고찰
1. 선행연구 고찰
기존 고속도로 통행시간 예측의 경우 다양한 기법을 활용한 예상 도착시간에 대한 연구가 진행되었다. 대표적으로 회귀모형, 칼만필터(Kalman Filter), SVM (Support Vector Machine), 그리고 k-NN (k-Nearest Neighbor) 등을 활용한 연구들이 수행되었다.
회귀모형은 독립변수와 종속변수 사이의 선형 상관관계를 이용한 방법으로 고속도로 통행시간 예측 시 활용되었다. Kwon et al.(2000)의 연구에서는 회귀모형에 기반한 단계적 변수선택(stepwise variable selection method) 방식을 활용해서 고속도로 통행시간을 예측하였다. 분석결과 단기예측에는 현재의 교통상태를, 반대로 장기예측에는 과거이력자료를 활용하는 것이 효율적인 것으로 판단하였다. 하지만 본 회귀모형의 경우 단순회귀모형으로 site-specific한 단점이 존재하며, 단거리 구간에 대한 검증만 실시되는 한계를 보였다.
칼만필터 모형은 재귀적 추정 알고리즘으로 새로운 관측치를 활용하여 통행시간 상태변수를 지속적으로 업데이트하는 구조이다. 상태전이 모형(state transition model)에 의해 예측 및 추정과정이 수행되며, 오차 공분산을 최소화시키는 방식이다. 이전 시간대의 정보만을 활용하는 장점이 있으며, 실시간 예측에 우수한 정확도를 보였다. 하지만 예측 정확도가 상태전이 모형에 의존적이며, 각 시간간격에서 통행시간이 급변하는 경우 time-lag 등의 문제가 발생하는 단점을 보였다(Chen et al., 2004; Yang, 2005).
SVM 모형은 지도학습 기반의 선형분류 모형으로 주어진 데이터의 공간 경계를 찾는 알고리즘으로 고속도로 통행시간 예측에 적용되었다. 머신러닝 기법의 일환으로 최근 연속류 통행시간 예측에 다양한 연구들이 수행되었다. 하지만 SVM의 경우 이진분류에 적합한 알고리즘으로 파라미터 및 커널 선택에 민감한 단점을 가진다(Wu et al., 2005; Vanajakshi and Rilett, 2007; Long et al., 2019).
k-NN 모형은 대용량 이력자료 기반의 유사패턴을 이용한 예측기법으로 고속도로 통행시간 예측 시 활용되었다. 유사도 측정(similarity measure)을 위해서 일반적으로 유클리드 거리 함수를 사용하며, 해당 거리 유사도에 따라 과거 이력자료와의 매칭이 이루어진다. 본 모형은 각 단계별 파라미터 설정(이력자료 평활화, 유사도 함수, k개수, 예측 함수 등)이 예측 정확도에 중요한 요인으로 작용한다(Kim et al., 2016b). Tak et al.(2014) 연구에서는 글로벌매칭 및 로컬매칭을 포함한 Multi-level k-NN 모형을 제안하였으며, 각 매칭 단계에서 과거 대용량 이력자료를 유사도에 기반하여 예측 후보군을 최적화시키는 방식을 활용하였다. Qiao et al.(2013) 연구에서는 유클리드 거리를 활용한 유사도 산정 시 발생하는 문제점을 제시하고 Trend를 반영할 수 있는 개선 k-NN 모형을 제안하였다. 개선 k-NN 모형은 Trend 반영을 통한 유사 이력자료 매칭으로 ARIMA (Auto Regressive Integrated Moving Average), kaman filter 모형에 비해서 높은 정확도를 보였다.
SOM 모형은 주어진 입력 패턴에 대하여 자기 스스로 학습하는 비지도학습 알고리즘으로 중장기 버스 통행시간 예측에 활용되었다. Lee et al.(2017) 연구에서는 출발시간, 요일, 기온, 날씨 등을 입력변수로 상습 지 ‧ 정체 구간을 포함하는 광역버스에 대한 중장기 통행시간 예측을 수행하였다. 예측 정확도 분석결과 SOM 방법이 평균운행속도 기반 알고리즘에 비해서 기상상황(맑음/우천)에 따라 개선되는 결과를 보였다.
2. 선행연구와의 차별성
선행연구검토에서 확인할 수 있듯이 고속도로 통행시간 예측을 위한 다양한 연구가 수행되었으나 대부분의 연구에서 단기 통행시간 예측을 목적으로 수행되었다. 본 연구는 이용자의 통행계획에 활용되는 중장기적 관점의 통행시간 예측 기법을 제시하는데 차별성이 존재한다. 특히 개별차량 식별이 가능한 하이패스 단말기 번호를 통해서 시공간의 통행경로를 추정할 수 있으며, 이를 활용한 주요구간의 이동경로별 통행시간 예측정보 연구의 필요성이 존재한다. 선행연구에서 사용한 방법론 중 회귀모형의 경우 site-specific한 단점을 가지며, 칼만필터 모형은 현재 시점의 자료만 활용하기 때문에 예측의 정확도가 상대적으로 낮다. SVM 모형은 파라미터 및 커널선택에 민감한 단점을 가지며, k-NN 모형도 각 단계별 파라미터 설정에 따라 예측 정확도가 민감하였다. 이에 본 연구에서는 다양한 입력변수를 활용하여 데이터 자체의 유사성을 스스로 학습할 수 있는 장점을 가진 비지도학습 기반의 SOM 알고리즘을 활용하여 중장기 고속도로 통행시간 예측을 실시한다. 또한 본 연구에서는 중장기 통행시간 예측 시 영향을 주는 요소들을 기존 문헌 검토를 통해 선정하여 요일(주중, 주말, 공휴일), 기상요인(강수량), 일 단위 교통량 등을 추가적으로 고려하여 분석을 실시한다.
연구방법론
1. 연구의 내용 및 방법
경로형 데이터는 개인의 이동 궤적을 확인할 수 있는 시공간상의 연속적인 동적자료로써 기존의 지점 및 특정 구간의 교통정보와는 다른 연구방법 적용이 필요하다. 경로형 데이터를 활용해서 개별 차량의 기종점 통행 경로에 대한 정보를 가공할 수 있으며, 동일한 기종점임에도 서로 다른 경로를 이용하기 때문에 중장기 고속도로 통행시간 예측을 위해서는 이를 반영한 모형의 구축이 필요하다.
이에 본 연구에서는 SOM 클러스터링 기법을 이용하여 통행시간과 관련된 변수들 간의 유사성을 파악하여 경로에 따른 대표 통행시간을 도출 및 예측하고자 한다. 중장기 고속도로 통행시간 예측 모형 구축을 위해 본 연구에서는 먼저 학습에 사용될 입력자료를 수집하고 구축한다. 어떠한 변수들이 고속도로 통행시간에 영향을 미치는지에 대해 기존에 수집되어있는 경로형 데이터를 분석하고, 기존 문헌들에서 유의미한 영향을 미치는 변수들을 검토하여 통행시간 예측을 위한 입력자료를 구성한다. 이를 바탕으로 클러스터링 분석을 통해 경로별로 비슷한 통행시간을 가지는 변수들의 조합을 찾는다. 클러스터링은 2단계로 수행되는데, 1차적으로 SOM을 통해 다차원 변수들에서 유의미한 특징으로 차원을 축소한다. 최종적인 클러스터 수를 찾기 위해 2번째 단계로 K-means 클러스터링을 수행한다. 이후 클러스터별 대표 통행시간을 산출하고 각 경로별로 통행시간들이 어떻게 분포하는지 분석한다. 도출된 모형의 예측 정확성을 평가하기 위해 기존에 사용하던 k-NN 예측 모형과 비교한다. 연구의 과정을 요약하면 Figure 1과 같다.
2. Self Organizing Map
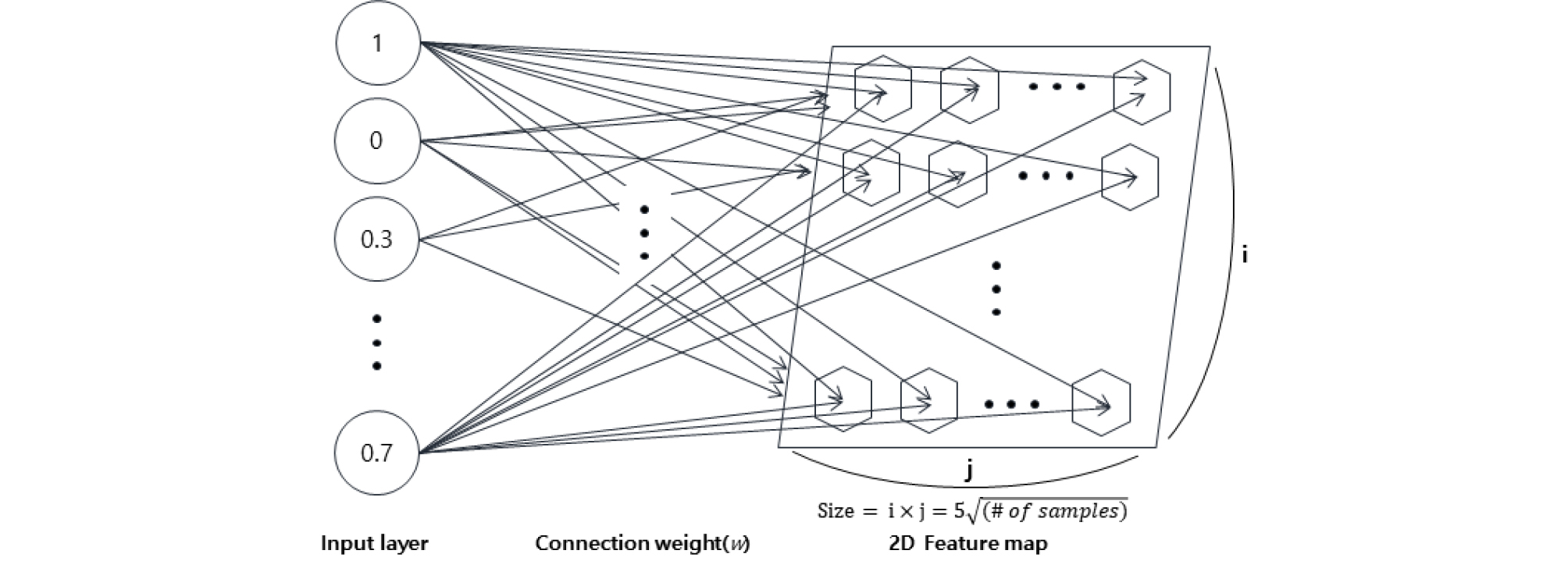
SOM은 Kohonen(1990)이 제시했던 인공신경망을 활용하는 클러스터링 기법의 일종으로, 고차원의 데이터를 2차원의 지도형태로 차원을 축소하여 지도형태로 시각화하여 클러스터링을 수행한다. 따라서 분석 대상 고차원 데이터가 어떤 식으로 그룹화 되어 있는지 시각적으로 표현할 수 있어 다양한 분야에서 사용하고 있다. SOM을 통한 클러스터링기법은 인공신경망 기반으로 비슷한 패턴들을 기존 알고리즘보다 효과적으로 분류 가능하며, 대용량 데이터에 대하여 클러스터 분류 속도가 빠르고 기존 클러스터링 알고리즘 대비 국지 최소값 문제 및 이상값에 민감하지 않다는 장점이 있다(Vesanto, 1999). SOM에서 클러스터링은 사전에 정의된 크기의 2차원의 평면 특징지도(feature map)를 구성하고 있는 뉴런들에 분석 대상 데이터들을 연결시켜 각 뉴런들이 클러스터 중심의 역할을 수행하게 된다. 자기조직화지도의 기본적인 구조는 Figure 2와 같다.
특징지도를 구성하는 뉴런의 수는 (n은 입력 샘플 수)의 식으로 정해지며, 각 차원의 크기는 입력 샘플 수와 특징 값의 행렬에서 얻어지는 고유값의 비율을 통해 나눠져 특징지도를 만든다. SOM의 클러스터링 과정은 다음과 같다. 입력층과 특징지도 뉴런들 간의 연결강도 w를 랜덤하게 초기화하고, 이를 이용하여 입력데이터와 모든 뉴런들 간의 유클리디안 거리를 계산한다. 이 중 가장 가까운 거리의 뉴런을 해당 입력데이터의 클러스터(Best Matching Unit, BMU)로 선택한다. 위와 같은 방법으로 모든 입력데이터에 대해 BMU를 찾고, 주어진 w에 대해 얼마나 뉴런들이 분산되어 있는지 계산하여 분산을 늘리는 방향으로 연결강도를 수정한다. 전체 과정을 w의 변화가 충분히 적어질 때까지 수행하여 클러스터링을 종료한다. 본 연구에서는 대용량의 데이터를 클러스터링 하기 때문에 특징지도의 크기가 지나치게 커져 통행패턴이 지나치게 세분화 되어 해석이 어려워지고 실적용에 비효율이 발생할 수 있으므로, 학습이 완료된 특징지도에 대해 K-means 클러스터링을 수행하여 통행패턴의 개수를 최종적으로 확정할 수 있다. 최종 클러스터수를 판단하기 위해서는 클러스터 간 분산과 클러스터 내 분산의 비율을 통해 그룹화 정도를 수치화할 수 있는 Calinski-Harabasz Index를 이용하였다(Caliński and Harabasz, 1974). 클러스터 중심 개수인 K의 수를 점차 늘려가면서 Calinski-Harabasz Index가 가장 큰 값일 때의 클러스터 수가 주어진 데이터를 가장 잘 설명하는 클러스터 수라고 판단할 수 있다.
3. 입력변수 설정
본 연구에서는 DSRC 기반 개별 차량의 하이패스 단말기 번호를 이용해서 경로형 데이터를 구축한다. 수집된 개별 차량의 데이터를 RSE 위치 및 시간 순으로 정렬하여 각 차량의 이동경로별 통행시간을 가공한다. 이후 클러스터 분석을 위해서 해당 경로형 자료에 추가적인 변수들을 추가하여 2차 가공을 수행한다. 통행시간 예측 정확도를 높이기 위해 기존 문헌들을 검토하여 통행시간에 영향을 미치는 추가적인 변수들을 선정하였다. 정보 제공 효율성 측면에서 현재 출발하는 이용자를 대상으로 통행특성을 반영한 예측이 필요하므로(Rice and Van Zwet, 2004; Kim, 2009) 출발시각을 1시간 단위로 가공하였고, 현재 한국도로공사에서 제공하고 있는 일 단위 교통량을 입력변수로 활용하였다(Korea Expressway Corporation). 또한 통행패턴은 요일 ‧ 시간대와 같은 시간변수에 따라 반복적으로 나타나는 패턴과 휴일 ‧ 명절과 같이 특정한 일시에 나타나는 효과가 존재하므로(Shin et al., 2014; Kim et al., 2016a) 요일 및 연휴 등을 나타내는 요일코드를 선정하였다. 해당 요일코드의 경우 한국도로공사에서 정의한 다양한 패턴이 요일특성(앞뒤 요일 패턴분석을 위해 일자마다 부여된 고유 코드)을 고려한 Pcode를 활용한다(Korea Expressway Corporation, 2017). 추가적으로 기상요인 중 샘플수가 많고 통행 변동 및 속도에 영향을 미치는 강수 여부(Nookala, 2006; Jeong et al., 2013; Kim and Kim, 2015)를 우천 여부에 따라 바이너리(Binary)값으로 가공하였으며, 서울-대구 구간의 특성을 반영하기 위해서 주요 지역(서울, 대전, 대구)에서 수집된 기상정보를 활용하였다. 추가적으로 학습된 모델 검증에는 일 단위 교통량을 사용할 수 없으므로, 한국도로공사에서 개발한 다중회귀모형 기반의 일 단위 교통량 예측 모형에서 산출된 값을 활용하였다(Korea Expressway Corporation, 2017). 입력자료 중 연속된 값이 아닌 이산형 데이터의 경우에는 각각에 대해 One hot encoding을 수행하였다. One hot encoding은 이산형데이터를 신경망에 입력할 때 이용하는 기법으로, 각 이산형 데이터의 카테고리 수에 따라 1,0으로 이루어진 이진수로 변환하여 벡터의 크기를 늘려 표현하는 방식이다. 이렇게 구축된 모든 값은 0-1사이의 값으로 정규화하여 클러스터링의 입력자료로 이용하였다. 클러스터링 분석에 사용된 입력데이터들을 정리하면 Table 1과 같다.
Table 1. Input data description
방법론 적용 및 분석
1. 분석구간 및 자료
본 연구에서는 중장기 통행시간 예측을 위해서 서울-대구 구간의 경로형 데이터를 이용한다. 경로형 데이터는 DSRC 기반으로 수집된 개별 차량의 데이터로 고속도로 본선 도로에 설치된 노변검지기(Roadside Equipment, RSE)를 통해서 활용이 가능하다. 특히 개별 차량의 통행경로를 추정하기 위해서 하이패스 단말기 번호 활용이 가능하며, 이를 통해 식별된 개별 차량의 통행데이터를 RSE 위치 및 시간 순으로 정렬하여 분석하였다(Lee and Kim, 2019).
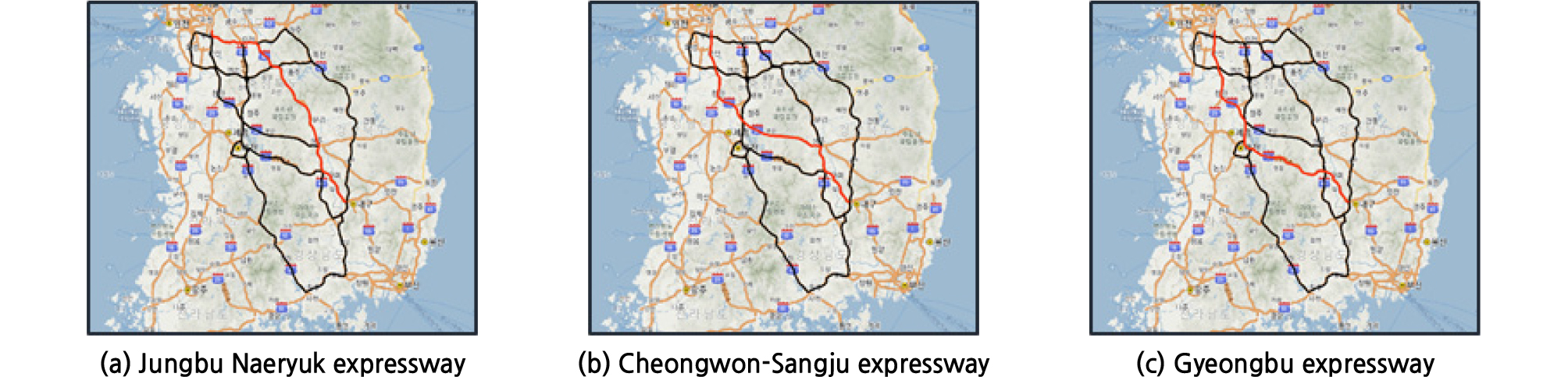
이에 본 연구에서는 서울-대구 구간의 경로형 데이터를 활용해서 중장기 통행시간 예측을 실시한다. 분석 통행경로는 서울-대구 구간의 여러 가능한 경로들 중에서 대부분의 이동경로를 차지하는 중부내륙, 청원-상주, 그리고 경부선 등이며, 승용차 통행자료만 활용한다(Figure 3 참조). 중장기 예측을 위한 이력자료는 2017.1.1.-2017.11.31 (11개월)이며, 테스트 자료는 평일, 주말, 공휴일을 포함하는 2017.12.15.-21, 2017.12.25. (7일)로 설정한다. 본 예측 알고리즘 결과에 대한 비교 ‧ 검증을 위해서 Multi-level k-NN (Tak et al., 2014)을 사용하였으며, 예측 시간간격은 1시간이다. Multi-level k-NN은 크게 3가지 단계를 포함하고 있으며, Layer 1 (classification)에서는 요일 및 날씨에 대한 구분, Layer 2 (global matching)에서는 후보군의 날짜를 줄이는 과정으로 TCS 및 VDS 교통량 기반의 패턴매칭, 마지막으로 Layer3 (local matching)에서는 최종 후보군 날짜를 줄이는 과정으로 VDS 점유율 및 속도, DSRC 통행시간 등이 활용된다.
2. 중장기 통행시간 예측 분석결과
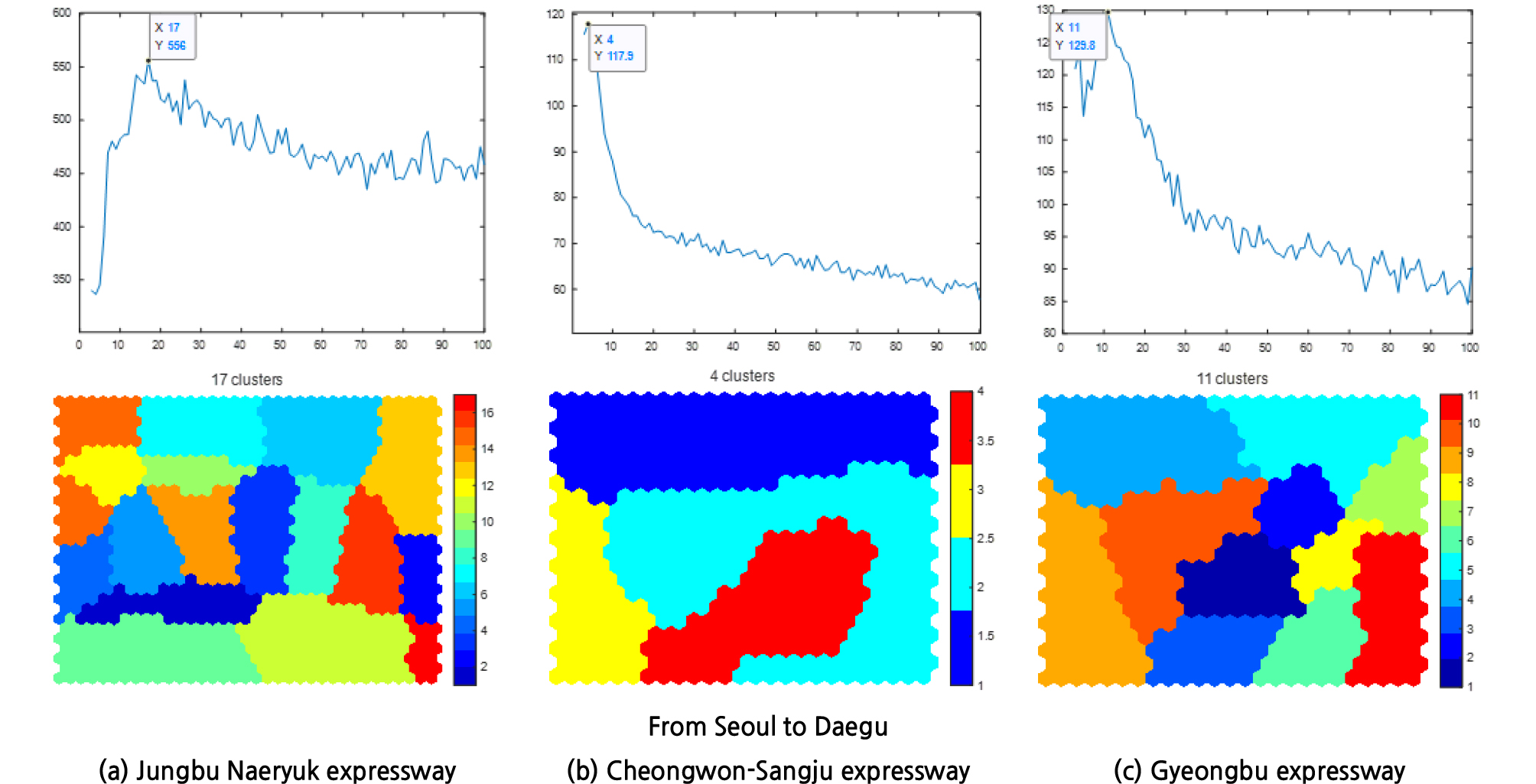
구성된 입력데이터를 분석 대상 경로별로 클러스터링을 수행하여 각 클러스터별 대표 값 테이블을 생성하였다. 중부내륙, 청원-상주, 경부선으로 구성된 3가지 경로이므로 서울-대구 통행으로 총 3개의 참조 테이블을 이용하여 예측 결과와 비교하였다. 각 경로마다 차량 대수는 차이가 존재하나 1시간단위로 통합된 통행시간 데이터를 이용하였으므로 입력데이터의 행의 개수는 모두 같다. 따라서 같은 크기의 자기조직화 지도를 이용하였으며, 클러스터 분석은 각 경로별로 구분하여 수행하였다. Figure 4에서 분석대상 3개 경로에 대해 자기조직화지도와 K-means 클러스터링을 이용하여 Calinski-Harabasz Index를 계산한 클러스터링 결과를 요약하였다.
각 경로별 상단부의 그래프는 클러스터수를 2부터 100까지 증가시켜가며 계산된 Calinski-Harabasz Index를 나타내며, 가장 결과가 좋은 최대값을 표시하였다. 중부내륙 경로의 경우 17개, 청원-상주 경로의 경우 4개, 경부 고속도로 경로의 경우 11개로 클러스터를 구분하였을 때 해당 데이터를 가장 잘 설명하는 결과로 해석할 수 있다. 적정 클러스터 수를 도출한 결과 경로 및 방향에 따라 클러스터의 개수가 상이함을 알 수 있었다. 최소 4개에서 최대 17개까지의 편차를 보였다. 이는 각 경로별로 통행패턴의 차이가 상이하다는 것으로, 크러스터 수가 많을수록 통행패턴이 다양함을 나타낸다. 클러스터별 대표 통행시간 산출을 위해 각 클러스터별로 중심에 가장 가까운 뉴런에 속하는 값들의 중간 값을 이용하여 경로별로 Table 2와 같은 결과를 얻었다.
Table 2. Prediction accuracy by different routes
클러스터별 대표 통행시간의 편차는 경로에 따라 상이했다. 클러스터수가 가장 작은 4개의 경우에도 최대 최소 통행시간 차이는 15분 이상의 차이를 보였다. 클러스터 수가 많아질수록 통행시간 패턴이 더 다양해지기 때문에 17개의 패턴을 가지는 중부내륙 고속도로 이용 통행의 경우는 30분 이상의 차이를 가지고 있다. 도출된 모형의 정확도 검증을 위하여 클러스터링에 이용하지 않은 12월 이력자료 중 테스트 데이터로 선정한 7일간의 자료에 대하여 경로 ‧ 시간별로 학습된 클러스터 지도에 투사하여 통행시간을 예측하였다. 이를 이용하여 실제 통행시간 및 기존 방법론과 정확도를 Equation 1과 같은 MAPE (Mean Absolute Percentage Error)로 비교하였다.
| $$MAPE(\%)=\frac{100\%}n\sum_{i=1}^n\left|\frac{(TT_i-PTT_i)}{TT_i}\right|$$ | (1) |
: actual travel time
: predicted travel time
각 경로별 요일 특성에 따라 실제 통행시간과의 차이 비교는 평일, 주말, 공휴일로 나누어 수행하여 Table 3으로 정리하였다. 선행연구들의 다양한 예측기법들 중에서 가장 높은 정확도 및 일반적으로 활용되는 k-NN 모형과 정확도를 비교하였다.
Table 3. Prediction accuracy of different algorithms
정확도 분석 결과 경로별 요일특성에 따른 MAPE는 전반적으로 본 연구에서 제시한 클러스터 기반의 통행시간 예측 모형이 k-NN 모형 대비 예측 정확도가 우수함을 확인하였다. 특별히 서울-대구 통행 경로 중에서 가장 많은 통행을 가지는 중부내륙 고속도로는 k-NN 모형과 비교할 때 평일 18.30%→10.24%, 주말 20.85%→12.45%, 공휴일 22.30%→11.20% 등 높은 오차감소를 보였다. 그리고 청원-상주 고속도로 및 경부고속도로의 경우에도 요일특성에 따른 정확도 비교 시 전반적으로 개선된 예측 결과를 보였다. 이와 같이 본 연구 방법론을 활용하여 경로형 자료를 기반으로 고속도로 통행시간 예측 시 기존보다 더 정확한 정보 제공이 가능하다. 이는 기존 k-NN 알고리즘의 경우 경로단위 예측 시 링크단위로 생성된 중장기 예측 테이블에 기반해서 시공간 통행경로에 따른 예측 통행시간의 합으로 산정되는데, 교통량 증가 등으로 인한 혼잡발생 시 통행시간 합산 과정에서 발생되는 통행시간 증가분에 대한 반영이 어려워 예측의 정확도가 감소하는 요인으로 판단된다. 본 연구에서 제시한 방법을 활용한 정확한 통행시간 예측 정보는 이용자들이 통행계획을 세울시 신뢰도 높은 참고자료로 활용 가능하며 다양한 경로에 대한 안내가 가능하므로 국내 고속도로를 보다 효율적으로 이용하는데 기여할 수 있을 것으로 기대된다.
결론
1. 연구의 의의 및 결론
본 연구는 DSRC 기반 경로형 데이터를 활용하여 중장기 통행시간 예측 연구를 수행하였다. 기존 통행시간 예측 연구는 대부분 단기 예측을 목적으로 수행되어 이용자의 통행계획에 활용되는 중장기적 관점의 통행시간 예측에는 한계가 존재했다. 이에 본 연구에서는 개별차량 식별이 가능한 하이패스 단말기 번호를 활용해서 연속된 시공간상의 개별 차량의 통행경로를 추정하였으며, 이를 활용해서 이동경로에 따른 중장기 통행시간 예측 연구를 수행하였다. 먼저 기존 통행시간 예측 연구들의 사례 검토를 통해서 본 연구에 적용되는 SOM 방법론에 대한 유용성을 검토하였고, 각 단계별 세부절차 및 변수결정, 입력자료 구축, 그리고 클러스터 과정 등을 제시하였다. 특히 예측의 정확도 개선을 위해서 통행시간에 영향을 주는 요소인 요일특성, 기상, 일 단위 교통량 등을 입력변수로 고려하여 분석을 수행하였다. 분석에 사용된 경로형 데이터는 서울-대구 구간이며, 해당 구간에서 대부분의 이동경로를 가지는 중부내륙, 청원-상주, 그리고 경부선 등을 분석구간으로 선정하였다. SOM 학습에 사용된 이력자료는 2017.1.1.-2017. 1.31 (11개월)이며, 테스트 자료는 평일, 주말, 공휴일을 포함하는 2017.12.15.-21, 2017.12.25. (7일)을 사용하였다. 구성된 입력데이터에 기반하여 경로별로 클러스터 분석을 수행하였으며, 각 클러스터별 대표 값에 따른 참조표 생성, 그리고 k-NN 예측결과와 정확도 비교를 통한 유효성 등을 검증하였다.
본 연구는 기존의 단기적 링크기반의 통행시간 예측의 부정확한 한계를 극복할 수 있는 방법으로 신뢰성 있는 중장기 통행시간 예측정보를 제공할 수 있다. 특히 이동 경로별 통행시간 예측정보를 제공함으로써 개별 통행자의 경로선택 및 출발시간 선택 등에 유용하게 활용되어질 수 있다. 향후 고속도로 주요 권역별 이동경로에 대한 데이터 구축 및 주기적인 SOM 알고리즘 학습이 선행된다면, 중장기 통행시간 예측의 정확도 개선과 함께 탄력적인 교통운영 및 관제가 가능할 것으로 판단된다.
2. 향후 연구과제
본 연구에서 활용한 SOM기반 중장기 통행시간 예측 알고리즘은 예측 정확도가 우수하나 주요 권역별로 이동경로에 따른 예측겨로가 제공을 위해서는 각 경로별로 참조테이블을 구성하여야한다는 한계가 존재한다. 따라서 전국단위의 서비스 확장을 위해서는 각 테이블 구성을 위해 모델을 개별적으로 학습시켜야하므로 데이터 가공 및 모델 생성에 시간이 많이 걸린다. 이에 동일한 패턴을 보이는 경로들을 사전에 분석하여 통합 모델을 통해 학습이 필요한 모델을 줄이는 연구가 필요하다. 또한 본 연구에서는 이력자료 학습에 11개월간의 자료만을 활용하였는데, 추후 보다 많은 양의 이력자료를 확보하여 기상상황이나 일 단위 예측교통량에 따른 예측 정확도 비교를 통한 모델 검증 수행이 필요하며, 다양한 교통패턴 및 유고상황 등에 대한 범용성 확보가 가능한 고도화된 모델을 생성할 수 있을 것으로 판단된다.