Queue Length Estimation Algorithm for Signalized Intersections Using Taxi DTG Data

Minhyoung Lee; Youngchan Kim

doi:10.7470/jkst.2020.38.1.068

Preview

Article

Journal of Korean Society of Transportation. 29 February 2020. 68-83
https://doi.org/10.7470/jkst.2020.38.1.068

Queue Length Estimation Algorithm for Signalized Intersections Using Taxi DTG Data

신호교차로에서 택시 DTG 자료를 활용한 대기행렬 길이 추정 알고리즘 개발

Minhyoung LEE¹^*

Youngchan KIM²

이 민형¹^*

김 영찬²

¹Senior Researcher, Traffic Science Institute, Korea Road Traffic Authority, Wonju 26466, Korea

²Professor, Department of Transportation Engineering, University of Seoul, Seoul 02504, Korea

¹도로교통공단 교통과학연구원 선임연구원

²서울시립대학교 교통공학과 교수

^{* Corresponding Author}

License (open-access):

Ⓒ Korean Society of Transportation. This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

In this study, an algorithm was developed for estimating the queue length at signalized intersections using taxi DTG data collected for the Metropolis of Seoul. For this, the coordinates of individual vehicles plotted on a time-space diagram were estimated from individual vehicles experiencing speed variations owing to traffic signals at intersections. To estimate the queue length at signalized intersections, the speed of the forming queue shockwave was estimated from vehicle coordinates at locations of speed deceleration for every cycle. The microsimulation software Vissim was used to verify the accuracy and sensitivity of the proposed algorithm. The results of the evaluation revealed at least 19.8% of the mean absolute percentage. The result indicates that the queue length can be estimated through this approach.

Keywords

queue length

shockwave

signalized intersection

simulation

taxi DTG data

대기행렬 길이는 신호교차로의 운영을 위한 중요한 효과척도이다. 서울시에서는 택시 DTG 자료를 통해 개별 차량의 주행정보를 수집하고 이를 활용하여 교통정보를 생성하고 있다. 본 논문에서는 개별 택시에서 수집된 DTG 자료 중 위치정보를 활용하여 신호교차로에서 대기행렬 길이를 추정하기 위한 알고리즘을 개발하였다. 위치정보를 통해 시공도상에 개별 차량의 속도변화가 발생되는 지점을 추정하였으며 대기행렬 길이를 추정하기 위해 매주기 추정된 개별 차량의 속도감소 지점들을 활용하여 대기행렬이 생성되는 충격파의 속도를 산정하였다. 제안 된 알고리즘의 정확성을 검증하기 위해 마이크로시뮬레이션 소프트웨어를 사용하였다. 평가 결과 평균절대비율오차가 19.8%를 나타내어 택시 DTG 자료를 활용하여 대기행렬 길이를 추정할 수 있음을 확인하였으며 프로브차량 비율에 따른 알고리즘의 민감도를 분석하였다. 본 연구는 향후 개인정보 보호법의 개정에 따라 현장자료를 활용한 추가적인 연구가 수행된다면 신호교차로의 운영 및 정책결정에 활용될 수 있을 것으로 기대된다.

키워드

대기행렬 길이

충격파

신호교차로

시뮬레이션

택시 DTG 자료

MAIN

서론
이론적 고찰
1. 신호교차로의 개별 차량 지체
2. 대기행렬 길이의 정의
3. 대기행렬 길이 추정
알고리즘 개발
1. 개별 차량의 제어지체 추정
2. 개별 차량의 좌표 추정
3. 충격파 추정 및 대기행렬 길이 산정
4. 도착률 변화를 고려한 대기행렬 길이 산정
알고리즘 모의실험
1. 모의실험 환경구축
2. 모의실험 결과분석
결론

서론

1903년 우리나라에 자동차가 처음 등장한 이래로 자동차 등록대수는 경제성장과 함께 지속적으로 증가하였으며, 2017년에는 2천 2백만 대를 초과하였다. 이로써 우리나라는 2.3명당 1대의 자동차를 소요하게 되었으며(MOLIT, 2017), 차량 수의 지속적인 증가로 인해 교통사고 및 환경오염 등과 같은 사회적 부작용과 함께 교통 혼잡으로 인한 막대한 사회적 비용이 발생하게 되었다.

2015년 국내 교통혼잡비용은 국내 총생산(GDP)의 2.13%로 추정되며, 미국이 국내 총생산 대비 교통혼잡 비용이 0.83%를 차지하는 것과 비교할 때 교통 혼잡으로 인한 사회적 손실이 크게 발생하고 있음을 알 수 있다. 특히, 서울을 비롯한 6대도시에서 발생하는 총 교통혼잡비용은 지방부 도로의 2배에 달하지만 대부분의 국가 도로 건설 프로젝트에 대한 투자는 정부정책에 따라 지방부 도로에 사용되고 있다(Sung et al., 2012).

교통혼잡은 병목, 공사구간, 기상 조건 및 교통사고와 같은 다양한 요인에 의해 발생하지만 지방부 도로와 달리 도시부 도로에서는 신호교차로의 비효율적인 운영이 교통체증을 악화시키는 주요 요인 중 하나이다.

지능형교통체계(Intelligent Transport Systems, ITS)는 교통시설의 이용을 극대화하고 교통수단의 수송효율을 높이는 한편, 국민의 교통편의 증진과 교통안전을 도모할 수 있도록 교통체계의 운영 ‧ 관리를 자동화 ‧ 과학화하는 체계를 의미한다. 과거 교통정보 수집시스템의 수집범위는 특정 지점으로 제한되어 구간을 대표하는 정보로 활용하기에 한계가 있었으며, 공공기관의 주도로 추진된 인프라 기반의 구간 교통정보 수집시스템의 경우 많은 인프라 투자비용과 적정 프로브차량 확보문제로 인하여 교통정보의 수집량 및 수집범위에 한계가 있었다(Jang et al., 2015). 그러나 최근 GPS (Global Positioning System)가 장착 된 스마트폰의 빠른 확산으로 지점 및 인프라 기반의 구간정보 수집시스템의 문제점을 극복한 양질의 지속 가능한 교통정보 제공이 촉진될 것으로 기대되며 4차 산업혁명 시대의 도래와 함께 빅데이터의 활용에 대한 활용방안이 요구되고 있다.

우리나라는 2010년 교통안전법 시행령 개정에 따라 모든 상업용 차량에 GPS가 장착된 디지털운행기록저장장치(Digital Tachograph, DTG)의 설치를 의무화 하였다. 현재 서울시에는 디지털운행기록저장장치를 장착한 약 60,000대의 택시가 운영되고 있으며, 개별 택시는 매 10초마다 개별 차량의 위치정보를 수집하여 150초마다 교통정보센터(TOPIS)로 전송하고 있다(Han and Kim, 2017).

신호교차로의 운영효율을 평가하기 위해 일반적으로 신호제어의 영향이 고려된 차량 당 제어지체가 사용된다. 하지만 신호교차로에서 제어지체를 산출하기 위해서는 교통량 정보가 필수적이므로 인프라 및 GPS를 활용한 프로브차량 기반의 정보수집 체계에서는 활용이 불가능하다. 대기행렬 길이는 지체, 통행시간, 서비스 수준(Level of Service)등과 함께 신호교차로의 운영효율을 평가할 수 있는 중요한 효과척도로서 신호교차로의 효율적인 운영을 위해 다양한 교통정보를 활용한 대기행렬 길이 추정방법이 연구되었다. 따라서 본 연구에서는 현재 서울시에 수집하고 있는 택시 DTG 자료를 신호교차로의 효과척도로 활용하기 위한 신호교차로의 대기행렬 길이를 추정하는 알고리즘을 개발하고 개발된 알고리즘의 효과를 평가하였다.

이론적 고찰

1. 신호교차로의 개별 차량 지체

교차로는 상충되는 이동류가 교차하는 지점으로 안전과 효율을 달성하기 위해 적절한 수준의 제어가 수반되어야 한다. 따라서 교차로에 접근하는 차량은 교통안전시설의 지시에 따라 통행의 우선권을 부여받고 안전하게 교차로를 통과하게 된다.

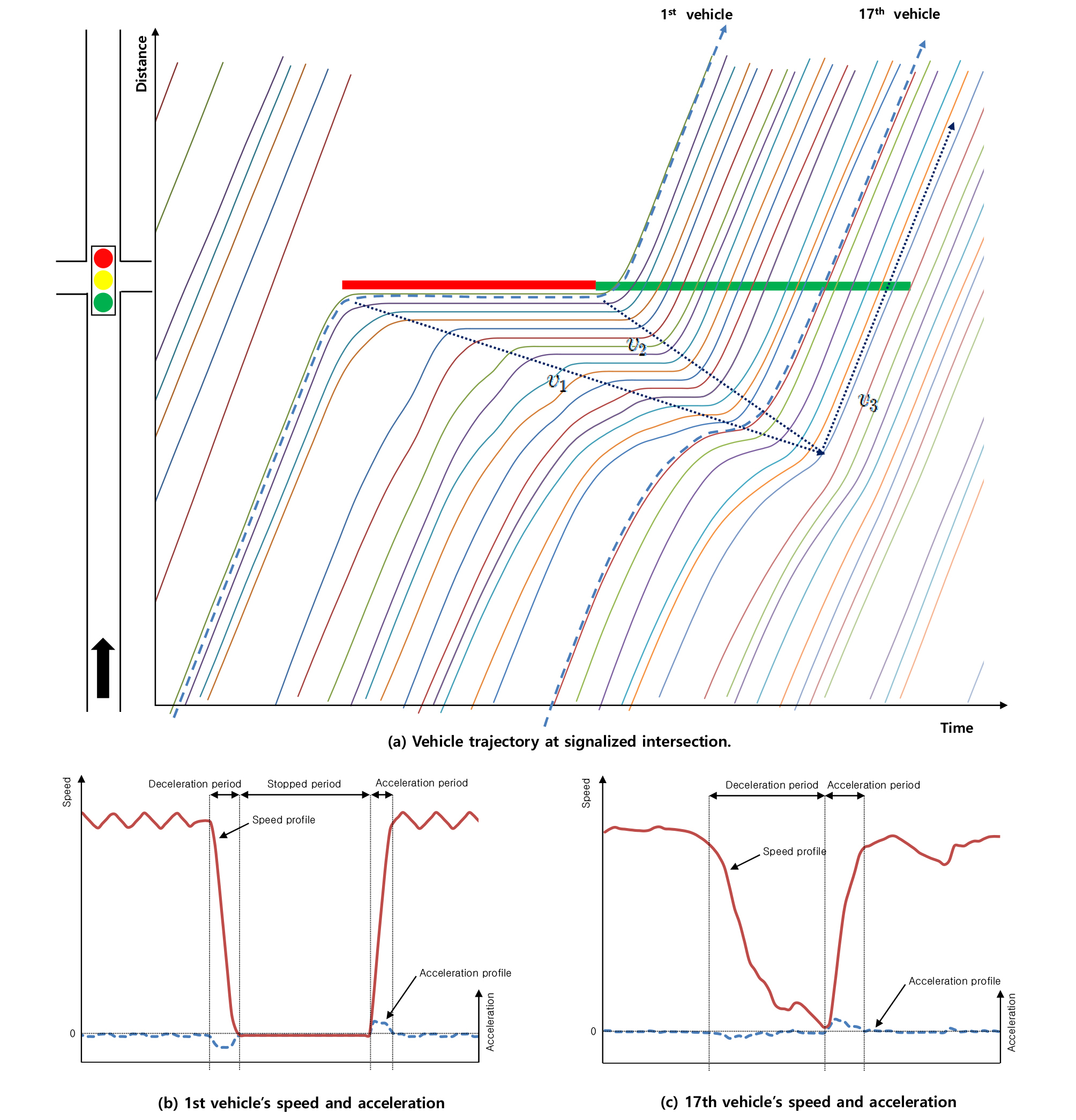
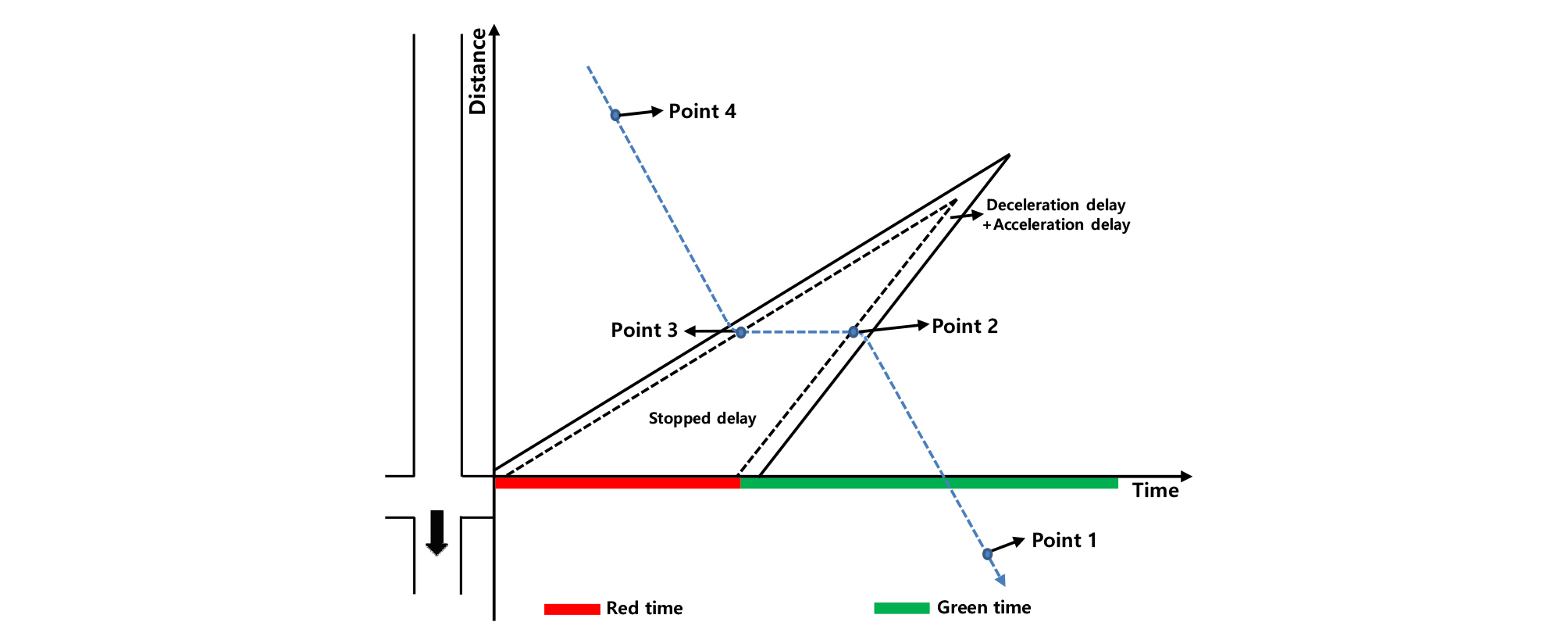
신호교차로를 평가하는 주요 효과척도에는 제어지체, 대기행렬 길이 및 정지 횟수 등이 사용되며 일반적으로 Highway Capacity Manual 6th Edition (TRB, 2016)(HCM)에서 제시하는 제어지체(Control delay)가 가장 널리 사용된다. 제어지체는 신호제어로 인해 차량이 속도를 줄이거나 정지함에 따라 발생하는 통행시간의 증가분을 의미하며, 개별 차량이 신호기에 의해 속도감소를 경험한 통행시간과 그렇지 않은 통행시간의 차를 통해 추정 할 수 있다. 제어지체는 가 ‧ 감속지체(Acceleration-deceleration delay)와 개별 차량이 대기행렬에 포함된 시점부터 정지선을 통과하는 시점까지의 시간 간격을 의미하는 대기행렬지체(Time-in-queue delay)의 합으로 표현 될 수 있다(Roess et al., 2011). Figure 1에서 첫 번째 차량의 경우 완전히 정지하여 대기행렬에 포함되므로 가속 및 감속지체 및 대기행열지체의 합으로 개별 차량의 제어지체를 표현 할 수 있다. 하지만 17번째 차량은 차량이 완전히 정지하지 않아 차량의 대기행렬 포함 유무를 결정하는 속도기준에 따라 대기행렬지체를 포함하지 않고 가 ‧ 감속지체 만을 개별 차량의 제어지체로 가질 수 있다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F1.jpg

Figure 1.

Individual vehicle trajectory and speed profile at a signalized intersection

따라서 신호교차로에서 대기행렬 길이를 추정하기 위해서는 개별 차량이 경험하는 제어지체의 구성요소를 명확히 구분하야하며 대기행렬에 합류하는 개별 차량의 속도에 대한 명확한 기준이 요구된다.

2. 대기행렬 길이의 정의

HCM에서는 대기행렬을 시스템 서비스를 받기 위해 정지하여 대기하는 차량과 함께 대기행렬의 끝에 저속으로 합류하는 차량을 대기행렬의 일부로 정의하고 있다. Liu et al.(2012)은 대기행렬을 완전히 정지한 차량의 대기열인 정지대기행렬(Standing Queue)과 신호 또는 정지대기행렬로 인해 속도의 변화가 발생하는 차량의 행렬인 이동대기행렬(Moving Queue)의 합으로 나타내었다. 그러나 HCM에서는 대기행렬에 포함되는 차량의 속도기준을 정의하고 있지 않으며, 미시적 교통시뮬레이션 소프트웨어의 경우 대기행렬 길이 또는 대기차량의 수를 Table 1과 같이 다양한 속도기준을 통해 결정하고 있다(FHWA, 2007).

Table 1. Default speed considered for vehicles in a queue

Simulation software	Description
SimTraffic	≤10ft/s (10.9Km/h)
CORSIM	≤3ft/s (3.3Km/h)
Vissim	≤5Km/h
Paramics	≤2m/s (7.2Km/h)
Aimsun	User-specified threshold speed

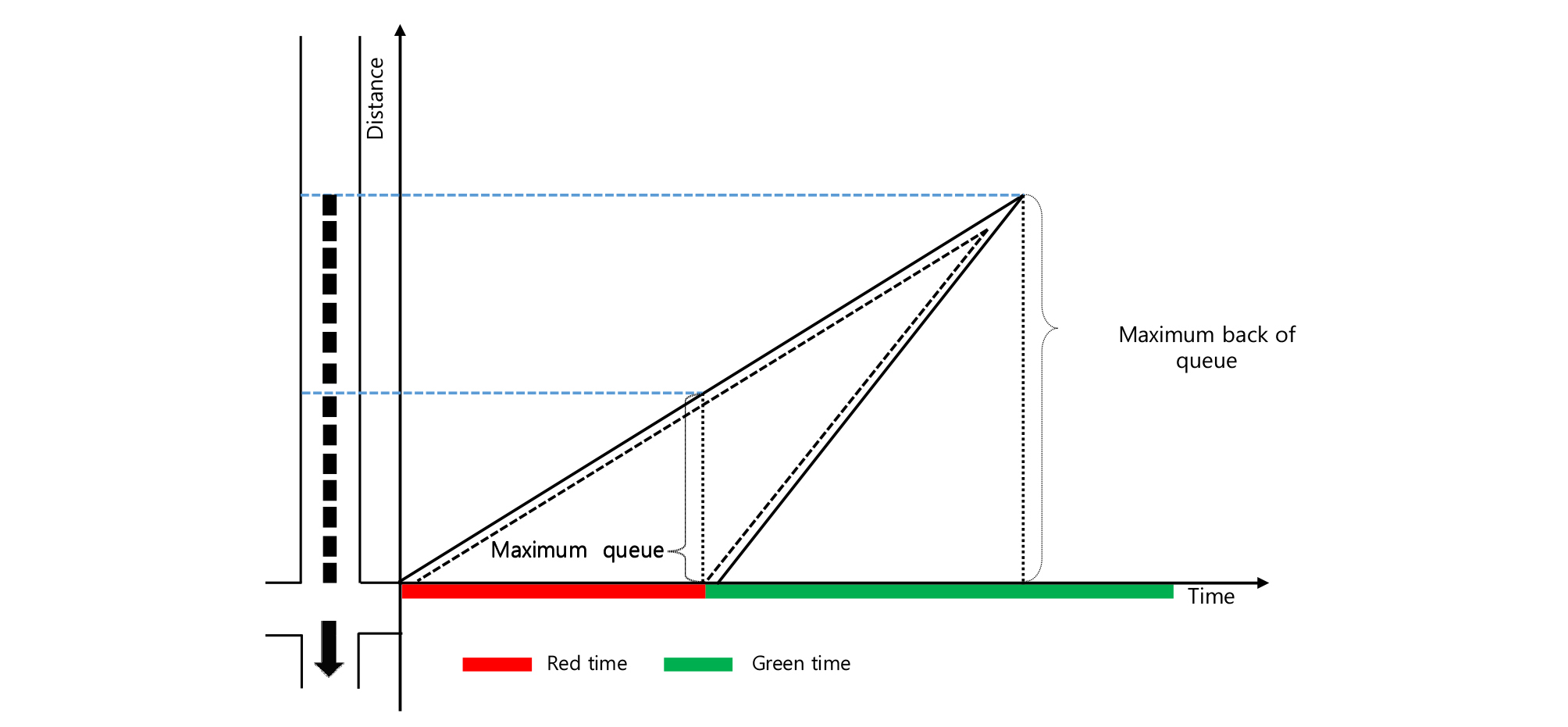
신호교차로에서 대기행렬은 하나의 주기 내에서 적색신호 및 녹색신호의 반복에 따라 생성되고 소멸되며, 정지선 뒤로 생성 된 대기행렬길이는 Figure 2와 같이 최대 대기행렬(Maximum queue) 및 후방 최대 대기행렬(Maximum back of queue)로 표현 될 수 있다. 최대 대기행렬은 주기 내에서 적색신호 시간동안 정지선 뒤로 생성된 차량의 대기행렬만을 의미하지만 후방 최대 대기행렬은 주기 내에서 정지대기행렬 및 정지대기행렬에 의해 생성되는 이동대기행렬을 모두 포함하므로 대기행렬 길이의 공간적인 범위를 나타내는데 더 적합하다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F2.jpg

Figure 2.

Definition of queue length at signalized intersections

3. 대기행렬 길이 추정

신호교차로에서 대기행렬 길이를 추정하기 위해 누적차량 모형(Cumulative Arrival and Departure Model)(Newell, 1960; Robertson, 1969; Akcelik, 2001; Sharma et al., 2007) 및 충격파 모형(Shockwave Model)(Lighthill and Whitham et al., 1955; Richards, 1956; Stephanopoulos et al., 1979)이 널리 사용된다. 누적차량 모형은 정지선에 순차적으로 도착하는 차량의 누적 곡선과 녹색시간 동안 정지선으로부터 출발하는 차량의 누적 곡선을 통해 특정 시점에 대기행렬을 이루고 있는 차량의 대수를 산정할 수 있으며, Lighthill and Whitham(1955)이 제시 한 충격파 모형은 도로의 모든 지점의 밀도관계를 기반으로 하는 함수로서 빠른 밀도 변화에 따른 전파운동으로 정의된다(May, 1990).

앞서 정의한 대기행렬 길이는 정지하고 있는 차량뿐만 아니라 일정 수준 이하의 속도 변화를 경험한 차량을 모두 포함하므로 대기행렬이 영향을 미치는 범위는 도착하는 차량의 속도변화에 따라서 상류로 이동 될 수 있다. 따라서 누적차량 모형의 경우 각 차량이 정지선을 기준으로 도착 및 출발하는 것을 가정하고 대기행렬 길이를 산정하므로 대기행렬이 영향을 미치는 공간적 범위를 추정하는데 한계가 있다.

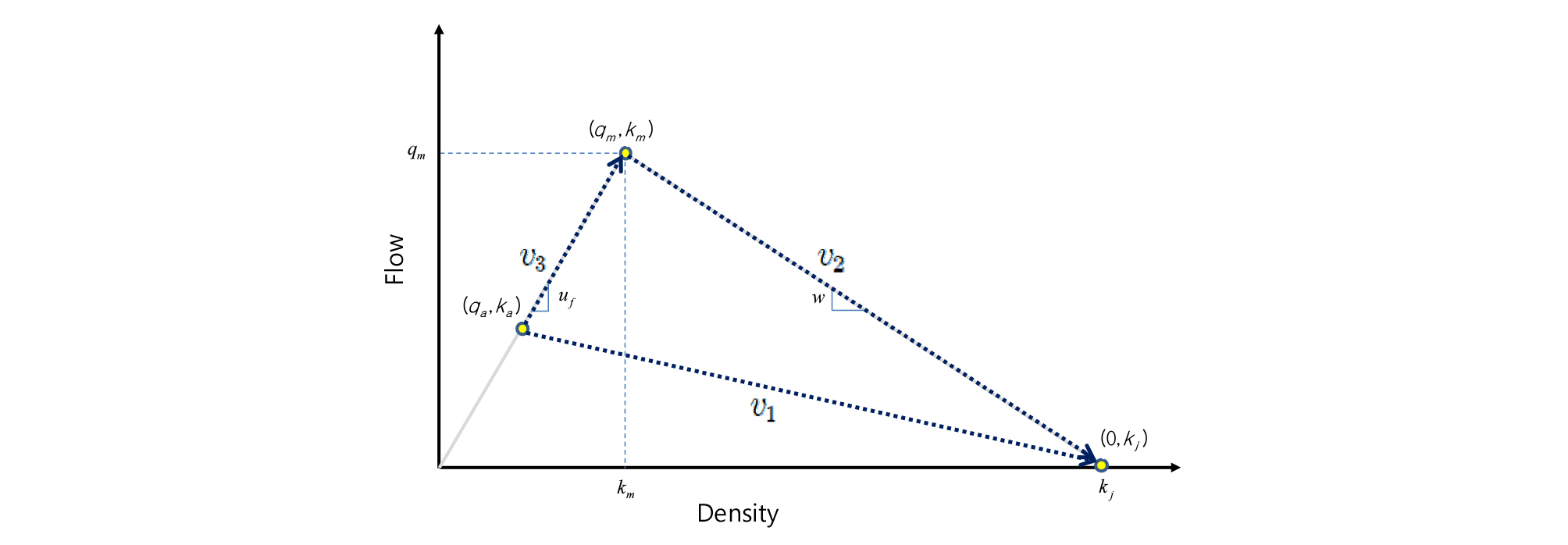
신호교차로에서 발생하는 충격파는 Figure 3과 같이 교통량-밀도 관계에 의해 3가지 충격파로 구분 될 수 있으며, Figure 1과 같이 시공도상에 나타낼 수 있다. 첫째, $v_{1}$ 은 적색 시간동안 정지선 후방으로 차량이 정지하면서 생성되는 대기행렬을 나타내는 충격파의 속도를 의미하며, 충격파의 속도는 도착하는 차량의 교통량에 따라 달라진다. 둘째, $v_{2}$ 는 녹색시간의 시작과 함께 대기행렬에서 차례대로 차량이 가속하여 이탈함으로서 생성되는 충격파의 속도를 나타낸다. 셋째, 일반적으로 정지선 후방으로 생성 된 두 개의 충격파 중 $v_{2}$ 의 속도가 $v_{1}$ 의 속도보다 빠르다. 따라서 두 개의 충격파는 후방 최대 대기행렬이 생성되는 지점에서 만나게 되며 새로운 충격파 $v_{3}$ 이 정지선 방향으로 생성되게 된다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F3.jpg

Figure 3.

Shockwaves at signalized intersections

충격파 모형을 활용한 이전 연구는 대기행렬이 생성되는 충격파의 속도( $v_{1}$ )를 추정하는데 사용된 장비 및 자료의 종류에 따라 다양한 방법이 연구되었다. 특정 지점에 설치된 루프 검지기를 활용한 방법의 경우 충격파의 속도를 추정하기 위해 검지기가 대기행렬에 의해 완전히 점유되기 이전의 자료들의 특성을 분석하여 대기행렬길이를 추정하는데 사용한다(Liu et al., 2009; Lertworawanich, 2011). GPS와 같은 모바일센서를 사용하는 연구의 경우 개별 차량의 속도변화를 감지할 수 있어 개별 차량이 대기행렬에 의해 속도의 변화가 발생하는 시점 및 지점을 활용하여 충격파를 속도를 추정한다(Cheng et al., 2011; Cetin, 2012). 각 차량의 통행시간을 사용하는 방법은 신호교차로의 상류와 하류에 사전 정의된 가상지점 또는 장비를 통해 수집된 통행시간을 활용하여 충격파의 속도를 추정한다(Ban et al., 2011; Wu and Yang, 2013).

알고리즘 개발

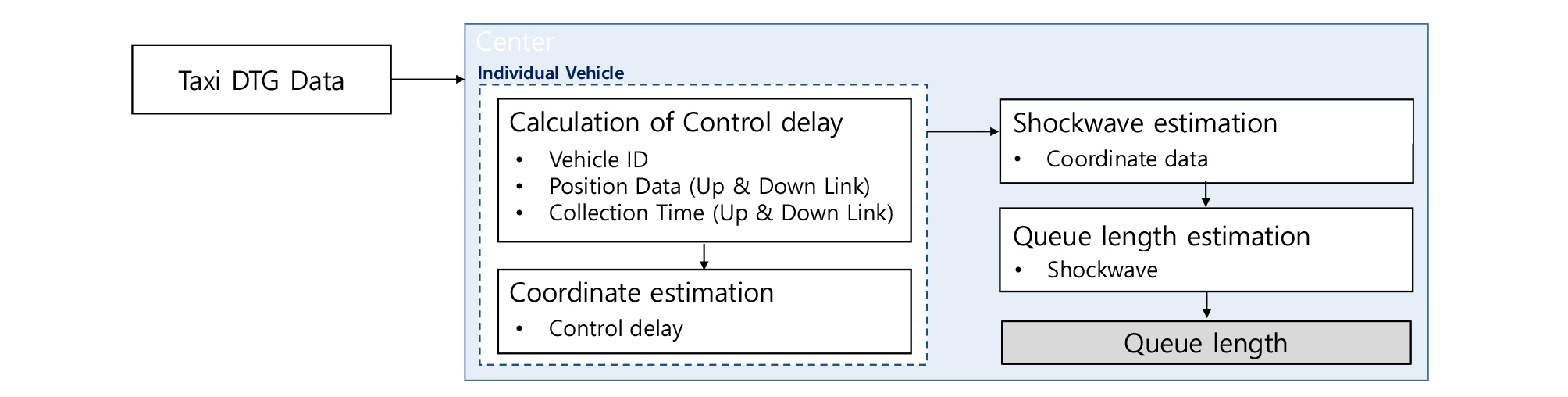
택시 DTG 자료를 활용한 대기행렬 길이 추정 알고리즘은 Figure 4와 같이 신호교차로를 통과한 개별 차량의 정보를 활용하여 개별 차량이 신호교차로를 통과하는데 소요된 통행시간을 추정하고 주기마다 추정된 개별 차량들의 통행시간 정보를 활용하여 대기행렬 길이를 추정한다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F4.jpg

Figure 4.

Algorithm procedure

1. 개별 차량의 제어지체 추정

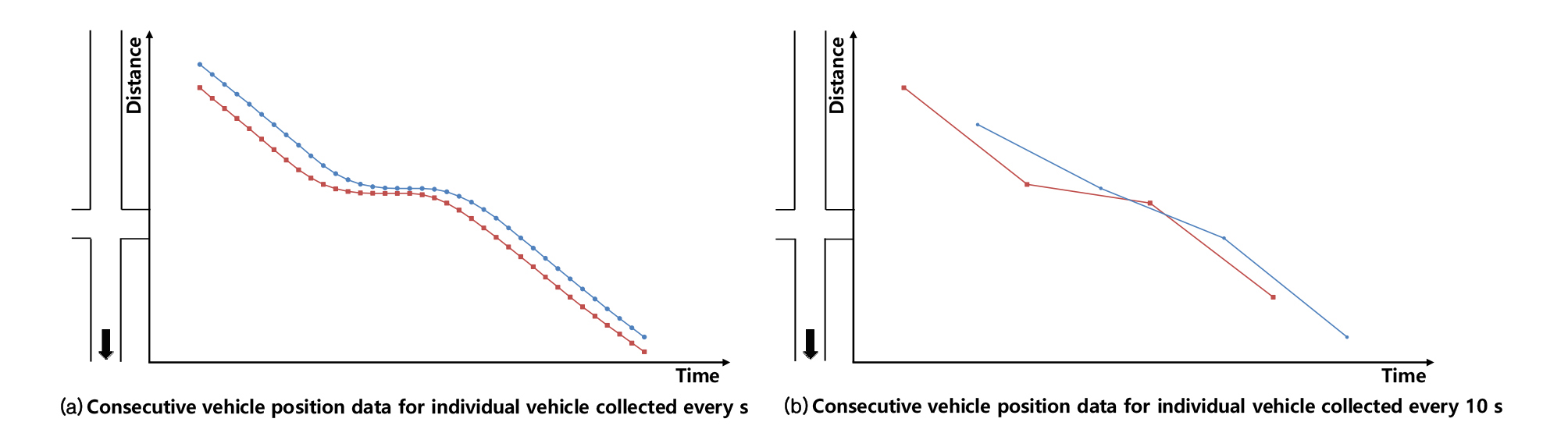
현재 서울시에서 수집되는 택시 DTG 자료는 10초마다 수집된 개별 택시의 위치, 속도 및 수집시각 등을 150초마다 교통정보센터(TOPIS)로 전송하며, 교통정보센터에서는 수집된 원시 자료를 3단계의 처리과정을 거쳐 도시 전체의 실시간 교통정보를 생성한다(Han and Kim, 2017). 따라서 DTG를 통해 수집되는 개별 택시의 위치정보를 활용하기 위해서는 DTG의 정보수집 및 수집된 정보를 전송하는 시간간격에 대한 제약 사항이 고려되어야한다. Figure 5는 동일한 차량에서 정보수집 간격을 달리하여 수집된 차량의 주행궤적이다. (a)의 경우 두 개의 연속된 차량의 가 ‧ 감속 또는 정지 위치를 확인 할 수 있으나 (b)의 경우 개별 차량의 속도 변화에 대한 명확한 정보를 확인할 수 없다. 하지만 신호교차로를 포함하는 사전 정의된 구간의 통행시간은 위치정보의 수집시간 간격과 관계없이 신호제어에 의해 발생하는 제어지체를 동일하게 포함하게 된다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F5.jpg

Figure 5.

Trajectory of vehicle according to collection time

택시 DTG 자료의 경우에도 신호교차로를 기준으로 상류 링크와 하류 링크에서 수집 된 개별 택시의 수집시각 차이에 신호제어로 인해 발생되는 제어지체를 포함한다. 따라서 본 논문에서는 상류와 하류 링크에서 처음으로 수집 된 개별 택시의 수집시각을 활용하여 제어지체를 포함한 개별 차량의 통행시간을 Equation 1을 통해 산정한다.

$$t_{TT,i}=t_{D,i}-t_{U,i}$$

(1)

여기서, $t_{T T, i}$ :차량 $i$ 의 통행시간
$t_{U, i}$ : 차량 $i$ 가 상류 링크에서 처음 수집된 시각
$t_{D, i}$ : 차량 $i$ 가 하류 링크에서 처음 수집된 시각

개별 차량의 제어지체는 산정된 통행시간에 자유속도로 이동하는데 소요되는 시간을 감하는 Equation 2를 통해 산정한다.

$$Delay_i=t_{TT,i}-\frac{L_i}{v_f}$$

(2)

여기서, $D e l a y_{i}$ :차량 $i$ 의 제어지체
$L_{i}$ : 차량 $i$ 가 상류 링크와 하류 링크에서 처음 수집된 지점의 거리차이
$v_{f}$ : 자유속도

2. 개별 차량의 좌표 추정

Figure 1은 시공도에서 신호교차로를 통과하는 개별 차량들의 주행궤적을 나타낸 것으로 신호등화의 변화에 따라 개별 차량들의 속도변화를 확인할 수 있다. 이러한 속도변화는 발생시점 및 지점을 기준으로 상류부와 하류부의 밀도변화가 동반되며 연속된 개별 차량의 속도변화가 발생하는 지점을 연결한 경계선의 기울기를 통해 신호교차로에서 대기행렬이 생성 및 소멸되며 발생되는 충격파를 추정할 수 있다.

본 논문에서는 택시 DTG 자료를 통해 추정된 개별 차량의 통행시간을 활용하여 Figure 6과 같이 시공도에서 4개의 개별 차량의 좌표를 추정하며, 추정된 좌표를 활용하여 충격파의 속도를 결정한다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F6.jpg

Figure 6.

Coordinates of an individual vehicle on the time-space diagram

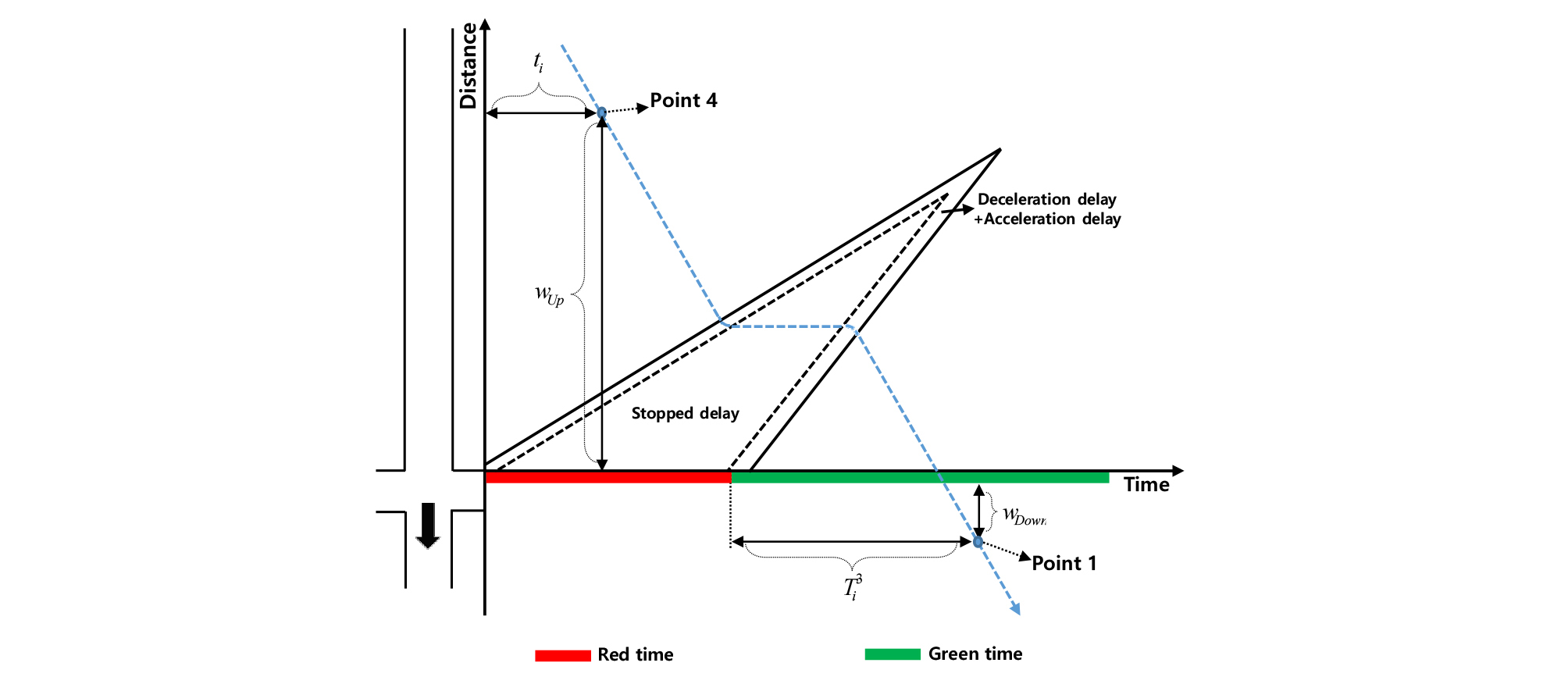
Figure 7의 $P o i n t 1$ 과 $P o i n t 4$ 좌표는 상류 및 하류 링크에서 처음으로 수집된 개별 차량의 위치 및 시간을 의미하며, Equation 3과 Equation 4로 표현될 수 있다.

$$Point1=(Redtime+T_i^3,\;w_{Down,i})$$

(3)

$$Point4=(t_{U,i}-Redtime_s,\;w_{Down,i})$$

(4)

여기서, $T_{i}^{3}$ :녹색시간 시작 이후 개별 차량이 하류부 링크에서 처음 정보를 수집하는 시각
$w_{U p, i}$ : 정지선과 상류뷰 링크에서 차량 $i$ 의 정보가 처음 수집된 지점의 거리차이
$w_{D o w n, i}$ : 정지선과 하류뷰 링크에서 차량 $i$ 의 정보가 처음 수집된 지점의 거리차이
$R e d t i m e_{s}$ : 해당현시 적색신호가 시작하는 시각

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F7.jpg

Figure 7.

Estimation of coordinates of Point 1 and Point 4 on the time-space diagram

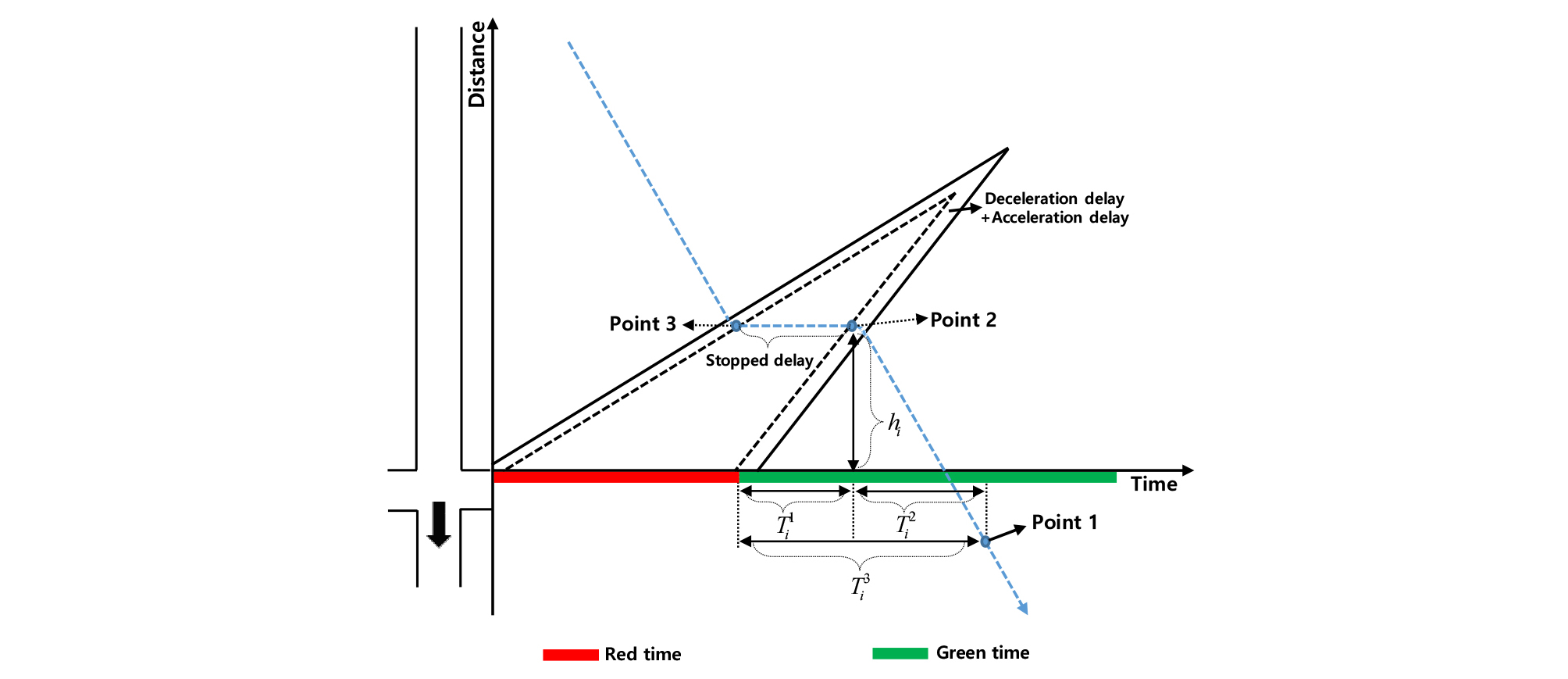
Figure 8의 $P o i n t 2$ 와 $P o i n t 3$ 은 개별 차량의 속도 변화가 발생하는 지점 및 시점으로 충격파상에 위치한 개별 차량의 좌표를 의미한다. $P o i n t 2$ 는 적색시간 동안 생성된 대기행렬에서 녹색시간의 시작과 함께 차량들이 대기행렬을 이탈하며 발생되는 충격파상에 위치한다. 정지선 후방으로 생성되는 충격파 $S h o c k w a v e_{2}$ 의 속도는 교통량-밀도 관계에서 임계밀도(Critical density)와 혼잡밀도(Jam density)의 기울기로 나타낼 수 있다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F8.jpg

Figure 8.

Estimation of coordinates of Point 2 and Point 3 on the time-space diagram

녹색시간 시작 이후 개별 차량이 하류부 링크에서 처음 정보를 수집하는 시각을 나타내는 $T_{i}^{3}$ 는 $T_{i}^{1}$ 과 $T_{i}^{2}$ 의 합으로 나타낼 수 있다. $T_{i}^{1}$ 은 녹색시간의 시작 이후 정지하고 있는 개별 차량의 속도가 증가하는 시점으로 $S h o c k w a v e_{2}$ 가 대기행렬에 속한 개별 차량의 위치에 도달하는 시간을 의미한다. $T_{i}^{2}$ 는 개별 차량이 대기행렬을 이탈하여 정지선을 통과한 이후 하류부 링크에서 처음으로 정보가 수집되기까지 소요되는 시간간격을 의미하며, 이는 개별 차량이 자유속도를 회복하는데 소요되는 시간과 이후 자유속도로 하류부 링크에서 정보가 수집되기까지 주행한 시간의 합으로 나타낼 수 있다.

정지선에서 대기행렬에 속한 개별 차량까지의 거리를 나타내는 $h_{i}$ 는 Equation 5로 나타낼 수 있으며, $P o i n t 2$ 의 위치좌표를 의미한다.

$$h_i=Shockwave_{{}_2}\times T_i^1$$

(5)

여기서, $h_{i}$ : 정지선에서 대기행렬에 속한 개별 차량까지의 거리
$S h o c k w a v e_{_{2}}$ : 대기행렬을 이탕하는 차량에 의해 정지선 후방으로 생성되는 충격파의 속도

$T_{i}^{2}$ 동안 개별 차량이 이동 한 거리는 $h_{i}$ 와 $w_{D o w n, i}$ 의 합으로 Equation 6과 같으며, 개별 차량이 자유속도를 회복하는데 소요되는 시간에 개별 차량의 가속지체가 포함된다.

$$h_i+w_{Down,i}=t_{re}+\frac12at_f^2+v_f(T_i^2-t_f)$$

(6)

여기서, $t_{r e}$ : 인지반응시간
$t_{f}$ : 대기행렬에 속한 개별 차량이 자유속도를 회복하는데 필요한 시간

$T_{i}^{2}$ 는 Equation 7로 나타낼 수 있으며, $T_{i}^{1}$ 은 $T_{i}^{3}$ 와 $T_{i}^{2}$ 의 차로 산정될 수 있다.

$$T_i^2=\frac{Shockwave_2\times T_i^3-(\frac12at_f^2)+v_f\times t_f-t_{re}+w_{Down,i}}{Shockwave_2+v_f}$$

(7)

$P o i n t 2$ 는 Equation 8과 같으며 $P o i n t 3$ 는 $P o i n t 2$ 의 시간좌표에 개별 차량의 정지지체(Stopped delay)를 감한 Equation 9로 나타낼 수 있다.

$$Point2=(Redtiem+T_i^1,\;h_i)$$

(8)

$$Point3=(Redtime+T_i^1-(delay_i-(AccDelay+DecdDelay)),h_i)$$

(9)

여기서, $T_{i}^{1}$ : $S h o c k w a v e_{2}$ 가 차량 $i$ 에 도착하는 시각
$A c c D e l a y$ : 개별 차량의 가속지체
$D e c d D e l a y$ : 개별 차량의 감속지체

3. 충격파 추정 및 대기행렬 길이 산정

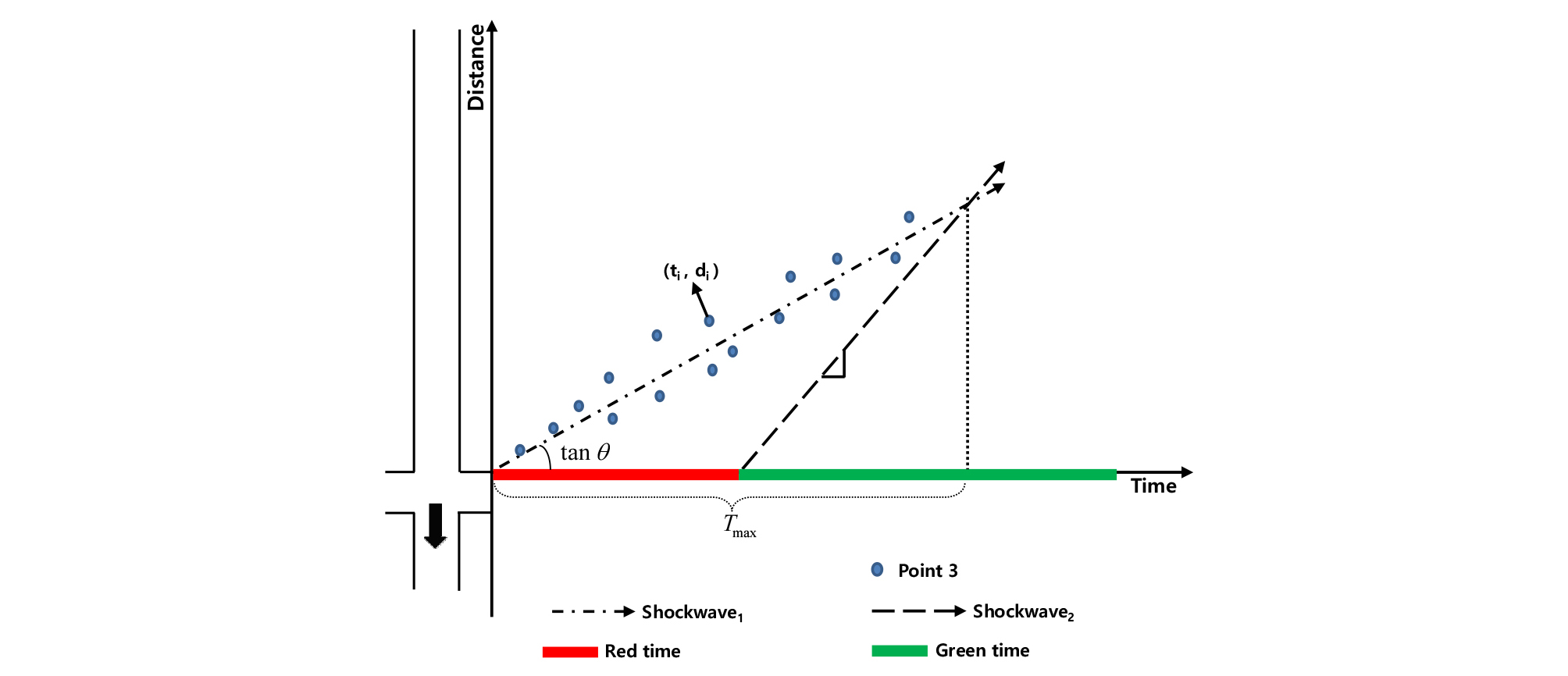
$S h o c k w a v e_{1}$ 은 대기행렬이 정지선 후방으로 생성될 때 발생하는 충격파의 속도로서 시공도상의 기울기는 접근로의 수요를 대변한다. 본 연구에서는 한 주기 동안 수집된 개별 차량의 $P o i n t 3$ 좌표를 활용하여 충격파의 속도를 추정하기 위해 최소제곱법을 사용하였다.

최소제곱법은 측정값과 함수값의 차를 제곱한 것의 총합이 최소가 되는 함수를 찾는 것으로 시공도에서 정지선과 해당 주기의 시작시점을 원점으로 가정 할 경우 $S h o c k w a v e_{1}$ 의 속도는 항상 양의 값을 가지게 된다. 따라서 원점을 지나는 일차방정식과 $P o i n t 3$ 좌표와의 거리가 최소가 되는 일차방정식의 기울기( $\tan θ$ )는 Equation 10을 통해 산정할 수 있다.

$$\begin{array}{l}Find\tan\theta\\\\Minimize\sum_{i=1}^n\frac{\left|t_i\times\tan\theta-d_i\right|}{\sqrt{\tan^2\theta+1}}\end{array}$$

(10)

여기서, $\tan θ$ : $S h o c k w a v e_{1}$ 의 속도
$t_{i}$ : 차량 $i$ 의 $P o i n t 3$ 의 X좌표
$d_{i}$ : 차량 $i$ 의 $P o i n t 3$ 의 Y좌표

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F9.jpg

Figure 9.

Estimation of shockwave

$S h o c k w a v e_{1}$ 의 속도를 활용하여 산정된 대기행렬 길이는 $S h o c k w a v e_{1}$ 과 $S h o c k w a v e_{2}$ 가 만나는 시점까지 대기행렬이 정지선 후방으로 영향을 미치는 범위를 나타내며 Equation 11을 통해 산정될 수 있다.

$$QueueLength_1=\tan\theta\times t_\max$$

(11)

여기서, $t_{\max}$ : $S h o c k w a v e_{1}$ 와 $S h o c k w a v e_{2}$ 가 만나는 시각

4. 도착률 변화를 고려한 대기행렬 길이 산정

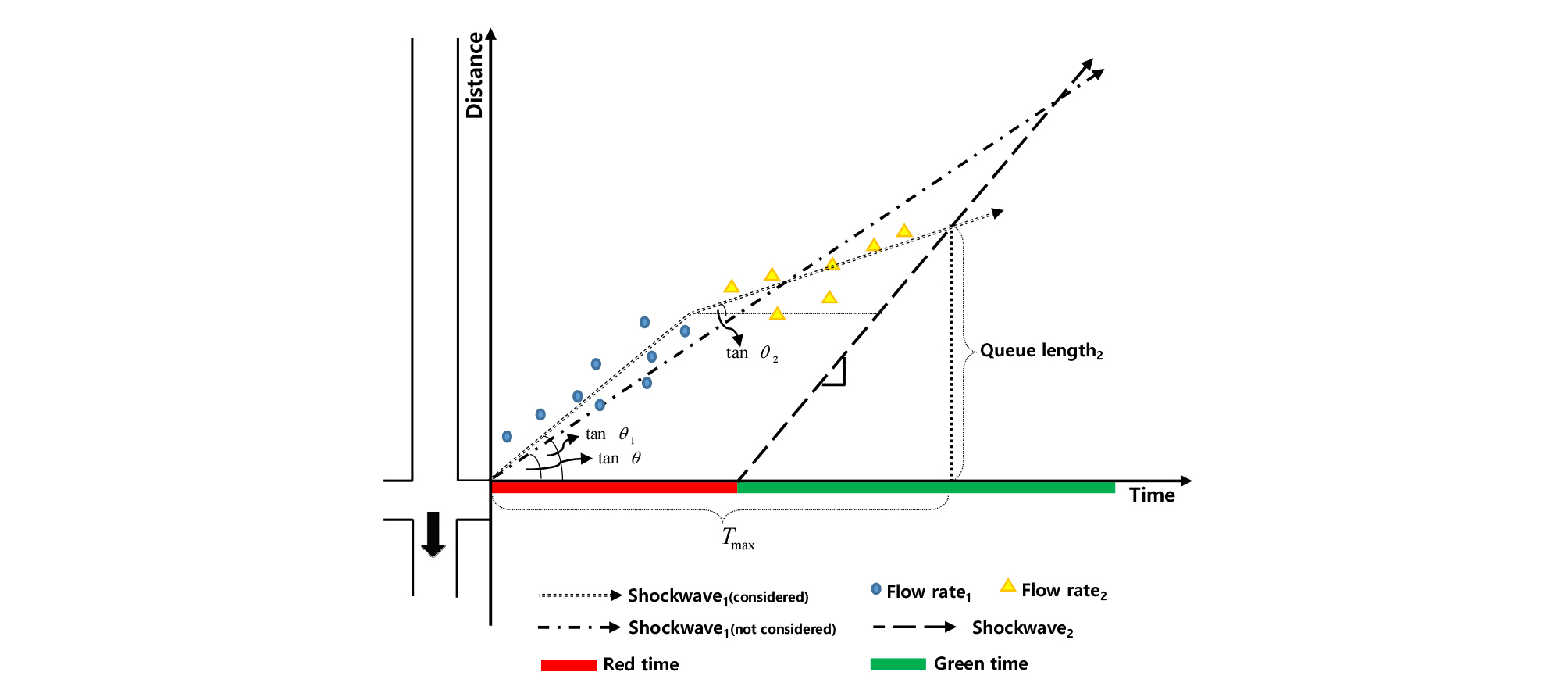
교차로에 도착하는 차량군의 밀도는 상류 교차로의 직진과 좌회전 신호시간 및 각 신호시간에 통과하는 교통량의 차이에 의해 항상 일정하지 않다. 따라서 Figure 10과 같이 접근로의 차량군의 밀도변화에 따라 충격파의 기울기가 변하는 시점이 발생하게 된다. 따라서 충격파의 속도 변화는 대기행렬 길이에 영향을 미치게 되므로 차량군의 밀도 변화를 고려한 대기행렬 길이의 산정이 요구된다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F10.jpg

Figure 10.

Estimation of queue length considering change in arrival rate

Equation 12는 차량군의 밀도 변화를 고려하여 2개의 충격파의 속도를 추정할 수 있으며, Equation 13을 통해 대기행렬의 길이를 산정할 수 있다.

$$\begin{array}{l}Find\tan\theta_1,\tan\theta_2\\\\Minimize\sum_{i=1}^n\frac{\left|t_i\times\tan\theta_1-d_i\right|}{\sqrt{\tan^2\theta_1+1}}+\sum_{i=1}^n\frac{\left|(t_i-t_o)\times\tan\theta_2-(d_i-\tan\theta_1\times t_o)\right|}{\sqrt{\tan^2\theta_2+1}}\end{array}$$

(12)

$$QueueLength_2=\tan\theta_1\times t_o+\tan\theta_2\times(t_{\max-}t_o)$$

(13)

여기서, $t_{o}$ : 접근로의 도착률 변화가 발생하는 시각
$\tan θ_{1}$ : 차량군 1의 충격파 속도
$\tan θ_{2}$ : 차량군 2의 충격파 속도

알고리즘 모의실험

1. 모의실험 환경구축

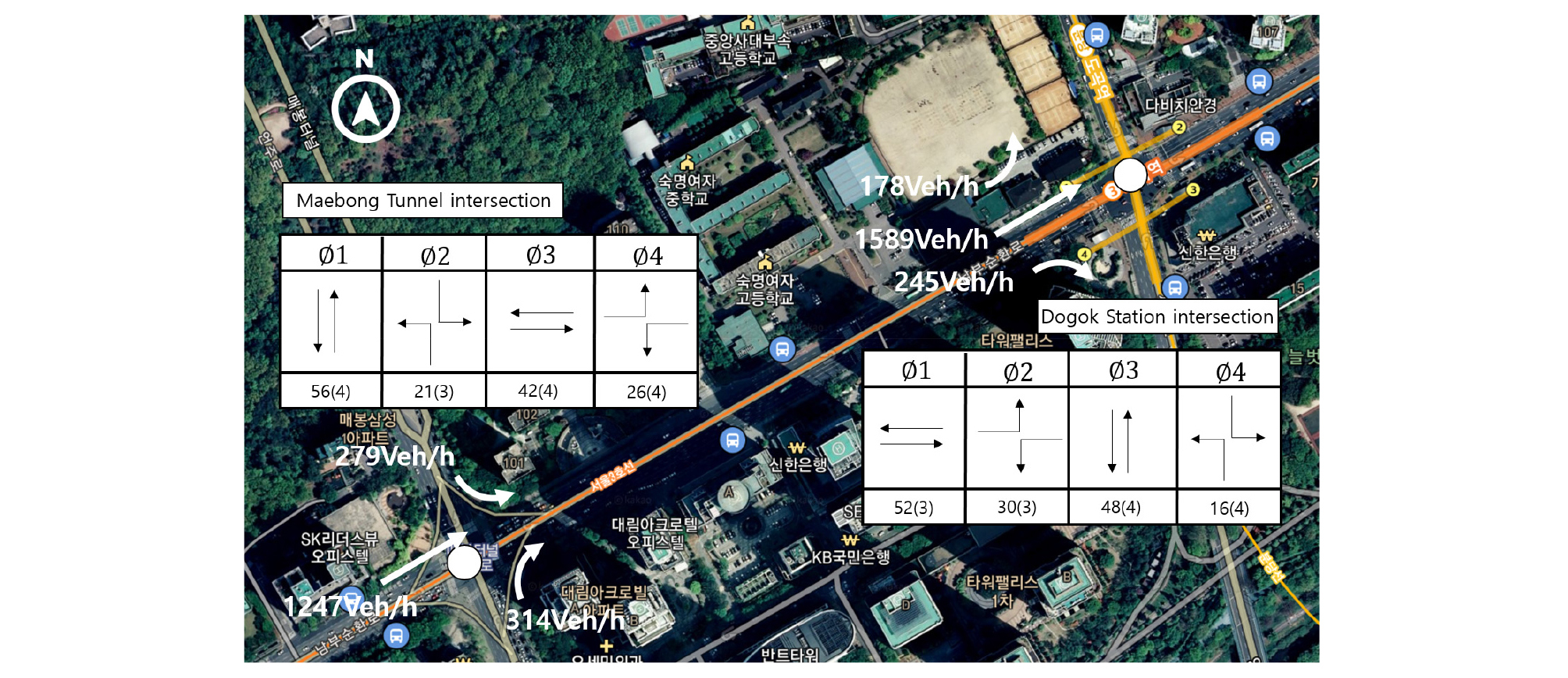
제안 된 알고리즘은 마이크로시뮬레이션 소프트웨어인 VISSIM을 활용하여 평가하였다. 모의실험대상지역은 서울특별시 강남구에 위치한 도곡역교차로의 동향 접근로의 직진현시를 대상으로 하였다. 상류교차로인 매봉터널교차로와 도곡역교차로의 거리는 553m이며 교통량 및 신호시간은 Figure 11과 같다. 분석대상 현시는 상류부 교차로에서 진입하는 직진과 좌회전 차량군의 교통량 수준이 상이하여 대기행렬 생성속도의 변화가 발생하므로 도착률의 변화를 고려한 대기행렬 길이 산정방안을 적용하였다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F11.jpg

Figure 11.

Simulation study area and traffic environment

개별 차량의 가속도 및 감속도는 3.5m/s²로 가정하였으며 속도가 5km/h 미만인 경우 개별 차량이 대기행렬에 속하는 것으로 가정하였다. 프로브차량의 비율은 시뮬레이션의 차종구성에서 DTG 자료를 수집 할 수 있는 택시를 구분하여 현장에서 조사된 택시의 비율인 10%로 설정하였으며, 1회 3600초의 시뮬레이션 수행시간을 기반으로 6번의 시드넘버 변경을 통해 총 132회의 대기행렬 길이를 추정하였다. 또한 프로브차량의 비율에 따른 알고리즘의 민감도를 분석하기 위해 택시의 비율을 달리하여 분석을 수행하였다.

2. 모의실험 결과분석

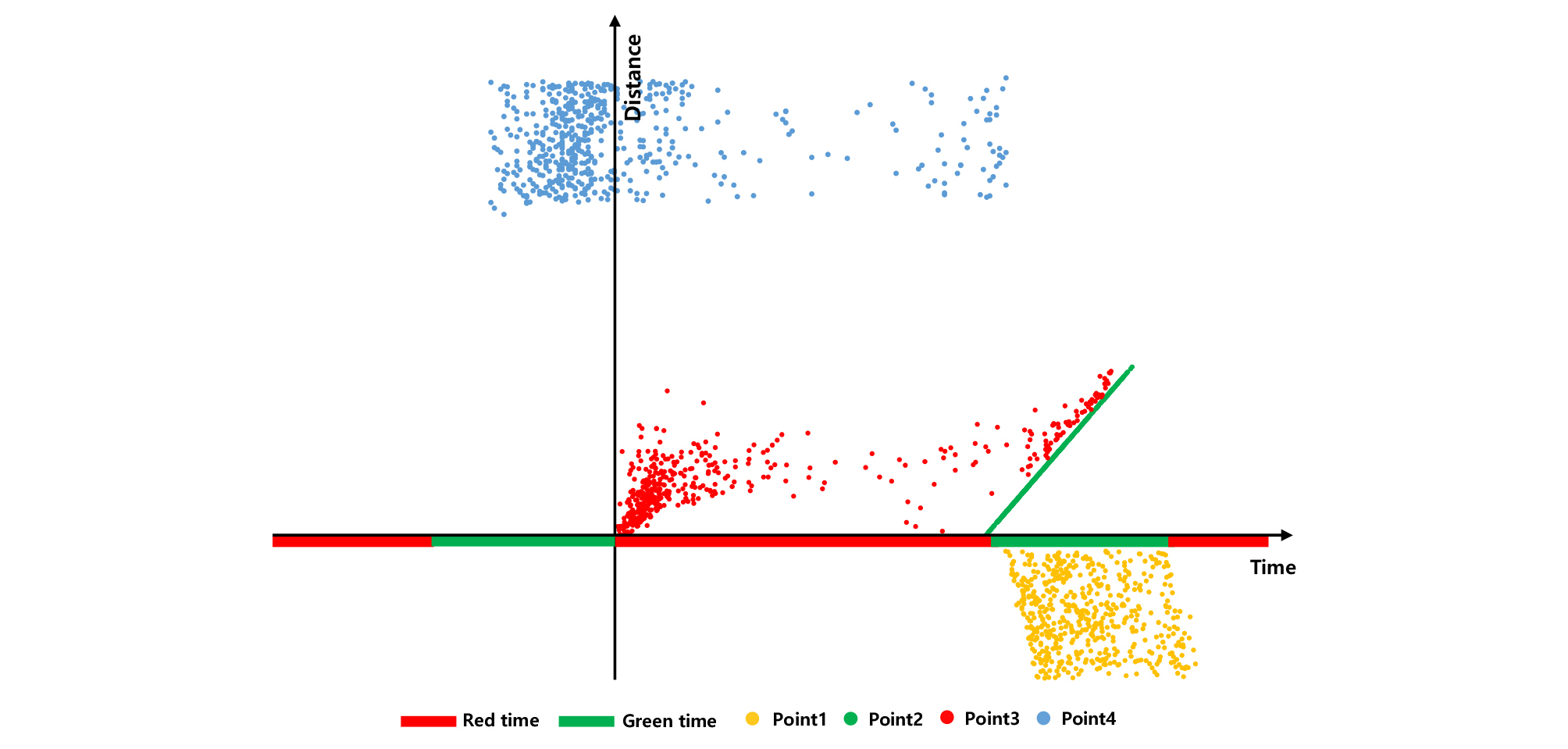
시뮬레이션을 통해 추정 된 개별 차량의 위치좌표는 Figure 12와 같다. 개별 차량이 링크에서 처음으로 수집된 시간 및 위치를 나타내는 $P o i n t 1$ 과 $P o i n t 4$ 는 차량 별로 10초 간격으로 수집되는 택시 DTG 자료의 특성에 따라 공간적으로 넓게 분포되어 있는 것을 알 수 있으며 수집된 $P o i n t 1$ 과 $P o i n t 4$ 의 좌표를 통해 개별 차량이 신호제어에 의해 속도 변화가 발생하는 $P o i n t 2$ 과 $P o i n t 3$ 의 좌표의 추정이 가능함으로서 10초마다 위치 및 시간을 수집하는 택시 DTG 자료의 단점을 극복할 수 있음을 보여준다. 또한 대기행렬 길이와 관련된 $S h o c k w a v e_{1}$ 에 위치한 $P o i n t 2$ 의 좌표들이 밀도 변화에 따라 기울기의 변화가 발생하여 차량군의 밀도 변화를 고려한 대기행렬 길이의 산정이 필요함을 알 수 있다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F12.jpg

Figure 12.

Estimated coordinates of individual vehicles

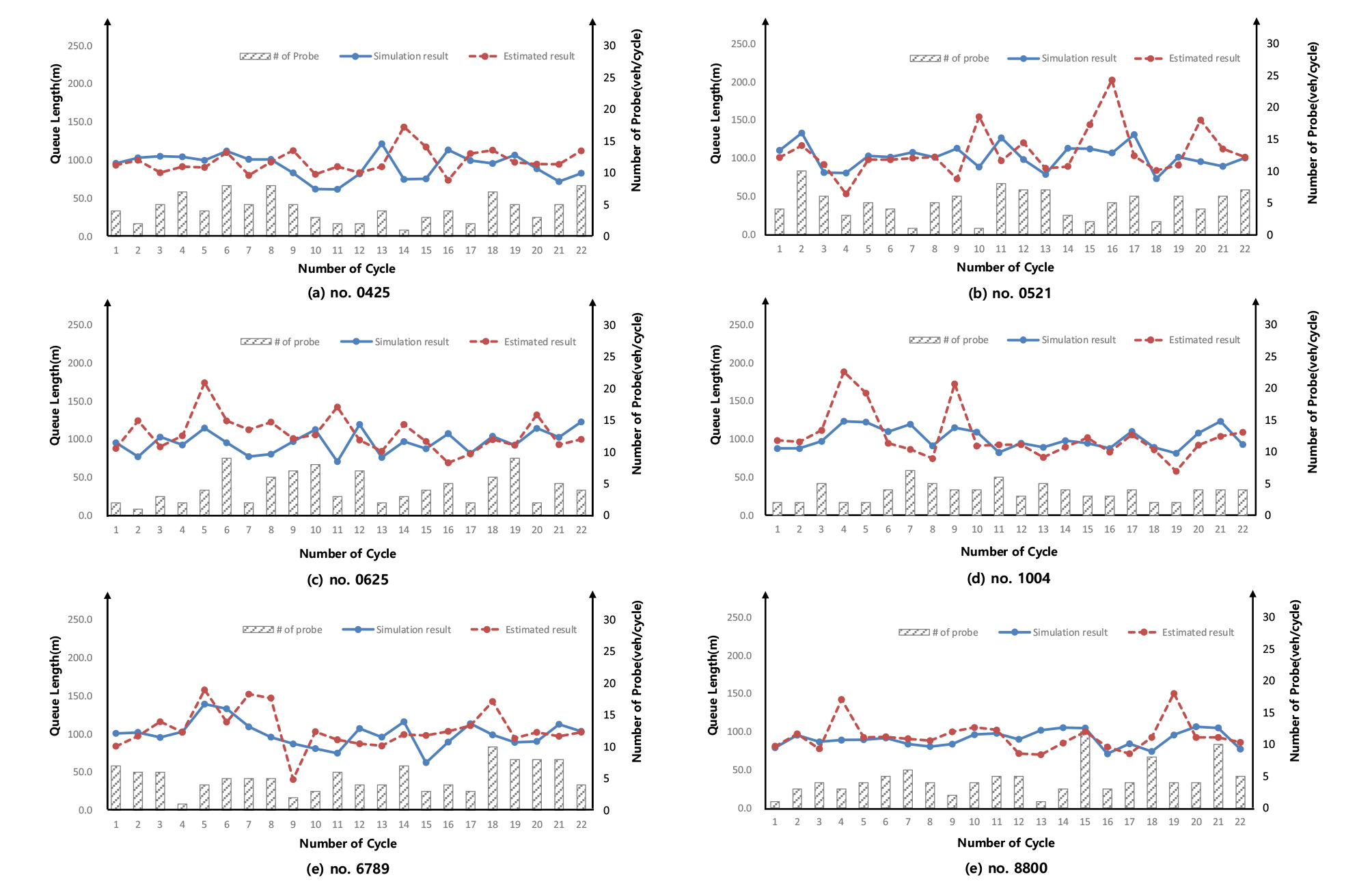
시드넘버에 따른 대기행렬 길이의 시뮬레이션 실측값과 알고리즘 추정값은 Figure 13과 같다. 총 132회의 대기행렬 길이 추정값에 대한 평균절대비율오차(Mean Absolute Percentage Error, MAPE)는 19.8%로서 매초단위 GPS를 기반으로 수집된 개별 차량의 궤적정보를 활용한 Cheng et al.(2011)의 연구결과 평균절대비율오차가 20.6%로 제시된 것과 비교할 때 제안 된 알고리즘을 통해 시드넘버 및 주기 변화에 따른 교통량 변동을 반영한 대기행렬 길이의 추정이 가능함을 알 수 있다. 하지만 일부 추정값의 경우 수집된 프로브차량의 수가 적어 모든 차량군의 도착률이 고려되지 않거나 수집된 프로브차량이 특정 차량군에만 치중되어 특정 차량군 수요만을 반영한 대기행렬 길이를 산출하므로서 대기행렬 길이가 과대 또는 과소 추정되었다. 또한 수집된 위치 및 시각을 2분 30초 단위로 DTG에서 전송함으로서 상류부에서 수집된 정보와 하류부에서 수집된 정보를 전송하는 시점이 상이할 경우 추정을 위해 활용되는 차량 좌표가 생성되는데 5분 이상이 소요되어 해당 차량이 통과한 주기가 아닌 다음 주기의 분석에 활용되어 대기행렬 길이의 변화가 큰 경우 추정의 오차를 발생시키는 원인이 되었다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F13.jpg

Figure 13.

Comparison of results of each seed number

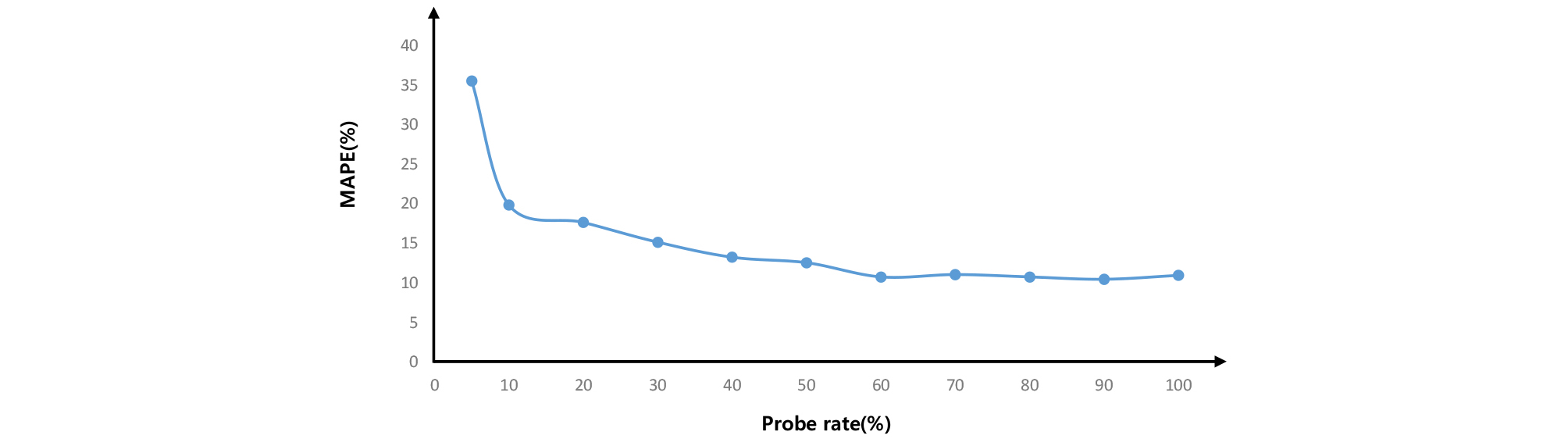
제안된 알고리즘은 10초 단위로 개별 차량의 위치정보가 수집되는 단점을 극복하기 위해 분석 대상 교차로를 기준으로 상류 및 하류링크에서 개별 차량이 최초로 검지된 시점을 기반으로 산출된 통행시간을 활용하였다. 하지만 프로브차량 정보에 기반하는 알고리즘의 특성상 수집된 프로브차량의 수가 알고리즘의 정확도 영향을 미치게 되므로 프로브차량의 비율에 따른 알고리즘의 민감도를 분석하였다. 프로브차량의 비율에 따른 알고리즘의 민감도 분석결과 Figure 14와 같이 프로브차량 비율이 10% 이하인 경우 평균절대비율오차가 크게 증가하는 반면 프로브차량 비율이 50% 이상인 경우에는 약 10%수준으로 프로브차량의 비율에 관계없이 유사한 평균절대비율오차를 보였다. 이는 앞서 언급한 것과 같이 Figure 13에서 프로브차량이 10%인 경우 주기 당 평균 5대의 프로브차량이 수집되었으나 특정 주기의 경우 1-2대 수준의 프로브차량이 수집됨으로서 모든 차량군의 도착률이 고려되지 않아 추정값의 오차가 크게 발생하였다. 따라서 프로브차량의 비율이 5% 이하일 경우 매주기 수집된 프로브차량의 수는 평균 3대로서 추정값의 오차가 크게 발생하는 주기의 비율이 증가하며 평균절대비율오차의 값이 크게 증가하였다. 또한 프로브차량의 비율이 50% 이상인 경우 매주기 평균 25대의 차량이 수집됨으로서 프로브차량의 수가 증가하더라도 알고리즘의 정확도에 영향을 미치지 못하는 것을 알 수 있다.

http://static.apub.kr/journalsite/sites/kst/2020-038-01/N0210380106/images/kst_38_01_06_F14.jpg

Figure 14.

MAPE of queue length estimation with variation in probe rate

결론

본 연구는 택시 DTG 자료를 활용하여 신호교차로에서 대기행렬 길이를 추정하는 알고리즘을 제안하였다. 알고리즘은 10초 단위로 정보를 수집하는 택시 DTG 자료의 특성을 고려하여 신호교차로의 상류 링크 및 하류 링크에서 수집된 정보를 활용하여 개별 차량의 제어지체 및 속도변화가 발생하는 지점 및 시점을 추정하였다. 이렇게 산정된 개별 차량의 좌표 중 차량의 속도가 감소하는 지점의 좌표들을 활용하여 접근로의 도착수요를 나타내는 충격파의 속도를 추정하였으며 밀도의 변화가 발생하는 경우 밀도변화를 고려하여 충격파의 속도변화를 반영하였다. 알고리즘은 시뮬레이션을 통해 실측값과 추정값을 비교함으로서 택시 DTG 자료를 활용하여 신호교차로에서 대기행렬 길이를 추정 할 수 있음을 확인하였으며 택시의 비율을 달리하여 프로브차량의 비율에 따른 알고리즘의 민감도를 분석하였다. 분석결과 일부 추정값의 경우 프로브차량의 분포가 특정 차량군에 편중되어 도착차량의 밀도 변화가 고려되지 않아 대기행렬 길이가 과대 또는 과소 추정되었으며 이는 민감도 분석을 통해 추정값의 오차를 줄이기 위해 주기 당 최소 5대 이상의 프로브차량이 요구됨을 확인하였다.

본 연구에서는 개발 된 알고리즘의 정확성을 측정하기 위해 마이크로시뮬레이션 소프트웨어를 사용하였다. 하자만 현장자료의 경우 일반적인 GPS 오차 및 승객의 승하차와 같이 특정 운송수단이 가지는 특성이 반영되어 있다. 따라서 향후 연구에서는 개인정보 보호법의 개정에 따라 비식별화된 개별 차량의 현장자료를 활용한 알고리즘의 추가적인 검증 및 연구수행이 필요할 것으로 판단된다.

Funding

This research was supported by Projects for Research and Development of Police science and Technology under Center for Research and Development of Police science and Technology and Korean National Police Agency funded by the Ministry of Science, ICT and Future Planning (PA-A000001-2015-101).

알림

본 논문은 2019년도 한국ITS학회 춘계학술대회(2019.04.18)에서 발표된 내용을 수정 ‧ 보완하여 작성된 것입니다.

References

Akcelik R. (2001), HCM 2000 Back of Queue Model for Signalised Intersections, Technical Note, Akcelik and Associates Pty Ltd, Melbourne, Australia.

Ban X. J., Hao P., Sun Z. (2011), Real Time Queue Length Estimation for Signalized Intersections Using Travel Times from Mobile Sensors, Transportation Research Part C: Emerging Technologies, 19(6), 1133-1156.

10.1016/j.trc.2011.01.002

Cetin M. (2012), Estimating Queue Dynamics at Signalized Intersections from Probe Vehicle Data: A Methodology Based on Kinematic Wave Model, Transportation Research Record, 2315, 164-172.

10.3141/2315-17

Cheng Y., Qin X., Jin J., Ran B., Anderson J. (2011), Cycle-by-cycle Queue Length Estimation for Signalized Intersections Using Sampled Trajectory Data, Transportation Research Record, 2257, 87-94.

10.3141/2257-10

Federal Highway Administration (FHWA) (2007), Traffic Analysis Toolbox Volume VI: Definition, Interpretation, and Calculation of Traffic Analysis Tools Measures of Effectiveness, No. FHWA-HOP-08-054. US Department of Transportation, Washington, D.C.

Han Y., Kim Y. (2017), A Study of Measuring Traffic Congestion for Urban Network Using Average Link Travel Time Based on DTG Big Data, Journal of Korea Institute of Intelligent Transportation System, 16(5), 72-84.

10.12815/kits.2017.16.5.72

Jang Y., Jo S., Ahn S. (2015), Sustainable Traffic Information Private-government Sector Cooperative Policy Direction, Transportation Technology and Policy, 12(1), 83-92

Lertworawanich P. (2011), A Self-tuning Signal Control Algorithm for Isolated Intersections based on Time-space Diagrams, Proc. East. Asia Soc. Transportation Studies, 8, 1416-1431.

Lighthill M. J., Whitham G. B. (1955), On Kinematic Waves II, A theory of Traffic Flow on Long Crowded Roads, Proceedings of the Royal Society A, Mathematical, Physical and Engineering Sciences, 229(1178), 317-345.

10.1098/rspa.1955.0089

Liu H. X., Ma W., Wu X., Hu H. (2012), Real-time Estimation of Arterial Travel Time under Congested Conditions, Transportmetrica, 8(2), 87-104.

10.1080/18128600903502298

Liu H. X., Wu X., Ma W., Hu H. (2009), Real-time Queue Length Estimation for Congested Signalized Intersections, Transportation Research Part C: Emerging Technologies, 17(4), 412-427.

10.1016/j.trc.2009.02.003

May A. D. (1990), Traffic Flow Fundamentals, Prentice Hall, NJ, USA.

Ministry of Land, Infrastructure and Transport (MOLIT) (2017), 2017 Statistical Yearbook of Ministry of Land, Infrastructure and Transport, Republic of Korea.

Newell G. F. (1960), Queues for a fixed-cycle traffic light, The Annals of Mathematical Statistics, 31(3), 589-597.

10.1214/aoms/1177705787

Richards P. I. (1956), Shock waves on the highway, Operations Research, 4(1), 42-51.

10.1287/opre.4.1.42

Robertson D. I. (1969), TRANSYT : A Traffic Network Study Tool. Technical report 253, Transport Road Research Laboratory, UK.

Roess R. P., Prassas E. S., McShane W. R. (2011), Traffic Engineering, 4th Ed, Prentice Hall, NJ, USA.

Sharma A., Bullock D. M., Bonneson J. A. (2007), Input-output and Hybrid Techniques for Real-time Prediction of Delay and Maximum Queue Length at Signalized Intersections, Transportation Research Record, 2035(1), 69-80.

10.3141/2035-08

Stephanopoulos G., Michalopoulos P. G., Stephanopoulos G. (1979), Modelling and Analysis of Traffic Queue Dynamics at Signalized Intersections, Transportation Research Part A: General, 13(5), 295-307.

10.1016/0191-2607(79)90028-1

Sung N., Park J., Jo H., Lee D., Kim D., Kim Y. (2012), The Development of Highway Policies to Mitigate Traffic Congestion on Urban Area, The Korea Transport Institute, Republic of Korea.

Transportation Research Board (TRB) (2016), Highway Capacity Manual 6th Edition, National Research Council, Washington, D.C.

Wu A., Yang X. (2013), Real-time Queue Length Estimation of Signalized Intersections based on RFID Data, Procedia-Social and Behavioral Sciences, 96, 1477-1484.

10.1016/j.sbspro.2013.08.168

Journal of Korean Society of Transportation ISSN:1229-1366(Print) 2234-4217(Online) 대한교통학회지

Preview

Queue Length Estimation Algorithm for Signalized Intersections Using Taxi DTG Data

ABSTRACT

MAIN

Figure 1.

Figure 2.

Figure 3.

Figure 4.

Figure 5.

Figure 6.

Figure 7.

Figure 8.

Figure 9.

Figure 10.

Figure 11.

Figure 12.

Figure 13.

Figure 14.

References