서론
한국 경제가 장기 저성장 국면을 지나고 있는 과정에서도 내국인의 해외여행수요는 2008년 글로벌 금융위기 여파로 잠시 감소한 경우를 제외하고는 꾸준한 증가세를 유지하고 있다. 한국 사회 전반적으로 소비 심리변화와 실버 세대의 여행 증가 등 사회 전반적인 분위기가 변화하고, 단거리 노선을 중심으로 저비용항공사(Low Cost Carrier: LCC)의 국제선 노선이 확대된 결과라고 볼 수 있다. 이에 따라 그동안 침체되어 왔던 지방 항공시장이 활성화될 조짐을 보이면서 지방공항의 국제선 유치 및 신규 LCC 등장이 구체화되고 있다. 2015년 기준 내국인 국제선 이용객(outbound demand)은 연간 3천9백만 명 수준에 달하며, 이중 66.5%인 2천6백만 명 정도가 수도권 거주자로 나타나고 있다. 이러한 현실을 반영하여 그동안 내국인 국제선 항공수요의 분석과 전략은 인천공항과 김포공항을 중심으로 수도권 지역 시장분석에 치우쳐진 면이 있다. 그러나 향후 지방을 거점으로 하는 LCC의 추가 등장과 이에 따른 지방공항의 국제선 활성화를 위해서는 각 지역의 사회경제적 특성을 고려한 지역별 국제선 항공수요의 예측이 필요한 시점이다.
항공교통시스템의 독특한 기술적 측면과 경제적인 특성으로 인해 항공교통은 승용차, 철도 및 버스와 같은 타 교통수단과는 차별성을 지니는 특별한 교통수단으로 구분된다. 그러므로 지역 간 통행을 담당하는 항공수요에 대한 분석은 지역 간 통행분석에 사용되는 방법론을 일반적으로 사용하기도 하지만, 항공교통의 차별적인 특성들로 인해 그대로 적용하지 않고 추가적인 제약조건들이 덧붙여진다. 예를 들어 항공승객들은 육상교통보다 선택의 폭이 좁고, 통행의 출발과 도착지역에 따른 고유한 특성이 작용하므로 범용적인 수단선택특성을 도출하기 어렵다(Kanafani, 1983). 특히 국제선 항공수요는 경제상황, 문화현상, 국제정치 등 거시적인 요소들에 의해서도 상당한 영향을 받는 경향이 있다. 그러므로 국가전체가 아닌 특정 지역의 항공수요를 예측하기 위해서는 보다 정교한 분석기법들이 요구된다.
지금까지 항공수요와 예측에 관한 다양한 방법론이 개발되어 왔다. Rengaraju and Arasan(1992)는 선형다중회귀모형을 이용하여 도시 간 항공수요를 추정하였고, 설명변수로 인구, 가구 수, 고용율 등 뿐만 아니라 비행거리와 항공편수와 같은 공급변수들을 사용하였다. Abed et al.(2001)은 stepwise 회귀분석 기법을 이용하여 다양한 설면변수들의 조합들을 가지고 항공수요를 추정하는 다중회귀모형을 개발하였고, 최종적으로 인구수와 총소비액이 가장 설명력이 높은 사회경제변수로 선정되었다. Park et al.(2016)은 시계열 자료의 안정성을 고려한 항공수요 계량모형을 개발하였으며, 단위근 검정과 공적분 검정을 통해 시계열 자료의 특성을 검증하였다. 그리고 이에 덧붙여 시계열 자료의 안정성을 고려한 항공수요 계량경제모형 개발 프로세스를 제안하여 이를 국내선 수요 추정에 적용하였다. Lim and McAleer(2002) 또한 시계열 자료를 이용하여 국제선 항공수요를 추정하였다. 비정상성을 보이는 시계열 자료를 다루기 위해서 ARIMA 모형을 이용하였고 RMSE를 바탕으로 모형의 적합도를 검증하였다. Carson et al.(2011)은 AIM(Aggregate Individual Markets) 방법을 이용하여 거시경제변수를 적용한 항공수요예측을 수행하였다. 항공이용객의 이질성(heterogeneity)과 모형추정 불확실성간의 trade-off에 기반한 AIM 접근법은 기존의 집합적 예측모형보다 추정력에 있어서 우수함을 보였다.
전통적으로 주로 사용된 회귀분석과 시계열모형과는 다른 항공수요 예측모형도 제안되었다. Xiao et al.(2014)은 단일 spectrum 분석과 neuro-fuzzy를 결합한 모형을 사용하여 단기 항공수요 예측을 수행하였다. 단일 spectrum 분석을 통해 항공수요의 경향성과 계절성을 추출하였으며 인공지능기법을 이용하여 관측 자료의 불규칙성과 변동성을 분석하여 수요예측에 적용하였다.
본 연구에서는 최근 신공항 건설과 기존 공항의 이전과 확장이 추진되고 있는 영남권(부산, 대구, 울산, 경북, 경남)을 대상으로 지역 국제선 항공수요 예측 모형을 제안하고자 한다. 우선적으로 국제선 항공수요에 영향을 주는 핵심요인들을 선별하고 이를 설명변수로 하는 다양한 계량졍제모형을 테스트하고 이중에서 영남권 국제선 항공수요를 가장 잘 설명할 수 있는 모형을 도출한다. 일반적으로 계량경제모형에서는 사용하는 설명변수들의 종류는 매우 제한적이다. 이것은 종속변수를 설명하는 모든 변수들을 찾아내서 사용하는 것은 현실적으로 불가능하기 때문이며, 이러한 이유로 누락변수편의(omitted variable bias)와 미관찰 이질성(unobserved heterogeneity)는 항상 주의를 기울여야 하는 문제이다. 따라서 본 연구에서는 제한된 설명변수를 사용할 수밖에 없는 항공수요 추정모형에서 관측되지 않은 영남권의 특성을 반영할 수 있는 방법을 찾고자 하였다.
방법론
1. 국제선 항공수요 결정 요인
항공수요를 결정짓는 사회경제적 변수들은 다양하게 존재하며, 항공사가 제어할 수 있는 요소들과 제어 밖에 있는 것들로 구분할 수 있다. Jorge-Calderon(1997)은 첫 번째 요소를 지리경제적 요인으로, 두 번째 요소들을 서비스관련 요인으로 각각 칭하였다. 지리경제적 요인들은 활동변수와 지역변수로 추가 구분할 수 있으며, 이중 활동변수들은 항공서비스가 제공되는 대상자들의 경제적, 문화적 및 정치적 특성에 영향을 받는다. 관련 연구에서 가장 보편적으로 사용된 설명변수로는 인구수와 국내총생산(GNP) 또는 지역내총생산(GRDP)으로 표현되는 경제성장규모이다. 이와 함께 추가적으로 소득과 항공요금 등이 사용되고 있으며, 이러한 변수들은 여러 형태로 정의되고 다양한 분석목적에 적용하고 있다. 예를 들어 소득은 총소득 또는 가처분 소득으로 구분해서 적용할 수 있으며, 일반적으로 GNP와 소득은 각각 업무 통행과 비업무 통행 수요 추정에 사용하게 된다(Karlaftis et al., 1996). Valdes(2015)는 중위소득국가에서는 소득 증가율과 소득탄력도가 총 여객수요의 75% 정도를 설명한다고 주장하였고, ‘Open Skies Agreements’와 같은 공공 정책이 여객증가에 긍정적인 작용을 하며 LCC 성장은 상대적으로 부차적인 영향을 주는 것으로 분석하였다.
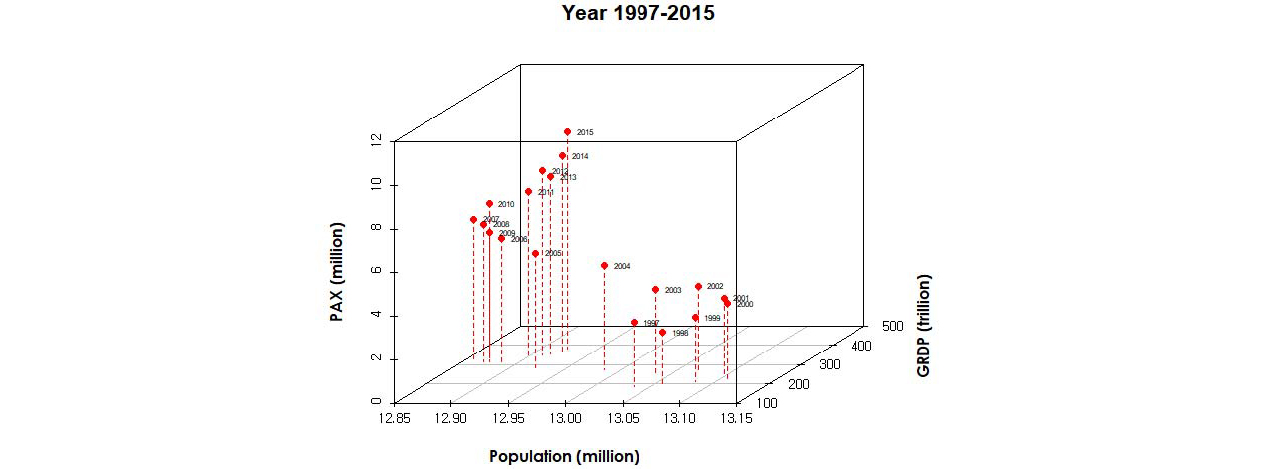
관련 연구에서 밝혀진 바와 같이 과거 영남권 국제선 이용객 수요를 가장 잘 설명하는 모형을 구축하기 위해서 설명변수로는 인구수와 GRDP를 선정하였으며, 이는 설명변수의 선정에 있어서 변수의 설명력과 함께 해당 자료의 습득가능성과 자료의 신뢰성도 함께 고려한 결과이다. 과거 영남권 인구와 지역내총생산 자료로는 통계청과 한국은행에서 제공하는 공식 수치를 사용하였다. 설명변수인 영남권 인구와 GRDP는 공인된 수치가 존재하는 반면에 종속변수인 영남권 국제선 이용객수는 공식적으로 발표되는 자료는 없어 관련 공식자료로부터 추정해내는 과정이 별도로 필요하다. 내국인이 국제선을 이용할 때는 반드시 출입국 심사를 통과해야 하므로 내국인의 국제선 총 이용수요는 매년 정확하게 집계되고 있다. 그러나 2006년에 내국인의 출국신고서 작성이 완전 폐지된 이후에는 출국하는 내국인의 주소지 통계를 알 수 없어 지역별 국제선 이용객에 대한 통계는 직접적으로 발간되지 않고 있다. 따라서 본 연구에서는 매년 법무부에서 발간하는｢출입국 통계연보｣(법무부, 각 년도)에 제시되어 있는 공항별 내 ‧ 외국인출입국자 비율을 적용하여 산출하였다. 다만 출입국 통계연보의 내 ‧ 외국인 합과 국제선 이용객 수의 합이 다소 차이가 있어 전체 국제선 이용객 수의 경우에는 보다 정확하다고 판단되는 한국공항공사의 통계수치를 사용하고, 법무부 통계연보에서는 내 ‧ 외국인 비율만을 적용하였다. 영남권 국제선 이용객 수요 추정을 위해 수집된 관측 자료를 3차원 그래프를 이용하여 살펴보면 다음과 같다.
2. 다중회귀 모형
계령경제모형들은 전형적으로 다수의 경제 변수들 간의 관계를 분석하는 것을 목적으로 하고 있으며, 회귀분석은 이러한 관계를 분석하는데 있어서 다양한 도구를 제공한다(Ashenfelter et al., 2003). 따라서 영남권 항공수요예측을 위한 방법으로 가장 먼저 다중회귀모형을 선택하여 추정하였다. 앞서 도출된 인구수와 GRDP를 설명변수로 하고 국제선 이용객 수를 종속변수로 한 다중회귀모형식과 모형 추정결과는 다음과 같다.
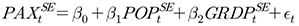(1)
여기서 추정된 다중회귀모형이 영남권 과거 국제선 여객수요 관측치를 얼마나 편향되지 않으면서 안정적으로 설명하고 있는 가를 평가하는 지표로 평균제곱오차(mean squared errors, MSE)를 사용하였으며 계산식은 다음과 같다.
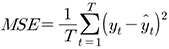(2)
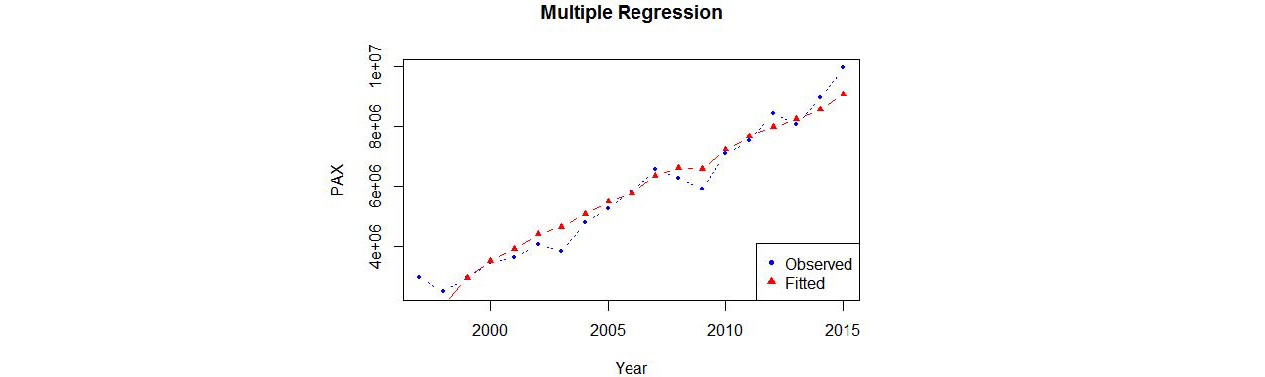
앞서 구축한 영남권 국제선 이용객 과거 실적(1997-2015년)에 대한 다중회귀모형의 MSE 값은 ‘11,452, 519,145’ 이며,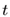 
시점에서 관측값과 추정값의 비교는 Figure 2에서 제시된 바와 같다. 영남권 과거 실적자료만을 사용한 다중회귀분석 모형의 추정결과를 보면 설명변수 중에서 GRDP만 통계적으로 유의하게 나타나고 인구수는 설명력이 없는 것으로 판단된다. 그럼에도 불구하고 영남권 자료에 대한 회귀분석모형은 
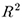값(=0.9487)이 매우 높고, 관측값와 추정값의 비교 그래프를 보더라도 다중회귀 모형식이 영남권 국제선 이용객 증가 추이를 잘 묘사하는 것처럼 보인다.
따라서 OLS(Ordinary Least Squares)로 추정한 다중회귀모형의 적합성 여부를 판단하기 위해서 보다 세밀한 통계분석이 필요하다. OLS는 회귀모형의 오차항은 동일한 분산(등분산성: homoscedasticity)을 가지며, 서로 독립적(independence: no autocorrelation)이라고 가정하여 모형을 추정하는 방식이다. 회귀모형에서 오차항은 측정할 수 없으므로 오차항에 대한 추정치가 필요한데 이를 잔차(residual)라고 한다. 오차의 가정은 잔차에 의해 성립여부를 판단할 수 있으므로 오차항에 대한 가설검증은 추정된 회귀식의 잔차를 이용하여 다음과 같은 테스트들을 통해 수행하게 된다.
- 등분산성 가설 검증을 위한 Breush-Pagan test 결과: BP = 0.4004, df = 2, p-value = 0.8186
- 독립성 가설 검증을 위한 Durbin-Watson test 결과: DW = 0.76224, p-value = 0.00023
다중회귀모형 오차항에 대한 두 가지 가설검증 결과를 살펴보면, 오차항의 분산은 동일하나 자기상관(autocorrelation, serial correlation)이 존재함을 알 수 있다. 회귀분석에 사용된 변수들이 모두 시계열 자료인 경우에 회귀분석모형의 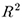값이 매우 높으면서 잔차에 autocorrelation이 존재하면 허구적 회귀(spurious regression) 가능성을 검증할 필요가 있다. 앞서 사용한 변수들이 불안정적인(non-stationary) 시계열 자료이면 실제 변수들 간에는 아무런 상관이 없음에도 불구하고 외견상 연관관계가 있는 것처럼 판단하는 오류가 발생할 가능성이 있으며, 이를 허구적 회귀라고 한다. 불안정적인 시계열을 포함한 회귀분석이 항상 허구적이지는 않으며, 만약 독립변수가 충분히 외생적이라면 불안정적인 시계열이 설명변수로 사용된다 하더라도 허구적 회귀현상이 나타나지 않게 되고 이런 경우에는 변수들 간에 공적분(cointegration)이 존재한다고 한다(Ashenfelter et al., 2003; Stock and Watson, 2007). 다중회귀모형에 대해서 공적분을 검증하기 위해 회귀모형에 사용된 변수들과 추정된 잔차의 정상성(stationarity)에 대한 Augmented Dickey-Fuller test를 수행한 결과는 다음과 같다.
위 ADF test 결과를 살펴보면 다중회귀모형에 사용된 모든 변수들이 비정상적(non-stationary) 시계열임을 알 수 있다. 그런데 추정한 회귀모형의 표준화된 잔차에 대해서도 마찬가지로 비정상성이 발견되어 이 경우에는 공적분이 있다고 볼 수 없다. 그러므로 앞서 제시된 바와 같이 다중회귀분석모형의 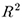값이 매우 크고 영남권 국제선 이용객 증가 추이를 잘 묘사하는 것처럼 보이지만, 여기서 도출된 상관관계는 허구적이라고 판단된다.
영남권 자료만을 가지고 다중회귀분석을 시행한 결과 허구적 회귀관계가 발견되어서 현재 모형은 장래 영남권 국제선 이용객 수요를 추정하기에 적합하지 않다고 판단된다. 이와 같은 허구적 회귀는 변수 값의 차분(difference)를 이용하여 해결하는 방안도 존재하지만, 국제선 이용객에 영향을 주는 것으로 이미 잘 알려져 있는 인구수가 현재 다중회귀모형에서는 통계적으로 유의하지 않다는 점도 영남권 자료만을 사용해서 추정한 다중회귀모형이 아닌 다른 계량경제모형 대안을 찾아야 되는 주된 이유이다.
3. 패널 자료(panel data) 분석
앞서 다룬 회귀분석모형이 통계적으로 유의하지 않을 뿐만 아니라 허구적 회귀를 보여준 것만을 바탕으로 우리가 사용한 인구수와 GRDP가 국제선 항공수요를 설명하지 못한다고 단정 짓는 것은 매우 성급한 판단이다. 아마도 영남권 국제선 수요를 설명하는 중요한 변수들을 우리가 모형에 포함시키지 못함에 기인했을 수 있다. 그러나 더 큰 문제는 이러한 누락변수가 관측이 불가능한 경우이다. 즉 국제선 항공수요를 설명할 수 있는 어떤 중요한 사회경제적 변수가 우리가 현실적으로 이용 가능한 database에 포함되어 있지 않다거나, 본질적으로 관측이 불가능하다는 의미이며 이러한 문제를 ‘미관찰 이질성’이라고 부른다(Ashenfelter et al., 2003). 다행히도 횡단면 자료와 시계열자료를 결합한 패널 자료를 사용하면 이러한 혹시 존재할 수 있는 ‘미관찰 이질성’ 문제를 효과적으로 다룰 수 있는 방법이 존재한다.
패널 자료를 이용한 사회경제현상 분석은 이미 다양한 분야에서 효과적으로 사용되고 있으며, 특히 관측이 쉽지 않은 요인들이 중요한 설명변수일 것으로 예상될 때 많이 활용된다. 예를 들어, 보트난민이 지역 노동시장에 미친 효과(Card, 1990), 보수 성향 뉴스가 지역 유권자의 투표에 미친 효과(DellaVigna and Kaplan, 2007), 노조 가입이 임금에 미치는 효과(Freeman, 1984) 등 단순히 몇 개의 관측 가능한 설명변수들 만으로는 종속변수를 통계적으로 유의하게 설명하기 어려운 사례들에 대해서 패널 자료를 이용한 분석은 매우 성공적으로 판명되어오고 있다. 이처럼 패널 자료 분석은 다음과 같은 중요한 장점을 가지고 있어, 앞서 한계점들이 노출된 영남권 자료만을 이용한 다중회귀모형 보다 영남권 국제선 수요예측에 사용하기 적합할 것으로 예상된다.
i) 단순 횡단면(cross-section) 분석과 시계열(time series) 분석의 한계를 극복
ii) 국제선 이용객에 영향을 미치지만 관측이 되지 않는(또는 관측 자료에서 누락된) 설명변수들에 의한 편이(bias) 통제할 수 있음: 미관찰 이질성
iii) 광역권별로 고유한 내재적 속성(고정효과: fixed effects)의 존재를 고려할 수 있음
패널 자료 분석을 위해 전국을 광역권으로 구분하여 권역별 인구와 GRDP 및 해당 권역의 국제선 이용객에 대한 1997년부터 2015년까지의 과거 실적치를 수집하였으며, 광역권들의 구분은 다음과 같이 하였다.
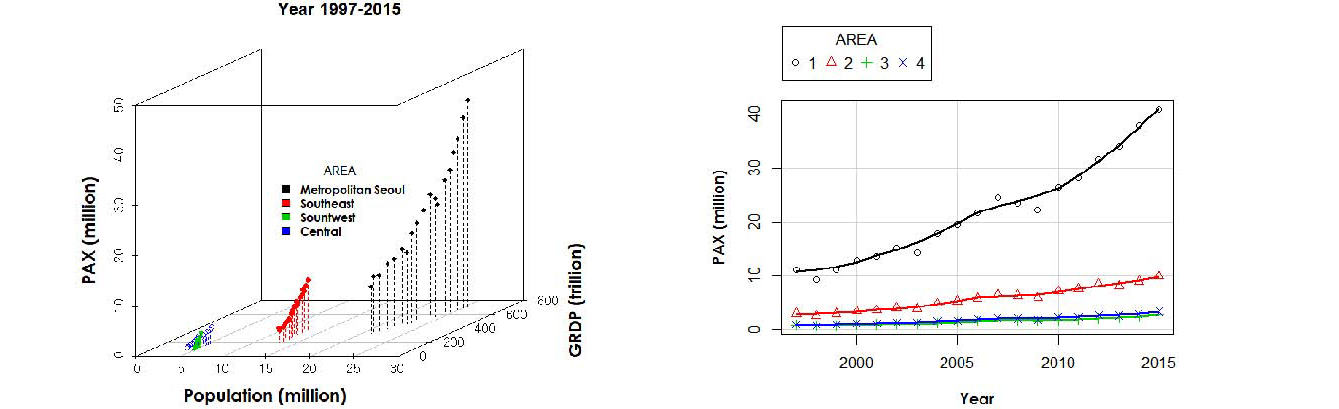
장래 영남권 국제선 이용객 예측을 위한 계량경제모형 개발에 사용할 자료는 지역별 특성을 구분할 수 없는 우리나라 전체 합인 ‘전국’ 관측치를 먼저 제외하고, 다른 광역권들과 국제선 이용객 규모와 통행 특성이 상이한 ‘관동권’과 ‘제주’ 또한 배제하였다. 따라서 모형 구축에 사용된 최종 관측 자료의 총 개수는 4×19=76 (4개 광역권×19년)이며, 이는 패널 자료 형태로 구축되었다. 패널 자료 분석에 사용된 관측 자료는 Figure 3에서 볼 수 있는 것처럼 다양한 수준에서 분포하고 있다.
1) Pooled OLS 회귀모형(regular OLS regression model: pooling model)
먼저 패널 자료의 횡단면과 시계열 특성을 구분하지 않고 동일한 관측값으로 처리하는 ‘Pooled OLS 회귀모형’을 테스트해보는 것은 상당한 의미가 있다. 이러한 정규 OLS 회귀모형은 광역권간 또는 관측년도간의 이질성(heterogeneity)를 전혀 고려하지 않는다. 따라서 앞서 테스트한 다중회귀모형이 영남권에 대한 19개의 관측값만을 사용한 것에 비해서, 본 모형은 각기 다른 특성의 4개 광역권들에 대한 총 76개 관측치를 활용함으로써 모형추정에 사용되는 자료수를 늘이고 설명변수 값의 변동성이 커진 것에 대한 효과를 검증해 볼 수 있다. Pooled OLS 회귀모형식과 모형 추정결과는 다음과 같다.
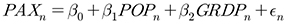(3)
모형추정 결과를 보면 앞서 개발한 영남권 자료만을 이용한 다중회귀분석 모형에 비해 국제선 이용객 수요를 인구수와 GRDP를 통해 매우 잘 설명하고 판단할 수 있다. 특히 영남권 자료 모형에서는 통계적으로 유의하게 설명되지 않았던 인구수 요인이 본 모형에서는 분명하게 도출되었다. 그리고 모형 전체의 설명력을 나타내는 값 또한 매우 높게 추정되었다. 이는 다양한 수준의 관측값을 가지는 4개 광역권의 자료들을 모두 다중회귀 모형 추정에 사용하였기 때문으로 파악된다.
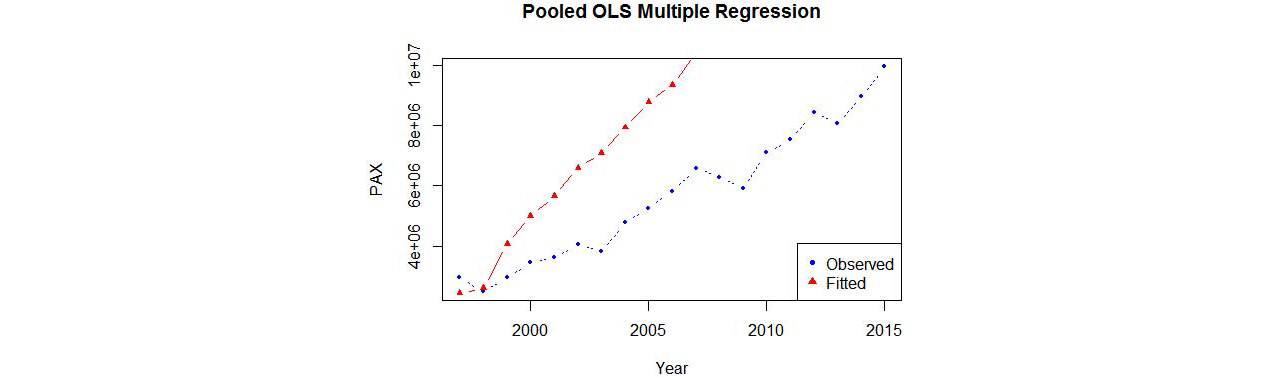
그러나 이러한 추정결과만을 근거로 4개 광역권 자료를 모두 이용한 다중회귀분석 모형이 영남권 국제선 이용객 수요를 정확하게 예측할 것이라고 판단하는 것은 성급하다. 왜냐하면 4개 광역권 모두 인구수와 GRDP 만으로는 설명할 수 없는 개별적인 지역 특성이 분명히 존재하기 때문이다. 즉, 광역권별로 미관찰 이질성이 해당 광역권의 국제선 이용객 수요에 상당한 영향을 준다는 것이 분명하기 때문이다. 이에 따라 패널 자료를 이용해 추정한 다중회귀모형식의 영남권 국제선 이용객 과거 실적에 대한 설명력을 우선적으로 검증할 필요가 있다. 이를 위해 영남권 자료에 대해 추정 모형의 MSE 값을 구한 결과는 ‘745,171,626,780’으로 산출되었으며, 이는 앞서 개발한 영남권 자료만을 이용한 다중회귀모형의 MSE 값(11,452,519,145)에 비해 약 64.1배(6,401%)에 증가하여 모형의 설명력이 현저히 낮아졌다고 판단된다. 이러한 낮은 모형 설명력은 Figure 4에서 제시된 과거연도별 관측값과 추정값의 차이를 통해서도 직관적으로 확인할 수 있다. 이는 추정모형이 4개 광역권 전체에 대해서는 평균적으로 잘 설명하고 있지만 영남권 고유의 특성을 반영하지 못함으로 인해 영남권 장래 국제선 이용객 추정에 사용하기에는 적합하지 않다는 것을 의미한다.
2) Fixed-effects model
앞서 살펴본 바대로 4개 광역권의 패널 자료를 일반적인 OLS 다중회귀모형을 이용해서는 광역권간에 고유의 특성과 시계열적 변동 요인들을 고려할 수 없다. 그러므로 본 연구에서는 영남권 국제선 수요예측에 panel data regression 모형 중에서 광역권 고유의 특성을 추정할 수 있는 fixed-effects model을 사용하였고 모형의 형태는 다음과 같다.
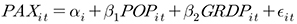(4)
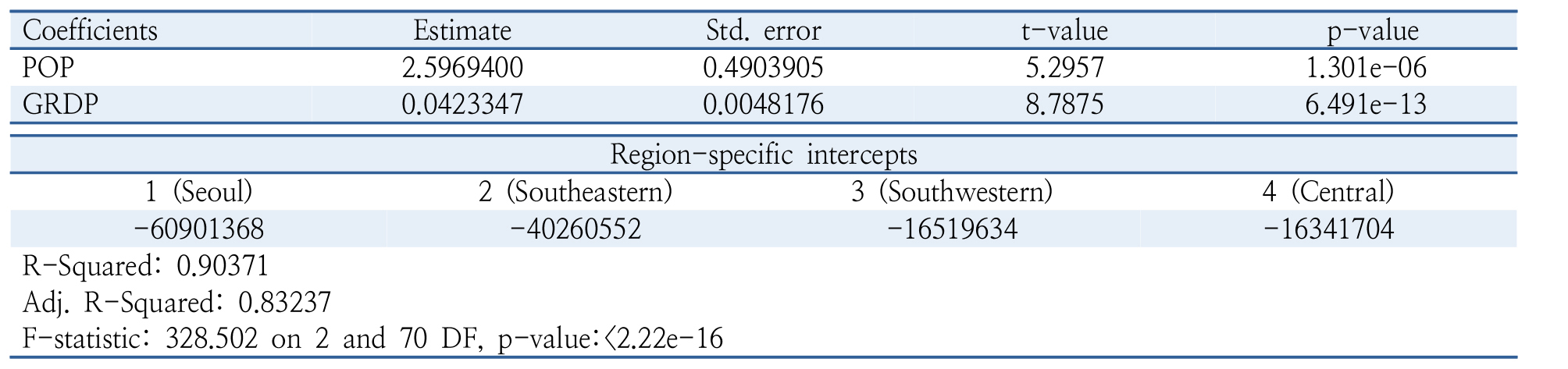
Fixed-effects model의 추정결과는 Table 5에 제시된 바와 같으며, 설명변수로 선택한 광역권 인구와 GRDP 모두 통계적으로 유의하다고 판정되었고 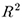값과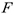 
-statistic을 바탕으로 panel regression model의 통계적 유의성을 검증할 수 있다.
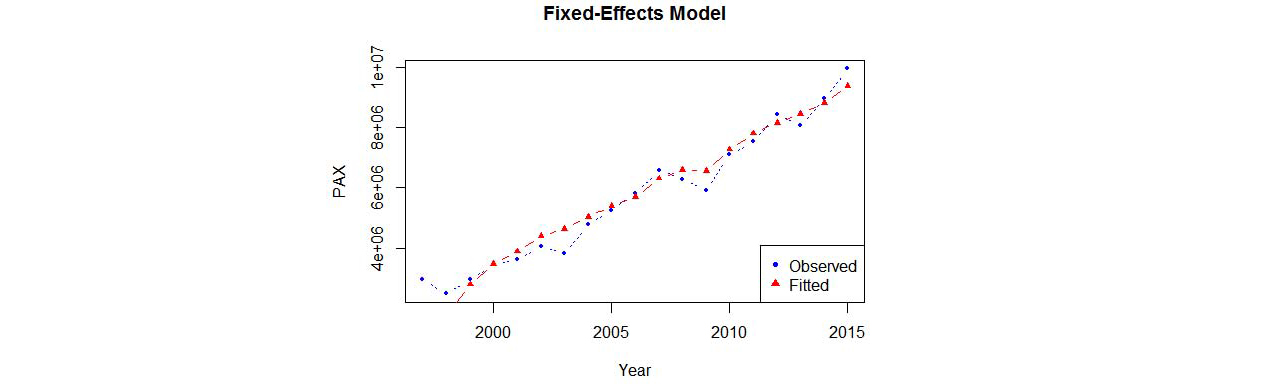
국제선 항공기 이용객 수요를 결정한다고 알려져 있는 인구수가 fixed-effects model에서 확실한 설명력을 보여주는 것은 인구수, GRDP 및 국제선 이용객 수요에 대한 횡단면과 시계열 측면에서 다양한 수준을 보이는 관측 값들을 이용하여 모형계수를 추정하였기 때문으로 파악된다. 추정계수의 높은 통계적 유의성 검증과 더불어 영남권 과거 국제선 이용객 실적(1997년-2015년)에 대한 fixed-effects 모형의 관측값과 추정값을 비교해보면 Figure 5에서와 같이 추정 모형이 현상을 매우 잘 묘사하는 것으로 나타난다. 특히 fixed-effect 모형이 변수 값의 범위가 매우 다양한 전국 4개 광역권 패널 자료를 모두 이용해서 추정하였음에도 불구하고, 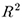값이 상당히 높고 영남권 관측치에 대한 MSE 값이 ‘12,718,493,932’로 변수 값의 범위가 상대적으로 작은 영남권 자료만을 사용한 다중회귀분석모형의 MSE 값(11,452,519,145)과도 대비해서 11.05% 정도만 증가한 것으로 나타났다. 또한 충분히 예상할 수 있는 바대로 fixed-effect model이 앞서 폐기한 pooled OLS 회귀모형에 비해 광역권별과 시계열적 영향(individual and/or time effects)을 보다 잘 설명하는 지 여부를 테스트한 결과도 다음과 같이 산출되어 fixed-effects model을 선택하는 것이 바람직하다고 판단된다.
F test for individual effects
- Null hypothesis: OLS better than fixed
- Alternative hypothesis: significant effects
- Test statistics: F = 53.597, df1 = 3, df2 = 70, p-value<2.2e-16
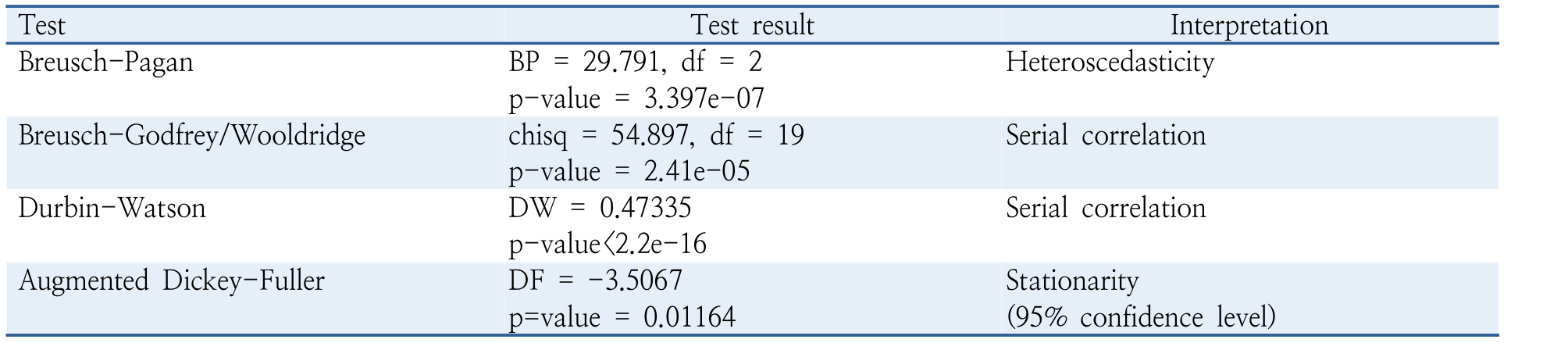
그러나 fixed-effects model을 영남권 장래 국제선 이용객 추정모형으로 판단하기 위해서는 OLS 다중회귀모형에 마찬가지로 추정모형 잔차에 대한 세부적인 가설 검증과 함께 패널 공적분(panel cointegration) 검증을 시행하는 것이 필요하다. Fixed-effect model의 잔차에 대한 가설 검증 분석 결과는 다음과 같다.
Fixed-effects model은 비정상성 시계열 자료를 변수로 사용하였으나 95% 신뢰수준에서 잔차가 정상성(stationarity)을 보여 cointegration이 존재함을 알 수 있다. 그러므로 잔차에 자기상관이 존재함에도 불구하고 앞서 제시된 fixed-effects model의 상당히 높은 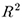값과 상대적으로 우수한 MSE는 전혀 허구적이지 않고 모형의 설명력을 실질적으로 의미한다고 판단된다.
3) Random-effects model
패널자료 분석에 사용되는 random-effects model은 fixed-effects model와는 다르게 광역권간의 변이는 random 하며 모형 설명변수들과는 상관관계가 없다고(uncorrelated) 가정하는 모형이다. 4개 광역권 패널 자료를 이용하여 추정한 random-effects model의 모형식과 모형 추정결과는 다음과 같다.
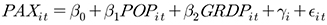(5)
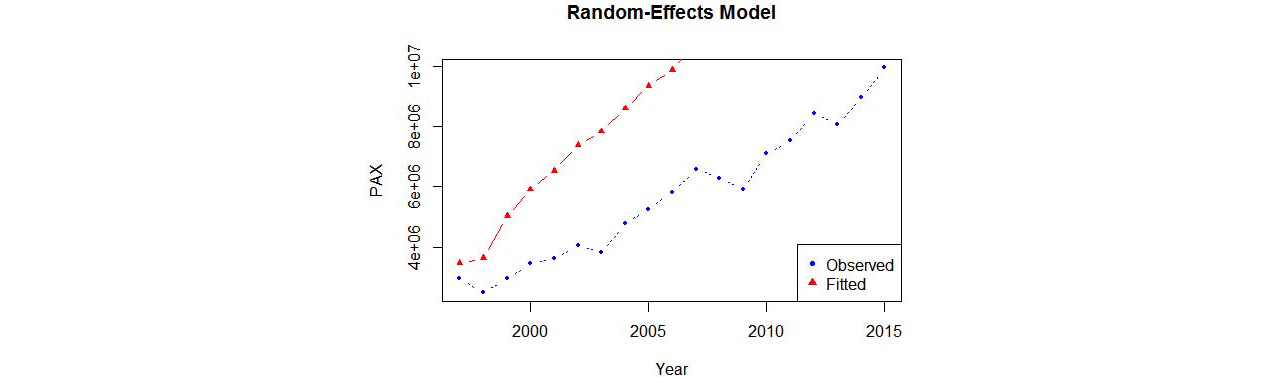
Fixed-effects model에서와는 다르게 random-effects model에서는 인구수가 국제선 이용객 수요에 대한 통계적으로 유의한 설명을 하지 못한다고 도출되었다. 이는 영남권 자료만으로 추정한 다중회귀모형에서와 동일한 추정결과로서, random-effects model이 영남권 장래 국제선 수요를 추정하는 데 적합하지 않다는 것을 의미한다. Random-effects model은 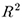값이 다른 모형에 비해 상당히 낮아졌고, 영남권 관측치에 대한 MSE 값 또한 ‘924,534,056,486’로 산출되어 영남권 자료만을 사용한 다중회귀분석모형의 MSE 값(11,452,519,145)과도 대비해서 79.7배(7,970%) 정도 증가함으로써 모형의 설명력이 매우 낮다고 판단된다. Figure 6에서 직접적으로 파악할 수 있는 것처럼 영남권 과거 관측시점별 통계값과 모형 추정값의 차이를 통해서도 random-effects model의 비적합성을 재차 확인할 수 있다.
4. 영남권 국제선 수요추정을 위한 모형 선정
지금까지 영남권 국제선 수요 추정에 적합한 모형을 찾기 위해 4가지의 다양한 계량경제 모형들을 구축하여 세밀한 통계적 분석을 시행하였다. 먼저 영남권 관측 자료만을 활용한 다중회귀모형은 항공수요의 핵심적인 설명변수인 ‘인구수’가 통계적 유의성을 확보하지 못했다. 한편 관측치와 모형 추정치간의 goodness-of-fit는 매우 우수하게 나타났으나, 전형적인 불안전적 시계열 자료의 ‘허구적 회귀’ 현상을 보여주었다. 따라서 본 연구에서는 4개 광역권에 대한 패널 자료를 구축하여 패널 자료 분석방법을 사용하는 것이 바람직한 것으로 판정되었다.
첫 번째로 테스트한 ‘Pooled OLS 회귀모형’에서는 설명변수인 인구수와 GRDP 모두가 국제선 이용객 수요를 매우 잘 설명하고 있으며 모형 전체의 설명력을 나타내는 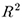값 또한 매우 높게 추정되었다. 매우 흥미로운 현상은 앞서 테스트한 영남권자료만을 사용한 다중회귀모형과는 반대로 ‘인구수’ 변수도 통계적으로 유의한 것으로 나타났으나, 모형의 goodness-of fit 지표는 상대적으로 매우 낮아졌다. 이는 다양한 수준의 관측값을 가지는 4개 광역권의 자료들을 모두 사용함으로써 모형의 전체자료에 대한 설명력은 높아졌으나 특정 지역인 영남권에 대해서는 지역 고유 특성을 반영하지 못한 결과로 모형 적합도가 낮아진 것으로 파악된다.
패널 자료 분석에 자주 사용되는 random-effects model에서는 매우 독특한 현상이 관측되었다. ‘영남권자료를 이용한 다중회귀모형’과 ‘Pooled OLS 회귀모형’에서 도출된 두개 단점들이 동시에 나타났다. 영남권 모형에서와 동일하게 ‘인구수’ 설명변수가 통계적으로 유의하지 않음과 동시에 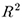값이 상당히 낮아지고 goodness-of-fit 지표도 매우 악화되어 모형의 설명력이 매우 낮다고 판단된다. 추가적으로 random-effects model의 적합도를 pooled OLS 모형과 fixed-effects model에 대한 상대비교를 통해 재차 검증하였으며, 가설검증 결과는 다음과 같다.
먼저 random effects에 대한 Breusch-Pagan Lagrange Multiplier 값을 살펴보면 광역권들 간에 통계적으로 유의미한 차이(significant differences)가 존재한다고 분석되었으며, 따라서 단순한 pooled OLS 회귀모형보다는 random-effects model을 사용하는 것이 적합하다고 판단된다. 그러나 random-effects model이 fixed-effects model 보다 선호된다는 귀무가설을 가지는 Hausman test를 실행한 결과를 보면 매우 낮은 p-value가 산출되어 귀무가설이 쉽게 기각되면서 fixed-effects model을 사용하는 것이 통계적으로 타당한 것으로 도출되었다. 이는 광역권별 고유의 errors(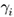
)와 설명변수들(regressors) 간에 상관관계가 존재한다는 것을 의미한다.
Random-effects model 분석을 통해 흥미로운 현상을 통해 국제선 항공수요 모형 구축의 핵심 사항은 ‘미관찰 이질성’을 어떻게 잘 처리하여 광역권별 고유의 특성을 최대한 반영할 수 있는가에 있다는 것을 확인할 수 있다. 결론적으로 직접 관찰하거나 측정하기 어려운 광역권별 고유 특성을 패널 자료를 이용하여 추출해낸 fixed-effect model이 영남권 국제선 수요 추정에 가장 적합한 모형으로 판단된다.
다양한 모형대안들 중에서 최적 모형을 선정하는데 있어서 모형구조와 변수들에 대한 통계적 검증이 매우 중요하다. 그러나 이와 함께 모형의 실제 적용성에 대한 판단도 고려되어야 한다. 이론적으로 정교하고 모형 추정치에 대한 통계적 합리성이 확보되었다 하더라도 직관적으로 추정 모형의 구조와 계수가 직관적으로 이해하기 어렵다면 실제 예측에 사용하기 쉽지 않다. 최종적으로 선정한 fixed-effects 모형은 광역권별 고유 특성을 집합적으로 표현하는 고유 절편값들을 제공함으로써 추정 모형의 합리성을 직관적으로 평가할 수 있어 모형의 실제 적용시 모형의 설명력을 증가시켜준다. 또한 시계열적으로 다른 자료들을 사용하여 추정된 고유 절편값들의 변화를 비교함으로써 광역권별 고유특성을 모형이 얼마나 잘 반영하고 있는지를 추가적으로 검증해 볼 수 있다.
결론
본 연구의 목적은 미관찰 지역 특성을 고려한 영남권 국제선 항공수요 추정 모형의 개발이다. 기존 연구에서 주로 사용하였던 시계열 자료를 이용한 회귀분석모형과 시계열 모형에서 다루기 어려웠던 지역 고유 특성을 합리적으로 모형에 반영하는 것에 중점을 두었다. 이를 위해 패널 자료 분석기법을 사용하였으며, 이를 기존 다중회귀모형과의 비교분석을 통하여 본 연구에서 개발한 fixed-effects model의 합리성과 적정성을 증명하였다. 영남권 항공수요 추정을 위한 대안 모형들은 먼저 모형추정결과에 대한 통계적 유의성 검증을 거쳤고 모형 전체의 적합성을 판단하기 위해 MSE를 기반으로 하는 goodness-of-fit 수치를 검토하였다. 영남권 자료만을 사용한 모형과 4개 광역권 자료를 패널 자료화하여 모두 사용하는 모형을 검증하는 과정에서 시계열 자료를 사용한 회귀분석에서 자주 나타나는 ‘허구적 회귀’ 현상을 발견할 수 있었고, ‘미관찰 이질성’에 때문에 발생한 통계적 비유의성과 낮은 모형 적합도를 관측하게 되었다.
본 연구를 통해 그동안 다른 사회경제관련 분야에서 활발히 사용되어온 패널 자료 분석기법을 항공수요 추정에도 효과적으로 적용할 수 있음을 보여주었다. 횡단면자료와 시계열자료를 결합된 형태인 패널 자료는 자료 취득의 어려움과 통계적 검증의 복잡성으로 일반 시계열보다 시간과 비용이 더 많이 소요되는 단점이 존재하고, 일반적인 회귀분석모형에 대한 상대적 적합성 또한 분석 대상과 활용 자료의 성격에 따라 달라질 수 있다. 이러한 한계에도 불구하고, 본 연구는 국제선 항공 수요 예측과 같이 소수의 핵심적인 거시 사회경제지표에 의존할 수밖에 없는 분야에서 패널 자료 분석의 유용성을 확인하는 의미 있는 사례로 평가받을 수 있다고 판단된다.
우리나라 장래 교통수요 예측에 기본적으로 사용되는 KTDB(Korea Transport Database)를 살펴보면 국내 인구가 감소하는 2025년을 기점으로 모든 교통수단별 통행량이 줄어드는 패턴을 보이고 있다. 그러나 국내외에서 지금까지 관찰된 현상을 살펴보면 지속적인 경제성장과 관광 ‧ 여가에 대한 관심의 증가로 인해 항공과 고속철도와 같은 고급 교통수단에 대한 1인당 연간 이용횟수는 꾸준히 증가해오고 있다. 따라서 인구수에 기반을 둔 KTDB 만으로 충분히 합리적으로 예측하기 어려운 항공수요 분야에 있어서 다양한 이론과 방법론에 대한 연구 및 실제 사례적용이 활발하게 이루어져야 할 시점이라고 여겨진다. 본 연구에서 개발된 패널 분석 모형은 국내 항공수요 분석에 이미 일부 적용된 사례도 있어, 여기서 제시된 연구결과가 다양한 항공수요 추정 방법 개발 노력의 일환으로 평가받을 수 있을 것으로 기대한다.
국내선 항공, 고속철도, 고속페리 등 이용수요특성에 있어서 일반 육상교통과는 상당한 차이가 있는 분야의 이용행태 분석 및 수요예측에 패널 회귀 모형이 본격적으로 적용되기 위해서는, 본 연구에서 다룬 공간적 범위보다 더욱 세분화된 도시별, 항공시장별 항공수요예측 모형의 개발이 필요하다. 특히 본 연구에서 포함시키지 못한 취항도시, 운행편수, 공항 접근성 등과 같은 공급관련 미시적인 설명변수 뿐만 아니라 경제위기와 전염병 발병과 같은 일시적 항공시장 충격요인들을 반영한 항공수요 예측 모형 개발이 향후 핵심 연구방향으로 여겨진다.
