서론
선행연구
용어설명
1. 항공기 연료의 정의
2. 기상예보(TAF)의 정의
3. Safety Analysis and Assessment의 정의
연구방법론
1. 기상예보와 재량연료량과의 다중회귀분석
2. 경제적인 재량연료 탑재량 분석
결론
서론
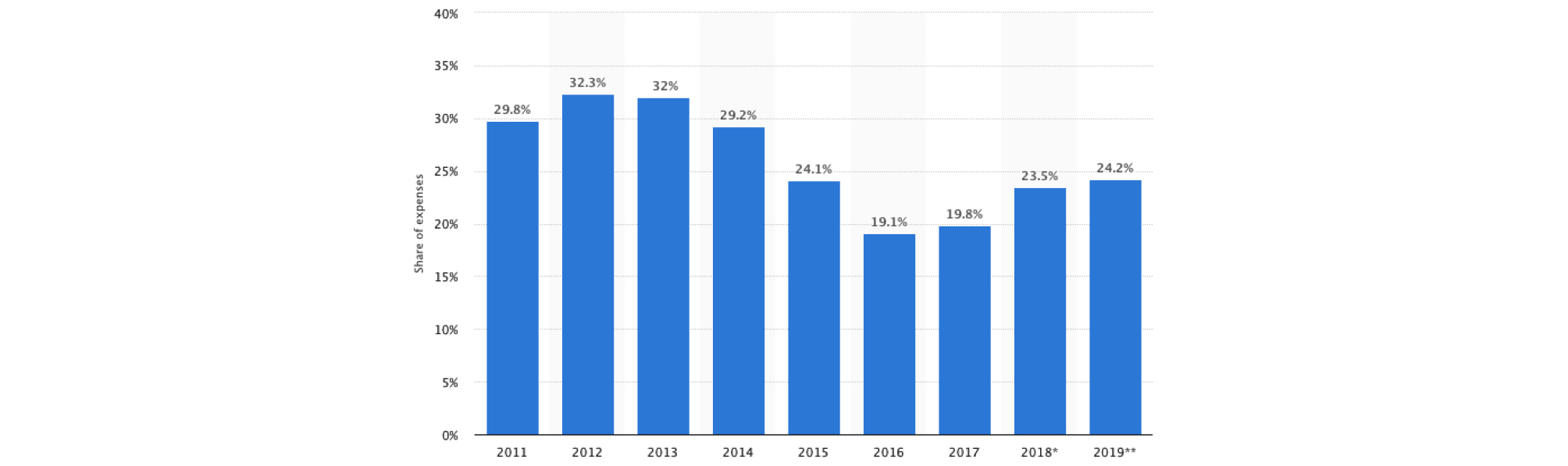
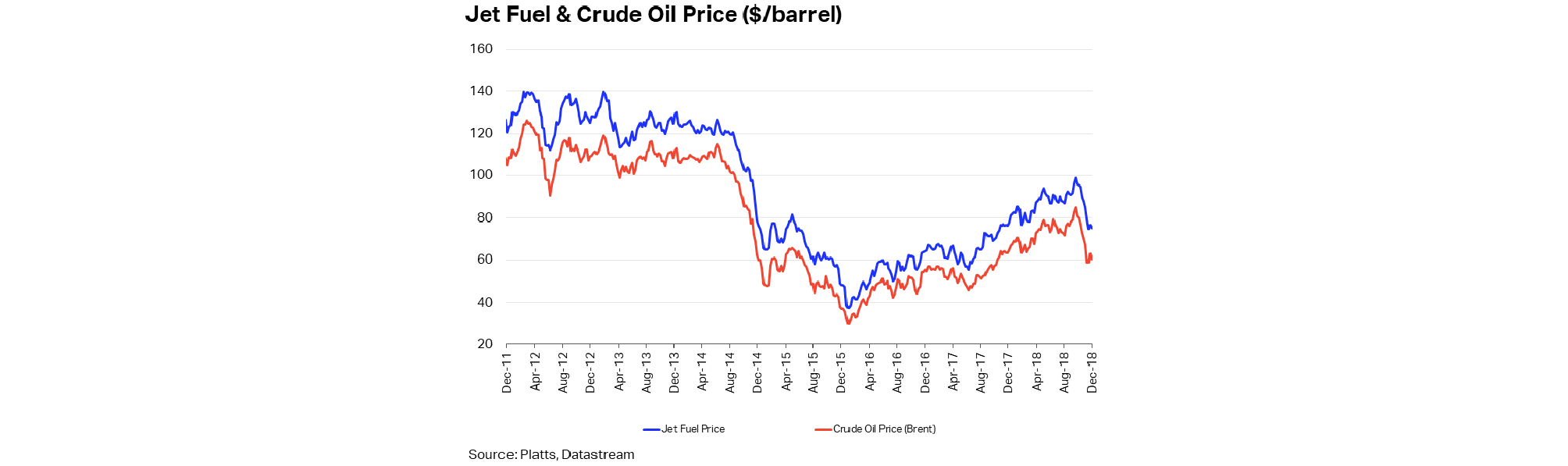
세계 항공운송산업은 자유화와 개방화가 시작된 이후로 전 세계 항공사간의 경쟁이 가속화 되고 있고 국내에서는 2000년 중반 저비용항공사의 등장으로 우리나라의 항공산업 또한 비약적인 발전과 동시에 경쟁이 치열해지고 있다. 항공사들은 경쟁 속에서 살아남기 위해 운영비용을 절감을 위한 다양한 노력을 하고 있다. 연료비용은 항공사 전체 운영비용 중 평균 약 25% 이상을 차지하고 있고 국제유가 변동에 따라 19부터 32%까지 영향을 미치고 있다(Figure 1, 2 참조).
따라서 항공사들은 이 연료비용을 최소화하기 위하여 최신 기종 도입, 최소한의 기내물품 탑재, 고효율 엔진으로 교체, 지상에서의 연료 소모 최소화, 동체 페인트를 벗겨내는 등 다양한 노력을 하고 있다. 이 중에서도 연료비용을 절감할 수 있는 가장 효과적인 방법은 운항을 위한 계획연료와 실제 사용연료의 오차를 최소화 하는 것이다. 운항을 위한 연료는 반드시 탑재해야 하는 법정연료(legal fuel)와 항공사의 정책(Company Compensation Fuel, CCF), 조종사와 운항관리사에 의해 탑재하는 재량연료(discretionary fuel), 출발지의 연료가격이 목적지 보다 저렴할 때 연료를 더 탑재하는 Tankering fuel 등의 추가연료(extra fuel)가 있다. 추가연료 중에서 재량연료에 대한 탑재기준을 참고할 수 있는 법, 매뉴얼, 가이드라인이 없어 개인의 경험, 선임자의 조언 등을 통해 연료량을 결정하고 있다.
국내 LCC A 항공사의 대구공항발 일본 3개 노선(후쿠오카, 간사이, 나리타) 1,736편의 비행자료를 분석한 결과 평균 재량연료 탑재량은 874kg이었고 96.7% (1,680편)는 법정연료로 운항하였으며 3.3% (56편)만이 재량연료를 사용한 것으로 나타났다. 이는 사용하지 않는 재량연료 탑재로 인한 항공기 중량 증가로 추가적인 연료 소모를 발생시킨다고 볼 수 있다.
본 연구는 LCC 항공사 중 하나인 A 항공사(전 기종 Beoing 737-800)의 2017년 2월부터 2018년 9월까지의 대구공항 발 일본 3개 노선(후쿠오카, 간사이, 나리타)을 대상으로 첫째, 운항관리사가 재량연료량 결정 시 가장 중요하게 고려하는 요소를 알아보기 위하여 선행연구 참고 및 국내 운항관리사들을 대상으로 설문조사를 실시하였다. 둘째, FAA 및 EASA에서 제시한 Safety Analysis and Assessment의 발생확률을 참고하여 합리적인 재량연료량을 분석 후 이에 따른 노선별 연료 절감 예측비용을 정량적으로 나타내었다.
선행연구
Trujillo(1996)는 조종사와 운항관리사가 재량연료 탑재 시 고려요소들을 알아보고자 조종사와 운항관리사들을 대상으로 설문조사를 실시한 결과 58%가 기상을 고려한다는 것을 밝혀냈다. Gregor(2015)는 항공기 연료관리를 위해 다양한 요소(기상, 항공교통 흐름, 항로 거리 등)들을 포함한 모델 개발을 통하여 Final reserve fuel과 Fuel starvation의 가능성을 예측할 수 있을 것이라 하였다. Yoo(2014)는 목적지 공항의 기상예보(시정, 일기현상 중 강수, 안개, 뇌우)에 따른 재량연료 탑재 사유의 타당성을 알아보았다. 그 결과, 계획보다 연료가 부족했던 운항편들의 경우 재량연료 사용량과 악기상과의 상관계수가 상당히 높은 수치를 보였음을 분석하였다. Ryerson et al.(2015)는 조종사와 운항관리사가 만약을 대비하여 사용하지 않는 과도한 연료를 탑재하고 있다고 하였다. 이는 항공기 중량을 증가시켜 불필요한 연료를 더 사용하고 있고 이를 1갤런 당 3.2달러로 환산할 경우 1년에 223백만 달러를 절약할 수 있을 것으로 예측하였다. Yoo et al.(2017)는 인천 방콕 노선을 운항한 B777 항공기들의 연료 소모 및 탑재 자료에 대하여 정량적인 접근을 통해 충분한 안전 수준을 유지하면서 연료 탑재량을 어느 수준까지 감소시킬 수 있는지, 그리고 안전에 저해되지 않는 범위 내에서의 연료 탑재량 감소를 통해 얻을 수 있는 연료량 및 이산화탄소 배출량 감소 효과를 무게 인자와 연비손실 계산 방법을 적용해 산출하였다. Chang(2018)은 몬테카를로 분석을 통해 최적화된 모델을 수립하여 재량연료의 적정량을 제시함으로써 조종사 및 운항관리의 의사결정에 참고할 수 있도록 하였다. Kang et al.(2018) 또한 연료탑재를 하고 있는 운항관리사들이 예측불가능한 상황에 대비하기 위하여 필요한 연료량 이상을 탑재하고 있다고 하였으며 미국의 주요 6개 항공사를 대상으로 사용하지 않는 연료량(reserve fuel 제외)을 싣고 다님에 따른 추가적인 연료 사용 즉, CTC (Cost To Carry)를 계산한 결과 2013년 기준 930백만 달러의 추가 비용이 들었다고 예측했다.
용어설명
1. 항공기 연료의 정의
운항을 위한 항공기 연료의 정의는 MOLIT(2017)에 따라 Table 1과 같다.
Table 1. Aircraft fuel segments
FOD (Fuel On Destination)란 목적지 공항 착륙 시 Rampout fuel에서 Taxi fuel, Trip fuel을 사용하였을 때의 예상 연료량을 말한다(Equation 1 참조). 일반적으로 운항관리사는 비정상 상황 시 항공기가 목적지 공항에 착륙할 때의 예상 연료를 FOD와 비교하여 회항 등을 결정한다.
| $$FOD=Rampout\;Fuel-Taxi\;Fuel-Trip\;Fuel$$ | (1) |
일반적으로 항공기 연료 사용 순서는 Rampout fuel에서 Taxi fuel, Trip fuel, Contingency fuel, Discretionary fuel을 사용한다.
2. 기상예보(TAF)의 정의
Aviation Meteorological Office(2015)에서 TAF (Terminal Aerodrome Forecasts)는 일정기간(보통 6시간에서 30시간) 동안 공항에서 예상되는 우세한 기상현상에 대하여 국제적으로 합의된 부호를 사용하여 서술하는 것을 말하며 국제공항 기준 일 4회(05, 11, 17, 23 UTC) 발표한다. 다만 항공기 운항 상황을 고려하여 필요한 경우에는 공항 예보의 발표시각 및 유효시간을 조정할 수 있다. 공항 예보는 WMO No 306 Manual on Codes, FM 51-XII TAF ICAO ANNEX3, Appendix 5, Table A5-1 형식에 의해 발표하며, 항공고정통신망을 통해 국내 ‧ 외로 교환한다.
TAF의 구성요소는 다양하지만 본 연구에서 사용한 변수들은 Table 2와 같다.
Table 2. TAF explanation of terminology
Table 2에서와 같이 Wind, Visibility, Ceiling을 제외한 요소들을 일기 현상(present weather)이라고 부르며 Precipitation (RA, DZ, SN, GS)은 Table 3과 같이 강도(intensive)를 나타낸다.
Table 3. TAF explanation of intensity
| Intensive | Description |
| Light | - |
| Moderate | No remark |
| Heavy | + |
3. Safety Analysis and Assessment의 정의
FAA의 Advisory Circular 23(2019)와 EASA의 CS-25(2012)에서는 발생확률에 따른 심각도를 Table 4와 같이 정의하고 있다. 조종사는 비행 중 지속적으로 남은 연료량(remaining fuel)을 체크하고 연료 부족 시 즉시 주변 공항으로 회항하도록 법에서 규정되어 있기 때문에 본 연구에서는 연료 부족으로 인한 사상자가 발생하지 않고 조종사의 업무량(work load)만이 증가한다고 가정하였다. 따라서 Table 5에서와 같이 심각도 Minor에 따른 발생확률 10-3을기준으로 합리적인 재량연료량을 분석하였다.
Table 4. Failure condition classifications
Table 5. Relationship between probability and severity of failure condition
연구방법론
1. 기상예보와 재량연료량과의 다중회귀분석
국내 FSC 1곳, LCC 2곳의 운항관리사 19명(FSC 6명, LCC 13명)을 대상으로 재량연료 탑재 시 고려요소에 대한 설문조사 결과 항로 및 목적지 기상 63.2%, 공항 및 항로 혼잡 21.1%, 조종사 요청 10.5%, 기타 5.3% 순으로 나타났다. 설문조사 결과를 근거로 재량연료 탑재량과 항로 및 목적지 공항 TAF의 상관관계를 분석하고자 하였으나 모든 편의 항로기상 자료를 분석하는데 어려움이 있어 목적지 공항 TAF를 이용하여 Table 6과 같이 종속변수와 독립변수들을 정의하였다.
Table 6. Variable data description
노선별 재량연료 탑재량은 2017년 2월부터 2018년 9월까지 A항공사(전 기종 Boeing 737-800)의 대구공항발 1,736편(후쿠오카공항 537편, 간사이공항 도착 706편, 나리타공항 493편)의 운항데이터를 사용하였다. 1,736편의 평균 재량연료 탑재량은 874kg이었고 범위는 300kg부터 4,000kg까지 탑재한 것으로 나타났으며 표준편차는 540kg이었다.
목적지 공항 TAF에 따른 재량연료 탑재량과의 다중회귀분석을 실시한 결과는 Table 7과 같다.
Table 7. Results of the regression analysis
다중회귀분석 결과(Table 7) R2 값은 62.0%, R2 adjusted는 61.7%로 나타났다. 독립변수 중 FOG, Snow_light, Hail_light, Hail_moderate는 P값을 충족시키지 못하여 제거 후 분석결과는 Table 8과 같다.
Table 8. Analyzing results after removing variables
P값을 충족시키지 못하는 변수들을 제거한 다중회귀분석 결과(Table 8) R2 값은 62.0%, R2 adjusted는 61.7%로 나타났다. Table 8과 같이 바람의 세기가 강하고 일기현상(present weather)이 있을 때 재량연료 탑재량이 증가하는 것으로 나타났고 시정과 운고가 높을수록 재량연료 탑재량이 감소하는 것으로 나타났다.
2. 경제적인 재량연료 탑재량 분석
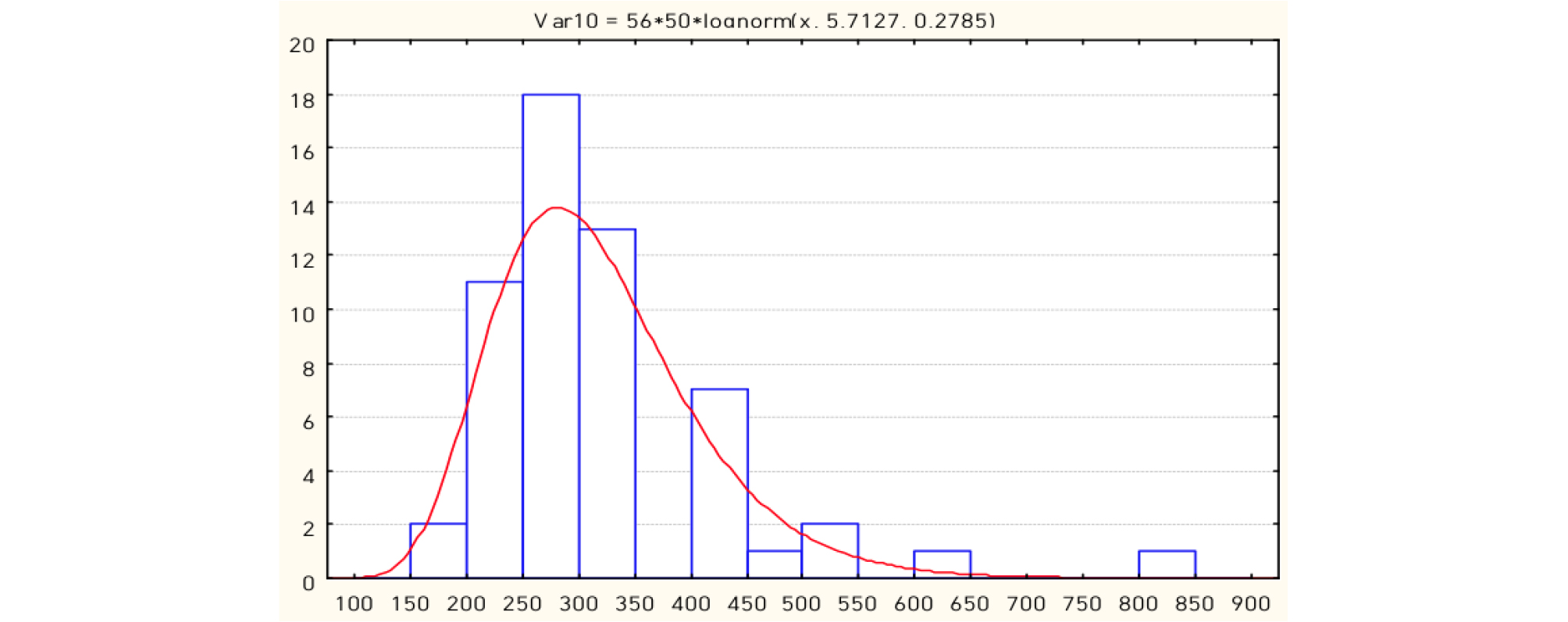
총 1,736편 중 56편이 법정연료(trip fuel, contingency fuel) 사용 후 재량연료를 사용한 것으로 나타났고 사용범위는 1kg에서 750kg이었다. 따라서 합리적인 재량연료 탑재량을 도출하고자 다음과 같은 절차를 통하여 검증하였다. 선행연구 Yoo et al.(2017)에서는 재량연료 탑재량을 계산함에 있어 정규분포를 가정하고 발생 확률(10-3, 10-5, 10-7, 10-9)에 따른 탑재량을 도출하였으나 본 연구에서는 실제 재량연료 탑재량 데이터(n=56)를 가지고 분포 모형을 추정 후 발생 확률(10-3, 10-5, 10-7, 10-9)에 해당하는 재량연료 탑재량을 계산하였다. 이를 위해 첫째, 표본 데이터 n=56을 가지고 분포 모형을 분석한 결과 Figure 1에서 보는 바와 같이 대수 정규분포(log-normal distribution) 모형을 하는 것으로 분석되었다. 둘째, x2 적합도 검증을 통해 실제 데이터가 대수 정규분포를 따르는지를 검증하였다. 셋째, 검증 결과 대수 정규분포 모형이 적합한 것으로 나타남에 따라 동 분포를 이용하여 위험이 발생할 수 있는 확률 10-3, 10-5, 10-7, 10-9에 해당하는 재량연료 탑재량을 도출하였다.
1) 대수정규분포 모형의 적합도 검증
(1) 대수정규분포 확률밀도함수
Figure 3에서 볼 때 정적편포(positive skew)되는 형태를 띠고 있으므로 일반적인 정규분포 보다는 대수정규분포의 형태가 적합한 것으로 분석된다. 일반적으로 확률변수 x에 대한 대수정규분포의 확률밀도함수식(Hossack et al., 1999)은 Equation 2와 같다.
| $$f_X(x)=\frac1{\sigma x\sqrt{2\pi}}e^{-\frac12{(\frac{\ln x-\mu}\sigma)}^2},\;x>0$$ | (2) |
Equation 2의 평균은 Equation 3, 분산은 Equation 4와 같다.
| $$평균=e^{\mu+\frac12\sigma^2}$$ | (3) |
| $$분산=e^{(2\mu+\sigma^2)}\left[e^{\sigma^2}-1\right]$$ | (4) |
(2) x2적합도 검증방법
확률변수 X1, X2, … , Xn가 가정된 분포(대수 정규분포)에 적합한가를 검정하는 것을 적합도 검증(Test for Goodness of Fit)이라고 한다. 이와 같은 적합도 검증 중의 하나가 칼 피어슨(K. Pearson)에 의해 고안된 “적합도를 위한 피어슨의 x2통계량”이다. 다시 말해 x2 통계량이 적으면 적을수록 확률변수 Xi가 가정된 분포에 잘 적합하다고 할 수 있는데 일반적인 검증절차는 다음과 같다.
첫째, 귀무가설(null hypothesis)을 설정한다. 즉, H0:P1=P10, P2=P20, … , Pk=Pk00
둘째, 귀무가설 하에서의 검정 통계량은 Equation 5와 같이 계산한다. (O는 관찰값, E는 기댓값)
| $$\chi^2=\sum_{i=1}^k\frac{{(n_i-n\cdot P_{i0})}^2}{n\cdot P_{i0}}=\sum\frac{{(O-E)}^2}E$$ | (5) |
셋째, 관찰건수 n이 크면 x2는 자유도(degree of freedom)가 k−1인 x2분포를 한다.
넷째, 기각역 α를 설정한다. 즉, 유의수준(critical region) α에서 가 되는 를 찾는다. 이때 자유도는 k−1이 된다.
위와 같은 검증절차에 의해 구한 검정통계량 x2값이 보다 크면 귀무가설은 기각된다. 즉, 확률변수 Xi가 가정된 분포(대수정규분포)에 잘 적합지 못하다고 볼 수 있다.
(3) 실제 데이터(n=56)에 의한 대수정규분포의 적합도(x2)검증
n=56의 데이터를 이용해서 표본평균()과 표본표준편차()을 구하면 Equation 6, Equation 7과 같다.
| $$\overline x=\frac1{56}(801+610+\cdots+200)=314.6563$$ | (6) |
| $$s^2=\frac1{56-1}\lbrack{(801-314.6563)}^2+{(610-314.6563)}^2+\cdots+{(200-314.6563)}^2)\rbrack=7,9798.5984$$ | (7) |
Equation 3과 Equation 4에서
| $$e^{\mu+\frac12\sigma^2}=314.6563$$ | (3)‘ |
이고
| $$e^{(2\mu+\sigma^2)}\lbrack e^{\sigma^2}-1\rbrack=7,979.5984$$ | (4)‘ |
가 된다. 여기서, Equation 3‘을 자승하면 이 된다. 이를 Equation 4‘에 대입해서 σ2를 계산하면 다음과 같다. 이 되므로 이 되고 이를 Equation 3‘에 대입해서 계산한 결과는 Equation 8과 같다.
| $$e^{\mu+\frac12\times0.0775}=314.6563$$ | (8) |
Equation 8에 따라 이 된다. 따라서 귀무가설과 대립가설은 다음과 같이 설정된다.
귀무가설(H0): 모집단의 분포는 , 인 대수정규분포를 한다. 대립가설(H1): 모집단의 분포를 , 인 대수정규분포를 하지 않는다.
위 「(2) x2적합도 검증방법」에 따라 x2 검정통계량을 구하면 Table 9와 같다. 예를 들어, 재량 탑재연료량의 크기가 인 기대건수 (E)를 계산하기 위해 Equation 9와 같이 을 계산하면
| $$f_x(x)=\int_{200}^{400}\frac1{x\sqrt{2\pi}(0.2785)}e^{-\frac{(\ln x-5.7127)}{2\cdot{(0.2785)}^2}}dx$$ | (9) |
가 되고 이를 누적정규분포함수(cumulative normal distribution)1)식은 Equation 10과 같다.
따라서 재량 탑재연료량의 구간()의 기대건수(E)는 56×0.771=43이 된다. 동일한 방법에 의해 각 구간별 기대건수를 구하면 Table 9와 같다.
Table 9. x2 test statistic
또한 재량 탑재연료량 분포에서 자유도는 (범주의 수-1)-(추정된 모수의 수)가 된다. 따라서 추정된 모수(, )가 2개이므로 자유도 (5-1)-(2)=2가 된다. 결과적으로 Table 9의 x2 검증통계량=1.13이 보다 적게 되므로 n=56개의 재량연료 데이터는 평균이 5.7127이고 표준편차가 0.2785인 대수정규분포를 따른다고 볼 수 있다.
2) 위험발생 가능성 10-3, 10-5, 10-7, 10-9에 대한 재량연료의 계산
n=56개의 재량연료 탑재 데이터는 , 인 대수정규분포를 하므로 위험발생가능성 10-3=0.001에 대한 재량연료 탑재량 D는 Equation 11과 같이 계산된다. 여기서, fX(x)는 대수정규분포함수이다.
| $$F(D)=\int_D^\infty f_X(x)dx=0.001$$ | (11) |
이를 누적정규분포(cumulative normal distribution) Φ(x)로 쓰면 Equation 12와 같다(Strauss, 1975).
| $$F(D)=1-\lbrack\Phi(\frac{\ln D-\widehat\mu}{\widehat\sigma})\rbrack=0.001$$ | (12) |
, 이므로 이를 Equation 13에 대입하면 실패확률 10-3=0.001에 해당하는 재량 탑재연료는 다음과 같이 계산된다.
| $$\Phi(\frac{\ln D-5.7127}{0.2785})=0.9990$$ | (13) |
따라서 누적정규분포표에서 99.9%에 해당하는 가 되므로 D=715이 된다. 동일한 방법에 의해 계산된 발생확률별 재량연료 탑재량은 Table 10과 같다.
Table 10. Discretionary fuel size by failure condition
| Failure condition | 10-3 | 10-5 | 10-7 | 10-9 |
| Discretionary fuel | 715kg | 992kg | 1,287kg | 1,608kg |
결론
본 연구는 목적지 공항 TAF와 재량연료 탑재량과의 상관관계와 합리적인 재량연료 참조값을 도출하기 위하여 대구공항발 3개의 일본 노선 1,736편을 대상으로 연구를 실시하였다. 목적지 공항 TAF와 재량연료 탑재량과의 상관관계를 알아보고자 다중회귀분석을 실시한 결과 운항관리사 61.7% 정도가 비행계획서 작성 시 목적지 공항 TAF를 참고한다는 것을 알 수 있었다. 하지만 재량연료를 사용한 운항편은 56편으로 지금까지 불필요한 연료를 탑재하고 다님으로써 항공기 중량증가 및 Trip fuel을 증가시켰다고 볼 수 있다. 따라서 연료비용을 절감하기 위해 FAA 및 EASA에서 제시한 위험 발생확률에 따른 합리적인 재량연료량을 분석한 결과 715kg (10-3 발생확률 기준)을 도출하였고 도출한 값을 탑재하였을 때 예상 연료절감량을 분석하고자 Airbus사의 Navblue라는 비행계획 프로그램을 사용하여 1,000kg당 무게 증감 시 노선별 평균 Trip fuel의 변동량을 구하였다(Table 11 참조).
Table 11. Fuel saving cost according to 10-3 failure condition
1,736편의 노선별 실제 평균 재량연료 탑재량과 분석한 재량연료량을 탑재하였을 때의 예상 연료절감량 및 연료절감 비용을 분석한 결과는 Table 11과 같다.
Table 11과 같이 10-3의 분석값을 기준으로 재량연료를 탑재했을 경우 후쿠오카 노선은 편당 0.95달러의 연료절감 효과를 예상할 수 있었고 간사이 노선은 편당 3.43달러의 연료절감 효과를 예상할 수 있었으며 나리타 노선의 경우 편당 약 12.82달러의 절감효과를 예상할 수 있었다.
1,736편은 A항공사의 전체 편수 중 일부라는 점을 고려한다면 위와 같은 방식을 통해 연간 억 단위(2017년 국제선 17,023편 기준)의 연료비용 절감효과를 기대할 수 있을 것으로 예상되었다. 다만, 본 연구의 결과는 단일 기종(Boeing 737-800)을 운영하고 있는 단일 항공사의 데이터라는 한계가 있어 향후 다양한 항공사의 데이터와 기종, 노선의 세부화 등을 통한 분석이 필요할 것으로 보여진다.
유가와 환율의 변동은 불규칙적이고 변동 폭이 매우 크기 때문에 항공사는 연료비용 증가에 미리 대비해야 할 것이다. 이처럼 지속해서 연료 절감을 위해 노력한다면 항공사의 지속적인 발전을 기대할 수 있을 것이다.
1).