서론
1. 연구의 배경 및 선행연구
오늘날 도시부 인구의 증가와 도시 중심적인 생활패턴은 교통 혼잡 및 사고와 같은 현대사회의 현안을 증가시키고 있으며, 이러한 사회 현안을 해결하기 위하여 기존 도로상에서 지능형교통시스템(Intelligent Transportation System, ITS)을 구현하려는 수많은 시도가 이어져 왔다. 현재 ITS 분야에서 차량 운전자와 교통시스템 관리자 모두에게 가장 널리 활용되는 정보는 개별 도로의 실시간 통행시간(travel time) 정보이다. 첨단여행자정보시스템(Advanced Traveler Information System, ATIS) 기반의 통행시간 정보 실시간 업데이트를 통하여 차량 운전자들의 혼잡 도로 회피를 유도할 수 있으며(Yang and Zhou, 2017), 교통관리자들은 실시간 통행시간 정보 분석을 통하여 첨단교통관리시스템(Advanced Traffic Management System, ATMS) 기반의 다양한 교통제어 전략을 적용하여 교통 혼잡을 감소시킬 수 있다(Kim et al., 2019). 또한, 버스정보시스템(Bus Information System, BIS)을 기반으로 대중교통 운영 및 이용에 대한 효율적인 의사결정도 가능하다(Lee et al., 2017). 따라서 실시간으로 개별 도로의 통행시간을 보다 정확하게 추정하는 기술에 대한 연구는 향후 ITS 구현 및 확산을 위하여 매우 중요한 과업이다.
통행시간 정보는 간접 또는 직접적으로 수집될 수 있다. 간접적인 방법은 일반적으로 루프검지기(loop detector), 카메라 및 레이더와 같은 도로변의 지점센서로 측정한 교통량 및 지점속도(spot speed)를 기반으로 일정 도로구간의 통행시간을 추정하며(Tang et al., 2016a; Gan et al., 2017; Lu and Dong, 2018), 직접적인 방법은 자동차량인식장치(Automatic Vehicle Identification, AVI) 기술의 일환인 노변기지국(Road Side Unit, RSU)을 통하여 도로구간의 통행시간을 측정하는 것이다(Tam and Lam, 2008). 내비게이션 단말기 또는 스마트폰이 장착된 probe 차량에서 수집되는 GPS 정보를 활용하는 것 또한 통행시간을 직접적으로 측정하는 방법이며, 이는 스마트 기기들이 보편화됨에 따라서 비교적 적용가능한 공간적 범위가 넓고 운영비용이 적게 소요되어 오늘날 널리 사용되고 있는 방법이다(Shi et al., 2017; Cheng et al., 2019).
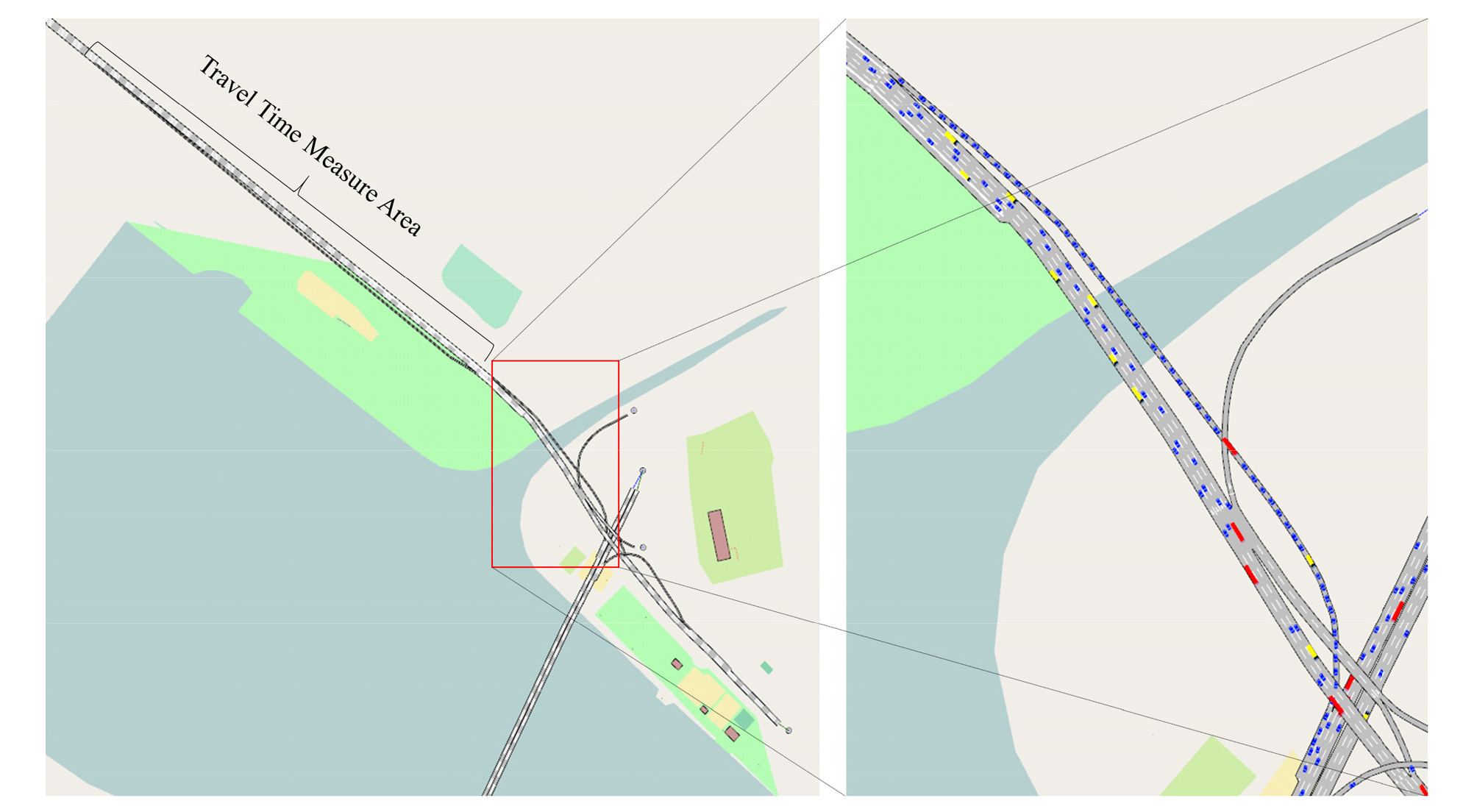
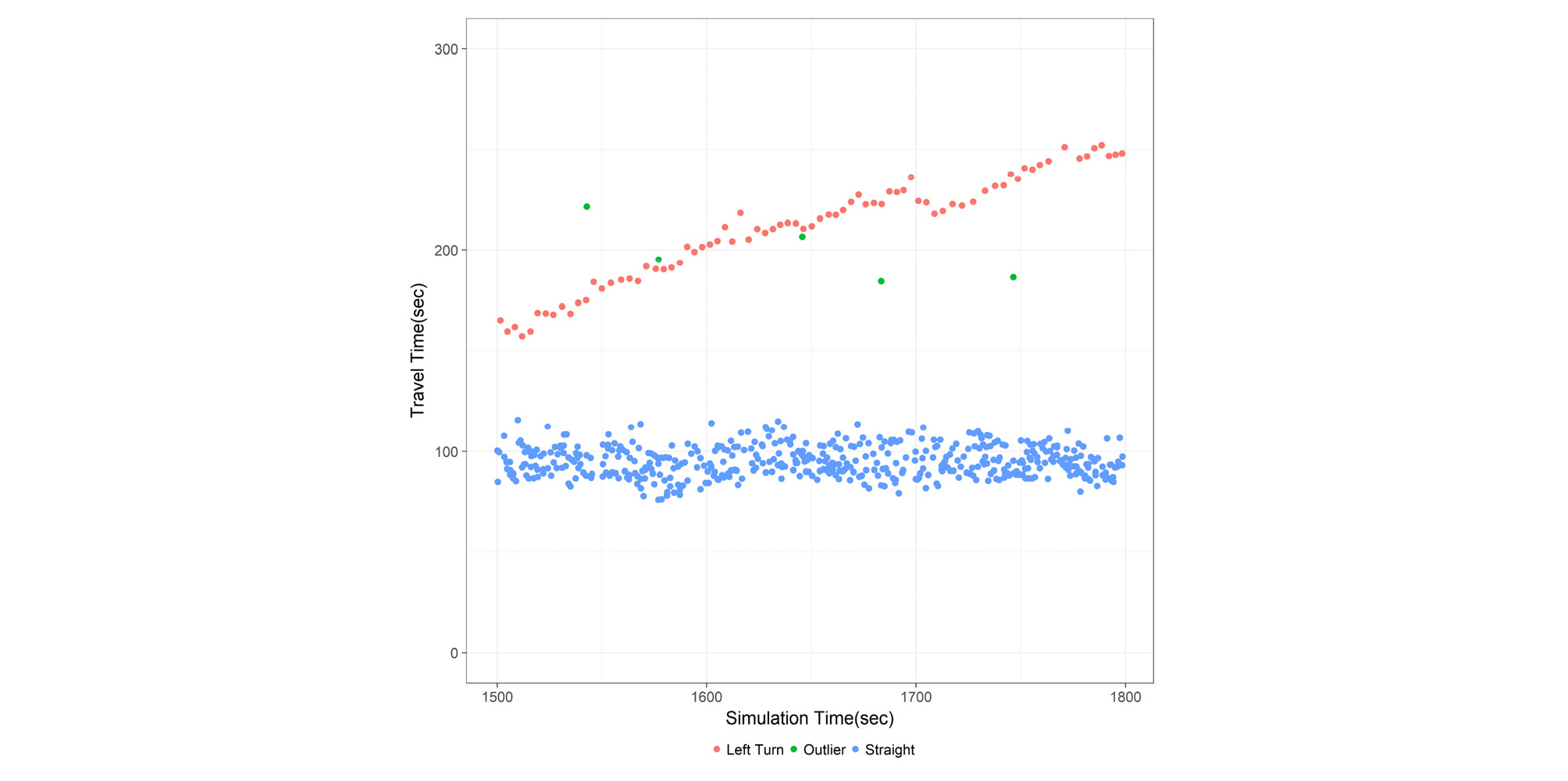
Probe 차량을 활용하여 통행시간을 추정하는 방법에는 크게 3가지 주요 문제가 있다. 첫 번째 문제는 장비장착차량비율(Market Penetration Rate, MPR)이다. 통행시간 추정은 일반적으로 일정구간을 통과한 다수 차량들의 통행시간 분포의 통계적 분석을 통하여 이루어지나, probe 차량의 수가 필요 이하로 적으면 추정 정확도가 저하되기 때문이다. 이러한 문제를 배경으로 통행시간을 추정함에 있어 MPR의 최소요건을 조사하거나(Cetin et al., 2005; Bolbol et al., 2012), 낮은 MPR 조건에서도 통행시간 추정 정확도를 높일 수 있는 방법 개발에 집중한 사례가 있으며(Jenelius and Koutsopoulos, 2013; Wang et al., 2014; Tang et al., 2016b), 통행시간 수집의 최적 간격에 대한 연구 사례도 있다(Park and Kim, 2017). 두 번째 문제는 수집된 데이터에 이상치(outlier)가 관찰된다는 점이다. 이상치는 일정 도로구간에서 차량이 주행 중 일시적으로 갓길에 정차하거나 유턴을 시행할 때 발생할 수 있으며, 통신장비 자체의 문제로 인한 측정 오류 등 다양한 요인으로 인하여 발생할 수 있다. 따라서 수집된 통행시간 데이터의 이상치 제거를 위한 다수의 기존 연구 사례도 있다(Moghaddam and Hellinga, 2013; Shaikh and Kitagawa, 2014; Jang, 2016; Park and Kim, 2018). 세 번째 문제는 단일 도로 구간에 다른 종류의 교통류(traffic stream)가 존재할 경우 발생한다. 특히 고속도로 분기지점에서는 Figure 1과 같이 각 차량의 진행방향에 대한 수요량의 불일치가 클 경우 해당 분기지점의 상류부에서 병목현상이 발생하며, 이를 분기지점 병목현상(diverge bottleneck)이라 부른다(Munoz and Daganzo, 2002; Rudjanakanoknad, 2012). 이러한 현상이 발생하였을 경우에는 동일 구간이라도 각 차량의 진행방향별로 통행시간이 크게 상이할 수 있으며, 이에 대한 정확한 분석 및 추정이 이루어지지 않는다면, ATIS 또는 ATMS 사용자들에게 부정확한 정보가 전달되어 비효율적인 ITS 운영의 가능성이 크다. 단적인 예로 Figure 2는 Figure 1의 도로를 교통 시뮬레이션으로 구현하고, 분기지점 병목현상이 발생하는 구간의 차량별 통행시간을 나타낸 것이다. 해당 구간의 대표 통행시간을 통상적인 방법으로 전체 차량의 평균을 내어 운전자들에게 전달한다면, 이 통행시간은 진출램프(off-ramp)로 진출하려는 대기열의 실제 통행시간(Figure 2의 붉은색 데이터 포인트)보다 낮으며, 이러한 잘못된 정보의 전달은 진출대기열의 차량들에게 혼잡도로 회피의 기회를 부여하지 못하는 계기가 된다. 이에 따라 단일 도로구간에 다른 종류의 교통류가 존재할 때, 각 진행방향 교통류별로 통행시간을 별도로 추정하는 방법이 필요하다.
앞서 언급한 세 번째 문제 해결을 위하여 노력을 기울인 몇 가지 연구 사례가 있다(Ban et al., 2009; Jenelius and Koutsopoulos, 2013; Liu et al., 2013; Shatnawi et al., 2018). 기존의 연구들은 주로 도로의 분기지점에서의 지연시간(delay)을 분기지점 직전 상류부의 통행시간과 별도로 추정하는 방식을 가진다(Jenelius and Koutsopoulos, 2013). 그러나 분기지점 지연시간과 상류부 통행시간을 다시 결합하여 통행시간을 단일 값으로 표현하기 때문에 한계가 있다. 이러한 방법은 교통운영 및 제어 시스템에는 활용될 수는 있으나, 차량 운전자를 위한 경로안내시스템 개선에는 적합하지 않다. 이러한 문제를 개선하기 위하여 최근의 몇 가지 연구에서는 개별 교통류의 통행시간을 별도로 추정하는 방법을 연구하였다(Wang et al., 2016; Shi et al., 2017). 이들이 제시한 방법은 추정 정확도 측면에서는 성공적이었으나, 수많은 GPS 지점들을 기반으로 다수 차량의 주행방향과 궤적들을 지속적으로 추적해야 하는 복잡하면서도 시간이 많이 소비되는 방법이며, 이에 따라 이들의 방법에는 실시간 구현 가능성이 배제되어 있다. 더욱 실용적인 솔루션의 관점에서는 입력 데이터와 통행시간 추정 방법은 단순성이 유지될 필요가 있다. 이러한 이유로 수많은 기존의 관련 연구들이 매초마다 차량의 미세한 위치를 미세하게 추적하는 방법 대신, 일정 도로구간을 통과한 차량들의 진출입 타임스탬프(timestamp) 데이터를 단순화하여 통행시간 분포에 대한 통계적 분석을 사용하는 방법을 고수하고 있다(Cetin et al., 2005; Ban et al., 2010; Jang, 2016).
2. 연구의 목적
통행시간 추정관련 연구 배경에 따라서 동일 도로구간 개별 교통류의 통행시간을 별도로 추정함에 있어 타임스태프 데이터와 같은 단순화된 데이터를 활용하는 실용적인 방법 개발이 필요하다. 이에 본 연구의 목적은 타임스탬프 데이터를 활용하여, 도로상 분기지점에 의하여 상류부 단일 도로구간에 서로 다른 종류의 교통류가 존재할 때 각 진행방향 교통류별로 통행시간을 별도로 추정하는 방법을 제시하는 것이다. 제시하는 방법은 ‘데이터 분기 감지’, ‘분기된 데이터 분류’, ‘데이터 이상치 제거’의 순차적인 3개의 단계로 구성된다. ‘데이터 분기 감지’에서는 진행 방향별 통행시간의 차이 발생 여부를 감지할 수 있는 통계적 분석 방법을 제시하며, ‘분기된 데이터 분류’에서는 통행시간 차이가 감지되었을 때 이를 각 방향별로 데이터를 분류할 수 있는 통계적 접근 방법을 제시한다. ‘데이터 이상치 제거’에서는 차량의 주행 중 정차와 같은 비정상적인 행태를 보이는 데이터를 제거하기 위하여 단순이동평균 기반의 분석 방법을 활용한다. 본 연구에서 제시하는 방법은 타임스태프 데이터와 같은 단순화된 데이터를 활용하여 실시간적 실용성을 추구함과 동시에, 통행시간 별도 추정의 정확도를 향상시키기 위하여 위 3단계 분석의 체계적인 구성을 새롭게 제시한다는 점에서 기존연구와 차별성이 있다. 본 연구에서 제시하는 방법의 통행시간 추정 성능을 조사하기 위해 각 단계별로 세부적인 분석을 수행하고자 하며, 다양한 데이터 수집 조건에서의 추정 성능을 실험하기 위하여 AIMSUN 마이크로 시뮬레이션 프로그램(AIMSUN, 2011)을 통한 데이터를 활용하고자 한다.
본 연구의 범위는 타임스탬프 데이터를 활용한 차량 진행방향별 통행시간 추정 방법의 초기 작업으로서 고속도로의 연속류 분기지점을 다루며, 추후 도시부 일반도로 교차로와 같은 단속류 지점으로 연구 범위를 확장시킬 예정이다.
본론
1. 연구방법론
타임스탬프 데이터를 기반으로 고속도로 분기지점 상류부에서 진행방향 교통류별 통행시간을 별도로 추정하는 방법의 전체 구성은 Figure 3과 같다. 단일 도로 구간에 대한 차량들의 진입 및 진출 시간들의 기록을 입력 데이터로 활용하며(Input 기능), 주어진 시간 간격마다(예: 매 5분) 수집된 입력 데이터를 기반으로 개별 차량들의 진출 및 진입 시간의 차이를 계산하여 해당 도로의 통행시간 값들에 대한 샘플링을 수행한다(Pre-processing 기능). 그 후, 샘플링이 완료된 데이터 포인트들에 통계 분석을 적용하여 직진방향 교통류(forward stream) 및 회전방향 교통류(turning stream)에 해당하는 데이터 포인트들로 분류한다(Travel Time Data Classification 기능). 고속도로에서는 진출램프방향 교통류(off-ramp stream)를 회전방향 교통류로 간주한다. 그리고 분류가 완료된 데이터 포인트들을 기반으로 해당 도로구간 내 각 진행방향별 교통류에 대한 통행시간을 별도로 추정한다(Output 기능).
본 연구에서는 Travel Time Data Classification 기능 구현 측면에서 세부 방법론 개발을 위한 다양한 분석을 수행함에 중점을 두고 있다. 해당 기능을 ‘데이터 분기 감지’, ‘분기된 데이터 분류’, ‘데이터 이상치 제거’의 순차적인 3개의 단계로 구성하여 제시하며, 각 단계에 대한 세부설명은 다음과 같다.
1) 데이터 분기 감지
첫 번째 단계인 ‘데이터 분기 감지’의 목적은 수집된 통행시간 분포(distribution)에서 데이터 분기(divergence) 발생 여부와 그 분기 정도가 유의한지 판단하는 것이다. Figure 2의 데이터 분포 중 희소 데이터(sparse data) 포인트들은(붉은색 및 녹색 데이터 포인트) 회전방향 교통류에 대한 상태 변화로 분석되어야 하지만, 전통적인 분포 분석의 관점(Jang, 2016)에서는 데이터 이상치로 간주되어 제거될 가능성이 높다. 따라서 희소 데이터 포인트들이 단순히 이상치인지 혹은 회전방향 교통류에 의한 영향인지를 감지할 수 있는 분석 방법이 필요하다.
일반적으로 데이터 분포의 산술평균(mean)과 중앙값(median)은 서로가 다른 수준의 통계적 유의성(statistical significance)을 표현한다. 산술평균을 활용한 통계적 표현은 작은 비율의 극단값(extreme values or outliers)들로 인하여 전체의 평균적 행태가 비교적 쉽게 왜곡되어(skewed) 표현될 수 있는 반면, 중앙값을 활용한 통계적 표현은 극단값들에 의해 크게 왜곡되지 않기 때문에 데이터 분포 내 극단값이 다소 많이 존재할 경우 이에 대한 분석에 유용하다. 따라서 통행시간을 추정함에 있어 데이터 극단값의 영향을 고려하기 위하여 산술평균과 중앙값의 특성을 비교하거나 결합하는 방법을 연구한 사례가 있다(Ban et al., 2010; Park and Kim, 2018; Cheng et al., 2019).
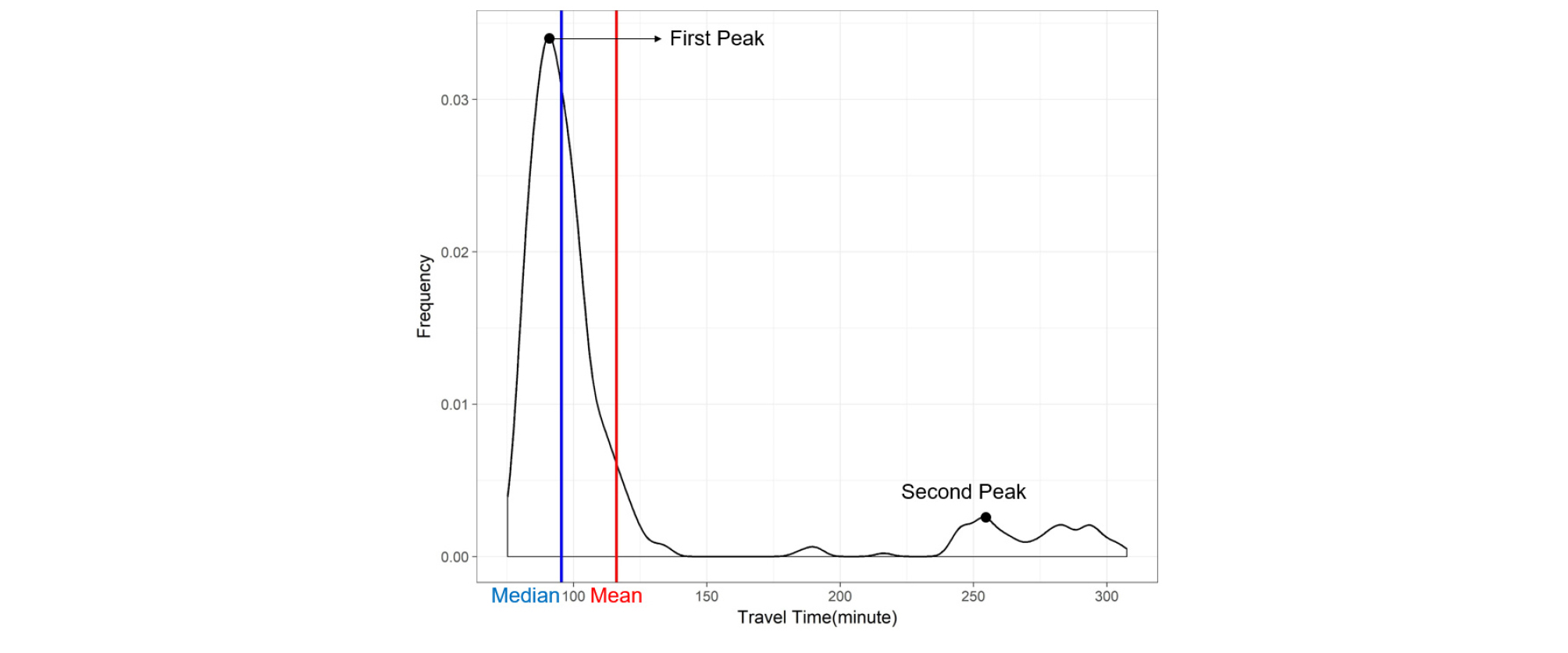
직진방향 및 회전방향 교통류 모두에 정체가 발생하지 않거나 또는 정체가 발생했을 경우에는 이 두 종류의 교통류는 동일한 교통상태를 공유하기 때문에 단일 교통류로 간주될 수 있다. 이 경우의 통행시간 히스토그램은 일반적으로 특정 왜도(skewness)를 가진 단봉(unimodal)의 형태를 가지며(Park and Kim, 2018), 왜도에 따라 산술평균과 중앙값의 차이가 있을 수는 있지만 그 차이의 정도는 크지 않다. 반면에, Figure 1과 같이 두 종류의 교통류 중 하나는 원활하고 다른 하나가 정체상태이면, Figure 4와 같이 통행시간 히스토그램은 2개의 피크(peak)가 존재하는 양봉(bimodal)의 형태를 가지게 된다. 특히, 원활한 교통류의 통행시간이 정체 교통류보다 낮기 때문에 두 개의 피크 중에 첫 번째(왼쪽) 피크에 해당되며, 또한 일반적으로 차량 통과비율이 더욱 높기 때문에 해당 피크는 정체 교통류의 피크보다 비교적 높아진다. 이 경우에 산술평균은 두 개의 피크 사이에 존재하며, 중앙값은 원활한 교통류에 해당하는 첫 번째 피크에 더욱 가깝게 존재하게 된다. 따라서 분포가 명확하게 분리된 양봉의 형태를 가질 때, 산술평균과 중앙값 차이의 양은 더욱 커지게 되며 유의하다 할 수 있다.
본 연구에서는 위와 같은 산술평균과 중앙값의 기본적인 특성을 활용하여 통행시간 분포의 분기 여부를 감지할 수 있는 방법을 제시한다. 통행시간 데이터의 분기를 감지하고, 분기된 희소 데이터가 이상치가 아닌 유의한 데이터임을 판단하기 위한 지수(index)인 xh(ti)를 Equation 1과 같이 제시하며, 해당 지수와 관련된 주요 변수에 대한 설명은 Table 1과 같다.
| $$x_h(t_i)=\lbrack T_h^{me}(t_i)-T_h^{md}(t_i)\rbrack/s_h(t_i)$$ | (1) |
해당 지수 xh(ti)는 표준편차에 대한 산술평균과 중앙값의 차이의 비율로 계산된다. 해당 지수의 값이 주어진 임계값보다 큰 경우, 분석 대상인 데이터 분포의 분기가 유의하다고 판단하며, 이 때 분기된 희소 데이터를 단순 이상치로 제거하지 않게 된다. 이러한 판단이 내려졌을 때 그 다음단계인 ‘분기된 데이터 분류’ 단계로 넘어가도록 설정된다. 해당 지수의 임계값은 모든 도로에 대하여 일반화된 값이 아니고 개별 도로의 특성에 따라 그 수치가 구간마다 다를 수 있으며, 이에 개별 도로구간의 xh 임계값을 찾기 위한 분석수행 내용을 본 논문의 본론 3장에서 제공한다.
Table 1. Description of variables
2) 분기된 데이터 분류
데이터의 분기가 감지되었을 때, 해당 데이터 포인트들은 차량들의 진행방향별 통행시간을 추정하는 데에 별도로 구분되어 활용되어야 하며, 이러한 필요성에 의하여 ‘분기된 데이터 분류’ 단계가 제시된다. 본 단계에서의 주요 초점은 샘플링된 통행시간 데이터 포인트들을 직진방향 또는 회전방향 교통류 그룹으로 구분하는 것이다. 특히, 이 단계에서 데이터의 실제 이상치 포인트들은 회전방향 교통류 그룹으로 구분될 것이며, 이들을 회전방향 교통류 그룹에서 제거하는 최종 과정은 다음 단계인 ‘데이터 이상치 제거’에서 시행된다.
본 단계에서의 주요 이슈는 데이터를 분류하는 방법에 있어서 항상 우월한 솔루션이 없다는 것이다. 데이터 분류의 성능은 활용되는 통계적 접근방법의 종류, 도로의 유형, 분석 데이터의 시간대, 샘플링된 데이터 비율 등과 같은 다양한 요인에 따라서 달라질 수 있기 때문이다. 따라서 본 연구에서는 데이터 분류 성능을 조사하고 합리적인 솔루션을 찾기 위하여 3가지 분류방법을 실험해보고자 한다.
(1) 분류 방법 1
본 방법은 산술평균인 Thme(ti)와 중앙값인 Thmd(ti)을 계산하고, 개별 데이터 포인트인 Thn(ti)의 값이 Thme(ti)에 더 가까우면 회전방향 교통류 그룹인 Gh1(ti)에 포함시키며(실제 이상치 포함), Thn(ti)의 값이 Thmd(ti)에 더 가까우면 직진방향 교통류 그룹인 Gh2(ti)에 포함시킨다. 본 방법에서 개별 데이터 포인트 Thn(ti)을 분류하는 조건식은 Equation 2 및 Equation 3과 같다.
| $$G_h^1(t_i)={T_h^n(t_i):\vert T_h^n(t_i)-T_h^{me}(t_i)\vert<\vert T_h^n(t_i)-T_h^{md}(t_i)\vert}$$ | (2) |
| $$G_h^2(t_i)=\{{T_h^n(t_i):\vert T_h^n(t_i)-T_h^{me}(t_i)\vert\geq\vert T_h^n(t_i)-T_h^{md}(t_i)\vert\}}$$ | (3) |
(2) 분류 방법 2
본 방법에서는 중앙값에 대한 고려가 없이, 평균값에서 특정 범위를 벗어난 데이터 포인트들은 다른 종류의 교통류 행태를 표현한다는 점을 가정하여, 산술평균인 Thme(ti)와 표준편차인 sh(ti)을 활용한다. 이 방법에서는 해당 특정 범위를 표준편차의 1.5배로 간주하며, 개별 데이터 포인트인 Thn(ti)의 값이 해당 범위를 벗어나면 회전방향 교통류 그룹인 Gh1(ti)에 포함시키며(실제 이상치 포함), Thn(ti)의 값이 그 범위 내에 있으면 직진방향 교통류 그룹인 Gh2(ti)에 포함시킨다. 본 방법에서 개별 데이터 포인트 Thn(ti)을 분류하는 조건식은 Equation 4 및 Equation 5와 같다.
| $$G_h^1(t_i)=\{{T_h^n(t_i):T_h^n(t_i)>T_h^{me}(t_i)+1.5s_h(t_i)\}}$$ | (4) |
| $$G_h^2(t_i)=\{{T_h^n(t_i):T_h^n(t_i)LEQT_h^{me}(t_i)+1.5s_h(t_i)\}}$$ | (5) |
해당 특정 범위를 표준편차의 2배로 설정하면 3시그마 규칙(three-sigma rule)에 의거하여 약 95%의 데이터 포인트들이 해당 범위 안에 포함되어 회전방향 교통류에 해당하는 데이터 포인트들에 대한 분류가 경시(underestimate)될 확률이 높다. 반대로, 해당 특정 범위를 표준편차의 1배로 설정하면 약 68%의 데이터 포인트들만 해당 범위 안에 포함되어 매우 배타적인(overestimate) 분류가 되며 직진방향 교통류에 해당하는 다수의 데이터 포인트들이 회전방향 교통류 그룹에 잘못 포함될 가능성이 높아진다. 따라서 본 연구에서는 해당 특정 범위를 표준편차의 1.5배로 설정한다.
(3) 분류 방법 3
본 방법은 국내 고속도로 시스템으로부터 수집된 데이터 이상치 제거에 현재 사용되고 있는 한국도로공사(Korea Expressway Corporation)의 방법(Jang, 2016)을 기반으로 제시된다. 해당 방법은 ITS 기반의 고속도로 데이터에 대한 경험적인(empirical) 분석을 바탕으로 제시되었으며, 통행시간 데이터 이상치 제거 측면에서 최근 10여 년간 신뢰성을 유지하고 있는 방법이다. 본 방법은 표준편차인 sh(ti)에 대한 산술평균 Thme(ti)의 비율을 편차계수(Coefficient of Variation, CV)로 정의하며, Table 2와 같이 각 CV의 조건에 따라서 데이터 이상치를 제거하게 된다. 본 연구에서는 위와 같은 한국도로공사의 데이터 이상치 제거 방법을 기반으로, 데이터 포인트 Thn(ti) 중 제거 대상인 포인트들을 회전방향 교통류 그룹인 Gh1(ti)에 포함시키며, 제거 대상이 아닌 포인트들을 직진방향 교통류 그룹인 Gh2(ti)에 포함시킨다.
Table 2. Outlier removal method of Korea Expressway Corporation
3) 데이터 이상치 제거
Figure 2에서와 같이, 데이터 분류과정에서 회전방향 교통류 그룹인 Gh1(ti)에 포함된 몇몇의 데이터 포인트들은 회전방향 교통류에 포함된 차량들이 아닌 실제 데이터 이상치일 수 있다. 데이터 이상치는 도로구간에서 차량이 주행 중 일시적으로 갓길에 정차할 때 발생할 수 있으며, 통신장비 자체의 문제로 인한 측정 오류 등 다양한 요인으로 인하여 발생할 수 있다. 따라서 이 세 번째 단계의 목적은 회전방향 교통류로 분류된 데이터 중 실제 데이터 이상치를 제거하여 통행시간 추정의 정확도를 향상시키기 위함이다.
본 연구에서는 회전방향 교통류 그룹인 Gh1(ti)에서 이상치를 제거하기 위하여 단순이동평균(Simple Moving Average, SMA)를 기반으로 하는 접근방법을 사용한다. Figure 2에서 현시하는 바와 같이, 분기된 희소 데이터 포인트들은 직진방향 교통류와는 달리 증가되는 추세를 보인다. 이는 상류부 진출램프의 차선으로부터 혼잡 충격파(shockwave)가 전파되기 때문이며, 해당 충격파의 전파속도는 시계열 통행시간 증가에 영향을 미친다. 이동평균은 이러한 시계열 이벤트에 대한 추세 분석에서 가장 유용한 방법 중 하나로 알려져 있다(Kumar and Vanajakshi, 2015).
회전방향 교통류 그룹인 Gh1(ti)의 개별 데이터 포인트들의 수를 M으로 정의하고 개별 데이터 포인트를 Thm(ti)로 정의한다(m=1,2,3, ..., M). 또한, Gh1(ti) 중 이동평균을 계산하는 데에 사용되는 부분집합의 데이터 포인트 수를 ah로 정의하며, 해당 부분집합의 시작점인 데이터 포인트를 k로 정의한다(k=1,2,3, ..., [M-ah+1]). 위의 정의들을 기반으로, 그룹 Gh1(ti)에서 부분집합의 단순이동평균을 phm(ti, ah, k)로 정의하며, 그에 대한 계산식은 Equation 6과 같다.
| $$p_h^m(t_i,\;a_h,\;k)=\frac1{a_h}\sum_{m=k}^{m=k+a_h-1}T_h^m(t_i)$$ | (6) |
여기서 개별 데이터 포인트 Thm(ti)을 실제 데이터 이상치로 분류하는 그룹을 Gh3(ti), 그리고 회전방향 교통류로 최종 분류하는 그룹을 Gh4(ti)이라 정의한다(Gh1(ti)=Gh3(ti)∪Gh4(ti)). 또한, shm(ti)을 Thm(ti)의 표준편차로 정의하며, yh를 표준편차와 관련하여 실제 이상치 제거 대상의 범위를 결정하는 상수로 정의한다. 이와 같은 정의들을 바탕으로, 개별 데이터 포인트 Thm(ti)의 값이 이동평균값에서 표준편차의 yh배수 범위를 벗어나면 실제 데이터 이상치 그룹인 Gh3(ti)로 포함시키고, 해당 값이 이동평균값에서 표준편차의 yh배수 범위 이내에 있으면 회전방향 교통류의 최종그룹인 Gh4(ti)에 포함시킨다. 본 단계에서 개별 데이터 포인트 Thm(ti)을 분류하는 조건식은 Equation 7 및 Equation 8과 같다.
| $$G_h^3(t_i)=\{T_h^m(t_i):T_h^m(t_i)>p_h^m(t_i,\;a_h,\;k)+y_h\cdot s_h^m(t_i)\}\;\;\cup\{T_h^m(t_i):T_h^m(t_i)<p_h^m(t_i,\;a_h,\;k)-y_h\cdot s_h^m(t_i)\}$$ | (7) |
| $$G_h^4(t_i)=\{{T_h^m(t_i):T_h^m(t_i)\leq p_h^m(t_i,\;a_h,\;k)+y_h\cdot s_h^m(t_i)\}}\;\cup\{{T_h^m(t_i):T_h^m(t_i)\geq p_h^m(t_i,\;a_h,\;k)-y_h\cdot s_h^m(t_i)\}}$$ | (8) |
이동평균 계산에 사용되는 샘플링 크기 ah와 이상치 제거대상 임계범위를 정하는 yh은 개별 도로의 특성에 따라 그 값이 구간 또는 교통 상황별로 다를 수 있으며, 이러한 속성들에 대한 적절한 값을 찾기 위한 분석수행 내용을 본 논문 본론 3장에서 제공한다.
2. 분석용 데이터 설명
본 연구에서 제시된 방법론을 분석하기 위해서는 도로 분기지점 병목현상으로 인하여 상류부에서 상이한 행태를 보이는 각 진행방향별 교통류 통행시간의 실제값(true value)을 확보하는 것이 필요하다. 본 연구의 방법론을 활용한 통행시간 추정 결과와 실제값의 비교를 통하여 제시된 방법의 추정 성능 분석이 가능하기 때문이다. 그러나 일반적으로 probe 차량으로부터 수집되는 실제 교통데이터는 도로구간 전체 차량들 중 일부 샘플링된 결과이므로 해당 도로 교통상황의 실제값으로 볼 수 없다. 따라서 본 연구에서는 실제값의 대체를 위하여 AIMSUN 마이크로 시뮬레이션 프로그램 기반의 시뮬레이션 데이터를 활용하였다(AIMSUN, 2011). 각 진행방향별 교통류 통행시간의 실제값(true value)을 확보하는 것은 100% 커넥티드 차량(connected car)의 시대가 오기 전까지는 현실적으로 어려운 실정이다. 따라서 마이크로 시뮬레이션을 통하여 수집되는 데이터와 비교를 통한 분석이 현재 적용할 수 있는 최상의 선택이라 할 수 있다. 물론, 시뮬레이션 데이터가 실제 교통현상을 얼마나 정확하게 반영할 수 있는지의 여부에 따라서 시뮬레이션 데이터 기반 분석에 대하여 논쟁의 여지가 있다. 그러나 AIMSUN은 교통 시뮬레이션 프로그램 중 가장 널리 활용되는 상용화 소프트웨어 중 하나로서 실제 교통현상을 잘 반영할 수 있음이 수차례 검증된 바 있으며(Lu et al., 2014), 이를 기반으로 교통예측 및 교통운영 솔루션 도출 등 다양한 분석 및 개발용 도구로 사용되고 있다. 따라서 본 연구에서는 AIMSUN 시뮬레이션 상 모든 차량의 데이터를 실제값으로 간주하여 분석을 수행한다.
Figure 1은 서울시 강변북로와 성산대교를 연결하는 분기점 부근 도로망을 시뮬레이션으로 구현한 그림이다. 해당 도로에는 일반적으로 통행수요가 많고, 한강의 남쪽으로 이동하려는 진출램프로의 수요가 특히 많은 지점이며, 해당 분기지점의 병목현상으로 인하여 강변북로 상류부 교통류에 영향을 미치는 경우가 빈번히 일어난다. 이를 시뮬레이션에서 구현하기 위하여 진출램프의 시작지점으로부터 1km 상류부를 ‘통행시간 측정 영역’으로 설정하였다.
시뮬레이션에서 차량들의 통행수요는 실제 첨두시간대(peak hour) 2시간 동안의 수요량과 유사하게 적용하였다. 시뮬레이션 구현 시간 동안 적용된 직진방향 및 회전방향의 통행수요는 Table 3에서 보여주며, 각 시간대별 진출램프에 대한 수요는 전체 수요의 1/3로 설정하였다. 실제 교통상황과 유사하게 구현하기 위하여 일반차량 외 트럭 및 버스의 통행수요도 전체 수요의 5%의 비율로 설정하였다. 해당 유형의 차량들은 일반차량보다 차체의 길이가 길고 자유통행속도(free flow speed)가 낮아 도로구간 통행시간의 편차를 구현하기 위하여 적용하였다. 이에 더불어 통행시간 데이터 이상치를 발생을 유도하기 위하여, 해당 지역 부근의 난지한강공원으로 진출입하는 특정 차량들도 적용하였다.
Table 3. Traffic demand of each stream direction over simulation time
| Simulation time (hh:mm) | 00:00-00:30 | 00:30-01:00 | 01:00-01:30 | 01:30-02:00 |
| Forward stream volume (veh/h) | 10850 | 10850 | 8920 | 4960 |
| Turning stream volume (veh/h) | 5425 | 5425 | 4460 | 2480 |
또한 제시된 방법론의 일반성(generality)을 보장하기 위하여, 시뮬레이션의 생성 시드(generation seed)를 변경해가면서 30번의 시뮬레이션을 반복 수행하였다. 생성 시드는 미리 정해진 도로망 형태 및 통행 수요 설정 안에서 개별 차량의 통행출발시간 및 경로를 매번 다르게 적용하는 효과를 내며, 이로 인하여 각 방향별 교통류의 통행시간 및 분기지점 병목현상의 유지 시간 등이 일정 범위 안에서 매번 상이한 결과가 나올 수 있다.
시뮬레이션을 구현하면서 통행시간 측정 영역을 통과하는 모든 차량들의 진출입 타임스탬프를 해당 구간 진출 차량들의 순서대로 매 5분마다 수집하였다. 5분단위로 수집한 전체 차량들의 통행시간 데이터는 MPR 100% 환경에서 수집된 데이터로 간주하며, MPR이 100% 보다 낮은 조건에서는 전체 차량들 중 MPR 비율에 맞추어서 무작위(random)로 샘플링을 수행한다. 이와 같이 probe 차량의 다양한 MPR 조건에 맞춘 데이터를 활용하여 본 연구에서 제시한 방법론의 성능을 분석하였다.
3. 분석결과
통행시간 데이터 분류 기능의 각 3개의 단계에 대한 분석은 Table 4의 혼동행렬(confusion matrix)을 기반으로 수행하였다. 해당 분석은 본 연구에서 제시한 방법을 기반으로 통행시간 데이터 포인트들을 각 그룹으로 구분하였을 때, 추정과 실제가 일치한 횟수와 그렇지 않은 경우의 횟수를 기반으로 해당 방법의 데이터 그룹 구분 성능을 평가하는 방법이다. 평가지표의 범주는 true positive (TP), false positive (FP), false negative (FN), true negative (TN)의 4개로 구분하였다.
Table 4. Confusion matrix
| Estimation | Actual result | |
| Positive | Negative | |
| Positive | True positive (TP) | False positive (FP) |
| Negative | False negative (FN) | True negative (TN) |
여기서 유의할 점은 4개의 평가지표 범주 각각의 의미가 본 연구에서 제시한 3개의 단계별 분석에서 다르다는 점이다. 단계별 성능 평가는 Equation 9의 TP의 비율(true positive rate, TPR)과 Equation 10의 TN의 비율(true negative rate, TNR)을 기반으로 수행되었으며, 각 단계에서의 TPR 및 TNR의 정확한 의미는 단계별 분석 내용에서 설명한다.
| $$\mathrm{True}\;\mathrm{positive}\;\mathrm{rate}\;(\mathrm{TPR})=\frac{TP}{TP+FN}$$ | (9) |
| $$\mathrm{True}\;\mathrm{negative}\;\mathrm{rate}\;(\mathrm{TNR})=\frac{TN}{FP+TN}$$ | (10) |
1) 데이터 분기 감지 분석
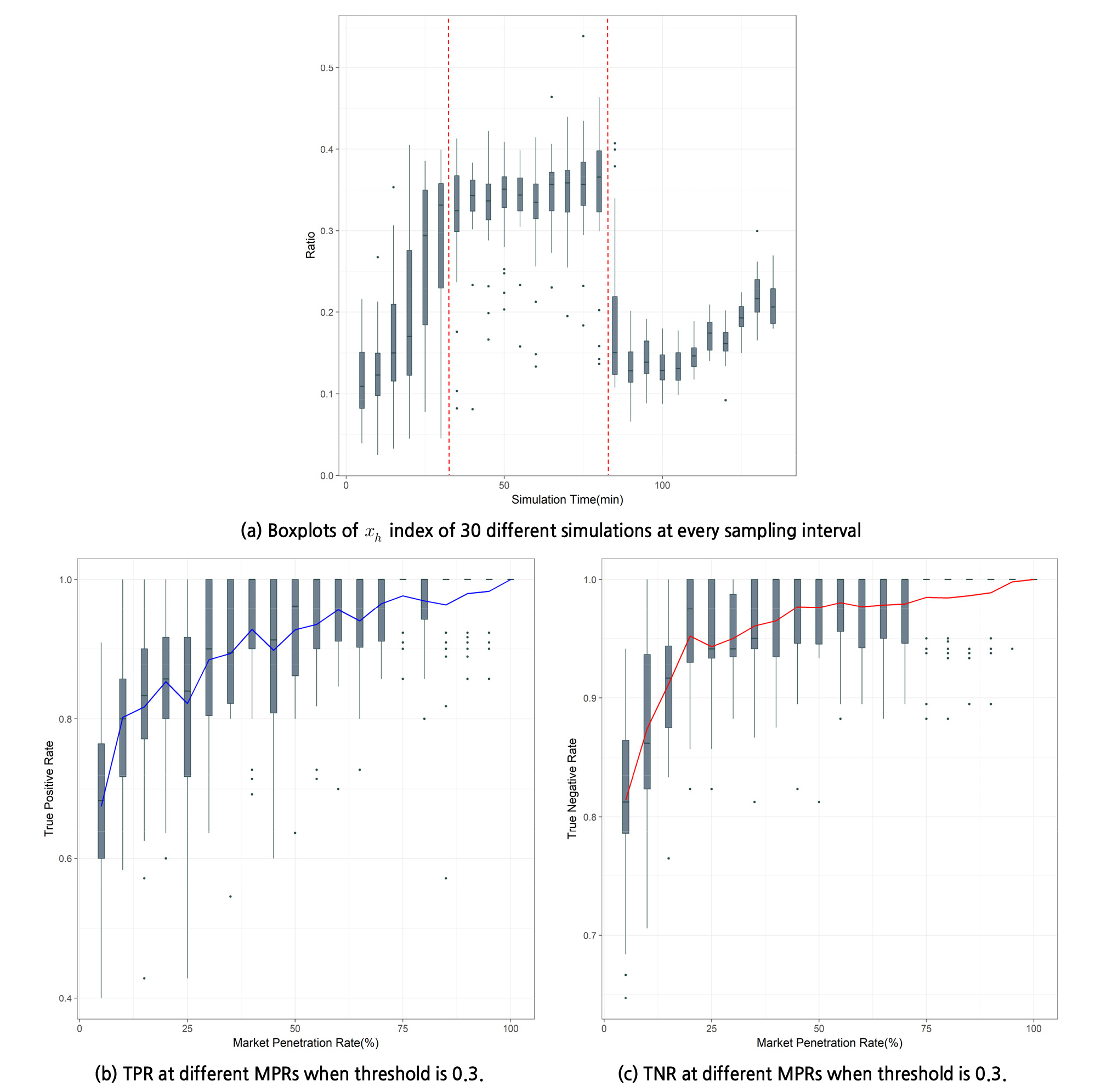
Figure 5(a)는 5분 단위로 수집된 전체 차량(MPR 100%)의 통행시간 데이터를 통해 Equation 1에서 정의된 xh 지수를 계산하고, 30번의 반복 시뮬레이션에서 각각 도출된 xh 지수들을 시뮬레이션 시간으로 구분하여 box plot으로 표출한 그래프이다. 그래프의 붉은색 점선은 시뮬레이션 교통상황 상 통행시간 데이터의 분기가 실제 발생했을 때의 시간 범위를 나타내며, 이 시간범위에서 xh 지수의 분포가 명확하게 증가된 변화를 보여준다. 해당 도로 구간에서 데이터 분기가 발생한 이 시간대의 xh 지수는 0.3보다 높은 것으로 결과가 나왔으며, 이에 본 연구에서는 해당 도로구간의 xh(ti)의 임계값을 0.3으로 설정하였다. 즉, ti 시점에 샘플링된 통행시간 데이터에서 xh(ti)>0.3이면 해당 시점에서 통행시간 데이터 분기가 나타났다고 판단하는 것이다.
Figure 5(b)와 Figure 5(c)는 통행시간 데이터 분기에 대한 xh(ti)의 임계값을 0.3으로 설정하였을 때의 각 MPR 조건에서의 TPR과 TNR의 결과이다. 본 단계의 분석에서 TP는 특정 MPR 조건에 해당하는 일부차량들의 통행시간 데이터를 기반으로 통행시간 데이터 분기가 나타났다고 판단했을 때, 실제로 데이터 분기가 나타난 경우를 의미한다. 다시 말해, 각 MPR 비율에 해당하는 일부 차량들의 통행시간 데이터만으로 계산한 xh(ti)와 전체 차량들의 통행시간 데이터를 통해 계산한 xh(ti) 모두 0.3보다 큰 경우를 의미한다. TN은 일부차량들과 전체차량들의 xh(ti)가 모두 0.3보다 작은 경우를 의미한다. MPR 조건별 분석에서 볼 수 있듯이, MPR이 매우 낮은 경우 TPR과 TNR 모두 낮은 성능을 보이지만, MPR 25% 이상에서는 MPR이 증가함에 따라서 두 지표가 모두 증가한다. 이러한 결과는 xh 지수를 활용하는 본 연구의 방법이 비교적 낮은 MPR 조건에서도 통행시간 데이터의 분기를 감지함에 있어서 합리적인 성능을 보인다고 할 수 있다.
2) 분기된 데이터 분류 분석
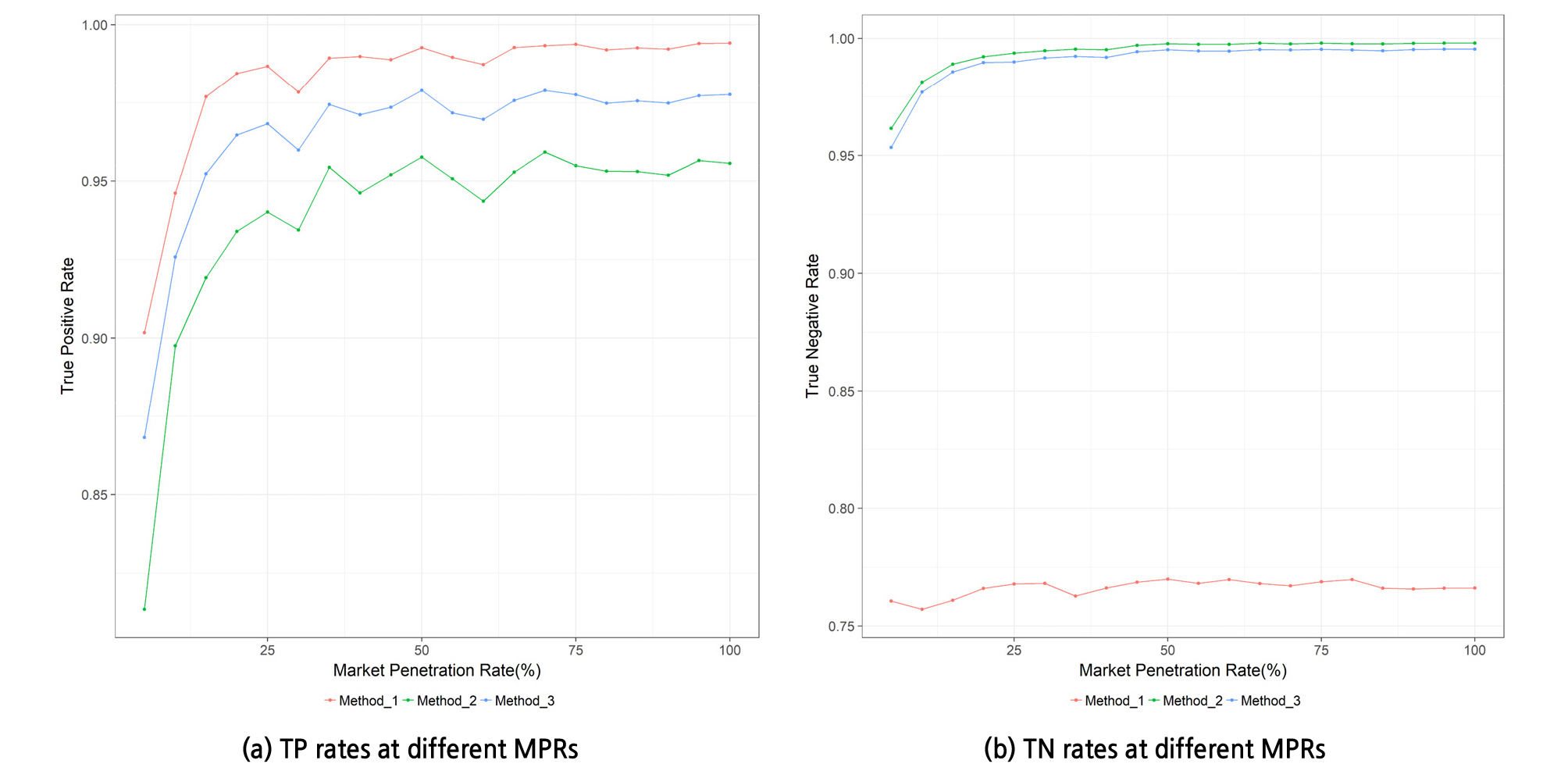
Figure 6은 분기된 데이터를 분류하는 3가지 방법의 결과를 보여준다. 본 단계의 분석에서 TP는 Gh1 그룹에 포함된 데이터 포인트가 실제 회전방향 교통류에 해당하는 경우를 의미하며, TN은 Gh2 그룹에 포함된 데이터 포인트가 실제 직진방향 교통류에 해당하는 경우를 의미한다.
Figure 6(a)에서 현시하는 바와 같이, MPR이 증가함에 따라 3가지 방법 모두의 TPR이 증가된다. MPR이 10% 이상일 때 모든 방법의 TPR이 0.9 이상으로 유사한 패턴을 보이면서 비교적 낮은 MPR 조건에서도 좋은 성능을 보여준다. TPR 측면에서는 ‘분류방법 1’이 가장 우수하며 ‘분류방법 2’의 성능이 가장 낮다. 반면에, Figure 6(b)의 TNR 측면에서는 ‘분류방법 1’이 전반적으로 현저하게 낮은 성능을 보이고, 다른 두 방법들은 낮은 MPR 조건에서도 0.95 이상의 높은 성능을 보인다. 이는 ‘분류방법 1’이 데이터 분포의 표준편차를 고려하지 않은 유일한 방법이기 때문이다. ‘분류방법 1’은 개별 데이터 포인트가 산술평균과 중앙값 중 어디에 더욱 가까운지를 단순하게 따지는 이분법적인 접근을 취하는 반면, 나머지 두 방법은 데이터 그룹의 산포도를 나타내는 표준편차를 근거로 데이터를 분류한다. 표준편차는 샘플링된 전체 데이터 포인트들을 모두 사용하여 계산되기 때문에, 표준편차의 활용은 통행시간의 변화폭과 같은 해당 데이터 그룹 전체에 대한 특성 정보가 반영되는 장점이 있어, ‘분류방법 2’와 ‘분류방법 3’의 성능이 ‘분류방법 1’에 비하여 높은 것을 볼 수 있다. 따라서 TPR 및 TNR 모두를 고려하였을 때 ‘분류방법 1’의 사용을 피해야 된다는 분석이 나온다. 해당 결과는 통계적 분포의 표준편차를 고려하는 것이 중요하다는 점을 보여주는 예시이다.
‘분류방법 1’을 제외한 다른 두 방법을 비교하면, TPR 측면에서는 ‘분류방법 3’이 ‘분류방법 2’ 보다 다소 높으며, TNR 측면에서는 ‘분류방법 3’이 ‘분류방법 2’ 보다 낮지만 그 차이가 미미하다. 따라서 TPR 및 TNR 모두를 고려하였을 때 ‘분류방법 3’이 가장 우수한 성능을 보이는 것으로 분석되며, 양 측면 모두 MPR 10% 이상에서 성능지수 0.95 이상을 보이므로 데이터 분류에 대한 우수한 성능을 보유한다. 다음 단계인 ‘데이터 이상치 제거’ 단계 대한 분석은 해당 방법을 적용한 데이터 분류 결과를 기반으로 진행한다.
3) 데이터 이상치 제거 분석
Figure 7에서부터 Figure 9까지는 데이터 이상치 제거 단계에 대한 분석 결과를 보여준다. 본 단계의 분석에서 TP는 Gh3 그룹에 포함된 데이터 포인트가 실제 데이터 이상치에 해당하는 경우를 의미하며, TN은 Gh4 그룹에 포함된 데이터 포인트가 실제 회전방향 교통류에 해당하는 경우를 의미한다.
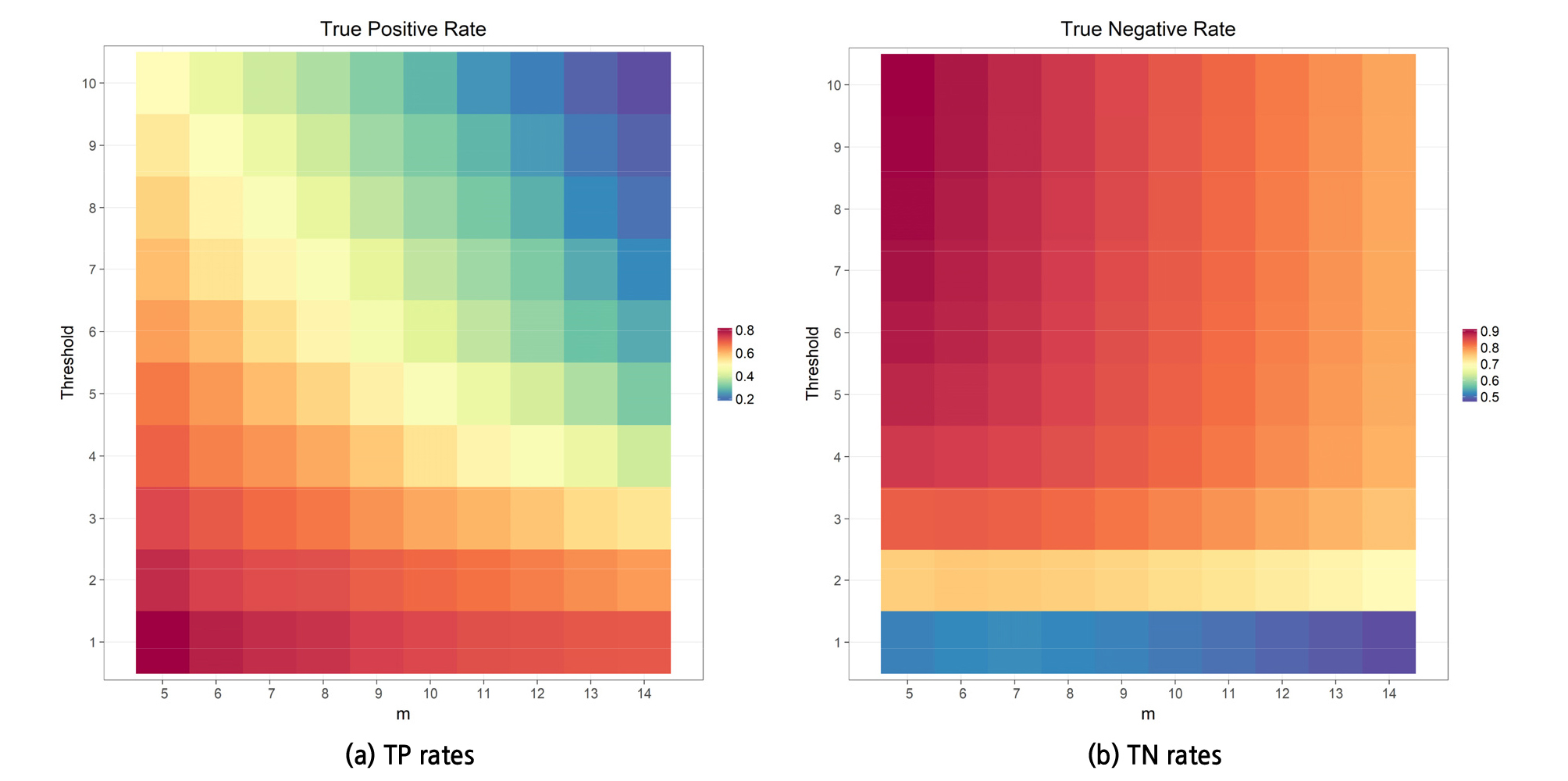
Figure 7(a)는 표준편차 범위의 상수계수인 yh와 이동평균의 샘플링 크기인 ah의 쌍에 각기 다른 값이 적용되었을 때의 TPR을 보여준다. 해당 등고선 그래프를 확인하면, 두 속성 모두가 가장 낮은 수준일 때(yh=1, ah=5) TPR 성능이 가장 우수하다. 반면, Figure 7(b)의 TNR 측면에서는 상수계수가 가장 크고 이동평균의 샘플링 크기가 가장 낮을 때(yh=10, ah=5) 가장 우수하다. 이러한 결과는 바탕으로 ah에 가장 적합한 값은 5임을 알 수 있다.
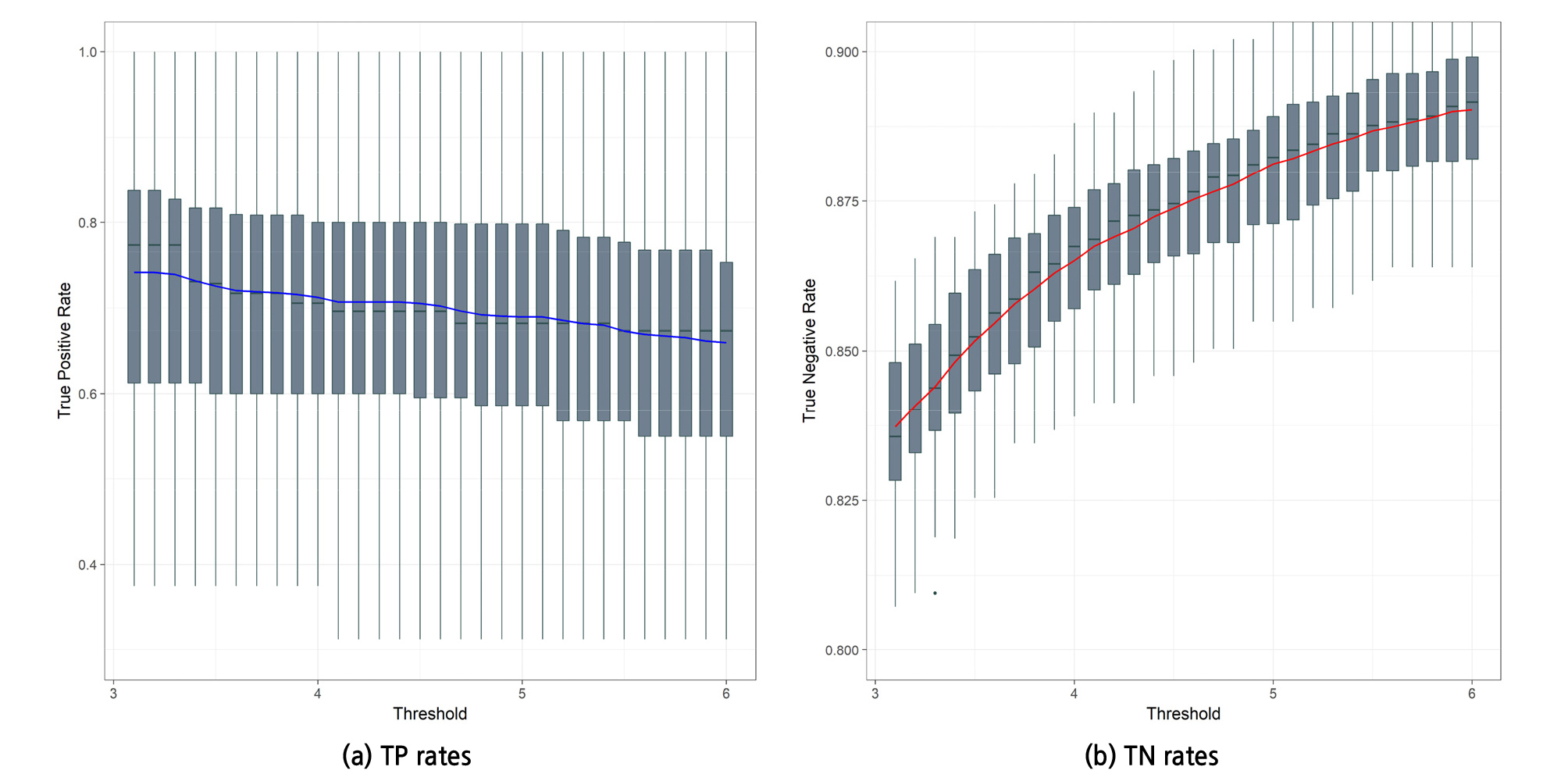
여기서의 문제는 상수계수인 yh에 적합한 값을 찾는 것이다. 따라서 Figure 8과 같이 추가적인 분석을 수행하였다. 해당 분석은 ah의 값이 5일 때의 yh의 값이 3에서 6 사이인 조건에 대한 TPR과 TNR 분석을 보여준다(그 이외의 yh 값들에 대한 분석은 TPR 및 TNR을 고려하였을 때 둘 중 하나의 성능지수가 0.6 미만이기 때문에, 부적합한 값들로 명백히 판단되어 제외). 해당 분석에서 TPR과 TNR 모두를 고려하였을 때, 가장 적합한 yh 값은 양쪽 모두 0.7 이상의 성능을 보인 4.5로 결과가 나왔다.
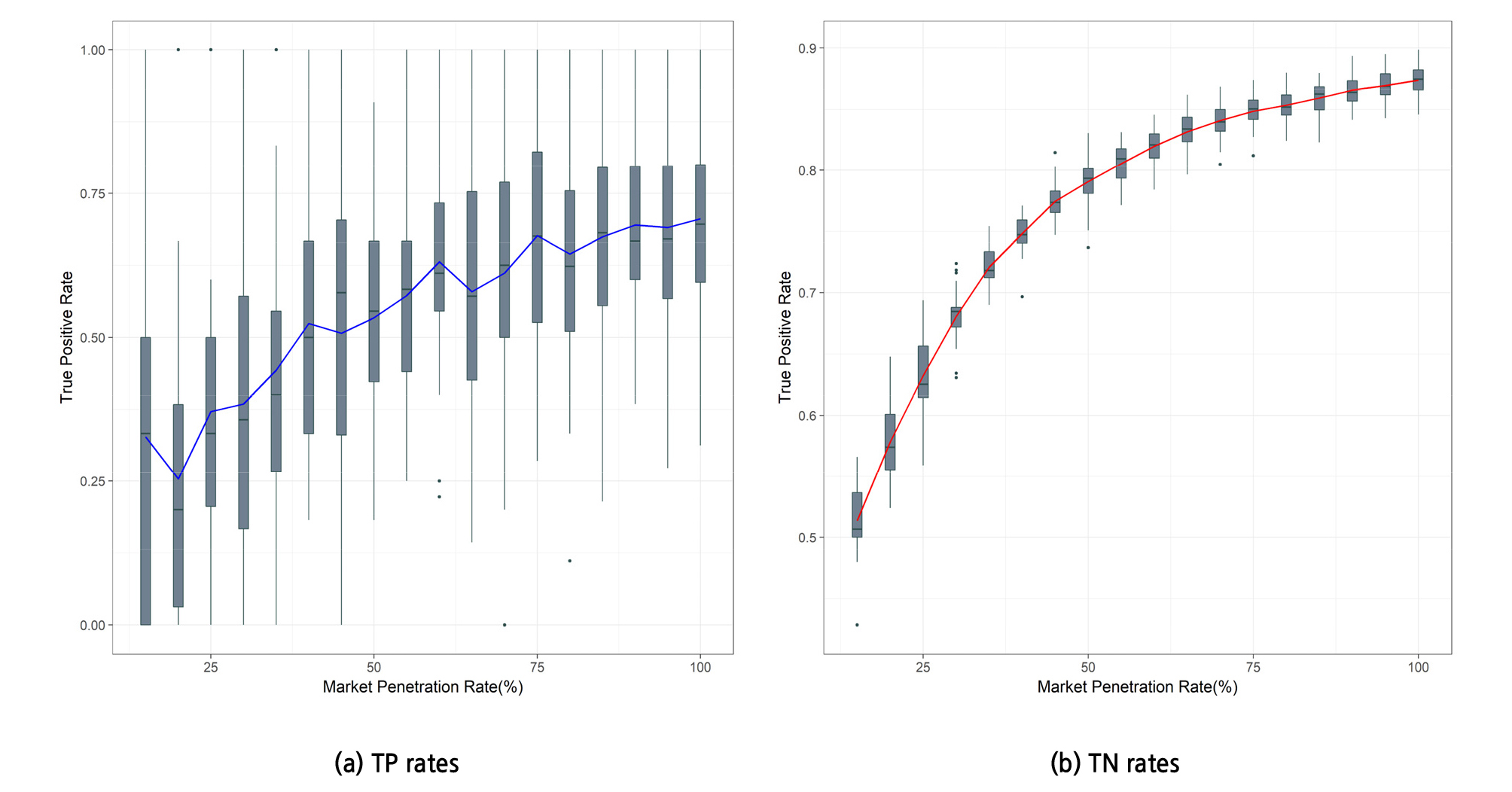
위와 같은 분석 결과에 따라서 해당 도로구간에 가장 적합한 yh=4.5 및 ah=5를 적용하였으며, 그 결과는 Figure 9와 같다. MPR 조건이 증가할수록 TPR 및 TNR 두 성능 모두 증가되는 경향을 보이지만, MPR이 60% 이상으로 비교적 높은 조건에서만 합리적인 성능을 보인다. 이는 Figure 2에서와 같이 실제 데이터의 이상치 중 일부가 회전방향 교통류에 해당되는 데이터의 추세에 포함되어 있어 이를 명확히 구분하기가 힘들기 때문에 나온 결과로 볼 수 있다. 또한 본 연구에서 활용한 시뮬레이션 데이터에서 실제 데이터 이상치의 양적인 수 자체가 적기 때문에 나타나는 현상이기도 하다. 따라서 추후 연구에서는 해당 방법이나 그 방법에 대한 실험 설정을 개선할 필요가 있다.
4) 진행방향별 통행시간 추정 성능 분석
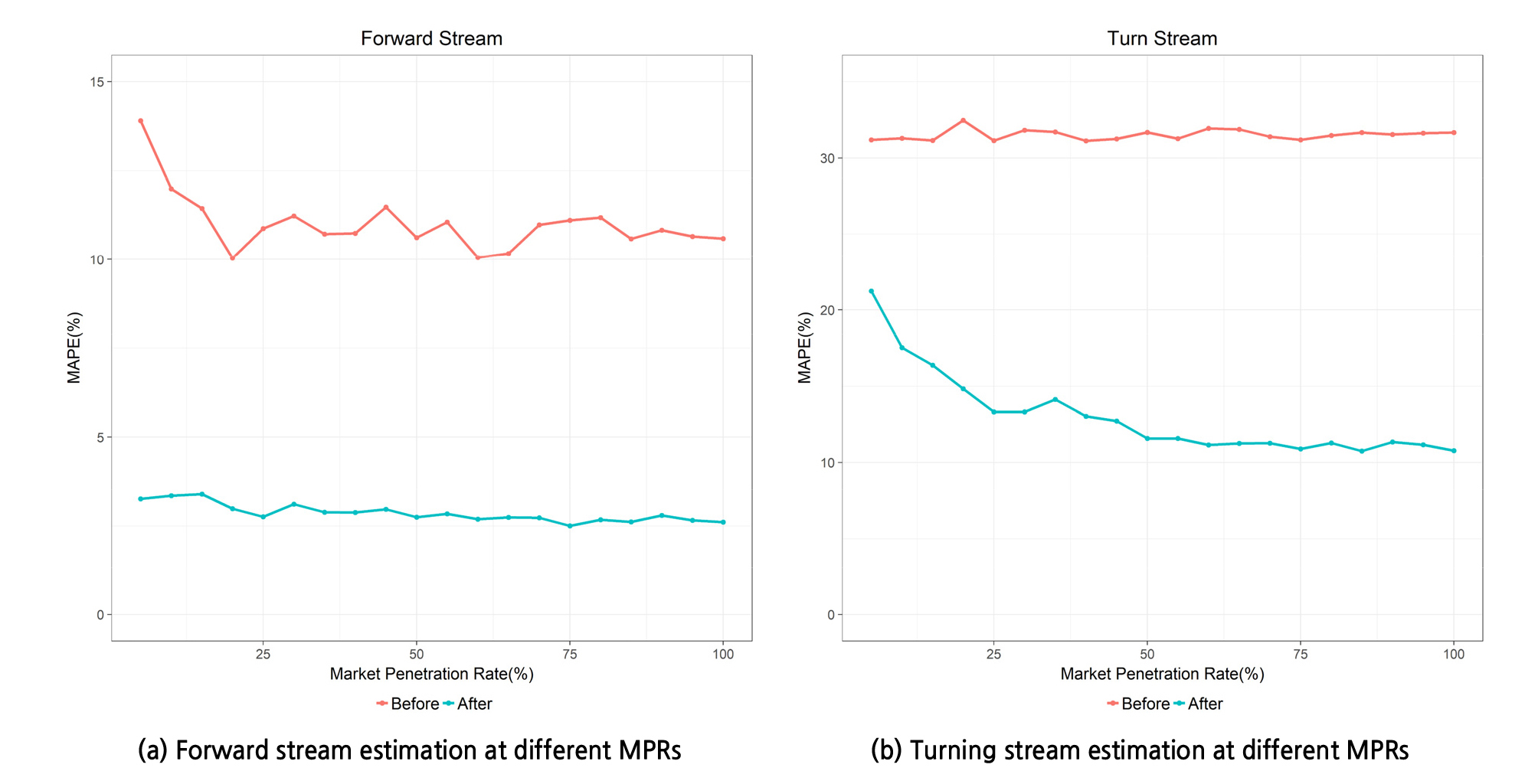
앞서 3개의 단계에 대한 분석의 결과를 기반으로 통행시간 추정 자체에 대한 성능 평가를 시행하였다. 분석 결과를 기반으로 찾은 개별 변수들의 적합한 값을 적용하였으며(xh=0.3, yh=4.5, ah=5), 데이터 분류에는 ‘분류방법 3’을 적용하였다. 본 연구에서 제시한 방법을 적용하기 전후에 대한 비교를 평균절대비율오차(Mean Absolute Percentage Error, MAPE)를 산출하여 수행하였다. 전자에 의한 통행시간 추정은 모든 Thn(ti)의 산술평균 산출하여 해당 값이 직진방향 및 회전방향 교통류에 동일한 통행시간으로 추정하였다. 후자인 본 연구의 방법에 의한 추정은 Gh2(ti) 그룹에 포함된 데이터 포인트들의 산술평균을 직진방향 통행시간, Gh4(ti) 그룹에 포함된 데이터 포인트들의 산술평균을 회전방향 통행시간으로 추정하였다.
Figure 10은 다양한 MPR 조건에서의 직진방향과 회전방향 통행시간 추정 성능을 분석한 내용이다. 해당 그래프는 본 연구의 방법을 적용하기 전과 후의 MAPE 기반 추정 오차율의 비교를 보여준다. 본 연구의 방법을 적용하였을 때 직진방향과 회전방향 통행시간 추정 모든 측면에서 추정 오차율이 감소된 것을 볼 수 있다. 특히, Figure 10(b)의 회전방향에서는 MPR이 20% 이상일 때 MAPE 15% 미만의 합리적인 성능이 나타나며, 이는 앞서 분석된 바와 같이 회전방향 데이터 중 이상치를 제거함에 있어 비교적 높은 MPR 조건에서만 적정 성능을 보이기 때문에 나타난 결과이다. 따라서 본 연구에서 제시된 통행시간 별도 추정 방법은 MPR이 20% 이상일 때 활용 적정성이 확보될 것으로 판단된다. 이에 더불어 향후 이상치 제거 방법에 대한 개선이 수행된다면 본 연구의 방법은 전반적인 MPR 조건에서 합리적인 성능을 보여줄 수 있을 것으로 전망된다.
또한, 매 5분간 수집된 타임스탬프 데이터를 기반으로 수행되는 ‘통행시간 데이터 분류’ 기능의 전체 프로세스(데이터 분기 감지-분기된 데이터 분류-데이터 이상치 제거)는 1개 도로 구간에 대하여 평균 계산시간(computation time)은 Intel(R) Core(TM) i5-8500 CPU 및 RAM 16GB의 데스크톱 사양 기준으로 0.83초 이내이다. 이는 본 연구에서 제시하는 방법의 실시간 적용 가능성을 보여주며, 매 5분마다 실시간으로 교통정보를 표출하는 현행 ATIS의 운영 요구조건에도 부합한다.
결론
본 연구에서는 타임스탬프 데이터를 기반으로 고속도로 분기지점 상류부에서 진행방향 교통류별 통행시간을 별도로 추정하는 방법을 제시하였다. 해당 방법은 단일 도로 구간에 대한 차량들의 진입 및 진출 시간들의 기록을 입력 데이터로 활용하며, 주어진 시간 간격마다(예: 매 5분) 수집된 입력 데이터를 기반으로 개별 차량들의 진출 및 진입 시간의 차이를 계산하여 해당 도로의 통행시간 값들에 대한 샘플링을 수행한다. 그런 다음 샘플링이 완료된 데이터 포인트들에 통계 분석을 적용하여 직진방향 교통류(forward stream) 및 회전방향 교통류(turning stream)에 해당하는 데이터 포인트들로 분류하고, 분류가 완료된 데이터 포인트들을 기반으로 해당 도로구간 내 각 진행방향별 교통류에 대한 통행시간을 별도로 추정한다.
본 연구에서는 특히 통행시간 데이터 분류 기능 구현 측면에서 세부 방법 개발을 위한 다양한 분석을 수행함에 중점을 두었다. 해당 기능을 ‘데이터 분기 감지’, ‘분기된 데이터 분류’, ‘데이터 이상치 제거’의 순차적인 3개의 단계로 구성하였다. ‘데이터 분기 감지’에서는 진행 방향별 통행시간의 차이 발생 여부를 감지할 수 있는 통계적 분석 기반의 새로운 지수를 제시하였으며, 이는 데이터 포인트들의 분기 여부를 판단할 수 있는 임계값을 찾는 데에 유용한 것으로 평가되었다. ‘분기된 데이터 분류’에서는 통행시간 차이가 감지되었을 때 이를 각 방향별로 데이터를 분류할 수 있는 3가지의 통계적 접근 방법을 실험하였으며, 현재 한국도로공사에서 데이터 이상치 제거에 사용하고 있는 방법을 개정하여 제시한 본 연구의 방법이 데이터 분류에 우수한 성능 보유하고 있음을 보여주었다. ‘데이터 이상치 제거’에서는 차량의 주행 중 정차와 같은 비정상적인 행태를 보이는 데이터를 제거하기 위하여 단순이동평균 기반의 분석 방법을 적용하였으며, 이는 probe 차량의 MPR이 높은 경우에만 합리적인 성능을 보여주었다. 또한, 앞서 3개의 단계에 대한 분석의 결과를 기반으로 통행시간 추정 자체에 대한 성능 평가를 시행하였다. 이 평가를 통하여 본 연구의 방법을 적용하였을 때 직진방향과 회전방향 통행시간 추정 모든 측면에서 오차율이 감소된 것을 보여주었다.
본 연구에서 제시하는 방법은 타임스태프 데이터와 같은 단순화된 데이터를 활용하여 실시간적 실용성을 추구함과 동시에, 통행시간 별도 추정의 정확도를 향상시키기 위하여 위 3단계 분석의 체계적인 구성을 새롭게 제시한다는 점에서 연구적 가치가 있다. 기존의 ATIS에서는 도로구간에서 수집된 통행시간 데이터 포인트들을 통상적으로 평균값을 산출하는데, 이는 분기지점에서의 차량 진행방향별 상세정보를 표출하는 데에 한계점이 있으며, 이를 개선하기 위한 차량 내비게이션 서비스 업체들의 기술 개발 요구가 증가되고 있다. 또한, 향후 자율주행차량 운영 측면에서도 도로의 차로별 교통상태 정보를 필요로 하는 고정밀 지도(HD Map) 구현을 위한 다양한 데이터 수집 및 분석 솔루션 개발에 대한 요구가 증가하고 있다. 본 연구에서 제시한 방법은 내비게이션 경로제공 서비스 향상 및 자율주행차량 운영을 위한 HD Map 서비스 구현에 일조할 수 있는 방법으로서, 향후 ATIS 및 ATMS 고도화에 활용될 수 있을 것으로 기대된다.
본 연구에서 제시한 방법은 다양한 분석을 통하여 합리적인 성능을 보여주었으나, 여러 한계점도 있다. 본 연구에서는 분기된 데이터에 대한 몇 가지 단순 통계기법만을 분석하였으며, 보다 우수한 성능을 보일 수 있는 다른 기법을 찾는 작업을 추후 연구에서 수행하여야 할 것이다. 또한 본 연구에서 수행한 데이터 이상치 제거 단계에 대한 분석은 probe 차량의 MPR이 높은 경우에만 합리적인 성능을 보였기 때문에 이를 개선할 수 있는 추가적인 연구가 필요하다. 마지막으로 본 연구의 범위는 고속도로 분기지점에 중점을 맞추었으며, 추후 연구에서 해당 연구의 범위를 도시부 도로 교차로와 같은 단속류 지점으로 확장할 필요가 있다.