서론
인공지능(AI) 알파고의 등장과 함께 가상현실, 사물인터넷(IoT), 로봇, 생명공학, 증강현실(AR) 등 4차 산업혁명의 다양한 기술들이 도입되고 있다. 교통 분야에서 4차 산업혁명의 다양한 기술로 가장 크게 영향을 미치는 것은 자율주행차량(Autonomous Vehicle, AV)이다.
자율주행차량(AV)은 사람의 조작 없이 자동차가 스스로 움직일 수 있는 것으로 차량 내 장착되어있는 첨단센서가 사람처럼 사물 간 거리를 측정하여 위험을 감지하고 주변상황 및 도로상황을 파악하여 안전하게 주행할 수 있도록 한다. 또한, 현재 위치와 주변상황 정보를 실시간으로 수집하여 각 상황에 맞게 최적경로로 통행할 수 있는 전략적인 서비스를 제공하도록 한다.
자율주행차량(AV)은 V2X (Vehicle to Everythings) 통신기술에 의해 외부의 주변 환경 인식 및 경로탐색을 수행하며, 통신하는 매개체에 따라 V2V (Vehicle to Vehicle)와 V2I (Vehicle to Infra)로 구분된다. V2V 통신기술은 차량 간 통신으로 실시간 교통상황이나 돌발상황, 교통류 제어상태 등에 활용되며, V2I 통신기술은 차량과 인프라 간 통신으로 전방 교통정보, 차량 접근 알림, 추돌경고 등의 정보를 교환한다. 즉, 도로와 자율주행차량(AV)이 상호간의 커뮤니케이션을 하면서 차량의 운행과정을 조절하는 것이다.
현재 논의되고 있는 자율주행차량(AV)은 개별 차량 차원에서 최종 목적지까지 주변상황을 고려하여 자동적으로 운행하는 것으로 자율주행차량(AV) 주행 특성상 도로 인프라 환경과 신호제어 등 관련 시설 구축 및 관리, 자율주행차량(AV)의 운영을 위한 준비과정이 필수적이다. 자율주행차량(AV) 도입 및 상용화를 위해 자율주행차량(AV) 관련 파라미터 설정, 기능 및 인식 개선, 차량 제어 알고리즘 등의 다양한 연구가 진행 중에 있다. 특히, 자율주행차량(AV)의 운행에 있어서 Navigation-Guidance-Control 중 차량은 Guidance와 Control에 해당되나 교통운영자 입장에서는 자율주행차량(AV)의 V2X (Vehicle to Everythings) 통신기술에 의해 수집되는 구간별 운행시간 정보를 활용하여 정해진 경로가 아닌 모든 도로망 내 효율적으로 자율주행차량(AV)을 분배하는 방안이 필요하다. 하지만, 현재는 자율주행차량(AV)을 위한 도로 교통 인프라를 구축하는 데에만 치중하고 있는 실정이다.
이를 위해 본 연구에서는 자율주행차량(AV)의 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS)을 도입하고자 하며, 최적경로 탐색 시스템(DRGS) 구축을 위한 개념 정립 및 연구의 방법론을 제시하고 경로탐색 방법론에 대한 이론적 고찰 및 Simulation 환경 내 구현하는 방안을 Case Study에 적용하여 개발한 방법론의 정당성을 확보하는데 목적이 있다.
최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS)은 주어진 Network 내 출발지/도착지(O/D) 간 주행차량이 일정시간 간격으로 교통상황을 판단하여 최적경로로 안내하는 시스템으로 경로 탐색 관련 파라미터를 통해 목적지까지 새로운 경로를 탐색하며 통행하는 것이다.
현재 대상지 특성이 있는 도로망에 출발지/도착지(O/D, Origin/Destination)에 따라 통행배정(Assignment)하는 기법은 다양하게 있으며, 이 중 Equilibrium 기법은 “통행자가 도로 전체에 대해 통행시간을 알고 있다는 전제하에 최적경로를 운행” 한다는 알고리즘에 기반하고 있다. 자율주행차량(AV)은 V2X에 의해 자신의 통행시간 정보를 교통정보센터에 전송하고 교통정보센터는 도로 전체 구간에 대해 실시간 통행시간 정보를 공유함으로써 개별 차량에 대한 최적경로 제공이 가능하다는 것을 알 수 있다.
따라서 자율주행차량(AV) 도입 시, 기존 Network 내 최적경로 통행과 교통상황에 따른 효율적인 교통운영관리를 위해 다양한 통행배정(Assignment) 기법 중 통행시간 정보를 활용한 Equilibrium Assignment 기반의 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS) 도입을 목적으로 한다.
이론적 고찰
최적경로 탐색 시스템(DRGS)에서 가장 중요한 것은 경로탐색이다. 어떤 방법론을 통해 최적경로를 탐색하는지, 다양한 경로 중 어떤 기준에 의해 운전자를 위한 적정 경로를 지정하는지, 다양한 교통상황이 존재할 때 최적경로를 탐색하는 방법이 무엇인지에 대해 관련 연구들을 검토하였다.
최적경로를 탐색하는 방법으로는 교통데이터를 통해 교통상황을 분석하여 다음 교통상황을 예측하고 이를 통해 최적경로를 탐색한다. 여기서 주어진 출발지/도착지(O/D)에 대해 통행비율을 산정하고 프로그램을 통해 출발지의 과거이력데이터와 현재의 출발지/도착지(O/D)의 통행속도를 비교함으로써 두 경로에 대한 통행시간이 사전 설정한 값을 초과하였을 때 새로운 경로가 생성되며, 이러한 경로를 업데이트하고 이를 기반으로 새로운 최적경로가 생성되는 것이다(Lam et al., 1992). 과거와 현재의 교통데이터를 통해 최적경로를 탐색하는 방법과 달리 교통데이터뿐만 아니라 교통체증이 발생하는 교통상황을 예측하여 최적경로를 탐색해야한다는 연구도 있다. 차량 주행 시, 교통신호에 의해 대기행렬 및 지체시간이 발생되는데 여기서 교통신호는 확률적 특성을 갖기 때문에 장래의 교통상황을 예측할 수 없어서 차량이 경로를 변경하였을 때, 동일한 목적지와 동일한 교차로에 도착하는 모든 차량은 동일한 경로로 안내되어 해당 경로를 통행할 때 교통체증이 발생할 수 있다는 것이다. 즉, 통행하는 차량대수를 고려하여 경로를 재탐색하는 것으로 경로를 변경한 차량이 차지하는 공간은 해당 도로 구간에 통행하는 차량에게 불이익을 제공할 수 있으므로 이를 고려하여 다음 차량에게는 경로를 재탐색하여 원활한 통행이 될 수 있도록 하는 것이다(Kim et al., 2016). 이와 유사하게 혼잡 위험이 있는 링크에게 불이익을 주고 신뢰할 수 있는 경로를 제안할 수 있도록 A* 알고리즘과 Chen의 Link penalty 방법 기반의 경로 탐색 방법론 연구가 있으며(Kaparias et al., 2007), 이 외에도 차량의 속도를 고려하여 차량의 위치를 통해 적정 경로를 탐색하기도 한다(Treiber and Kesting, 2013).
주어진 교통상황에서 교통데이터를 기반으로 다양한 방법을 통해 출발지/도착지(O/D) 간 최적경로를 탐색하고 이를 통해 제공되는 최적경로를 선택하는 것은 다양한 기준에 의해 정립될 수 있다. 교통데이터를 기반으로 최적경로를 탐색하나 실제 운전자의 취향에 따라서 운전자 입장에서의 최적경로는 변경될 수 있다. 즉, 차량에 구축되어있는 Navigation 시스템의 경로를 선택하는 부분에서 운전자의 행동을 모델링하여 최적경로를 제공하는 것으로 Fuzzy-Neural (FN) 접근법을 활용하였다(Pang et al., 1999). FN 접근법에서는 운전자 경로 선택 속성값의 상관관계를 분석하였으며, 운전자의 경로 선택에 대해 훈련이 진행되어 운전자에게 추천 경로 또는 경로에 대한 순위를 제공한다. 이 연구에서는 운전자의 선호도에 따라 경로 선택 방법의 방향을 지정할 필요가 있음을 강조하였다. 이 연구와 관련하여 해당 네트워크에서 경로 선택을 위해 네트워크 내 통행량을 산정하는 모델을 고려하여 경로를 선택하는 것에 대한 연구가 진행되었고(Bovy and Stein, 1990) 도로 이용자에게 최적경로를 제공하기 위해서 먼저 교통량 데이터를 실제 통행시간과 교통량을 산정하기 위해 활용되며, 도로 이용자에게 개별 선호도를 고려하여 최적경로를 제공하는 것으로 총 2단계에 걸쳐 경로를 안내하는 연구가 진행되었다.
ATIS의 도입으로 개인 차량의 주행 효율을 높이기 위해 실제 교통상황을 고려해야하며, 주행 차량은 가속도, 제동 등 차량 운행 시, 시간 간격(gap)을 고려하여 최적의 운전전략이 필요하다는 것이다. 1단계는 온라인 기반 Simulation에 의해 통행시간, 밀도 등 실제 교통상황에 대한 정확한 정보를 고려하고 다양한 통행 경로를 계산하여 최적경로를 산정하는 것이다. 일반적으로 운전자는 주관성이 높기 때문에 최적경로를 결정하기 어려우므로 2단계에서는 통행시간, 밀도, 도로 유형, 경로의 길이 총 4가지 기준에 의해 운전자 선호가 다른 것으로 정의하였으며, 4가지 기준은 S형 함수로 설명되고 가중치가 크고 중요도가 낮은 기준(통행시간 감소를 위해 통행거리가 증가되어서는 안됨)을 반영하였다(Wahle et al., 2001).
운전자의 선호도에 대한 기준에 대해 경로 변경에 대한 순위와 통행시간을 고려하여 우회경로를 산정하는 방법을 제시한 연구도 있다. 차량 수준에 맞춤형 경로안내를 생성하도록 미세한 경로 재탐색 전략에 대해 논의한 것으로 먼저 주기적으로 실시간 교통량 데이터를 기반으로 사전에 교통혼잡 임계값과 용량을 정의하며, 이를 통해 교통량 분석 및 예측을 수행하고 주행 시, 통행시간 단축에 더 많이 기여할 수 있는 차량에게 경로 재탐색 우선순위를 높게 하여 제공하는 것이다. 우선순위 기준으로는 현재 위치에서 목적지까지의 통행거리, 목적지에 가까울수록 차량 경로를 다시 탐색해야 할 필요성과 차량의 우회경로 경우의 수, 우회경로를 통해 절약할 수 있는 통행시간, 기존 경로와 우회경로 차이로 구성되어 있다. 이러한 기준을 통해 효율적인 통행시간을 산정하여 우회경로를 탐색하고 이를 각 차량에 개인별 경로를 제공하며, 차량은 기존 경로로 유지할지 변경된 경로를 전환할지를 선정한다(Liang et al., 2014).
다양한 교통상황이 존재하는 교통환경에서 통행시간의 확률적 특성으로 인해 정확한 교통상황을 인지하는 것은 굉장히 어려운 부분이므로 실시간 교통데이터의 활용과 해당 교통상황에 적합한 경로탐색이 필요하다. 최적성에 대한 기준과 제공되는 최적경로는 각 링크에서 통행시간의 무작위 특성을 설명해야 한다. 일반적으로 해결하기 어려운 통행시간 가변성에 대한 문제에 대해 효율적인 알고리즘을 제시한 연구가 진행되고 있다(Fu and Rilett, 1998). 링크의 가중치가 독립적이고 변하지 않을 경우 각 링크별 시간 종속 가중치를 사용하는 동적 프로그래밍을 사용하여 문제를 해결할 수 있다고 제시하였으며(Astarita, 1996; Dean et al., 2004), 최적경로를 탐색하기 위해 무한한 반복횟수를 필요로 하는 기존 경로탐색 알고리즘을 개선하여 통행시간을 기반으로 최적경로를 결정하는 적응형 알고리즘(Adaptive optimal strategy and methods)을 제시하였다(Samaranayake et al., 2012). 기존 SOTA (Stochastic online Arrival)를 보완하고자 시시각각 변하는 교통상황과 링크 통행시간 분포의 시공간 관계를 분석하여 새로운 알고리즘을 제시하였다. 또한, Fast Fourier Transform (FFT)와 새로운 알고리즘을 통해 효율적으로 경로 탐색에 대한 속도 향상 기술을 제시하였다. 다양한 경로탐색에 의해 최적경로 제공 시, 선택한 경로가 예측과 일치할 수 있어야 한다.
분산형 경로안내(Decentralized route guidance) 시, 예상 혼잡에 대한 예측 기술을 제안하여 시간에 따른 링크별 통행시간을 산정하고 운전자와 통신할 때, 이 예측과 일치하는 시간에 따라 가장 빠른 경로로 유도하는 것이다. 이 연구는 SAVaNT (Simulation of Anticipatory Vehicle Network Traffic) Simulation의 반복과정을 통해 통행시간을 예측하였다(Kaufman et al., 1991; Wunderlich et al., 2000). 즉, SAVaNT 방법을 통해 링크의 통행시간을 예측하며, 예측된 링크 통행시간의 정확성을 높이기 위해 Backdating 기술을 활용하였다. 이를 통해 최적값을 얻을 수 있도록 하며, 최적값을 얻을 때까지 Simulation을 수행하였다. 다양한 경로탐색 기법으로 일반적으로 도시교통 혼잡을 줄이고 교통흐름 및 교통안전을 개선하는 데 최적경로 탐색 시스템(DRGS)은 중요한 역할을 할 것으로 예상된다.
하지만 자연재해, 교통사고 등 특정 교통상황(유고상황)이 발생하였을 때의 경로 안내는 더욱더 중요한 부분이다. 이러한 비반복 상황에 대한 정확한 예측을 제공할 수 있는 예측 알고리즘은 교통관리 시스템의 의사결정 기능을 향상시키며, 예측을 위한 적정 간격(예를 들어 30초 간격 데이터)이 중요하다고 제시하였다(Vlahogianni et al., 2014). 이 연구에서는 Wardrop에 의해 제시된 Equilibrium Assignment 원칙을 기반으로 최적경로 탐색 시스템(DRGS)에서 경로탐색 시, 최소경로를 선택할 때 평균 통행시간을 고려하는 User Equilibrium (UE)과 각 링크에서 한계 통행시간을 고려하는 System Optimal (SO)에 대해 논의하였고 고속도로, 간선도로 등 교통상황별 교통사고 발생 여부에 따라 UE와 SO 방법을 비교 분석하였다. 또한, 정상적인 교통상황에서는 소수의 운전자만 균형상태를 유지하기 위해 경로를 재탐색하지만 비반복적인 교통혼잡으로 인한 특정 교통상황에서는 대부분의 운전자가 불균형상태를 벗어나고자 최적경로 탐색 시스템(DRGS)이 필요하다고 주장하였다. 교통상황에 적합한 경로안내를 위해 교통사고에 의한 대기행렬 및 지체시간을 추정하였으며, 도로 유형 및 교통상황별 경로탐색 전략을 적용하여 분석하였다. 최적경로 탐색 시스템(DRGS)에서 경로탐색 전략을 SO 방법은 전체 통행시간을 감소시킬 수 있다는 장점이 있고 특정 교통상황에서도 효율적으로 적용될 것으로 예상하지만 예상과는 달리 이미 네트워크에 대해 잘 알고 있는 운전자는 경험을 바탕으로 자신이 알고 있는 경로를 통행하는 경우가 많으며, 여기서 한계수준을 초과한다고 생각될 때만 경로를 변경한다는 것에서 문제가 되었다. UE와 SO 방법으로 통행시간은 교통조건과 네트워크 구성에 따라 달라지므로 통행시간 변화를 고려하는 Adaptive routing 전략이 필요하다고 제시하였다. 즉, 다양한 교통상황에 있어 2가지 방법을 단독으로 사용하는 것보다는 UE 및 SO 방법을 통해 최소통행시간 절감 비율을 산정하며, 통행시간 비교를 통해 최적 방법을 현재 교통상황에 적용하는 Adaptive routing 전략이 더 효율적이라는 결론을 제시하였다(Lee, 1996).
살펴본바와 같이 최적경로 탐색 시스템(DRGS)을 위한 경로탐색 관련 연구는 교통량 및 통행시간 데이터를 활용하여 새로운 경로를 탐색하고 교통상황을 고려하여 차량별 경로를 재탐색해야한다고 제시하였다. 또한, 운전자 선호도에 따른 최적경로 선정 기준을 제시하며, 교통상황에 적합한 경로를 안내받을 수 있도록 다양한 Simulation 및 통행배정 기법을 활용하였다.
본 연구에서는 각 링크 별 통행시간을 분석하여 차량에게 최소의 통행시간을 제공할 수 있도록 개별 차량마다 일정시간 간격으로 경로를 탐색하고 경로 선택에 있어 운전자의 선호도를 고려하고자 하나 본 연구의 목적은 일반차량이 아닌 운전자가 없는 자율주행차량을 기준으로 출발지/도착지(O/D)간 최적경로 안내를 제공받는 것을 전제로 하기 때문에 관련 통행시간, 통행거리 등의 운전자 행동 모델링과 관련 있는 파라미터를 조정하여 본 연구를 진행하였다. 또한, 다양한 교통상황에 적합한 경로를 제공하기 위해 Wardrop 원칙의 Equilibrium Assignment를 기반으로 경로탐색을 진행하고자 하며, Simulation 네트워크 환경을 활용하여 SOTA에 적용된 Stochastic Assignment와 비교로 최소 통행시간에 따른 적절한 통행배정(Assignment) 기법을 선정하고자 한다.
연구의 방법론
자율주행차량(AV) 도입에 따른 최적경로 안내를 위해서는 자율주행차량(AV)의 운영을 위한 다양한 파라미터를 고려해야한다. 이 중 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS) 구축을 위해 해당 Network의 출발지/도착지(O/D) 간 전체적인 통행시간(Travel Time) 정보가 필요하다. Figure 1과 같이 Network 내 시간대별 최적경로 탐색을 위해 Dynamic Assignment 기법을 활용하며, 다양한 경로탐색 시, 통행시간 정보를 파악할 수 있고 최적경로를 탐색하는 Equilibrium Assignment를 적용하여 수행하고자 한다(동적 사용자 평행배정 기법, Dynamic User Equilibrium Assignment). 또한, 자율주행차량(AV) 주행 시, 최적경로를 탐색하는 탐색시간 간격(Interval) 파라미터 조정에 따른 Route Guidance를 설정함으로써 자율주행차량(AV)의 적정 경로탐색 시간을 추정하며, 이러한 과정을 통해 최적의 교통정보 제공에 따른 경로를 안내하여 도착지까지 안전하고 빠른 통행을 하도록 한다. 자율주행차량(AV)의 파라미터 중 탐색시간 간격(Interval) 외에도 다양한 적정 파라미터를 선정하여 향후 효율적인 자율주행차량(AV)의 운영을 기대하고자 한다.
본론
본 연구에서는 자율주행차량(AV)의 차량특성 및 교통정보를 활용하여 Network 차원의 차량 통행시간이 최소화되는 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS)을 도입하고자 하며, 시스템의 통행배정(Assignment) 및 경로탐색(Route Guidance) 알고리즘에 대해 제시하고 교통 전문분석 Software인 Microscopic Simulation model VISSIM을 활용하여 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS) 도입에 따른 효과분석을 시행하고자 한다.
1. Dynamic Route Guidance system 구축원리
1) 시스템 구축원리
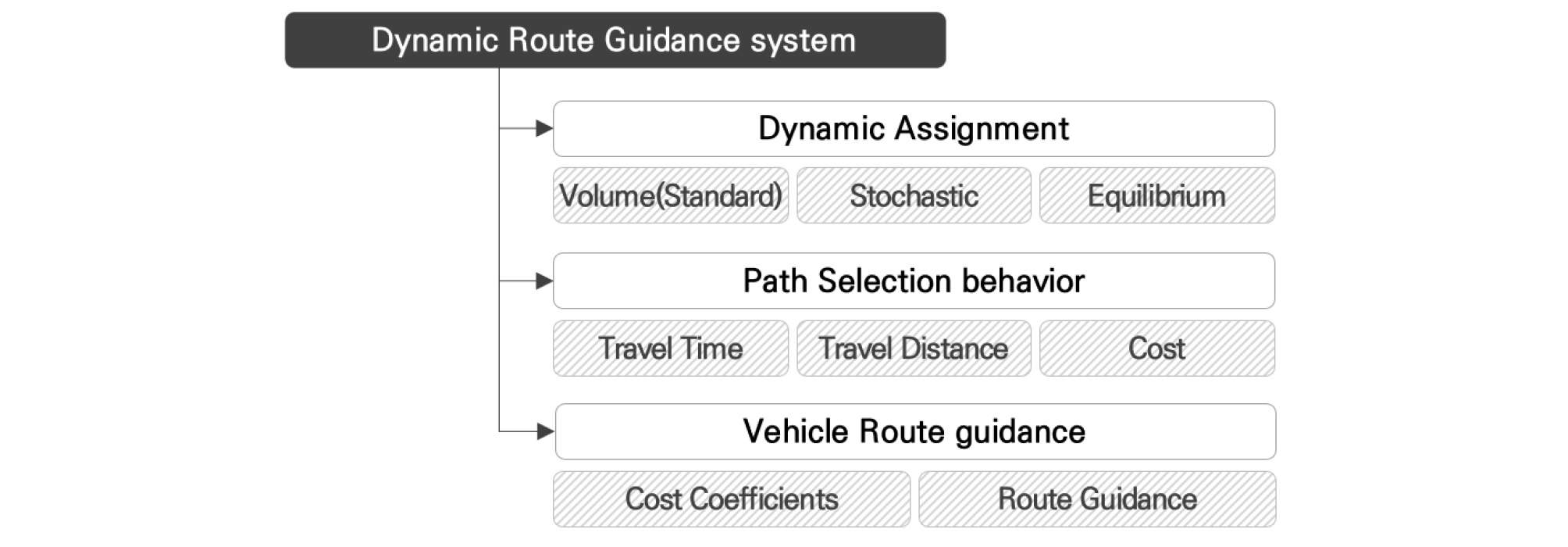
최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS)은 통행배정(Assignment) 기법과 다양한 파라미터를 활용하여 최적경로를 탐색하는 것으로 출발지/도착지(O/D) 간 주행 차량이 일정 간격으로 교통상황을 판단하여 최적경로로 안내하는 시스템으로 시스템 구성은 Figure 2와 같다.
시스템 내 구축원리로는 동적 사용자 평행배정 기법(Dynamic User Equilibrium Assignment)을 기반으로 통행시간(Travel Time), 통행거리(Travel Distance), 비용(Cost) 등의 파라미터를 통해 경로(Path)를 결정하며, 경로탐색(Route Guidance)을 통해 일정시간 간격(Interval) 및 파라미터를 활용하여 최적경로를 탐색한다.
2) 통행배정(Assignment) 알고리즘
출발지/도착지(O/D) 간 통행배정(Assignment) 기법은 다양하게 존재하며, 이 중 Route Guidance를 위한 동적 통행배정 기법(Dynamic Assignment)은 시간대별 O/D Matrix를 통해 차량이 통행하는 기법으로 Simulation 기반 경로탐색 기법으로는 Volume (Standard) 기법, Stochastic 기법, Equilibrium 기법으로 구분된다.
Volume (Standard) 기법은 기존 경로의 교통량을 가지고 경로를 탐색하는 기법으로 설정한 시간대에 해당하는 O/D Matrix를 기반으로 통행하는 기법이다. 모든 출발지/도착지(O/D)의 교통량은 변하지 않으며, 수요분석결과로부터 얻는 데이터를 활용한다.
Stochastic 기법은 사전 반복으로 평활화된 일반화비용을 고려하여 모든 경로를 탐색하는 것으로 비용이 많을수록 차량이 적게 분포하고 비용이 적을수록 차량이 많이 분포하며, 비용이 같으면 교통량과 관계없이 통행배정(Assignment)되는 기법이다. 실제 통행시간이 아닌 이용자의 인지시간에 근거하여 통행을 배정하고 인지시간은 실제 통행시간을 평균으로 한 일정한 확률분포를 가지는 것으로 가정한다. Logit 모형과 같은 배분모형에 기초하여 다양한 경로에 배정되어 많은 경로를 탐색한다.
Equilibrium 기법은 Wardrop의 ‘도로를 이용하는 운전자들 간에는 균형이 존재하며, 균형 상태에서는 자신의 경로를 임의로 변경해서 이익을 얻을 수 없는 상태로 정의 된다’ 는 이론에 기초한다. 가능한 많은 경로 중 최적경로를 탐색하는 기법으로 비용에 비례한 경로를 통해 각각의 O/D마다 교통수요를 재분배하여 평균치보다 높은 비용이 발생하면 교통량은 감소하고 평균치보다 낮으면 기존보다 교통량이 증가하는 것이다.
본 연구에서는 제시된 동적 통행배정 기법(Dynamic Assignment) 중 대상지 특성을 고려하고 통행시간 최소화가 가능한 Equilibrium 기법을 활용하고자 한다. Equilibrium 기법의 알고리즘에서 먼저 통행시간(Travel Time)을 결정하기 위한 식은 Equation 1과 같다. 통행시간(Travel Time)은 Simulation 내 모든 통행 구간과 분석 간격에 의해 산정되며, 통행 구간의 경우 통행시간이 평균화되어 정보를 차량과 공유한다. Equilibrium의 평활화 계수는 1.0, Stochastic의 평활화 계수는 0.2로 주어진다.
| $$T_i^{n,k}=(1-\alpha)\times T_i^{n-1,k}+\alpha\times O_i^{n,k}$$ | (1) |
여기서, : 최종 통행시간
: 측정된 통행시간
: 평활화 계수
: 반복 횟수
: Simulation 내 분석 간격 시간
: Simulation 내 통행 구간(link)
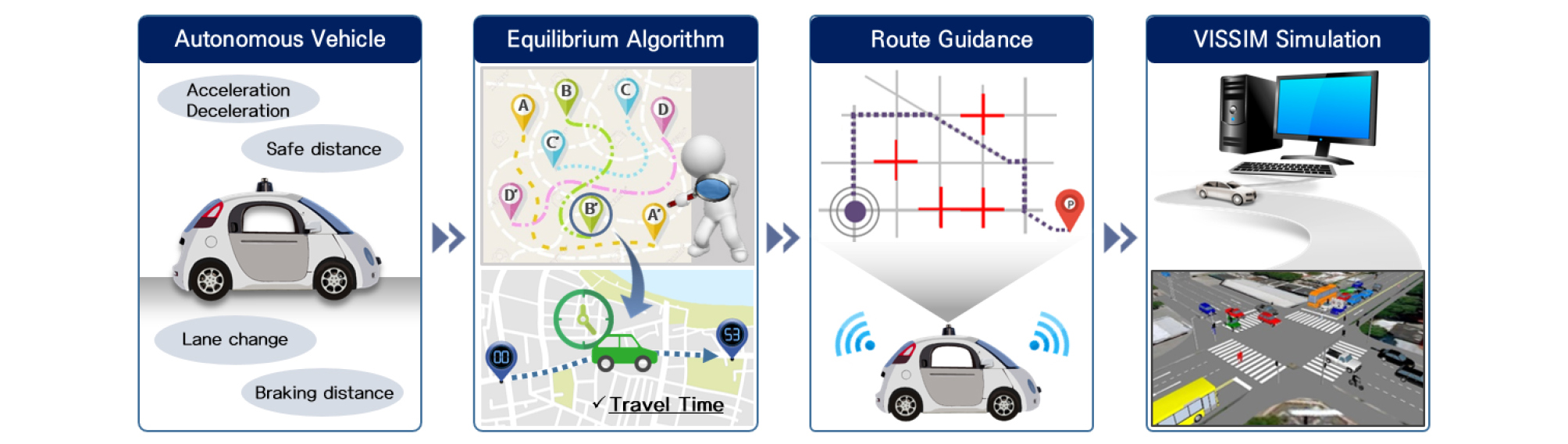
즉, 최적경로 탐색 시스템(DRGS)을 위한 동적 사용자 평행배정 기법(Dynamic User Equilibrium Assignment)은 Simulation 시간, 분석시간 간격, 차량 형태, 일반화비용 등의 다양한 파라미터를 고려한 알고리즘을 활용하여 효율적으로 Network 내 다양한 경로 선택을 유도하여 최적경로를 탐색하는 기법으로 도심부 내 시시각각으로 변화하는 교통상황에 따른 현실적인 교통 환경 구현이 가능하여 도로 혼잡상황, 요금체계 및 신호체계 등 다양한 시간 범위에 따라 적용하여 활용할 수 있다. 시뮬레이션 기반 최적경로를 탐색하는 동적 사용자 평행배정 기법(Dynamic User Equilibrium Assignment)의 과정을 Figure 3에서 제시하였다.
3) 경로탐색(Route Guidance) 알고리즘
경로탐색(Route Guidance)은 다양한 경로 중 일반화비용을 고려하여 경로를 선택하고 일정 시간 간격으로 교통상황을 판단하여 차량에게 경로를 안내하는 것이다. 일반화비용에는 통행시간(Travel Time), 통행거리(Travel Distance), 비용(Cost)으로 구성된다. 일반화비용 식은 Equation 2와 같다. 동적 사용자 평행배정 기법(Dynamic User Equilibrium Assignment) 기반 각 3가지 요인(통행시간, 통행거리, 비용)으로 자율주행차량(AV)과 연계하며, 여기서 통행비용(Cost)은 해당 Link의 km당 원가율과 일반 도로의 비용을 포함하여 계산되며, 통행시간(Travel Time)과는 달리 통행거리(Travel Distance)와 통행비용(Cost)의 경우 교통조건(기하구조, 통행료 등)에 영향을 받기 때문에 Simulation에 의해 결정되지 않는다.
대상지에서 발생하는 통행시간, 통행거리, 비용 등을 통해 모든 경로의 일반화비용을 계산하여 총 일반화비용()을 산정하고 이를 고려하여 출발지/도착지(O/D) 간 통행할 수 있는 다양한 경로 중 최적의 최단거리를 탐색한다. Equation 3과 같이 해당 경로 j에 대해서는 주행차량의 행동결정을 위해 Logit 모형을 활용하여 이용자가 경로 j를 선택할 확률() 산정 및 경로 j의 적정성을 판단한다.
| $$C_R=\sum_{a\in R}^{}C_a,\;U_j=\frac1{C_j},\;P(R_j)=\frac{e^{\delta U_j}}{\sum_{}^{}e^{\delta U_j}}$$ | (3) |
여기서, : 경로 j를 선택할 확률
: 경로 j의 이점
: 민감도 매개변수(Logit 모형)
여기서 일반화비용의 평균치보다 비용이 높으면 통행량이 감소하고 비용이 낮으면 통행량이 증가하도록 Equilibrium Assignment를 기반으로 교통수요를 재분배하도록 한다. Equation 4는 사전 교통량과 일반화비용을 통해 산정된 교통량이다.
| $$g_{s,n,v}^j=\gamma(g_{s-1,n,v}^j,\;c_{s,n,v}^j,\;\overline{c_{s,n,v}})$$ | (4) |
여기서, : 경로 j의 사전 Simulation의 교통량
: 경로 j의 일반화비용
: 평균 일반화비용
: 탐색 경로
: Simulation 시간
: 시간 간격
: 수단
Equastion 5는 각각의 출발지/도착지(O/D)에서 비용을 고려하여 간격마다 새롭게 산정된 경로 수 에 대해서 경로 j의 비용()과 평균 비용()을 통해 수요변화량()을 산정하여 재분배를 한다. 이러한 과정을 통해 주행차량은 다양한 경로 중 최적경로를 탐색하여 운행한다.
| $$c_s^j=c_{s,n,v}^j,\overline{\;c_s}=\sum_\widehat J^{}c_s^j=\frac1{\left|\widehat J\right|}\sum_{j\in\widehat J}^{}c_s^j,\;d_s^j=c_s^j-\overline{c_s}$$ | (5) |
여기서, : Simulation 시, 경로 j의 사전 수요변화량
: Simulation 시, 경로 j의 비용
: Simulation 시, 경로 j의 평균 비용
2. Simulation 구현방안
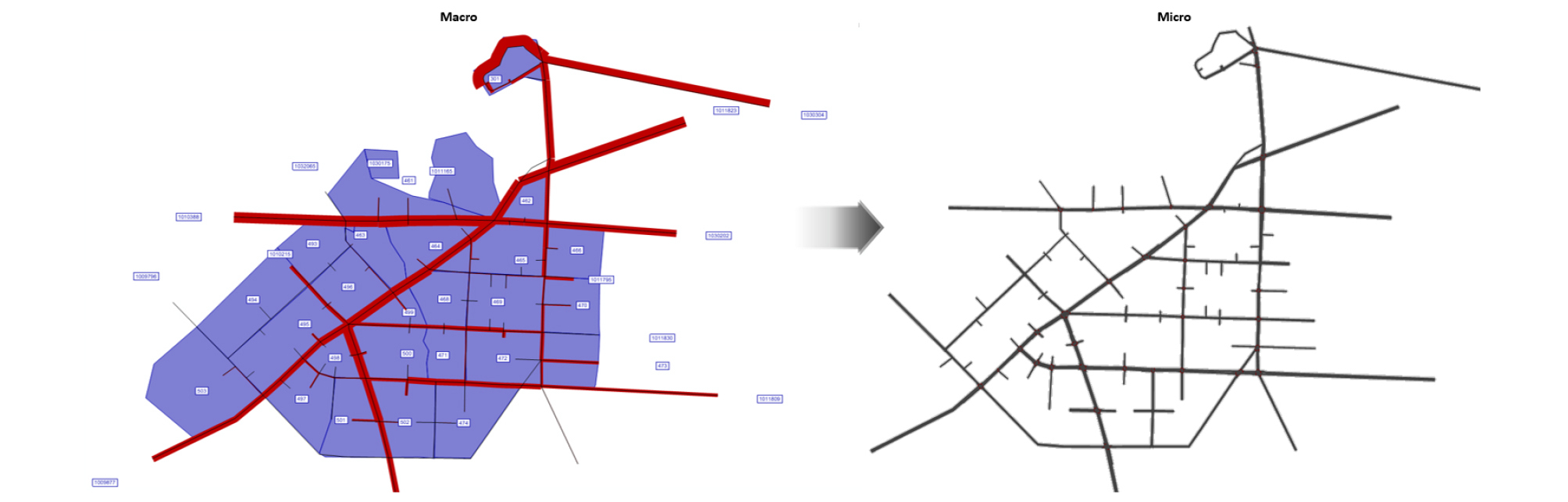
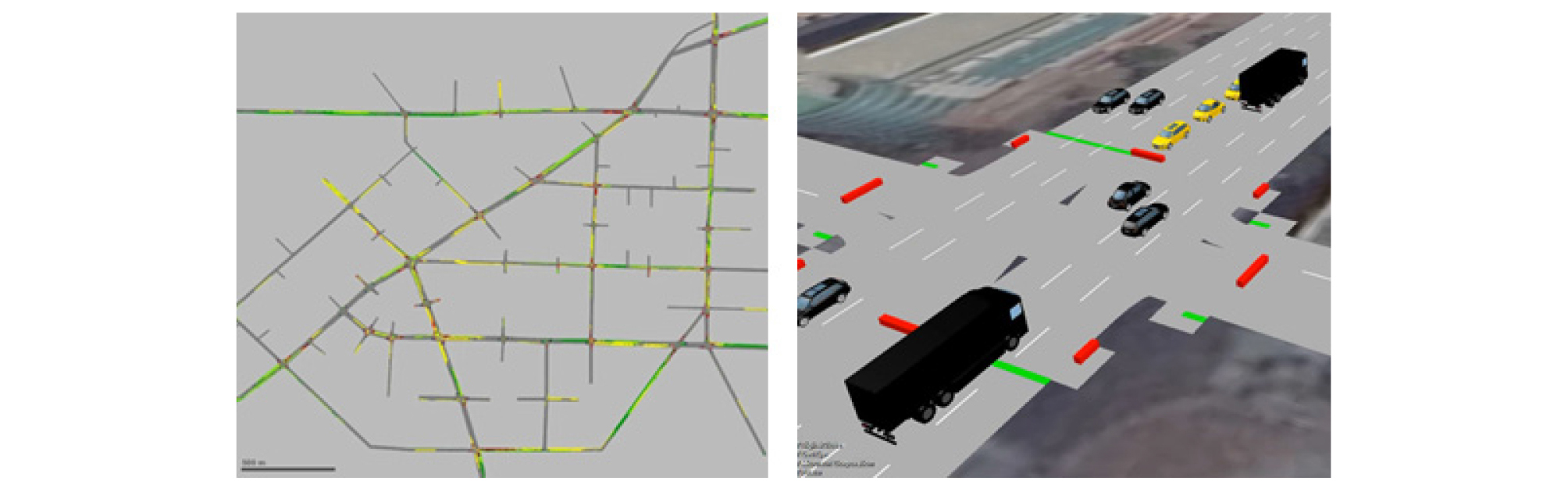
본 연구에서는 제주특별자치도 제주시 신제주를 대상으로 교통전문 Software인 교통수요 Macro Simulation 및 교통흐름 Micro Simulation을 활용하여 최적경로 탐색 시스템(DRGS)의 Simulation 구현에 따른 효과분석을 하고자 한다.
Figure 4와 같이 먼저 미시적(Micro) 측면의 교통흐름분석 모델인 VISSIM과 연계가 가능한 거시적(Macro) 측면의 교통수요분석 모델인 VISUM을 통해 Network 및 출발지/도착지(O/D) Matrix를 활용하였다. VISUM으로부터 Network 및 출발지/도착지(O/D) Matrix를 연계한 후 현실과 유사한 Network 구축 및 자율주행차량(AV) 등 개별 차량 특성을 고려하고 다양한 정량적 및 시각적 분석이 가능한 VISSIM을 활용하여 최적경로 탐색 시스템(DRGS) 도입에 따른 효과를 분석하고자 한다. 또한, 최적경로 탐색 시스템(DRGS)을 위해 VISSIM 내 통행배정(Assignment) 기법 및 경로탐색(Route Guidance) 파라미터를 설정하였다.
1) Simulation Network
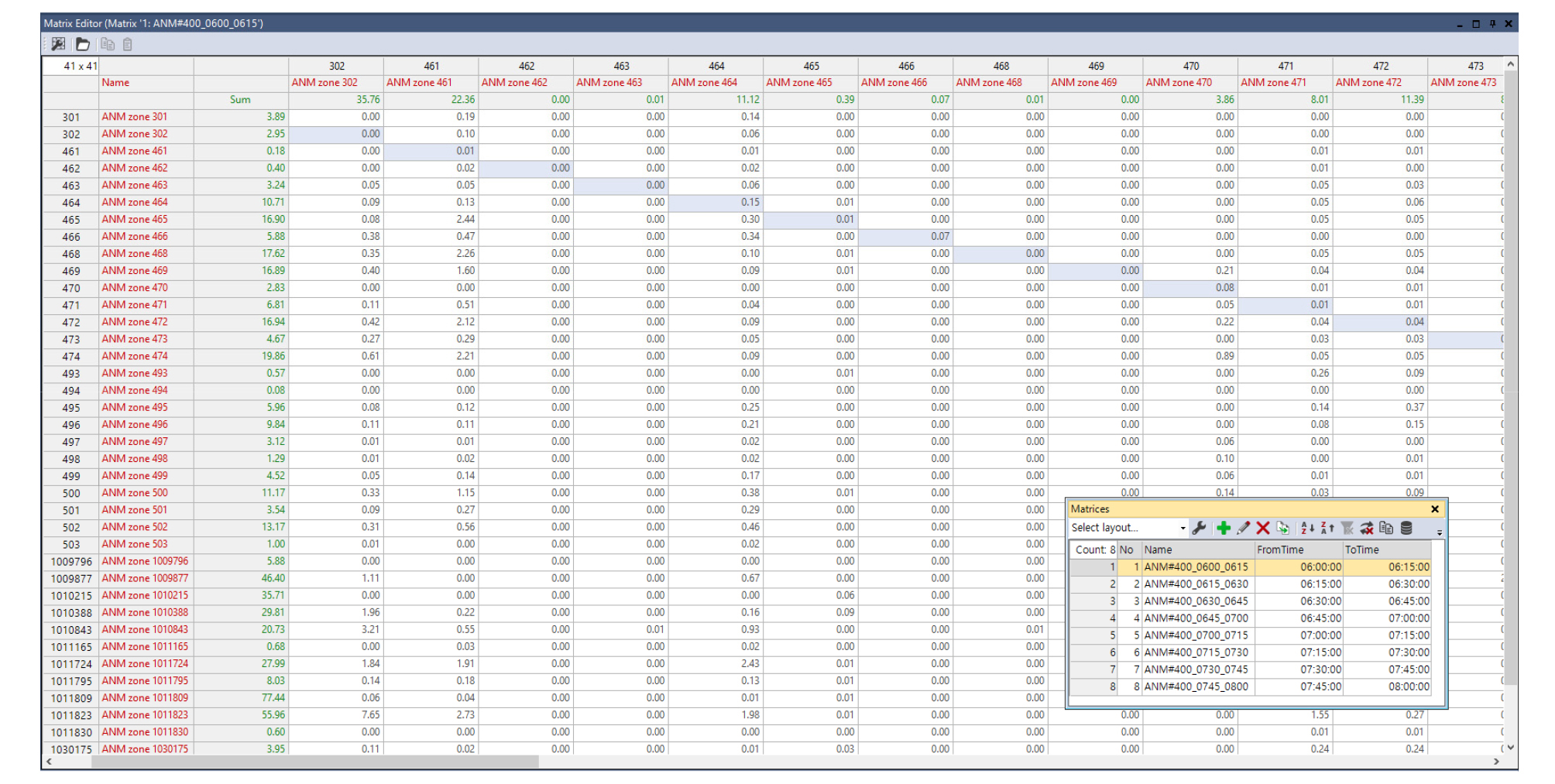
Simulation 구현을 위해 먼저 도로망(Link), 교통존(Zone), 기하구조(Geometry) 등이 구축되어있는 VISUM을 활용하여 기본 Network 및 시간대별 출발지/도착지(O/D) Matrix를 VISSIM에 연계하였으며, Figure 5에 연계된 Network를 제시하였고 해당 Network의 교통존(Zone) 정보, 15분 간격 출발지/도착지(O/D) Matrix를 Table 1과 Figure 6에 제시하였다.
Table 1. List of traffic zone
2) Assignment Parameter
Simulation 기반 시간대별 교통상황에 맞는 통행배정을 위해 동적 통행배정(Dynamic Assignment)을 수행하며, 통행배정 내 경로탐색을 위한 Volume (Standard) 기법, Stochastic 기법, Equilibrium 기법 중 이용자가 원하는 파라미터로 선정한다.
본 연구에서는 네트워크 내 차량의 통행시간(Travel Time)이 최소가 될 수 있도록 시간대별 O/D Matrix 기반의 경로탐색 반복과정을 통해 최적경로를 탐색하는 동적 사용자 평행배정 기법(Dynamic User Equilibrium Assignment)을 적용하였다.
3) Route Guidance Parameter
최적경로 탐색 시스템(DRGS)의 통행시간(Travel Time), 통행거리(Travel Distance), 비용(Cost)으로 구성된 Network 일반화비용 파라미터와 시스템을 적용할 차량을 연계하고 시스템 내 경로탐색(Route Guidance)의 경로탐색 전략(Strategy), 탐색시간 간격(Interval), 실행 소요시간(Offset)의 최적경로탐색 파라미터를 설정하였다.
Network 일반화비용 파라미터는 Simulation 기반의 동적 사용자 평행배정 기법(Dynamic User Equilibrium Assignment)과 관련하여 통행시간(Travel Time), 통행거리(Travel Distance), 비용(Cost)을 통해 Network의 비용을 산정하는 것으로 해당 통행배정(Assignment) 기법과 파라미터를 적용하는 개별 차량의 속성값을 변경하도록 한다.
Network의 통행배정(Assignment) 및 차량 유형(Vehicle Type) 설정 후 최적경로탐색 파라미터를 설정한다. 경로탐색 전략(Strategy)으로는 목적지에 따른 새로운 경로탐색 방법(전략 1)과 같은 교통존 내 새로운 목적지를 탐색하는 방법(전략 2)으로 구분되며, 본 연구에서는 출발지/목적지가 정해진 후 다양한 경로탐색을 하도록 전략 2를 적용하였다. 탐색시간 간격(Interval)은 Network 내 교통상황을 파악하여 일정 주기로 경로를 탐색하는 시간간격이며, 실행 소요시간(Offset)은 경로탐색 전략(Strategy)에 따른 탐색시간 간격(Interval)을 적용하였을 때, Figure 7처럼 Simulation 내 실제 수행되는 시간으로 최적경로 탐색 시 탐색시간 간격(Interval)과 실행 소요시간(Offset)을 다양하게 변경하여 최적경로 탐색 시스템(DRGS)의 효과분석이 가능하다.
3. Case Study
1) 분석 대상지 및 시나리오 설정
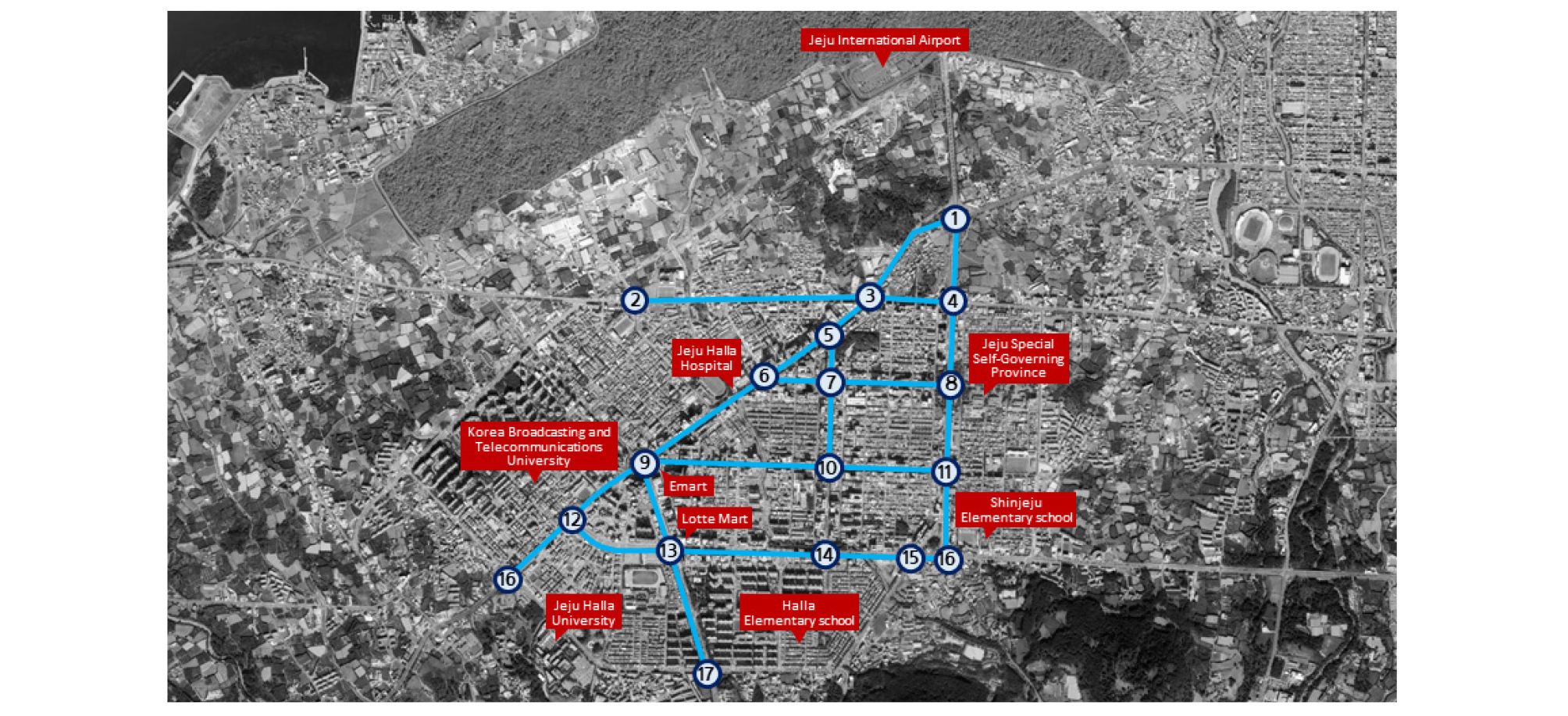
본 연구의 대상지는 관광객 및 차량 수요 급증으로 지속적으로 지 ‧ 정체가 발생하는 제주특별자치도 제주시 도심부 신제주로 Figure 8에 제시하였다. 현재 제주는 제주 통행특성이 반영된 교통수요/교통흐름/교통신호/대중교통/운영관리의 교통정책분석 시스템이 구축되어있으며, 신교통수단 자율주행차량(AV)의 효율적인 운영을 위한 Test-bed 환경이 조성되어 있다.
본 연구에서의 출발지/도착지(O/D)는 오라오거리부터 연동현대아파트 앞 교차로까지의 경로를 대상으로 오전 6시부터 8시까지 15분 간격으로 O/D Matrix를 설정하였으며, 시나리오 1은 최적경로 탐색 시스템(DRGS)의 동적 통행배정(Dynamic Assignment) 기반으로 Stochastic 기법과 Equilibrium 기법을 적용하였을 때를 구분하여 비교 분석하였으며, 시나리오 2는 최적경로 탐색 시스템(DRGS) 적용 여부에 따른 비교 분석을 수행하였다.
시나리오 1: 통행배정(Assignment) 비교 분석
시나리오 2: 최적경로 탐색 시스템(DRGS) 적용 효과분석
2) 시나리오 효과분석 결과
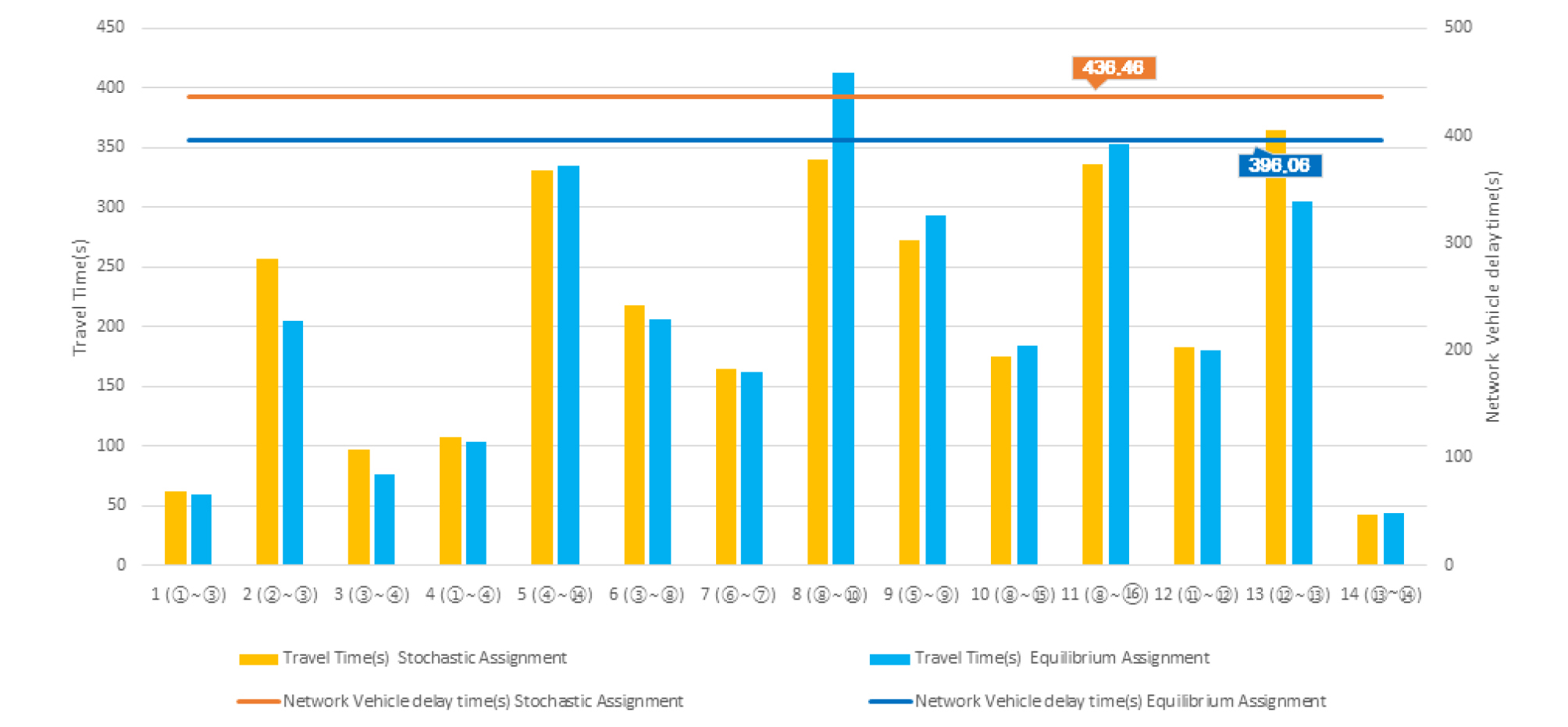
먼저 신제주 Network를 대상으로 통행배정(Assignment) 기법 중 Stochastic 기법과 Equilibrium 기법을 적용하여 구간별 통행시간(Travel Time)과 Network 내 통행하는 차량 당 평균 지체시간(Network Vehicle Delay time)을 비교 분석하였으며, Table 2에 제시하였다.
Table 2. List of comparative analysis of assignment (quantitative indicator)
Stochastic Assignment를 적용하였을 때, 구간 5, 8, 9, 10, 11을 제외하고 Equilibrium Assignment를 적용하였을 때보다 통행시간(Travel Time)이 증가하였다. 특히, Network 내 통행하는 차량 당 평균 지체시간(Network Vehicle Delay time)은 396.06초에서 436.46초로 40.4초(약 10.2%) 증가한 것으로 분석되었다.
Figure 9와 같이 Network 내 구간별 통행시간(Travel Time)과 Network의 평균 지체시간을 비교 분석한 결과, 일반화비용을 고려하여 모든 경로를 다양하게 탐색하는 Stochastic Assignment보다 교통수요 재분배로 통행시간(Travel Time)이 최소화되도록 하는 Equilibrium Assignment를 활용하는 것이 적정하다고 판단되었다.
최적경로 탐색 시스템(DRGS) 적용 효과분석을 위해 Simulation의 Route Guidance Parameter를 탐색시간 간격(Interval) 180초, 실행 소요시간(Offset) 60초로 설정하였다.
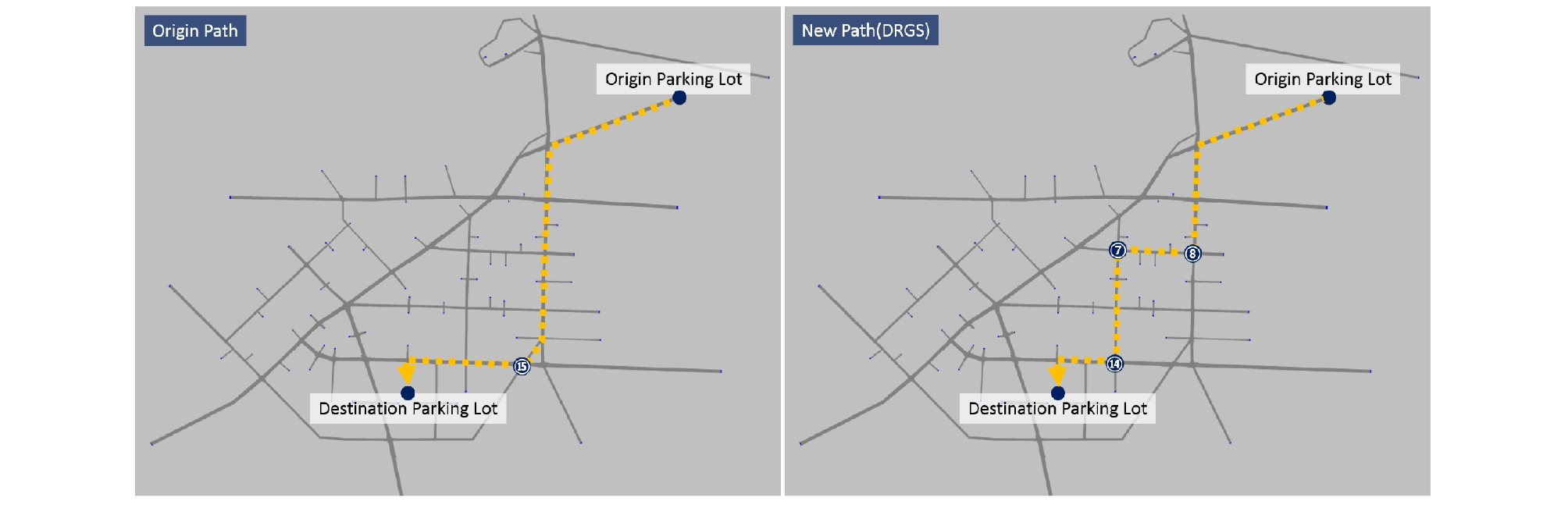
주어진 경로(오라오거리-연동현대아파트 앞 교차로)에서 기존 경로의 경우 신제주로터리(⑧)에서 직진한 후 신시가지입구교차로(⑮)에서 우회전하는 경로로 통행하나 최적경로 탐색 시스템(DRGS) 기반 신규 경로의 경우 신제주로터리(⑧)에서 우회전 후 삼무공원사거리(⑦)에서 좌회전하며, 대림아파트 앞 교차로(⑭)에서 우회전하는 경로로 통행하는 것으로 분석되었다(Figure 10).
즉, 기존 경로와 비교하였을 때, 최적경로 탐색 시스템(DRGS)을 적용한 신규 경로는 기존 경로 구간에 교통상황 및 신호체계에 따라 통행시간과 대기시간이 증가하여 우회하여 통행하는 것으로 분석되었다.
Table 3과 같이 오라오거리부터 연동현대아파트 앞 교차로까지 차량이 통행하였을 때, 기존 경로의 경우 13회의 정지와 593.30초의 대기시간으로 780.96초의 지체시간이 발생하였으며, 최적경로 탐색 시스템(DRGS) 기반 신규 경로의 경우 6회의 정지와 427.50초 대기시간으로 578.80초의 지체시간이 발생하였다. 최적경로 탐색 시스템(DRGS)을 적용하였을 때, 기존 경로에 비해 지체시간이 약 25.9%(-202.16초) 감소한 것으로 분석되었다.
Table 3. List of comparative analysis of DRGS application
| Division | Origin path | New path | Increase/Decrease |
| Delay time (s) | 780.96 | 578.80 | -202.16 |
| Waiting time (s) | 593.30 | 427.50 | -165.80 |
| Stops (number) | 13 | 6 | -7 |
| Network vehicle time (s) | 439.55 | 396.06 | -43.49 |
또한, Network 내 통행하는 차량 당 평균 지체시간(Network Vehicle Delay time)을 비교 분석한 결과로는 439.55초에서 396.06초로 43.49초(약 9.9%) 감소한 것으로 최적경로 탐색 시스템(DRGS)의 효과를 제시하였다.
결론
본 연구는 자율주행차량(AV)의 단계별 도입에 앞서 효율적인 운행을 위한 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS)을 제시하였다. Simulation 기반의 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS) 내 다양한 통행배정(Assignment) 및 경로탐색(Path Search)을 통해 자율주행차량(AV) 이용자들에게 어떠한 영향을 미치는 지를 알아보고자 하였다.
본 연구에서는 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS)의 동적 통행배정(Dynamic Assignment) 기법 중 Stochastic Assignment와 Equilibrium Assignment 적용에 따른 구간별 통행시간(Travel Time) 비교 분석을 수행하였으며, Route Guidance의 다양한 파라미터(Travel Time, Travel Distance, Cost, Interval, Offset)를 설정하여 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS) 적용의 효과분석 결과를 제시하였다.
제주특별자치도 제주시 신제주를 대상으로 Network 차원의 경로탐색 결과를 비교 분석하였을 때, Stochastic Assignment 적용 시 보다 Equilibrium Assignment 적용 시 구간별 통행시간(Travel Time) 및 Network 내 통행하는 차량 당 평균 지체시간(Network Vehicle Delay time)이 감소되었으며, 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS) 적용 여부에 따른 효과분석 시 교통상황 혼잡 시 기존 경로와 비교하여 다른 경로로 우회함으로써 지체시간(Delay time) 및 대기시간(Waiting time)이 감소하였다. 통행시간(Travel Time) 최소화를 위한 Equilibrium Assignment 및 Route Guidance에 의해 지체시간(Delay time) 및 대기시간(Waiting time)의 감소로 도심부의 원활한 교통흐름을 기대할 수 있으며, Simulation 기반의 최적경로 탐색 시스템(Dynamic Route Guidance system, DRGS)을 실질적으로 도심지에 적용하고자 할 때의 구축방안 및 향후 연구방향을 제시하고자 한다.
첫째, 실제 도로에서 수집 가능한 교통 데이터(도로망, 교통량, 통행속도, 통행시간 등)를 활용하여 다양한 교통상황 분석으로 자율주행차량(AV)이 운행 시 겪을 수 있는 모든 상황들에 대한 시나리오를 정립하여야 한다. 즉, 과거이력데이터 활용 또는 자율주행차량(AV)의 사전 도로주행으로 인공지능(AI) 학습을 통한 경로탐색이 이뤄져야 한다.
둘째, 사람이 운전하지 않아도 자율주행차량(AV)이 스스로 도로를 주행할 수 있도록 적정 가 ‧ 감속도 설정 및 차량 간 안전거리, 장애물에 따른 시거 확보, 차선유지 등 교통 환경에 따른 자율주행차량(AV)의 파라미터를 설정해야한다. 현재 자율주행차량(AV)이 단계별로 구분되어 있어 이를 고려한 파라미터를 활용하여 경로탐색 시 원활한 주행이 가능하도록 해야 한다.
셋째, 실제 도로에서 자율주행차량(AV)은 기존에 입력되어있는 프로그램을 기반으로 주행하기 때문에 도로 사정에 따른 다양한 변수(Spill-back 등)에 대해 반영하기가 어려워 효율적이고 원활한 자율주행차량(AV)의 운영을 위해 사전 다양한 교통상황별 Simulation 시나리오 분석 및 Test-bed 구축이 필요하다.
넷째, 자율주행차량(AV)의 V2X 기능 구현을 위해 자율주행차량(AV) 내 첨단센서를 활용하여 교통정보센터와 교통상황(인프라, 차량, 보행자 등)에 대한 교통정보를 수집하며, 차량 간 수집 데이터를 공유함으로써 주변 상황에 따라 자신의 상태를 변경하여 효율적인 운행을 함으로써 모든 차량이 최적경로로 통행이 가능하도록 한다.
향후 연구방안으로는 도심부에 존재하는 다양한 교통상황 분석과 자율주행차량(AV) 도입으로 인한 교통체계 운영을 Network 차원의 교통관리 및 신호체계 전략이 필요하며, 이를 위해 교통정보센터 데이터를 활용하여 자율주행차량(AV)에게 제공하고 자율주행차량(AV)의 군집 형성을 고려한 교차로 및 교통축 차원의 신호체계가 필요하다.