서론
방법론
1. 기본 모형
2. 교통수단별 최적 가격, 최적 점유율 모형
고속철도의 경쟁전략 요소에 따른 영향 분석
연구모형의 서울-부산 노선에 대한 적용
1. 서울-부산 노선의 실제 자료를 통한 모형 결과 추정
2. 서울-부산 노선의 실제 자료와 추정모형 값의 비교분석
시사점
결론
서론
고속철도(High-speed rail)는 1964년 도쿄에서 처음 운행되었으며, 이후 영국을 시작으로 프랑스, 스페인을 비롯한 여러 유럽국가에서 운행되고 있는 중이다. 국내의 경우 2004년 서울-대구 노선을 시작으로 현재까지 계속해서 노선을 확장해가는 과정 중에 있다. 고속철도의 확장과 기술 발전은 항공 교통시장에도 큰 변화를 가져다주었다. 고속철도의 도입으로 인해 항공수요가 감소했고, 항공사가 이에 대응하기 위해 가격 경쟁, 노선 경쟁, 전서비스항공사(full service carrier, FSC)의 저비용항공사(low cost carrier, LCC)설립 등 다양한 전략을 시행함에 따라 본격적으로 고속철도와 항공사간의 경쟁구도가 형성되었다. 이러한 상황에 따라 국내 ‧ 외 학계에서도 고속철도와 항공사의 경쟁관계에 관련된 연구가 꾸준히 진행되어 왔다. 기본적인 회귀방정식에서부터 다양한 종류의 방법론이 활용되었으며, 연구 범위 또한 좁게는 하나의 노선, 넓게는 국가나 연합에 이르기까지 다양한 연구가 존재한다.
Adler et al.(2010)는 게임이론을 활용하여 가격, 운항횟수, 고속철도와 항공기의 규모 등의 변수를 중점으로 유럽 지역의 네트워크 최적화 분석을 수행하였다. Albalate et al.(2015)는 좌석 수와 운항횟수를 변수로 활용한 Supply oriented empirical analysis를 통해, 고속철도로 인해 항공사의 좌석은 감소하며, 운항 횟수에는 영향을 받지 않는다고 분석하였다. Behrens and Pels(2012)은 2003년부터 2009년까지의 런던-파리 노선의 승객 수요를 Multinomoial and mixed logit model을 활용하여 비교 분석하였다. Castillo-Manzano et al.(2015)는 스페인 국가의 항공승객과 고속철도 승객 수와 신규 고속철도 노선의 개통 일정, 신규 공항의 개통 일정 등을 변수로 설정한 Dynamic Linear Regression을 방법론으로 사용하여 고속철도의 네트워크 확장이 스페인 항공 교통시장에 미치는 영향에 대하여 추정하였다. Román et al.(2007)는 마드리드-바르셀로나 노선에 국한하여 여행 시간, 대기 시간, 지연 시간 등의 시간적 변수를 활용하여 연구를 진행하였으며, 그 결과 고속철도가 항공사에 비해 WTP (willing to pay)가 높으며 단거리 노선일수록 고속철도가 경쟁적이라고 판단하였다. D’Alfonso et al.(2015)는 Duopoly model을 활용하여 환경적 측면과 사회적 복지 측면에서 항공사와 고속철도를 비교분석 시행하였다. 또한 D’Alfonso et al.(2016)는 앞선 선행연구를 통해 런던-파리 노선의 시장에서 시뮬레이션 연구를 수행하였다. 이를 통해 런던-파리노선에서 고속철도의 사회적 복지 비중이 높아질수록 환경에 부정적 영향을 끼칠 가능성이 크다는 결론을 도출하였다. Fu et al.(2012)는 연구를 통해 고속철도의 경우 중국에서 네트워크 연결성, 총 여행시간, 가격 효율 등의 이유로 매우 경쟁성이 높다고 판단하였으며, 반면 중국 내 항공시장의 경우 항공 수요의 지역불균형, 공항 내 수용성, 항공사 네트워크의 발전가능성 등의 이유로 매우 불균형적인 상태로 판단하였다. Park et al.(2004)는 국내에서 고속철도가 운항을 시작하면서 항공사에 미치는 영향을 Stated Preference survey를 활용하여 분석하였다. Lim et al.(2008)는 LCC진입이 국내 교통수단 선택에 주는 영향을 Binary Logit model과 Stated Preference survey를 활용하여 분석하였다. Yang and Zhang(2012)는 Hotelling model을 활용하여 중국 내의 고속철도와 항공사간의 경쟁관계를 가격, 수익, 사회적 복지 관점에서 연구하였다. 또한 일반 여행 승객과 비즈니스 승객으로 구분하여 연구를 진행하였다.
이와 같이 다양한 방법론을 활용하여 항공사와 고속철도와의 경쟁관계에 대한 연구를 진행하였으나, 대다수의 선행연구들은 항공 교통수단을 하나의 교통수단으로 판단하거나, 항공 교통수단 중에서 FSC 또는 LCC에서 하나를 선택하여 이와 고속철도와의 관계를 분석하는 연구를 진행하였다. 하지만 LCC는 항공사의 운영비용을 줄이고 이를 통해 더욱 저렴한 티켓 가격을 제공함으로써 FSC보다 더 대중적인 성격을 가지고 있기 때문에, 본 연구에서는 기존 선행연구와는 다르게 항공 교통수단을 FSC와 LCC로 구분하여 실제 교통시장 상황을 더 정확하게 반영한 연구를 진행하였다.
본 연구는 비교 분석을 위해서 Salop(1979)의 Circular city model을 활용하여 고속철도와 FSC, LCC 세 교통수단 간의 최적 가격과 점유율을 추정하는 모형을 개발하였고, 교통수단 간의 경쟁관계를 모형으로 나타냄으로써 고속철도의 경쟁전략 요소(사회적 후생수준 고려 정도, 고속철도의 속도와 터미널로의 접근시간)로 인해 각 교통시장의 운임과 점유율이 어떻게 변화하는지 분석하였다. 또한 본 연구에서는 국내에서 가장 수요가 많은 노선 중 하나인 서울-부산 노선의 실제 자료를 개발 모형에 적용함으로써 1)각 교통수단의 최적 가격과 점유율을 파악하고, 2)추정된 최적 가격과 점유율을 서울-부산 노선의 2011년부터 2016년까지의 세 가지 교통수단의 실제 가격과 점유율과 비교 분석하였다. 기존 선행연구들이 회귀분석 등의 다양한 방법론을 통해 특정 지역이나 노선에 대하여서만 고속철도와 항공사간의 관계를 분석하는 반면, 본 연구의 Circular city model을 활용한 개발 모형은 서울-부산 노선뿐만 아니라 다양한 노선에 적용할 수 있으며 활용도가 높다는 점에서 의의를 가진다.
방법론
1. 기본 모형
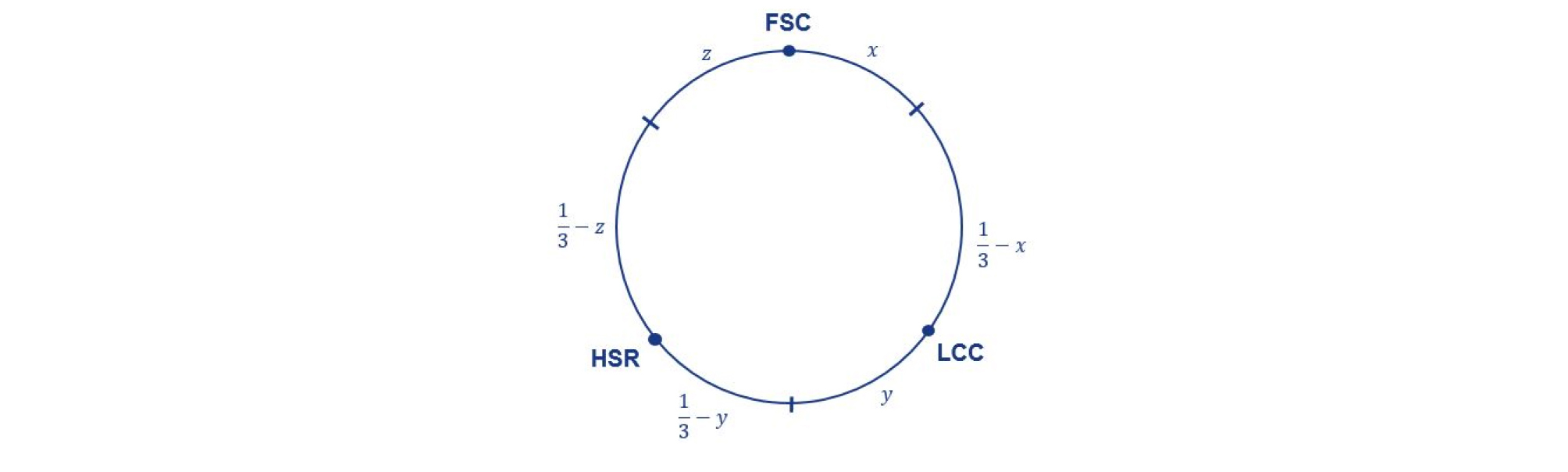
앞서 말한 Yang and Zhang(2012)의 선행연구와 같이 많은 논문들이 수단선택의 문제에서 게임이론의 고전적인 모형 가운데 하나인 Hotelling model을 사용하고 있다. 하지만 Hotelling model은 길이가 1인 모든 소비자들이 균등하게 분포하여있는 선형공간의 양 쪽 끝에 공급자를 설정하여 분석을 진행하기 때문에, 두 공급자간의 경쟁만을 분석할 수밖에 없다는 단점을 가지고 있다. 본 연구는 선형이 아닌 원형의 공간에 공급자가 위치한다고 가정함으로써, 두 개 이상의 공급자들을 비교 분석가능하게 만든 circular city model을 활용하여 세 가지 교통수단의 경쟁관계와 점유율을 추정할 수 있는 모형 Figure 1을 설정하였다.
본 연구에 활용되는 변수들에 대하여 정리한 Table 1은 다음과 같다.
Table 1. Summary of notations
모형에서 소비자는 소비자의 전체효용(b)에서 이동비용과 각 시장의 가격(pi)을 제한 값이 0보다 큰 경우에 한하여, 소비자의 효용이 더 큰 교통수단을 선택하게 된다. 본 연구에서는 이동비용을 총 여행시간(ji)과 소비자의 시간가치(v)를 곱한 값과 그 외 비효율변수(t)로 구성하였다. 비효율 변수란 시간가치(v)외의 다른 선택요인이 되는 안정성과 편리성을 예로 들 수 있다. 또한 총 여행시간은 Equation 1로 구성되어 있다.
| $$j_i=\alpha_i+\frac{l_i}{s_i}+\frac{T_i}{4f_i}$$ | (1) |
αi는 교통수단 i의 접근시간(Access time)을 의미하며 li/si는 총 여행거리/속도로 실제 여행시간을 나타낸다. Ti/4fi는 예상되는 지연시간을 의미한다. 이는 Brueckner(2004)와 Brueckner and Flores-Fillol(2007) 연구의 변수를 활용한 것이다.
모형에선 둘레가 1인 원을 3등분하여 각각의 교통수단이 경쟁하는 시장을 일반항공(full service carrier, FSC)과 저비용항공(low cost carrier, LCC), 고속철도와 저비용항공(LCC), 고속철도와 일반항공(FSC) 총 세 가지의 경쟁시장으로 나타내었으며, FSC가 LCC와의 경쟁시장에서 차지하는 점유율(x), LCC가 고속철도와의 경쟁시장에서 차지하는 점유율(y), FSC가 고속철도와의 경쟁시장에서 차지하는 점유율(z)과 개별 경쟁시장의 최대 점유율인 에서 x, y, z를 빼준 값을 통하여 각 교통수단의 점유율을 Equations 2-4와 같이 표현하였다.
고속철도의 점유율(Market share)
| $$D_H=\frac23-(y+z)$$ | (2) |
FSC의 점유율(Market share)
| $$D_F=x+z$$ | (3) |
LCC의 점유율(Market share)
| $$D_L=\frac13-x+y$$ | (4) |
또한 모형 Figure 1에서 각 교통수단이 차지하는 점유율의 경계선에 위치한 균형점은 소비자 효용에서 다른 비용을 뺀 값이 동일한 소비자들을 나타내며, 이 위치에 있는 소비자는 두 교통수단을 선택하는 선호도가 동일하다고 할 수 있다. 이 점을 활용하여 각각의 경쟁 시장의 Equations 5-7을 나타내었다.
Market 1. FSC와 LCC의 경쟁 시장
| $$b-p_F-v\cdot j_F-t\cdot x=b-p_L-v\cdot j_L-t\left(\frac13-x\right)\geq0$$ | (5) |
Market 2. 고속철도와 LCC의 경쟁 시장
| $$b-p_L-v\cdot j_L-t\cdot y=b-p_H-v\cdot j_H-t\left(\frac13-y\right)\geq0$$ | (6) |
Market 3. 고속철도와 FSC의 경쟁 시장
| $$b-p_F-v\cdot j_F-t\cdot z=b-p_H-v\cdot j_H-t\;\left(\frac13-z\right)\geq0$$ | (7) |
다음으로 각 교통수단의 Profit을 식으로 나타내는 과정을 가진다. 고속철도, FSC, LCC의 수익은 Equations 8-10으로 나타낼 수 있다.
고속철도의 수익
| $$\pi_H=(p_H-c_H)D_H-f_H\cdot K_H$$ | (8) |
FSC의 수익
| $$\pi_F=(p_F-c_F)D_F-f_F\cdot K_F$$ | (9) |
LCC의 수익
| $$\pi_L=(p_L-c_L)D_L-f_L\cdot K_L$$ | (10) |
공기업이 운영하는 고속철도의 경우 항공교통수단과는 달리 수익을 추구하는 동시에 사회적 후생을 추구해야 한다. 사회적 후생을 과도하게 추구 할 경우 수익창출을 통한 가치극대화가 불가능해지는 반면, 수익만을 과도하게 추구할 경우 공공성 및 사회적 편익을 유지할 수 없기에, 고속철도의 입장에서 사회적 후생 창출에 어느 정도 비중을 두느냐가 중요한 관건이 될 것이다. 이를 분석하기 위해 본 연구에서는 θ(사회적 후생수준 고려 정도)를 활용하여 고속철도가 사회적 후생(Social welfare)과 수익성(Profit)을 모두 고려하도록 모형을 설정하였으며 θ(사회적 후생수준 고려 정도)의 변화가 각 경쟁시장에 주는 영향을 분석하였다. 먼저 고속철도의 승객들의 소비자 잉여(consumer surplus)를 나타내는 식을 도출하였으며, 이를 통해 고속철도의 사회적 후생을 식으로 나타내었다. 이후, 사회적 후생과 고속철도 수익의 가중합(Weighted sum of welfare and profit)을 식으로 도출하였다. 앞서 말한 식은 Equations 11-13과 같다.
고속철도 승객의 소비자 잉여
| $$CS_H=\int_y^\frac13{\left(b-p_H-v\cdot j_H-t\;\left(\frac13-\alpha\right)\right)d\alpha+\int_z^\frac13{\left(b-p_H-v\cdot j_H-t\;\left(\frac13-\beta\right)\right)d\beta}}$$ | (11) |
고속철도의 사회적 후생
| $$W_H=\pi_H+CS_H$$ | (12) |
사회적 후생과 고속철도 수익의 가중합
| $$\theta W_H+(1-\theta)\pi_H$$ | (13) |
2. 교통수단별 최적 가격, 최적 점유율 모형
위의 과정을 통해 추정된 식을 활용하여 각 교통수단의 최적 가격과 최적 점유율에 대한 식을 도출하였다. 먼저 FSC와 LCC의 목적인 수익과 고속철도의 목적인 사회적 후생과 고속철도 수익의 가중합(Weighted sum of welfare and profit)에서 각 운송수단의 가격(ptransport mode)로 1차 미분하는 과정을 통해 각 교통수단의 최적 운임(p*transport mode)에 대한 식을 도출해낼 수 있다. 이 과정은 다음과 같다.
고속철도의 경우 도출과정
| $$\frac{\sigma\;(\theta CS_H+\pi_H)}{\sigma p_H}=\frac\theta{12}(-3(p_F+p_L-6p_H)-12b-3v(j_F+j_L-6j_H)-2t)+\frac1{6t}(3(p_F+p_L-4p_H)+3v(j_F+j_L-2j_H)+6C_H+2t)=0$$ | (14) |
FSC의 경우 도출과정
| $$\frac{\sigma\pi_F}{\sigma p_F}=\frac{3(p_L+p_H-4p_F)+3v(j_H+j_L-2j_F)+6C_F+2t}{6t}=0$$ | (15) |
LCC의 경우 도출과정
| $$\frac{\sigma\pi_L}{\sigma p_L}=\frac{3(p_F+p_H-4p_L)+3v(j_F+j_H-2j_L)+6C_L+2t}{6t}=0$$ | (16) |
최종적으로 도출되는 각 교통수단의 최적 운임(Optimal price)은 Equations 17-19로 나타낼 수 있다.
고속철도의 최적 운임 도출식
| $$p_H^\ast=\frac1{60-49\theta}\;(\;18C_H-42C_F-6C_L+6v(8j_F-j_L-7j_H)\;-10t-\theta(\frac25(14C_L+11C_F)+\frac15v(7j_F+28j_L-245j_H)+36b+\frac{28}3t\;))$$ | (17) |
FSC의 최적 운임 도출식
| $$p_F^\ast=\frac1{60-49\theta}(18C_F+6C_L+6C_H+6v(j_L-2j_F+j_H)+10t-\theta(\frac25(21C_L+69C_F)+\frac25v(21j_L-56j_F)+12b+14t\;))$$ | (18) |
LCC의 최적 운임 도출식
| $$p_L^\ast=\frac1{60-49\theta}(30C_L-6C_F+6C_H+6v(4j_F-5j_L+j_H)+10t-\theta(28C_L+8C_F+v(7j_F-21j_L)+12b+14t))$$ | (19) |
교통수단의 최적운임(Optimal price)의 식을 그대로 활용하여, 각 경쟁시장 Equation 5-7 식을 x,y,z에 대해 정리한 식에 대입하는 과정을 통해 세 가지 시장의 최적 균형점인 x*,y*,z*을 도출하였다. 도출한 최적 균형점은 Equations 20-22로 나타낼 수 있다.
FSC와 LCC 경쟁 시장에서의 균형점
| $$x^\ast=\frac1{60-49\theta}(12(C_L-C_F)+12v(j_L-j_F)+10t-\theta(\;\frac{49}5(C_L-C_F)+\frac{49}5v(j_L-j_F)+\frac{49}6t))$$ | (20) |
고속철도와 LCC 경쟁 시장에서 균형점
| $$y^\ast=\frac1{60-49\theta}(6(C_H-3C_F-3C_L)+6v(2j_F-3j_L+j_H)-\theta(\frac{1\;}5(-56C_L-9C_F)+\frac15v(-14j_F-56jL)+12b+\frac56t))$$ | (21) |
고속철도와 FSC 경쟁 시장에서 균형점
| $$z^\ast=\frac1{60-49\theta}(6(C_H-5C_F-3C_L)+6v(j_H-j_L)-\theta(\frac15(-58C_F-7C_L)+\frac15v(-63j_F-7j_L)+12b+\frac{35}6t))$$ | (22) |
위의 최적 균형점 Equations 20-22를 앞서 Circular city model을 활용하여 도출한 Equations 2-4에 대입하면 각 교통수단의 최적 점유율(Market share)의 식 또한 도출할 수 있다.
고속철도의 경쟁전략 요소에 따른 영향 분석
개발 모형을 통해 고속철도의 경쟁전략(사회적 후생수준 고려 정도, 접근시간, 속도)에 따른 최적 가격과 점유율의 변화를 분석함으로써, 변수들이 각 교통수단 시장에 어떠한 영향을 미치는지를 분석하고자 한다.
Proposition 1.
고속철도가 사회적 후생수준 고려 정도(θ) 비중을 늘릴수록 모든 교통수단의 티켓 가격은 감소한다.
이에 대한 증명과정은 다음과 같다.
Proof.
| $$\frac{\sigma p_H^\ast}{\sigma\theta}=3\frac{\sigma p_F^\ast}{\sigma\theta}+\frac{6^\circ147C_H}{(60-49\theta)^2}\leq0$$ | (23) |
| $$\frac{\sigma p_F^\ast}{\sigma\theta}\leq0$$ | (24) |
| $$\frac{\sigma p_L^\ast}{\sigma\theta}=\frac{\sigma p_F^\ast}{\sigma\theta}\leq0$$ | (25) |
각 교통수단의 최적운임을 나타내는 Equations 23-25를 사회적 후생수준 고려 정도(θ)로 1차미분한 결과, 최적운임과 관련된 Equations 23-25 모두 0보다 작으므로 θ가 증가함에 따라 모든 교통수단의 최적가격도 감소함을 알 수 있다. 이를 통해 사회적 후생수준 고려 정도(θ)의 증가는 세 종류의 교통수단 간의 경쟁을 더욱 심화시키며, 이로 인해 모든 교통수단의 티켓 가격이 감소함을 알 수 있다.
Proposition 2.
고속철도가 사회적 후생수준 고려 정도(θ) 비중을 늘릴수록 고속철도의 점유율은 증가하는 한편 FSC와 LCC의 점유율은 감소한다.
이에 대한 증명과정은 다음과 같다.
Proof.
| $$\frac{\sigma x^\ast}{\sigma\theta}=0$$ | (26) |
| $$\frac{\sigma y_{}^\ast}{\sigma\theta}\leq0$$ | (27) |
| $$\frac{\sigma z_{}^\ast}{\sigma\theta}=\frac{\sigma y_{}^\ast}{\sigma\theta}-\frac{300t}{(60-49theta)^2}\leq0$$ | (28) |
각 교통수단의 점유율을 도출해낼 수 있는 Equations 20-22를 사회적 후생수준 고려 정도(θ)로 1차 미분한 결과, 항공수단의 점유율과 관련된 Equations 27, 28이 0보다 작고 Equation 28이 Equation 27보다 더 작으므로 사회적 후생수준 고려 정도(θ)가 증가할수록 FSC의 점유율이 LCC의 점유율보다 더욱 민감하게 떨어짐을 확인할 수 있다. Equation 26의 값이 0이기에 변동이 없다고 생각 할 수도 있지만 FSC와 LCC의 점유율이 떨어지면 결과적으로는 고속철도의 점유율이 증가할 것 이다. 이를 통해 사회적 후생수준 고려 정도(θ)가 증가하면 고속철도의 경쟁력이 강화되기에, 고속철도가 FSC와 LCC에 경쟁하는 시장에서 점유율을 가져오게 됨을 알 수 있다.
Proposition 3.
(ⅰ) 고속철도의 티켓가격의 경우 사회적 후생수준 고려 정도(θ)의 수준이 ‘’의 경우에 고속철도의 티켓가격은 고속철도 터미널의 접근시간(αH)이 증가할수록 감소하게 된다.
(ⅱ) 고속철도 터미널의 접근시간(αH)이 증가할수록 FSC와 LCC의 티켓가격이 증가한다.
이에 대한 증명과정은 다음과 같다.
Proof.
| $$\frac{\sigma p_H^\ast}{\sigma\alpha_H}=\frac{-7v}{(60-49\theta)}(6-7\theta)$$ | (29) |
| $$\frac{\sigma p_F^\ast}{\sigma\alpha_H}=\frac{6v}{(60-49\theta)}>0$$ | (30) |
| $$\frac{\sigma p_L^\ast}{\sigma\alpha_H}=\frac{6v}{(60-49\theta)}>0$$ | (31) |
각 교통수단의 최적운임을 나타내는 Equations 17-19를 고속철도 터미널의 접근시간(αH)으로 1차미분한 결과, 고속철도 터미널의 접근시간(αH)의 변화와 고속철도의 티켓가격은 사회적 후생수준 고려 정도(θ)의 수준이 ‘’의 경우에는 음의 관계를, ‘’의 경우에는 양의관계를 가짐을 Equation 29를 통해서 알 수 있다. Equations 30, 31을 통해 FSC와 LCC의 티켓가격의 경우에는 고속철도 터미널의 접근시간(αH)이 증가할수록 함께 증가함을 확인 할 수 있다. 이를 통해 고속철도 터미널의 접근시간(αH)이 증가할수록 FSC와 LCC의 경쟁력은 증가하게 됨을 알 수 있다. 따라서 고속철도의 티켓가격은 감소하고 FSC와 LCC의 티켓가격은 증가하게 된다. 또한 사회적 후생수준 고려 정도(θ)의 수준이 을 넘게 된다면, 오히려 Circular city model의 한계로 인하여 고속철도는 FSC와 경쟁하는 시장과 LCC와 경쟁하는 시장에서 모든 점유율을 가지고 오는 양상이 된다. 따라서 고속철도는 항공 교통수단간의 경쟁에서 모든 점유율을 확보하는 상태가 되어 고속철도 터미널의 접근시간(αH)이 증가함에도 불구하고 계속해서 티켓가격이 증가함을 알 수 있다.
Proposition 4.
고속철도 터미널의 접근시간(αH)이 증가할수록, FSC와 LCC의 점유율은 증가하고 고속철도의 점유율은 떨어진다.
이에 대한 증명과정은 다음과 같다.
Proof.
| $$\frac{\sigma x^\ast}{\sigma\alpha_H}=0$$ | (32) |
| $$\frac{\sigma y_{}^\ast}{\sigma\alpha_H}=\frac{6v}{(60-49\theta)}>0$$ | (33) |
| $$\frac{\sigma z_{}^\ast}{\sigma\alpha_H}=\frac{6v}{(60-49\theta)}>0$$ | (34) |
각 교통수단의 점유율을 도출해낼 수 있는 Equations 20-22를 고속철도 터미널의 접근시간(αH)로 1차 미분한 결과, 고속철도 터미널의 접근시간(αH)의 변화와 두 항공수단의 최적 점유율은 양의 관계를 가짐을 Equations 33, 34를 통해서 알 수 있다. Equation 32는 0의 값을 가지기에 고속철도 터미널의 접근시간(αH)의 변화와 고속철도의 최적 점유율은 관계가 없다고 생각 할 수 도 있지만, FSC와 LCC의 점유율이 상승하면 결과적으로는 고속철도의 점유율이 하락할 것 이다. 이를 통해 고속철도 터미널의 접근시간(αH)이 증가할수록 고속철도는 경쟁력이 떨어지게 되며 항공 교통수단과의 경쟁에서 점유율을 잃게 됨을 알 수 있다.
Proposition 5.
(ⅰ) 고속철도의 한계비용이 매우 작은 경우 세 교통수단의 티켓 가격 모두 고속철도의 속도(sH)가 증가할수록 감소하게 된다.
(ⅱ) 고속철도의 한계비용이 매우 큰 경우, 세 종류의 교통수단 모두 고속철도의 속도(sH)가 증가할수록 함께 티켓 가격이 증가하게 된다.
(ⅲ) 고속철도의 한계비용이 앞선 두 가지에 해당하지 않는 경우에는 고속철도의 속도(sH)가 증가할수록 고속철도의 티켓 가격만이 증가하고 나머지 두 종류의 교통수단인 FSC와 LCC의 티켓 가격은 감소한다.
이에 대한 증명과정은 다음과 같다.
Proof.
| $$\frac{\sigma p_H^\ast}{\sigma s_H}=\frac1{(60-49\theta)}(18\frac{\sigma C_H}{\sigma s_H}-7(7\theta-6)\frac{v\cdot l_H}{s^2H})$$ | (35) |
| $$\frac{\sigma p_F^\ast}{\sigma s_H}=\frac6{(60-49\theta)}(\frac{\sigma C_H}{\sigma s_H}-\frac{v\cdot l_H}{s^2H})$$ | (36) |
| $$\frac{\sigma p_L^\ast}{\sigma s_H}=\frac6{(60-49\theta)}(\frac{\sigma C_H}{\sigma s_H}-\frac{v\cdot l_H}{s^2H})$$ | (37) |
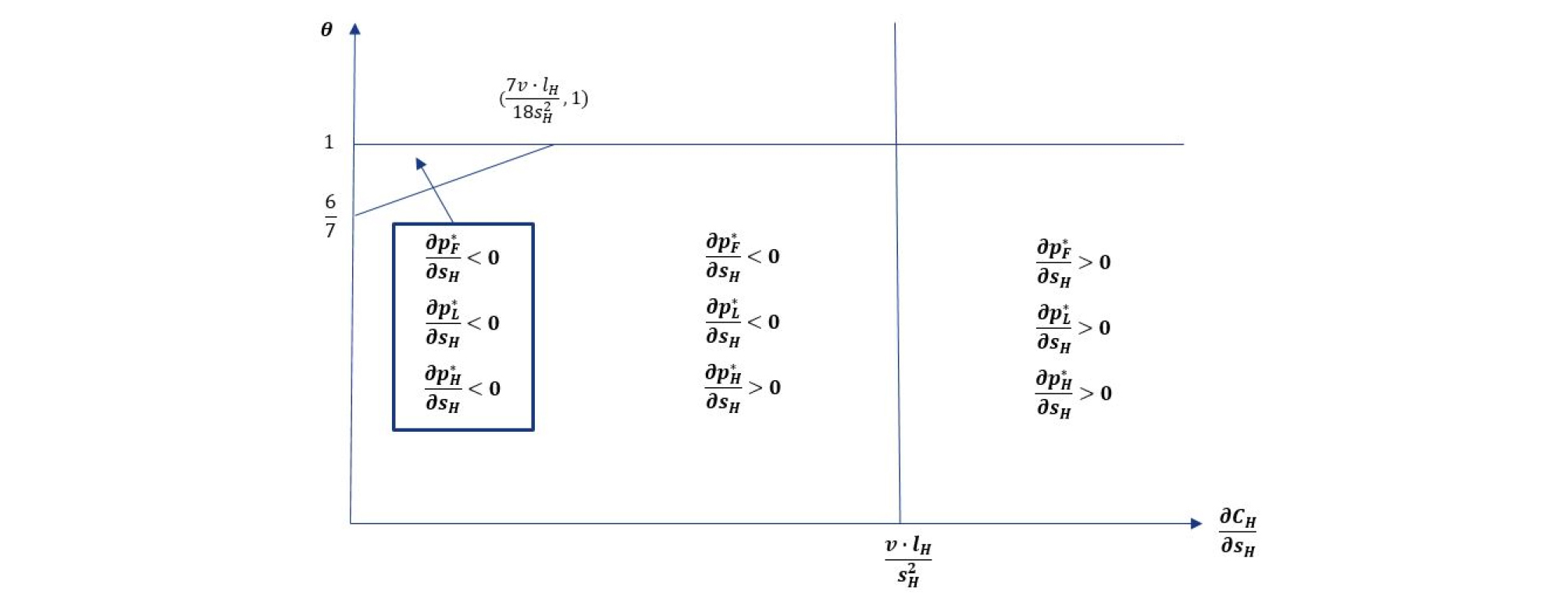
각 교통수단의 최적 가격을 나타내는 Equations 17-19를 고속철도의 속도(sH)로 1차 미분한 결과, 고속철도의 속도(sH)에 따른 각 교통수단의 티켓가격의 변화는 고속철도의 속도(sH)에 대한 고속철도의 한계비용 수준에 따라 달라짐을 알 수 있다. 이를 그래프로 나타내면 Figure 2와 같다. 고속철도의 한계비용 구분은 한계비용이 충분이 작은 왼쪽 상단구간, 한계비용이 충분히 큰 오른쪽 구간, 둘 다 해당 안 되는 중간부분 총 세 구간으로 나누어진다.
이를 통해 고속철도의 속도(sH)에 대한 한계비용의 수준이 작은 경우, 고속철도가 속도(sH)를 올림에 따라 각 교통수단 간의 경쟁은 심화되며, 그 결과 세 가지의 교통수단 모두 티켓가격이 감소할 것이라 판단할 수 있다. 반대로 고속철도의 한계비용이 커지는 경우, 고속철도는 고속철도의 속도(sH)을 낮출 것이며, 이에 따라 항공 교통수단의 경쟁력은 올라가고 FSC와 LCC의 티켓가격이 증가할 것이라 판단 할 수 있다. 반면 고속철도의 경우에는 높은 한계비용으로 인해 오히려 티켓가격이 증가하게 될 것이다.
Proposition 6.
(ⅰ) 고속철도의 한계비용이 매우 큰 경우, 고속철도의 속도(sH)가 증가할수록 고속철도의 점유율이 줄어든다.
(ⅱ) 고속철도의 한계비용이 크지 않은 경우에는 고속철도의 속도(sH)가 증가할수록 고속철도의 점유율이 증가하게 된다.
이에 대한 증명과정은 다음과 같다.
Proof.
| $$\frac{\sigma x_{}^\ast}{\sigma s_H}=0$$ | (38) |
| $$\frac{\sigma y_{}^\ast}{\sigma s_H}=\frac6{(60-49\theta)t}(\frac{\sigma C_H}{\sigma s_H}-\frac{v\cdot l_H}{s^2H})$$ | (39) |
| $$\frac{\sigma z_{}^\ast}{\sigma s_H}=\frac6{(60-49\theta)t}(\frac{\sigma C_H}{\sigma s_H}-\frac{v\cdot l_H}{s^2H})$$ | (40) |
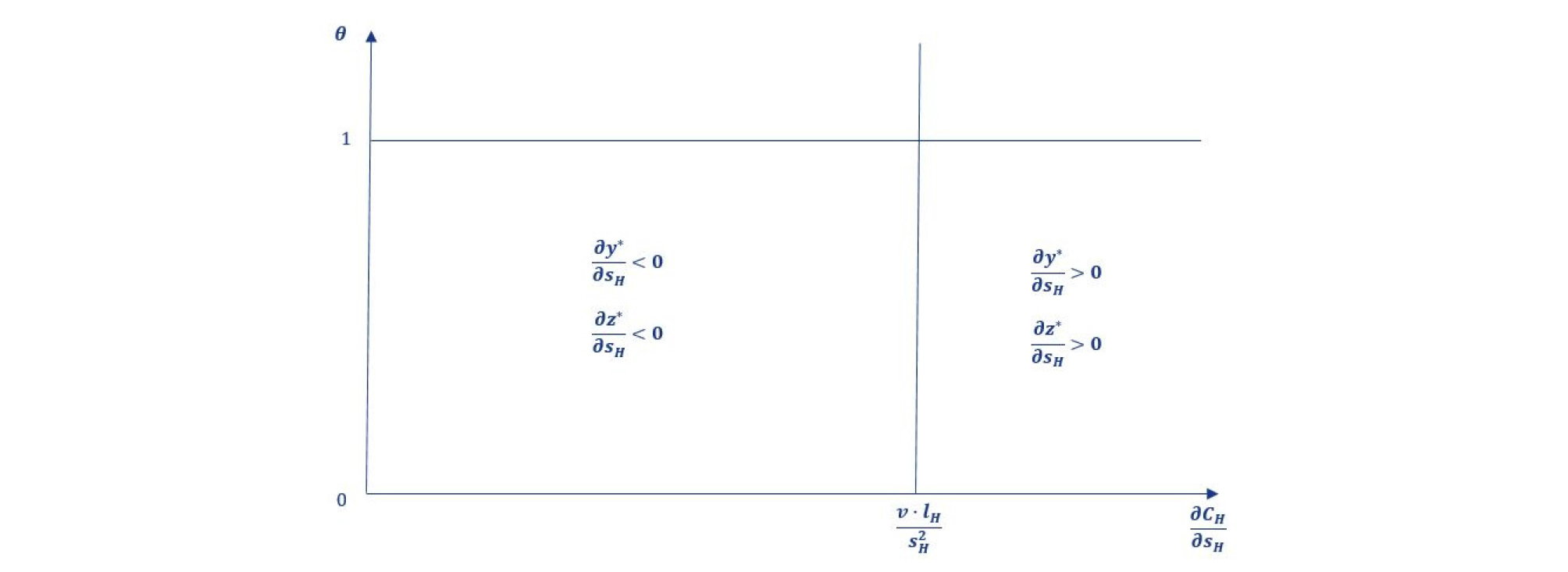
각 교통수단의 점유율을 도출해낼 수 있는 Equations 20-22를 고속철도의 속도(sH)로 1차 미분한 결과, 고속철도의 속도(sH)에 따른 각 교통수단의 점유율의 변화는 고속철도의 속도(sH)에 대한 고속철도의 한계비용 수준에 따라 달라짐을 알 수 있다. 이를 그래프로 나타내면 Figure 3과 같다. 고속철도의 한계비용 구분은 한계비용이 충분히 큰 오른쪽 구간, 한계비용이 크지 않은 왼쪽 구간 총 2가지 구간으로 나누어진다.
이를 통해 고속철도의 속도(sH)에 대한 고속철도의 한계비용이 커지는 경우에는 고속철도는 고속철도의 속도(sH)를 낮출 것이며, 이는 항공 교통수단의 경쟁력을 높이게 되어 FSC와 LCC의 점유율이 증가한다는 것을 알 수 있다. 이와 반대로, 고속철도의 속도(sH)에 대한 고속철도의 한계비용이 낮은 경우에는 고속철도는 고속철도의 속도(sH)을 높일 것이며, 이로 인해 고속철도의 경쟁력이 올라가기에 점유율 또한 증가하게 될 것이라는 것을 알 수 있다.
연구모형의 서울-부산 노선에 대한 적용
1. 서울-부산 노선의 실제 자료를 통한 모형 결과 추정
설정한 모형을 활용해 국내에서 가장 교통수요가 많은 서울-부산 노선에 대한 실제 데이터를 바탕으로 세 가지 교통수단의 최적 운임과 점유율을 도출하였다. 서울-부산 노선에 대한 최적 운임과 점유율을 통해 현재 서울-부산 노선의 상황을 분석하고, 서울-부산 노선의 각 교통수단의 실제 운임과 점유율과의 비교 분석을 통해 본 연구에서 최종적으로 추정된 모형의 유효성을 입증할 수 있으며, 서울-부산 노선의 운송시장 분석을 통해 다양한 시사점을 도출할 수 있다. 본 연구에 활용된 서울-부산 노선의 실제 자료는 Table 2와 같다.
Table 2. Actual data on the Seoul-Busan route used for the developed model
대부분의 자료는 코레일과 각 항공사의 공식사이트에서 자료를 입수하였으며, 시간 가치(v)의 경우, 국내 연간GDP를 총 근로시간으로 나누어 추정하였다. 운영시간(Ti)의 경우 각 교통수단의 첫 번째와 마지막 운행시간을 활용해 나타내었으며, 접근시간(αi)의 경우 평균적으로 공항보다는 철도 터미널로의 접근시간이 더 작음을 고려하여 일정 시간의 차이를 두어 가정하였다. 각 교통수단의 변동비용(Ci)의 경우, 자료를 구할 수 없었기에 항공 교통수단의 경우, 고속철도보다 변동비용이 더 높다고 가정하였으며, 항공 교통수단 간에서도 FSC가 LCC보다 높은 수준의 변동비용을 가진다고 가정하였다. 또한 총 소비자 효용(b)과 비효율 변수(t)에 대한 값도 실제 자료를 활용하기 어려움이 있었기에, 다른 값들을 활용하여 각 교통수단의 최적운임과 점유율에 대한 값을 여러 번 도출해보았으며 실제로 모든 결과에서 일정한 값을 보였기에 이와 같이 가정한 후 각 교통수단에 대한 최적운임과 점유율을 도출하는 과정을 수행하였다.
2. 서울-부산 노선의 실제 자료와 추정모형 값의 비교분석
5년간의 각 교통수단의 점유율과 운임은 각 교통수단의 공시자료를 사용하였으며, 티켓 가격의 경우에는 2011년부터 2015년까지 운임의 변동이 없었기에 동일한 운임으로 비교분석을 수행하였다. 추정 모형의 분석결과와 서울-부산 노선의 실제 데이터의 비교분석의 결과는 Tables 3, 4로 정리하였다.
Table 3. Optimal price and market share of Seoul-Busan route derived from the developed model
Table 4. Actual prices and share of Seoul-Busan routes from 2011 to 2015
이를 통해 세 가지 교통수단 모두가 사회적 후생수준 고려 정도(θ)의 수준이 0.05에 머무를 때 추정된 모형으로 도출한 최적가격과 실제가격이 근사함과 세 교통수단의 최적점유율과 실제 점유율의 양상이 근사함을 통하여 Circular city model을 활용하여 최종적으로 도출한 고속철도, FSC, LCC의 경쟁 모형이 유효함을 입증 할 수 있다.
반면 개발모형을 통해 추정한 점유율과 2011년부터 2015년까지의 서울-부산 노선의 실제 점유율을 비교하면 실제 점유율에서 고속철도가 개발모형을 통해 추정된 점유율에 비해 월등히 높음을 알 수 있다. 사회적 후생수준 고려 정도(θ)이 0.05수준이라는 것은 서울-부산 노선에서 고속철도는 공공성을 고려한 사회적 복지 수준이 매우 낮음을 의미한다. 이렇게 된다면 실제로는 항공사의 경쟁력이 높아지면서 점유율이 올라가야하지만 고속철도 시장이 거의 독점에 가까운 75%에서 80% 사이의 점유율을 가지고 있다. 이는 데이터 상에서도 그 차이를 볼 수 있듯이 운항횟수, 접근시간, 운영시간 세 부분에서의 차이가 서로 맞물려 소비자의 편의라는 측면에서 고속철도 시장에 긍정적인 영향을 미쳐 점유율을 높였다고 해석할 수 있다. 높은 점유율을 보이는 서울-부산 노선에 한해 고속철도는 사회적 후생수준 고려 정도(θ)를 낮추고 이 수익을 통해 공항을 이용하기 어려운 지역에서 사회적 후생수준 고려 정도(θ)의 수준을 높임으로써 국내 교통수단의 공공성을 높이고 있다고 판단된다.
시사점
본 연구에서는 각 교통수단의 목적을 최대화하기 위해 나아가야할 전략에 대해, 특정 변수를 활용하여 각자의 점유율을 높일 수 있는 방향을 제시하였다. 본 연구를 통해 고속철도, 항공 교통 수단, 정부의 입장에서 모형 분석결과에 대하여 시사하는 바를 알아보고자 한다.
고속철도의 입장에서 사회적 후생수준 고려 정도(θ)의 수준을 높일수록 다른 교통수단과의 경쟁에서 점유율을 높게 차지하지만 이에 따른 수익률 또한 낮아지기에 최적의 수준을 유지하는 전략이 필요하다. 고속철도의 속도(sH)는 높아질수록 총 여행 시간(jH)는 줄어들기에 고속철도의 경쟁력이 커지지만, 한계비용의 증가로 인해 티켓가격도 증가하여 오히려 점유율을 잃게 되는 상황이 벌어질 수 있음을 분석결과로 확인하였다. 따라서 고속철도의 속도(sH)를 통한 전략은 현재 한계비용 수준을 정확히 파악한 후에 계획해야 된다.
본 연구의 결과를 통해 고속철도의 사회적 후생수준 고려 정도(θ)가 항공교통수단의 운임과 점유율에 큰 영향을 주는 것을 알 수 있었다. 따라서 항공 교통수단은 고속철도와의 경쟁에서 경쟁우위를 얻기 위해 현재 고속철도의 사회적 후생수준 고려 정도(θ) 수준을 정확히 파악한 뒤, 그에 맞는 전략을 세워야 할 것이다. 또한, 총 여행시간(jF, jL)을 줄이기 위해 이와 관련된 변수인 공항의 접근시간(αF)을 줄이는 전략과 운항횟수(fF, fL), 항공 교통수단의 속도(sF, sL)를 증가시키는 등의 전략을 고려하여야만 한다.
정부는 사회적 복지를 위해 고속철도의 사회적 후생수준 고려 정도(θ) 수준을 조정할 수 있다. 하지만 사회적 후생수준 고려 정도(θ)의 수준을 너무 높게 측정하게 되면, 고속철도와 항공 교통 수단이 경쟁하는 시장에서 고속철도의 모든 점유율을 가지게 되는 독점상황이 생겨 버린다. 따라서 정부는 이러한 고속철도가 독점을 하는 상황을 미연에 방지하기 위해서 항상 사회적 후생수준 고려 정도(θ)의 수준을 정확히 통제하는 계획을 세워야 한다.
결론
고속철도의 진입으로 인해 가장 큰 영향을 받는 교통수단은 바로 항공 교통수단이다. 항공 교통수단은 고속철도의 속도가 증가함에 따라 중단거리 뿐만이 아니라 장거리 노선에서도 고속철도와 경쟁구도를 이루게 되었고, 이로 인해 전반적인 항공시장의 수요가 감소하였다. 고속철도와 항공사 간의 높은 점유율을 차지하기 위한 경쟁이 갈수록 치열해지기에, 고속철도와 항공사의 관계를 분석하는 연구의 중요성 또한 계속해서 높아지고 있는 상황이다.
본 연구에서는 Circular city model을 활용하여 고속철도와 FSC, LCC의 경쟁시장을 분석하고 경쟁력을 높이기 위한 최적의 운임과 그 경우의 점유율을 도출하는 모형을 개발하였다. 또한 개발한 최적 가격과 점유율에 대한 모형이 고속철도의 경쟁전략 요인인 사회적 후생수준 고려 정도(θ), 터미널 접근시간, 고속철도 속도에 의해 어떻게 변화하는지 분석함으로써 고속철도가 어떠한 요인을 관리하여야 하는 가를 구체적으로 제시하였다. 특히 국내에서 가장 높은 수요를 가진 노선인 서울-부산 노선에 개발모형을 적용함으로써 서울-부산 노선의 고속철도와 FSC, LCC의 최적가격과 점유율을 도출하고 분석하였다. 개발 모형을 통해 서울-부산 노선의 교통시장의 상황을 분석함으로써 모형의 유효성을 입증하는 동시에 국내 교통시장에서 고속철도와 항공사의 관계를 파악하였다. 본 연구는 향후 국내 교통수단의 발전을 위한 경쟁전략 수립에 많은 도움을 줄 수 있다고 본다.
본 연구는 기존 선행연구와는 다르게 항공사를 FSC와 LCC로 구분지어 고속철도와의 경쟁전략을 비교분석한다는 점에서 큰 차별성을 가졌으나, 모형상의 한계로 한 시장이 최대로 가질 수 있는 점유율이 로 제한되어 독점시장의 상황을 분석할 수 없다는 한계점을 가지고 있다. 이러한 모형상의 한계점을 보완한다면 교통시장을 보다 현실적으로 분석할 수 있을뿐더러, 서울-부산 노선 이외에도 다양한 노선에 이를 적용할 수 있다는 높은 범용성을 가졌다는 점에서 의의를 가진다. 본 연구가 국내뿐만 아니라 다양한 노선에서 고속철도와 항공사의 경쟁전략의 비교분석에 있어서 유용하고 자주 활용되어지기를 기대한다.