서론
문헌고찰
1. 사고 지속시간 정의
2. 사고 지속시간 선행연구
3. 선행연구와의 차별성
4. 이론적 고찰
사고 자료
1. 자료의 특성
2. 변수의 설정
모형의 추정 및 해석
1. 프레일티 모형 구축 및 평가
2. 모형의 해석
결론
서론
교통 혼잡은 교통수요가 도로의 용량을 초과하는 경우 발생하며, 반복적 발생 혼잡(recurrent congestion)과 비반복적 발생 혼잡(non-recurrent congestion)으로 구분된다. 반복적 발생 혼잡은 정해진 시공간에 대하여 규칙적으로 혹은 반복적으로 발생되는 혼잡을 말하며, 출퇴근 시간에 발생하는 혼잡이 대표적이다. 반면, 비반복적 발생 혼잡은 특정 도로 구간의 용량이 일시적으로 감소하거나 일시적으로 교통수요가 급증하여 발생하는 혼잡을 말하며, 주로 교통사고, 차량고장, 도로공사, 기상악화, 대규모 행사와 같은 돌발상황으로 인해 발생한다. 국내의 경우 돌발상황 중 교통사고가 차지하는 비율은 44% 수준에 이르는 것으로 조사되었다(Kim and Lee, 2015; Lee et al., 2015).
교통사고로 인한 비반복적 발생 혼잡을 감소시키기 위해 많이 노력들이 이루어지고 있다. 특히 교통사고는 발생 시간과 장소에 대한 예측이 어렵기 때문에, 돌발상황관리 시스템(incident management systems)과 같은 교통사고 발생한 이후 신속한 사고의 대응분야에 대한 연구가 활발히 진행되어왔다(Chung et al., 2010; Chung, 2017). 이 중 교통사고 관리 시스템(accident management system)의 주요 목적은 교통사고를 신속하게 처리하여 교통 혼잡을 최소화하는 것이다. 교통사고를 신속하게 처리하기 위해 운영자는 교통사고를 신속하게 파악(검지)하고 현장에 투입되는 인원과 장비를 적절하게 배치해야 한다. 즉, 신속한 교통사고 검지와 처리가 기본이며, 이렇게 사고의 검지와 처리 과정에 소요된 시간을 사고 지속시간(crash duration)이라 부른다.
결과적으로 교통사고로 인한 비반복적 발생 혼잡의 감소를 위해서는 사고 지속시간에 대한 이해가 필요하다. 또한, 사고 지속시간에 대한 이해는 사고 지속시간에 영향을 미치는 인자에 대한 파악이 기본이며, 이를 기반으로 제어 혹은 관리 가능한 인자의 구분 및 해석이 동반되어야 한다. 이러한 결과는 교통사고에 대한 처리 전략 수립은 물론 교통사고로 인한 비반복적 발생 혼잡의 감소 전략 수립에 활용된다. 이러한 배경으로 교통사고 지속시간에 대한 연구는 1980년대부터 전세계적으로 꾸준히 진행되어 왔다. 대부분의 연구는 회귀분석을 기반으로 진행되었으며, 일부 인공지능 기법이나 전문가 시스템을 기반으로 수행되었다. 회귀분석 기반 접근 방식의 경우, 사고 지속시간에 대한 분포는 좌우 대칭인 정규분포 보다는 로그 정규분포(log-normal distribution)와 같이 양의 왜도값(positive skewness)을 가진 분포를 형성하는 경우가 일반적이다. 따라서 생존분석(survival analysis) 혹은 지속시간 모형(duration model)을 주로 적용해 왔다. 특히, 모수적(parametric) 생존분석 모형을 적용한 대부분의 연구는 비관측 이질성(unobserved heterogeneity)을 모형에 고려하지 않았다. 즉, 공변량(covariate) 값이 동일한 개별 교통사고 지속시간의 분포는 동일할 것이라는 가정하에 모형을 구축한 것이다. 그러나 지속시간에 영향을 미칠 수 있는 모든 공변량이 모형에 포함된 것은 아닐 수 있다. 즉, 비관측 이질성이 존재할 수 있다는 것이다.
본 연구의 목적은 기존 연구들과 다르게 비관측 이질성을 고려하여 고속도로 교통사고 지속시간에 영향을 미치는 인자를 파악하는 것이다. 이를 위해 2018년 전국 고속도로에서 발생한 7,646건의 교통사고 자료를 기반으로 비관측 이질성을 고려한 프레일티(frailty) 모형을 구축하였다.
문헌고찰
1. 사고 지속시간 정의
사고 지속시간에 대한 정의는 다음과 같이 4단계로 정의할 수 있다(TRB, 1994; Nam and Mannering, 2000; Chung et al., 2007; Chung, 2010; Chung et al., 2010; Chung and Kim, 2017). (1)사고 검지 및 제보시간(사고가 발생한 후 검지 및 제보 될 때까지의 소요시간), (2)대응시간(사고가 접수된 후 사고 처리 팀이 현장에 도착할 때까지의 소요시간), (3)처리시간(사고 처리 팀이 현장에 도착한 후 처리를 완료할 때까지의 소요시간), (4)회복시간(사고 처리가 완료된 후 정상 교통류로 회복될 때까지의 소요시간). 본 연구에서 사고 검지 및 제보시간, 대응시간, 처리시간까지 3단계를 사고 지속시간으로 정의하였다. 즉, 사고 지속시간은 사고 검지 및 제보시간, 대응시간, 처리시간에 따라 결정된다.
2. 사고 지속시간 선행연구
국외의 경우, Golob et al.(1987)은 캘리포니아 고속도로에서 트럭이 포함된 사고를 분석하였고, 사고 지속시간은 로그-정규 분포를 따른다는 것을 연구하였다. Khattak et al.(1995)은 Time sequential procedure 방법을 활용하여 시카고 고속도로 사고 지속시간을 분석하였다. Smith and Smith(2002)는 비모수 회귀 모형, 의사결정나무를 활용하여 버지니아 고속도로 사고 처리시간을 분석하였다. Ozbay and Noyan(2006)은 베이지안 네트워크(Bayesian Networks) 방법을 활용하여 버지니아 사고 처리시간을 분석하였다.
Jones et al.(1991)은 시애틀 고속도로에서 사고 지속시간을 생존분석을 활용하여 분석하였고, 이후 사고 지속시간에 대한 연구에서 생존분석이 많이 활용되었다. Nam and Mannering(2000)은 생존분석을 활용하여 워싱턴 고속도로 사고를 분석하였다. 사고 검지 및 제보시간(와이블 분포), 대응시간(와이블 분포), 처리시간(로그-로지스틱 분포) 각 시간별로 모형을 정립하였다. Chung(2010)은 생존분석을 활용하여 한국 고속도로 사고 지속시간을 분석하였다. 시간이 지남에 따라 사고 지속시간 패턴이 변하기 때문에 시간적 이전 가능성(temporal transferability)을 평가하였다. Al Kaabi et al.(2011)은 생존분석을 활용하여 아부다비 도시의 사고 처리시간을 분석하였다. AIC(Akaike Information Criterion) 테스트를 통해 와이블 분포를 선택하였다. Al Kaabi et al.(2012)은 생존분석을 활용하여 아부다비 고속도로의 사고 대응시간을 분석하였고, 비관측 이질성을 고려하였다. Hojati et al.(2013)은 생존분석을 활용하여 퀸스랜드 고속도로 사고 지속시간을 분석하였다. 충돌(Crash), 위험물(Hazard), 정차 차량(Stationary vehicle)으로 분류하여 모형을 정립하였고, 임의의 파라미터(random parameter)와 고정 파라미터(fixed parameter)를 사용하였다.
국외뿐만 아니라, 국내에서도 지속시간에 대한 다양한 연구가 이루어졌다. Shin and Kim(2002)은 다중회귀분석을 활용하여 주야간, 사상자 유무, 통합모형으로 분류하여 고속도로 돌발상황 지속시간을 분석하였다. Shin(2004)은 의사결정나무 방법을 활용하여 고속도로 돌발상황 지속시간을 분석하였다. Chung et al.(2007)은 생존분석을 활용하여 고속도로 사고 지속시간에 대해 분석하였다. Lee et al.(2015)은 의사결정나무와 K-Nearset Neighbor(KNN)모형을 융합한 hybrid 모형을 활용하여 고속도로 사고 처리시간을 분석하였다. Chung and Kim(2017)은 Cox 모형을 활용하여 고속도로 사고 처리시간에 영향을 주는 인자를 분석하였다.
3. 선행연구와의 차별성
결과적으로 사고 지속시간에 관련된 연구에서는 생존분석을 주로 적용해 왔으며, 대부분의 선행 연구는 비관측 이질성을 무시하고 모형을 구축해왔다. 그러나 생존분석을 활용하여 사고 지속시간을 연구할 때, 비관측 이질성이라 불리는 중요한 변수를 생략하게 되면, 편향된(biased) 추정으로 이어질 수 있다(Hensher and Mannering, 1994; Chung et al., 2015; Washington et al., 2020). 이러한 한계점을 극복하기 위해, 비관측 이질성을 고려한 사고 지속시간 연구가 진행되었다(Al Kaabi et al., 2012; Chung et al., 2015; Liu et al., 2020). 국내에서도 사고 지속시간에 대한 연구는 꾸준히 진행되고 있지만, 비관측 이질성을 고려한 연구는 전무한 것으로 조사되었다. 이를 통해 본 연구에서는 생존분석 기법 중 비관측 이질성을 고려할 수 있는 프레일티 모형을 활용하여 교통사고 지속시간에 영향을 미치는 요인을 분석하고자 한다.
4. 이론적 고찰
프레일티는 관측되지 않는 변수 때문에 가지는 이질성을 다룰 수 있는 접근법이다. 프레일티 용어는 Vaupel et al.(1979)에 의해 처음 도입되었으며, 프레일티 모형은 음이 아닌 프레일티 파라미터 를 위험 함수에 추가함으로써 다음과 같은 조건부 프레일티가 된다.
는 음이 아닌 임의의 변수 t를 가지는 위험 함수를 나타낸다. 그리고 는 프레일티를 포함함으로써 수정된 위험 함수를 의미한다. 만약, >1 일 경우, 해당 위험 수준은 평균 보다 커진다. 반면, <1 일 경우, 해당 위험 수준은 평균 사고 보다 작아지며 덜 “연약(frail)” 함을 나타낸다.
위험 함수와 생존 함수의 관계로부터, 프레일티를 조건으로 하는 생존 함수는 와 같이 나타낼 수 있으며, 은 로그-정규(log-normal), 로그-로지스틱(log-logistic), 와이블(Weibull), 곰페르츠(gompertz) 분포와 같은 표준 모수적 모형의 생존 함수이며, 는 프레일티를 나타낸다. 또한, 관측되지 않는 를 적분함으로써 모집단 생존 함수를 얻을 수 있다. 만약 가 확률 밀도 함수 를 가질 경우, 비조건부 생존 함수는 다음과 같다.
수학적으로 다루기 쉽기 때문에, 는 감마 분포와 역-가우시안(inverse-Gaussian) 분포가 주로 사용된다. 만일, 가 감마 분포를 따를 경우, 평균 1, 편차 를 가진다.
그리고 비조건부 생존 함수는 다음과 같다.
가 역-가우시안 분포를 따를 경우 다음과 같으며,
이에 따른 비조건부 생존 함수는 다음과 같다.
사고 자료
1. 자료의 특성
본 연구는 2018년 1월부터 12월까지 전국 고속도로에서 발생한 총 8,636건의 교통사고 자료를 활용하였다. 고속도로에서 발생하는 교통사고들은 한국도로공사에서 관리하고 있으며, 자체적인 양식에 따라 입력된 자료이다. 입력된 자료는 (1)사고시간, (2)시간적 특성(계절, 시간), (3)사고 특성(사고 위치, 사고 유형, 차량 유형, 차량 피해, 사고후 차량 위치, 사고후 차량 상태, 사고 심각도, 사고차량수), (4)환경적 특성(작업 구간, 기상 상태, 조명시설), (5)운영적 특성(사고제보 유형)으로 구분하여 분석에 활용하였다. 총 8,636건의 자료가 수집되었으나, 사고 자료의 일부 속성 정보가 누락되었거나 혹은 정보가 부정확한 경우 연구에서 제외하였다1). 결과적으로 총 7,646건의 교통사고 자료만을 연구에 활용하였다.
1) “정보가 부정확한 경우”는 사고의 속성 정보 항목이 서로 일치하지 않는 경우를 의미함(예, 사고 관련 차량이 ‘화물차’로 분류되었지만, 관련 사고에 대한 기술자료는 ‘승용차’ 관련 사고로 기술된 경우).
2. 변수의 설정
변수는 자료의 형태에 따라 정량적 변수(quantitative variable)와 정성적 변수(qualitative variable)로 구분하였다. 정량적 변수로 사고차량수를 적용하였고, 나머지 정성적 변수들은 모두 더미변수(dummy variable)를 이용하여 분석에 적용하였다. 본 연구에서는 사고 지속시간을 종속변수로 사용하였으며, Table 1은 한국도로공사에서 관리하는 교통사고 자료를 기반으로 구축한 후보 변수들을 정리한 것이다. 이 표에서 계절에 대한 변수는 Chung et al.(2010), Chung(2010)에서 구분한 것과 같이 겨울(11월 29일-03월08일), 봄(03월09일-06월02일), 여름(06월03일-09월18일), 가을(09월19일-11월28일)로 정의하였다. 시간에 대한 구분은 오전첨두(07:01-09:00), 주간(09:01-17:00), 오후첨두(17:01-20:00), 야간(20:00-07:00) 4가지 시간대로 구분하였다. 사고 심각도에 대한 변수는 사망(사망 1명 이상 발생), 중상(중상 1명 이상 발생), 경상(경상 1명 이상 발생), 대물피해로 구분하였다. 나머지 변수들은 한국도로공사에서 입력한 자료를 기반으로 구분하였으며, 관련항목에서 자료의 수가 충분하지 않을 경우 유사한 항목 혹은 기타 항목에 포함하여 정의하였다.
Table 1.
Candidate variables
| Category | Variable | Crashes | Type | |
|
Temporal characteristics | Season | Winter | 1,481 | Dummy |
| Spring | 1,980 | Dummy | ||
| Summer | 2,141 | Dummy | ||
| Fall | 2,044 | Dummy | ||
| Time of day | AM peak | 819 | Dummy | |
| Midday | 3,323 | Dummy | ||
| AP peak | 967 | Dummy | ||
| Night | 2,537 | Dummy | ||
|
Crash characteristics | Location | Main lane | 5,111 | Dummy |
| Tunnel | 315 | Dummy | ||
| Ramp | 1,189 | Dummy | ||
| Tollgate | 883 | Dummy | ||
| Others* | 148 | Dummy | ||
| Crash type | Vehicle-facility | 4,408 | Dummy | |
| Vehicle-person | 37 | Dummy | ||
| Vehicle alone | 1,152 | Dummy | ||
| Rear-end | 1,421 | Dummy | ||
| Collision | 146 | Dummy | ||
| Others | 482 | Dummy | ||
| Vehicle type | Sedan | 3,906 | Dummy | |
| SUV | 877 | Dummy | ||
| Van | 311 | Dummy | ||
| Bus | 80 | Dummy | ||
| Small truck | 476 | Dummy | ||
| Midsize truck | 1,153 | Dummy | ||
| Large truck | 376 | Dummy | ||
| Truck with trailer | 390 | Dummy | ||
| Specially equipped vehicle | 77 | Dummy | ||
| Vehicle damage | Complete damage | 272 | Dummy | |
| Severe damage | 900 | Dummy | ||
| Minor damage | 2,904 | Dummy | ||
| Slight damage | 3,570 | Dummy | ||
|
Crash characteristics | Vehicle location after crash | Main lane | 3,859 | Dummy |
| Median | 113 | Dummy | ||
| Shoulder | 2,916 | Dummy | ||
| Off-road | 40 | Dummy | ||
| Opposite direction | 13 | Dummy | ||
| Other locations | 705 | Dummy | ||
| Vehicle status after crash | Stop | 6,913 | Dummy | |
| Rollover | 365 | Dummy | ||
| Overturn | 167 | Dummy | ||
| Fire | 201 | Dummy | ||
| Injury severity | Fatality | 178 | Dummy | |
| Severe injury | 85 | Dummy | ||
| Minor injury | 459 | Dummy | ||
| Property damage only | 6,869 | Dummy | ||
| Number of vehicles involved | 7,646 | Number | ||
|
Environmental characteristics | Work zone | Work zone | 98 | Dummy |
| No work zone | 7,548 | Dummy | ||
| Weather | Sunny | 4,872 | Dummy | |
| Cloudy | 689 | Dummy | ||
| Rainy | 1,793 | Dummy | ||
| Snowy | 272 | Dummy | ||
| Foggy | 20 | Dummy | ||
| Street lighting facility | No applicable (midday) | 3,513 | Dummy | |
| No street lighting | 848 | Dummy | ||
| Street lighting | 3,285 | Dummy | ||
|
Operational characteristics | Reporter type | CCTV | 255 | Dummy |
| Customer | 851 | Dummy | ||
| Traffic center | 778 | Dummy | ||
| Freeway service patrol | 2,646 | Dummy | ||
| Freeway information service provider | 644 | Dummy | ||
| Related agency | 1,761 | Dummy | ||
| Call center | 386 | Dummy | ||
| Others | 325 | Dummy | ||
모형의 추정 및 해석
1. 프레일티 모형 구축 및 평가
모수적 기법을 적용함에 있어서 위험 함수에 대한 적합한 분포를 선정해야 한다. 주로 사용되는 분포는 지수(exponential), 와이블(Weibull), 곰페르츠(Gompertz), 로그-정규(log-normal), 로그-로지스틱(log-logistic) 등이 있으며, 가장 적합한 분포를 선정하기 위해 AIC(Akaike’s Information Criterion) 방법이 활용된다(Chung et al., 2007; Chung et al., 2010; Al kaabi et al., 2011; Al Kaabi et al., 2012). AIC 방법은 Akaike(1974)에 의해 제시되었으며, AIC 값이 낮을수록 우수한 모형으로 평가된다. AIC는 Equation 7을 통해 구할 수 있다.
여기서, log-likelihood는 모형의 적합도를 나타내는 척도이며, k는 모형에서 상수항을 포함한 변수의 수를 나타낸다. 본 연구에서는 AIC 값 기반 최종적으로 와이블 분포를 선정하였다.
또한, 비관측 이질성에 대한 영향력을 평가하기 위해 감마(gamma)와 역-가우시안(inverse-Gaussian) 프레일티 분포를 적용하였다. 그 결과, 이전 연구와 마찬가지로(Chung, 2011; Chung and Recker, 2015) 감마 프레일티 와이블 모형이 최종적으로 선정되었으며, Table 2는 추정된 감마 프레일티 와이블 모형을 나타낸다. 이 모형에서 감마 프레일티 파라미터 는 0.367으로 추정되었으며, 이 값은 통계적으로 유의한 것으로 나타났다. 결과적으로 추정된 모형에서 비관측 이질성에 대한 효과는 유의한 것으로 평가되었다.
Table 2.
Weibull model with gamma frailty on estimated crash duration
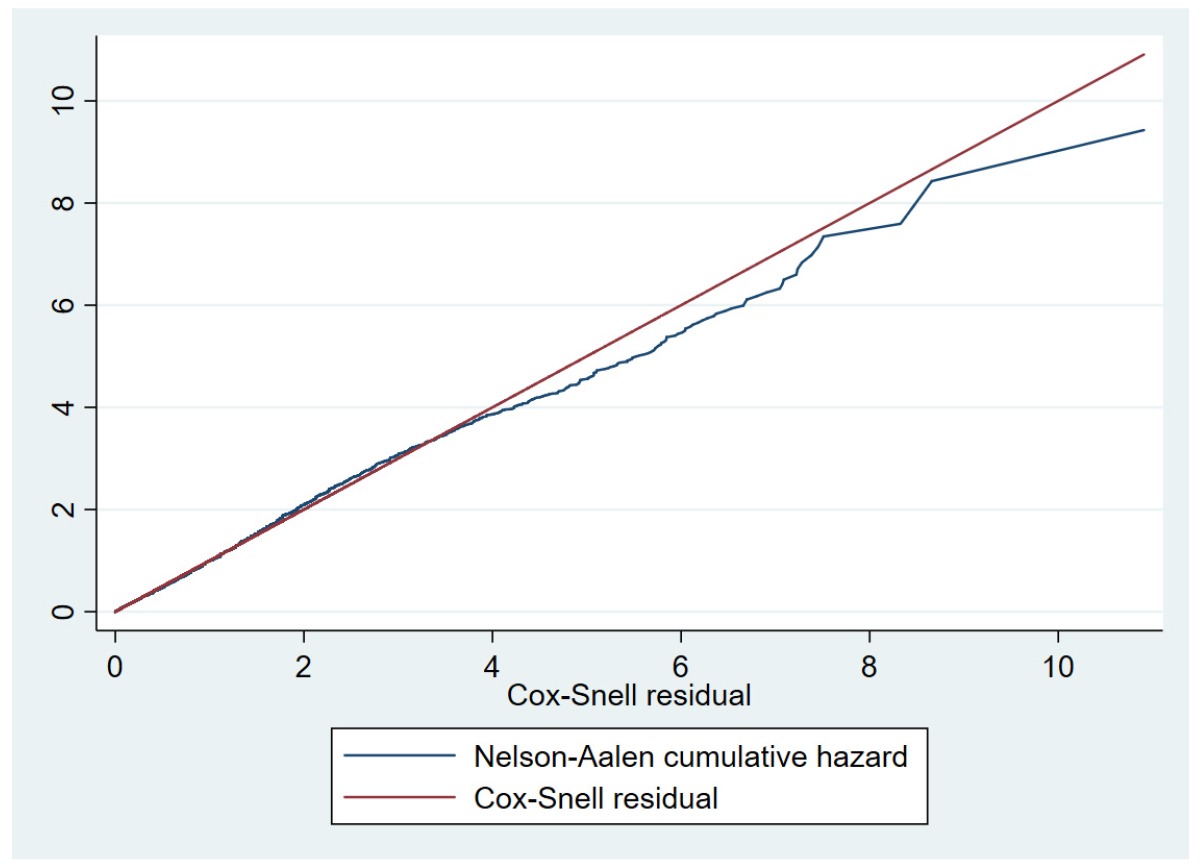
한편, 비관측 이질성을 고려하지 않은 와이블 기반 모형의 AIC 값은 16,346.53이며, 비관측 이질성을 고려한 감마 프레일티 와이블 모형의 AIC 값은 15,876.39으로 나타났다. 즉, 비관측 이질성을 고려한 모형이 비관측 이질성을 고려하지 않은 모형에 비해 AIC 값이 우수한 것으로 나타났다. 마지막으로, 추정된 모형에 대한 적합성 평가를 위해 콕스-스넬 잔차(Cox-Snell residuals)를 활용하였다. 즉, 콕스-스넬 잔차에 대한 누적 위험 추정치가 원점을 지나며 기울기가 1인 그래프가 형성된 경우 추정된 모형은 적합한 것으로 평가한다(Cleves et al., 2008). Figure 1에 제시된 것처럼, 콕스-스넬 잔차에 대한 누적 위험 추정치 그래프는 비교적 기울기가 1인 그래프 방향으로 형성되었기 때문에, 사고 지속시간에 대한 모형이 적합하다고 평가할 수 있다.
2. 모형의 해석
Table 2는 프레일티 모형으로 교통사고 지속시간을 추정한 결과를 요약한 것이며, 각 변수들은 유의수준 5%에서 유의한 것으로 나타났다. 모형에서 추정된 각 변수의 계수 값은 지수함수를 취함으로써 시간 비율(time ratio)로 해석하는 것이 일반적이다. Table 3은 각 변수에 대한 시간 비율 값을 제시한 것이다. 추정된 계수 값이 양이거나 시간 비율이 1보다 큰 경우 사고 지속시간은 증가하고, 계수 값이 음이거나 시간 비율이 1보다 작은 경우 사고 지속시간은 감소하는 것으로 해석한다.
Table 3.
Estimated time ratio and percentage changes
사고 특성 변수들 중 톨게이트에서 발생한 사고의 경우, 추정 계수값은 -0.113이다. 이 값에 지수함수를 취하면 exp(-0.113)=0.893가 되며, 톨게이트에서 발생한 교통사고는 다른 장소에서 발생한 교통사고에 비해 지속시간은 10.7% 감소하는 것으로 해석한다. 즉, 이러한 결과는 톨게이트 주변에서 사고가 발생할 경우, 견인차, 앰뷸런스 등과 같은 응급차량과 사고처리 팀의 접근성이 용이하여 지속시간이 감소한 것으로 추정된다. 다른 변수들도 동일한 방식으로 해석할 수 있다. 이를 토대로, 터널에서 발생한 교통사고는 다른 장소에서 발생한 교통사고에 비해 지속시간이 14.8% 증가하는 것으로 나타났다. 터널의 경우 장소의 특성상 밀폐되어 있어, 사고 처리 차량의 이동이 원활하지 못하여 작업시간이 길어져 사고 지속시간이 증가하는 것으로 볼 수 있다. 이전 연구 결과(Chung et al., 2007; Chung, 2010)와 같이 트레일러와 특수차량은 다른 유형의 차량 사고에 비해 사고 지속시간이 각각 36.1%, 33.8% 증가하는 것으로 나타났다. 트레일러와 특수차량의 경우 일반 차량에 비해 차량이 크기 때문에, 이를 견인하기 위해 대형견인차량이 필요하게 되어 사고 지속시간이 증가하는 것으로 볼 수 있다. 차량이 완파된 사고는 다른 유형의 차량 피해 사고에 비해 사고 지속시간이 23.5% 증가하는 것으로 나타났으며, 도로이탈 추락이 발생한 사고는 다른 유형의 차량 위치에 비해 사고 지속시간이 44.6% 증가하는 것으로 나타났다. 사고 후 차량의 상태가 전도 혹은 화재가 발생한 교통사고는 다른 유형에 비해 사고 지속시간이 44% 이상 증가하는 것으로 나타났다. 차량이 완파된 사고, 도로이탈 추락이 발생한 사고, 사고 후 전도 혹은 화재가 발생할 경우, 사고차량에 대한 견인 및 별도의 조치와 화재진압이 필요하여 사고 지속시간이 증가하는 것으로 볼 수 있다. 대물피해가 발생할 경우 사망자 혹은 부상자가 발생한 교통사고에 비해 사고 지속시간이 17.3% 감소하는 것으로 나타났다. 대물피해가 발생한 사고의 경우, 사고차량에 대한 처리만 이루어지고 인명 구조에 추가적인 조치가 필요하지 않기 때문에 사고 지속시간이 감소하는 것으로 볼 수 있다.
환경적 특성 변수들 중 조명이 없는 사고는 조명이 있거나 주간에 발생한 교통사고에 비해 사고 지속시간이 15.1% 증가하는 것으로 나타났다. 조명이 없을 경우 사고를 처리하는 과정에서 제한적인 시야 확보로 인해 사고 지속시간이 증가하는 것으로 볼 수 있다. 마지막으로, 운영적 특성 변수들 중 고속도로 순찰대의 순찰중 제보된 사고의 경우 다른 사고 제보 유형에 비해 사고 지속시간이 18.4% 감소하는 것으로 나타났으며, 이는 순찰대의 즉각적인 교통사고 현장의 정리 및 제어의 결과로 추정된다.
결론
본 논문은 고속도로에서 발생한 교통사고 지속시간에 영향을 미치는 요인을 분석하기 위해 프레일티 모형을 적용하였다. 그 결과 감마 프레일티 와이블 모형(Weibull model with gamma frailty)을 기반으로 사고 지속시간에 대한 모형이 추정되었으며, 총 11개의 변수가 사고 지속시간에 영향을 미치는 것으로 나타났다. 이중, 터널에서 발생한 사고, 트레일러 혹은 특수차량의 사고, 차량이 완파된 사고, 도로이탈 추락이 발생한 사고, 사고 후 전도 혹은 화재가 발생한 사고, 조명이 없는 곳에서 발생한 사고는 사고 지속시간을 증가시키는 요인으로 나타났다. 반면, 톨게이트에서 발생한 사고, 대물피해가 발생한 사고, 고속도로 순찰대의 순찰중 제보된 사고는 사고 지속시간을 감소시키는 요인으로 나타났다.
본 연구는 기존 연구와 달리 관측되지 않았지만 모형에 영향을 줄 수 있는 랜덤 효과(random effect)를 고려하기 위한 프레일티 모형을 적용하였다. 이 모형은 랜덤 효과를 고려하지 않은 일반 모형보다 설명력이 우수한 것으로 나타났으며, 그 결과 한국도로공사에서는 기존 연구 결과를 보완하여 사고 지속시간을 감소시키기 위한 전략의 수립도 가능할 것으로 판단한다. 한편, 본 연구는 1년간 전국 고속도로에서 발생한 교통사고 자료를 기반으로 수행되었다. 비록 8천여 건에 이르는 대규모 교통사고 자료를 기반으로 모형을 구축하였으나, 일부 변수에는 충분하지 못한 사고 자료를 포함하기도 하였다. 이러한 한계로 인해 다양한 변수들 간의 상호작용(interaction) 효과에 대한 분석은 진행하지 못했다. 그러나 다년간의 사고 자료를 확보하여 변수들 간의 상호작용 효과에 대한 분석을 통해 흥미로운 결과를 도출할 수 있을 것으로 판단된다. 또한, 사고 지속시간은 사고의 검지, 사고 현장에의 출동 및 처리 시간에 직접적인 영향을 받으며, 이러한 영향은 교통혼잡이나 도로의 기하구조, 지역에 따라 다르게 형성될 수 있기 때문에, 본 연구에서 고려하지 못한 이러한 인자들을 별도로 혹은 동시에 고려한 연구도 필요할 것으로 판단된다.