서론
1. 연구의 배경 및 목적
2. 연구의 대상과 범위
3. 연구수행 방법
선행연구
1. 항공 수요예측 관련 연구
2. 의사결정나무를 활용한 예측 관련 연구
3. 기존연구와의 차별성
이론적 고찰
1. 의사결정나무 소개
2. 의사결정나무 분석방법
3. CHAID 방법론
모형추정
1. 변수선정
2. 모형추정
모형검증
시사점
결론 및 향후과제
서론
1. 연구의 배경 및 목적
지난 1978년 ‘Airline Deregulation Act’가 미 의회에서 통과된 이후 시작된 항공시장 내 규제완화 움직임은 항공자유화를 거쳐 적극적인 항공노선 개방 등으로 확대되어왔다. 1995년 출범된 WTO 체제는 국가 간 관세 및 비관세 장벽이 급격히 낮췄으며, 다자무역체제 강화를 통한 무역장벽 완화는 국가 간 교역을 크게 확대시켰다. 글로벌 경제 성장과 교역환경 변화에 따른 국제 교역량 증가는 국제교역의 주요 운송수단인 항공운송에 대한 폭발적인 수요 증가와 더불어 항공운송산업의 지속적인 성장을 이끌었다. 지속적인 성장에도 불구하고 항공운송산업은 다양한 외부 환경변화 및 요인들에 의한 불확실성을 내포하고 있다. 이는 항공운송 수요가 갖고 있는 중간재적 성격과 파생수요라는 한계에 기인한다. 실제로 2001년 9.11테러, 2003년 SARS 확산, 2008년 글로벌 금융위기와 신종플루 유행, 2015년 MERS 발병, 2019년 미중무역 갈등 등 다양한 외부요소에 의해 항공운송시장이 영향을 받아왔다. 이외에도 경기침체, 환율변동, 유가변동 등으로 인해 항공운송시장이 직격탄을 맞는 경우를 어렵지 않게 목격할 수 있다. 이와 같은 항공운송산업의 불확실성은 항공운송시장 내 다양한 경제주체들의 생존전략에 큰 위험요소로 작용되어 왔다.
글로벌 항공운송시장은 저비용항공사의 성장과 시장 확대, 항공사 간 M&A 증가, 얼라이언스(Alliance)로 대표되는 항공사 간 전략적 제휴의 강화 및 확대 등 항공사 간 경쟁이 갈수록 심화되고 있다. 기존 항공사들은 경쟁에서 살아남기 위해 과거와 같은 몸집 키우기 식의 양적성장이 아닌 원가절감, 사업모델 다각화, 서비스 개선 등 질적 성장을 통한 경쟁력 강화를 모색하고 있다. 궁극적으로 보유자원의 활용률 극대화를 통한 운영효율성 증대와 지속성장을 위한 안정적인 성장 동력 확보가 항공사의 생존의 핵심 요소로 대두되고 있는 상황이다. 이러한 항공운송시장 내 환경변화는 공항 간 경쟁 역시 가속화되기 시작했다. 항공사의 허브앤스포크 네트워크(Hub & Spoke Network) 노선 형태에 따라 주요 공항 간의 허브경쟁이 심화되었고, 저가항공사의 확대와 다양한 노선에 대한 수요 확대는 중소규모 공항 간의 경쟁을 더욱 심화시키고 있다. 이러한 경쟁에서 살아남기 위해 개별 공항들은 효율성과 수익성 확보에 더욱 박차를 가하고 있다. 주요 공항들은 허브경쟁력을 잃지 않기 위해 공항시설을 지속적으로 확충하고 있으며 허브공항의 핵심요소인 네트워크 확대를 위해 노력하고 있다. 이와 더불어 운영 효율성 제고를 통한 수익성 확보에 집중하고 있다.
항공운송산업을 포함한 다양한 산업에서 운영 효율화 달성을 위한 가장 핵심적인 분야 가운데 하나가 바로 수요예측이다. 정확한 수요예측은 자원의 낭비를 최소화함으로써 한정된 자원의 활용도를 극대화 할 수 있다. 특히나 대규모 투자가 수반되며 항공기의 적재 공간은 재고가 없다는 특성으로 인해 수요 예측결과와 실제 수요 간의 발생하는 차이가 커질수록 자원의 낭비와 기회비용의 증가는 기하급수적으로 증가한다. 뿐만 아니라 항공수요예측은 정부, 공항, 항공사 등 항공 산업 내 다양한 경제주체들에게 의사결정에 기초자료 및 참고자료로 활용된다. 부정확한 예측은 항공 산업 내 모든 경제주체들의 비효율성을 증가시키는 결과를 야기한다. 그렇기 때문에 항공운송산업 내에서 수요예측에 대한 중요성은 그 어느 분야에서보다 강조되고 있으며, 항공운송산업 및 시장에서 실질적으로 적용 및 활용할 수 있는 정확한 수요 예측모형에 대한 다양한 연구가 활발히 진행되고 있다.
본 연구에서는 항공운송산업 내 다양한 분야에서 활용할 수 있는 정확한 수요예측 방법론을 개발하고 제안하고자 한다. 또한 예측단위를 년, 분기, 월 단위 같이 장기적이고 거시적인 운영계획에 활용하기 위한 예측모형이 아닌 일단위 예측이 가능한 모형을 개발함으로서 항공사 혹은 공항들의 세부 운영계획에 실질적인 도움을 줄 수 있는 방안을 제안하고자 한다. 이를 통해 항공사, 공항 등 다양한 서비스 공급 주체들의 운영효율성 및 수익성 향상과 더불어 향후 항공운송서비스 사용자들에게 더 높은 수준의 서비스가 제공될 것으로 기대된다.
2. 연구의 대상과 범위
본 연구에서 일단위 항공화물 수요예측 모형개발에 활용한 자료는 인천국제공항에서 출발한 K항공사의 일단위 항공화물 수출 물동량이다. K항공사의 일단위 수출 물동량 자료는 항공정보포탈 시스템 내 항공통계에서 제공 중인 노선별 수송현황 실시간 통계자료 가운데 K항공사의 자료만을 따로 추출하여 활용하였다.1) 본 연구에서 활용한 자료의 구체적인 기간은 2010년 1월 3일부터 2018년 12월 22일까지이다. 이 가운데 예측모형 개발과정에서 training set으로 활용한 자료는 2010년 1월 3일부터 2018년 10월 26일까지의 자료이며, 예측정확도 검증을 위한 test set으로 활용한 자료는 2018년 10월 27일부터 2018년 12월 22일까지의 자료이다.2) 이외에 본 연구에서 사용한 자료 중 공휴일 변수는 실제 해당기간에 있었던 국내 공휴일 정보를 사용하였다.
3. 연구수행 방법
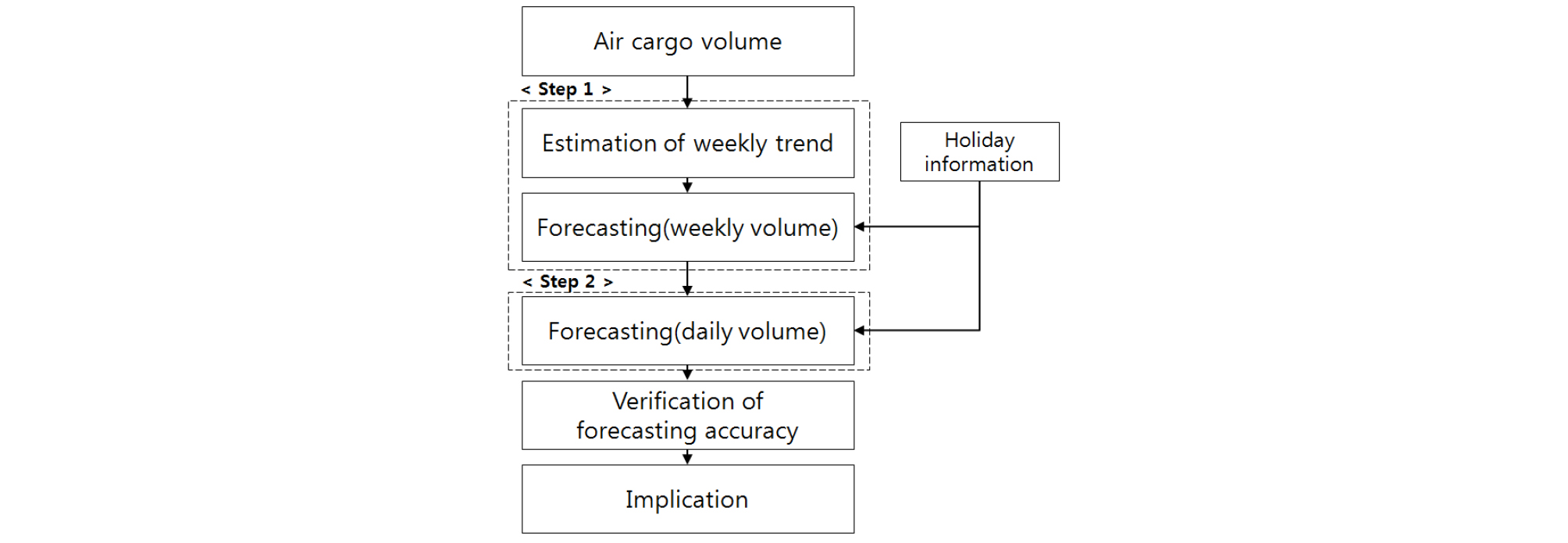
본 연구에서는 앞서 설명한 항공화물 물동량 자료를 바탕으로 총 2단계에 걸쳐 일단위 항공화물 수요예측 모형 개발 과정을 진행하였다.
첫 번째 단계는 일단위 수요예측모형 개발 과정에서 설명변수로 활용된 주단위 물동량 예측을 위한 단계이다. 주단위 물동량 예측을 위한 방법론으로는 Chi-squared Automatic Interaction Detection3) 방법론을 활용하였으며, 설명변수로는 주단위 공휴일 변수와 주단위 물동량의 시계열 예측치를 함께 활용하였다. 시계열 예측치 도출에는 Autoregressive Integrated Moving Average4) 방법론을 활용하였다. 두 번째 단계에서는 앞서 도출한 주단위 물동량 예측치와 주차별 공휴일 및 일자별 휴일 정보를 설명변수로 활용하여 CHAID 방법론을 적용, 최종 일단위 예측모형을 도출하였다.
최종 일단위 예측모형을 도출한 이후에는 예측모형을 바탕으로 향후 56일간의 일자별 물동량 예측치를 추정하였다. 그리고 실제 물동량과의 비교를 통해 예측정확도를 검증하였다. 또한 대표적인 시계열 분석기법은 ARIMA 모형을 통해 추정한 예측치와 예측 정확도를 비교 검증하였다. 나아가 다양한 시점5)으로 예측시점을 이동하면서 본 연구와 동일한 방법론을 활용하여 추정한 각 시점 별 예측모형들의 예측 정확도를 추가 검증함으로써 제안모형이 특정 시점이 아닌 다양한 시점에서 안정적으로 활용가능한지 여부를 확인하였다.
이러한 검증 과정을 통해 본 연구에서 제안한 방법론 및 예측모델의 우수성과 활용 가능성을 확인하였고, 이를 바탕으로 본 연구의 시사점 및 결론을 도출하였다.
선행연구
1. 항공 수요예측 관련 연구
항공운송산업의 특성 상 수요예측은 매우 중요한 분야 가운데 하나이다. 그렇기 때문에 항공수요예측에 대한 광범위하고 다양한 연구 역시 진행되어 왔다. 그러나 대다수의 항공수요 관련 연구들은 화물보다는 여객에 치우쳐져 있다. 예측단위 역시 월, 분기, 년 이상 단위에 대한 거시적 예측이 대부분이다. 방법론의 경우 전통적으로 시계열 모형을 활용한 연구가 주를 이루어져 왔으나, 근래 신경망 모형 등 보다 다양한 방법론을 활용한 연구들이 증가하고 있는 추세이다.
Shin and Lee(2019)는 ARIMAX 및 SARIMAX 모형을 활용하여 국내와 인트라 아시아 국가 간 수출입 항공화물 물동량 예측 모형을 개발하였다. 이를 통해 항공화물 물동량의 긍정적 혹은 부정적인 영향을 미치는 변수들을 확인함과 동시에 설명변수에 따른 국가별 항공화물 물동량 변화에 대한 사전 예측 방안을 제시하였다. Xu et al.(2019)은 Seasonal ARIMA (SARIMA) 모형과 Support Vector Regression (SVR) 모형을 함께 활용하여 항공승객 및 화물에 대한 수요예측을 진행하였다. 첫번째 단계에서 SARIMA 모형을 추정한 이후 SVR 모형을 통해 물동량을 예측하는 과정을 진행하였다. 이를 통해 항공수요예측에 있어 SARIMA와 SVR의 Hybid 모형의 예측정확도를 검증하고 그 활용가능성을 제시하였다. Kim et al.(2019)은 ARIMA-Intervention 모형을 활용하여 국내 공항 전체의 국제선 여객 수요를 예측하였다. 구체적으로 과거 69개의 월별 여객 실적을 대상으로 BIC (Bayesian Information Criterion)와 MAPE (Mean Absolute Percentage Error)를 기준으로 최적 모형을 선정하였다. 그 결과 차기년도의 여객수요는 약 9.3% 가량 증가할 것으로 예상하였다. Lo et al.(2015)은 회귀모형을 활용하여 홍콩국제공항(HKIA)의 항공화물에 대한 수요함수와 공급함수를 추정하였다. 이를 토대로 항공화물에 대한 항공운임과 소득의 탄력성을 추정하였다. 홍공국제공항의 항공화물 수요는 일반적인 물동량과 운임의 관계처럼 운임에 부정적인 영향을 받는 것으로 나타났으나 실제로 그 영향력은 그리 크지 않은 것으로 나타났다. 반대로 소득은 항공화물 물동량의 긍정적인 영향을 미치는 것으로 확인하였으며 2008년 금융위기 이후 항공화물 수요가 운임과 소득에 더욱 민감해졌음을 제시하였다. Min et al.(2013)은 SARIMA 모형을 통해 인천국제공항에서 출발하여 유럽에 도착한 항공화물에 대한 분기별 수요예측을 수행하였다. 구체적으로 SARIMA 모형을 통한 예측 결과와 ARIMA 모형을 통한 예측 결과 간의 상호비교를 통해 SARIMA 모형의 활용성을 검증하였다. 이를 통해 항공화물의 분기별 수요예측에 있어 SARIMA 모형의 활용가치를 제시하였다. Chen et al.(2012)은 Back-Propagation Neural Network (BPN) 모형을 활용하여 일본과 대만 사이의 항공승객 및 항공화물 수요를 예측하였다. BPN을 통해 항공승객 및 화물수요를 동시에 그리고 각각 따로 예측해봄으로써 어느 경우가 예측정확도가 더 높은지 확인하였다. 또한 항공승객 및 화물수요에 동시에 영향을 미치는 변수들과 한 분야에만 영향을 미치는 변수들을 확인하였다. Suryani et al.(2012)은 항공화물터미널의 적정 규모 산정을 위해 system dynamic simulation 모형을 활용하여 시나리오 별 항공화물수요를 예측하였다. 항공화물 수요를 예측하는 과정에서 GDP와 FDI (Foreign Direct Investment)가 항공화물 수요에 영향을 미치는 변수로 나타났으며 구체적으로 모형 내 변수들의 모수를 낙관적인 경우와 보수적인 경우로 구분하여 적용함으로써 각 시나리오별 미래 수요를 예측하였다. Zhang and Zhang(2002)은 항공화물 자유화가 국제항공시장 내 항공화물에 미치는 영향에 대해 논의하였다. 항공여객과 달리 항공화물이 갖는 특수성을 인지하고 항공화물 자유화의 개념과 항공화물 물동량에 미치는 영향에 대해 다양한 관점에서 살펴보았다. 또한 Just in time에 대한 요구 증대와 물류산업 내 수직적 통합으로 인해 항공화물 시장은 더욱 빠른 속도로 성장하였으며, E-commerce가 향후 항공화물 수요를 증가시키는 계기가 될 것으로 예상하였다.
2. 의사결정나무를 활용한 예측 관련 연구
방법론 관점에서 최근 4차 산업혁명의 부상과 더불어 빅데이터(big data)에 대한 관심과 수요가 높아지면서 데이터마이닝(datamining) 기법들에 대한 연구 역시 증가하고 있다. 의사결정나무 방법론은 컴퓨팅 파워 증대에 따른 연산처리 능력 향상과 더불어 직관적이고 해석 및 활용이 용이하다는 장점으로 인해 데이터 마이닝의 주요 방법론으로 각광받고 있다. 실제 의사결정나무 방법론은 자료의 분류와 세분화, 교호작용의 파악, 예측 등 다양한 분야에서 응용되어 활용되고 있으며 의사결정나무 방법론을 활용한 예측에 관한 연구 역시 다양한 분야에서 이루어지고 있다. Jang et al.(2019)은 회귀나무와 이항 로지스틱 회귀분석을 이용하여 통근시간이 길어도 만족도를 높일 수 있는 요인들을 도출하고 분석하였다. 이를 바탕으로 절대적인 통근시간을 줄이기 어려운 경우 통근시간 만족도라는 지표를 통해 통근시간의 질적인 측면을 높일 수 있는 방안 모색에 대한 필요성을 제기하였다. Liu et al.(2017)은 의사결정나무를 활용하여 주요 원자재 가운데 하나인 구리의 가격을 예측하였다. 설명변수로는 유가 및 천연가스, 금, 은, 돈육과 커피의 가격과 더불어 다운존스 지수와 과거 구리의 가격을 활용하였으며 장기와 단기 예측에서 모두 MAPE가 4% 이내로 나타났다. 이를 통해 의사결정나무가 구리 가격 예측에 매우 유용한 방법론임을 밝혔다. Repko and Santos(2017)는 불확실한 수요 하에서 항공사의 효율적인 기재계획 수립을 위한 과정에 나무모형을 활용하였다. 구체적으로 기재계획 수립 간 필요한 예상 물동량 정보를 시나리오 별로 가정하였으며 시나리오 별 물동량 수준을 결정하는 방법론으로 나무모형을 활용하였다. Wu et al.(2017)은 실제 data를 바탕으로 물류시스템 내에서 발생하는 화물손실(cargo loss)에 대해 분석하였다. 연구자들은 전자제품 case를 바탕으로 화물손실의 발생과 연관된 요인들을 확인하기 위해 의사결정나무 방법론을 활용하였다. 이를 통해 운송타입, 제품군, 목적지 등의 요인들이 화물손실의 발생과 연관이 있음을 제시하였다. Amin et al.(2016)은 재생 타이어의 최적화된 closed-loop supply chin network를 설계하였다. 실제 캐나다 토론토의 재생 타이어시장을 대상으로 적용하였으며, 불확실한 상황 하에서 다양한 기간을 대상으로 해당 연구에서 제안하고 있는 네트워크의 수익을 계산하는 과정에 의사결정나무 방법론을 활용하였다. Gharehgozli et al.(2014)은 항만터미널 내에서 컨테이너 야드 내에서 발생하는 재배치(reshuffling) 작업을 최소화하기 위하여 야드 내 새로 유입되는 컨테이너들의 적치방안에 대해 연구하였다. 이를 위해 연구자들은 의사결정트리 휴리스틱 알고리즘을 적용하였으며, 문제의 규모가 커질수록 해당 알고리즘의 효과가 크다는 것을 확인하였다. Yu et al.(2010)은 일본 내 주거목적 건물들의 에너지 사용 지수(Energy Use Intensity)를 예측하는데 있어 의사결정나무 모형을 활용하였다. 온도, 건물타입, 건물자재, 면적, 거주자 수 등 다양한 변수를 설명변수로 활용한 결과 미래 예측에 있어 92%의 정확도를 보였다. 이를 통해 기존의 회귀(regression)모형이나 인공신경망(ANN) 모형 등과 비교하여 예측모형으로서의 의사결정나무의 경쟁력을 강조하였다.
3. 기존연구와의 차별성
기존 항공화물에 대한 수요예측은 주로 월, 분기, 년 단위 이상에 대한 예측이 주를 이루어왔으며, 일 단위와 같이 짧은 단위에 대한 예측은 전무한 상황이다. 긴 예측단위에 대한 항공수요예측은 장기적 관점의 정책, 혹은 전략 수립 등에 도움을 줄 수 있지만 세부적인 운영 효율화 개선에 직접적인 효과를 주기에는 분명한 한계가 있다. 세부적인 운영 효율화를 위해서는 보다 짧은 단위에 대한 수요예측이 요구된다. 그럼에도 불구하고 짧은 단위에 대한 예측에 대한 연구를 찾아보기 어려운 점은 예측단위가 짧아질수록 예측에 대한 어려움이 높아지는 수요예측의 특성 때문이 가장 큰 요인 중 하나라 판단된다. 방법론 관점에서 의사결정나무는 대표적인 데이터마이닝(data ming)기법 가운데 하나로써 이미 다양한 분야에서 활용되고 있으며, 예측 방법론으로서의 범위 역시 넓어지고 있다. 이에 본 연구는 그 동안 항공화물 수요예측 관련 연구에서 찾아보기 어려웠던 일단위 수요를, 역시 항공화물 수요예측 모형개발 간 활용도가 적었던 의사결정나무 방법론을 활용하였다는 점에서 그 의의가 있다. 본 연구에서 제안하고 있는 높은 예측 정확도의 일단위 예측모형에 대한 추가적인 보완과 연구를 통해 항공사, 공항 등 다양한 운영 주체들의 운영효율화 개선에 직접적인 도움을 줄 수 있을 것으로 판단된다. 나아가 의사결정나무 방법론이 예측 방법론으로써 항공화물 분야 뿐 아니라 보다 다양한 물류산업 내 일단위 예측을 대상으로 검토 및 활용될 수 있을 것으로 기대된다.
이론적 고찰
1. 의사결정나무 소개
의사결정나무(Decision Tree)는 데이터마이닝 기법 가운데 하나로 의사결정과정에 적용되는 의사결정 규칙을 나무구조로 구현하여 분석대상을 복수의 소집단으로 분류하고 예측하는 분석기법이다.
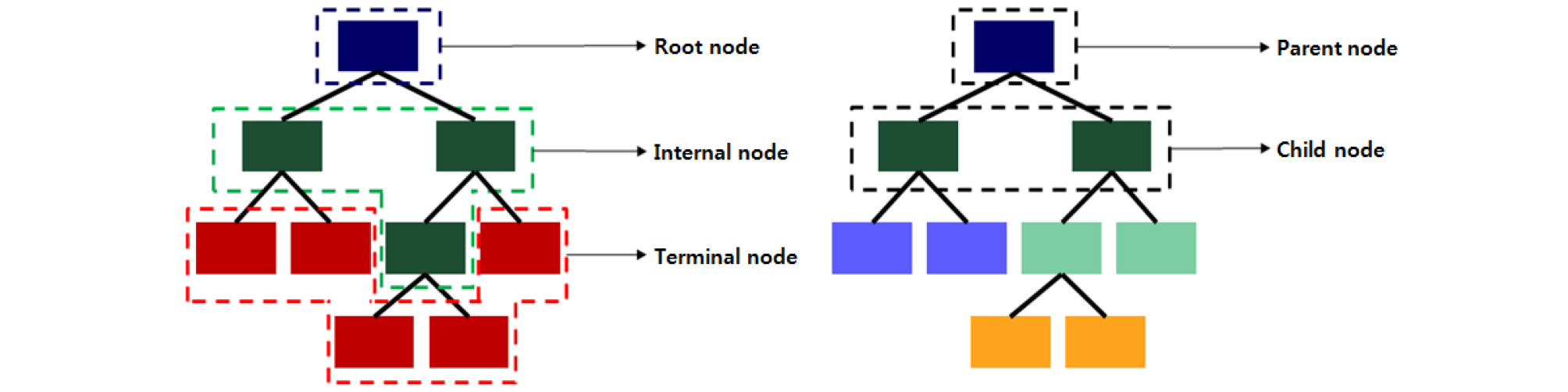
일반적인 의사결정나무의 구조는 Figure 2와 같다.
Figure 2에서 보이는 바와 같이 의사결정나무는 나무구조의 최상단에 위치하는 뿌리마디(root node), 상위노드로부터 분화되는 중간마디(internal node), 더 이상 마디가 분화되지 않은 최종마디인 끝마디(terminal node, 혹은 잎(leaf)), 그리고 마디와 마디를 이어주는 가지(link)로 구성된다. 이때 상위마디를 부모마디(parent node), 그리고 특정 마디 아래로 분화된 하위마디를 자식마디(child node)로 정의한다. 의사결정나무는 분석과정이 나무구조로 구현되며 분석결과가 ‘만약 어떠한 조건A를 만족한 상태에서 다른 조건 B를 만족하면 결과는 C이다.’라는 형태로 해석되기 때문에 기존의 계량분석 방법론들에 비해 상대적으로 분석과정을 쉽게 이해하고 설명할 수 있다는 장점이 있다. 또한 분석을 위해 자료를 따로 가공할 필요가 없으며 대규모의 자료에도 쉽게 적용할 수 있다. 더불어 수치자료와 범주형 자료에 모두 적용할 수 있다는 장점이 있다. 하지만 자료를 제대로 일반화 하지 못할 경우 복잡한 나무모형으로 인한 과적합(overfitting) 문제가 발생할 수 있으며 의사결정나무는 휴리스틱(heuristic) 기법을 기반으로 하고 있기 때문에 추정된 나무모형이 최적의 모형이라 보장하기 어렵다는 단점이 있다. 그럼에도 불구하고 과정과 결과 해석의 용이성, 다양한 활용가능성과 더불어 데이터마이닝 과정에서 자료의 분류와 예측에 매우 효과적인 기법이라는 점에서 다양한 분야에서 그 활용도가 높아지고 있다.
2. 의사결정나무 분석방법
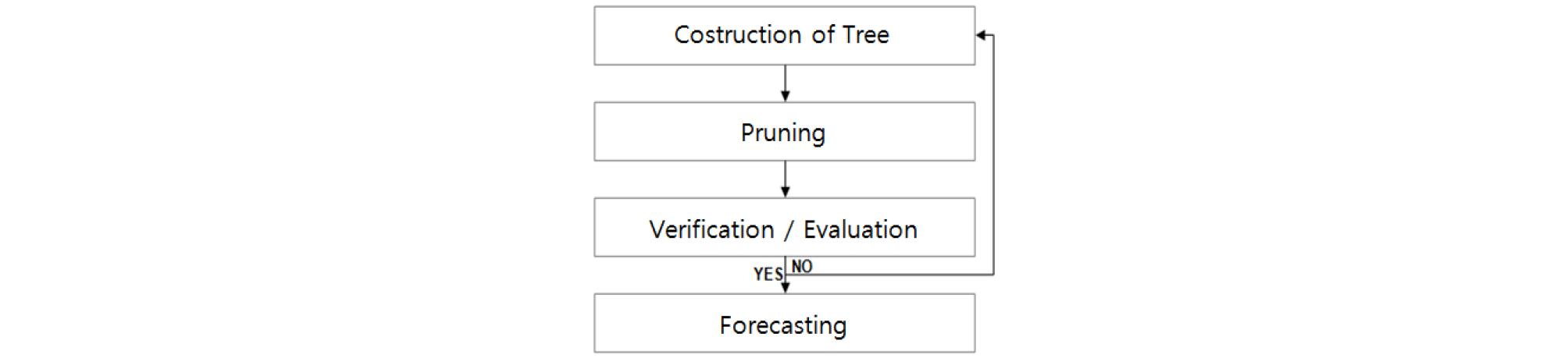
의사결정나무는 목표변수가 명목형 혹은 연속형인지에 따라 분류나무(Classification Tree)와 회귀나무(Regression Tree)로 구분된다. 의사결정나무의 추정은 Figure 3에 나타난 바와 같이 ‘나무의 형성’, ‘가지치기’, ‘타당성 평가’, 그리고 ‘해석 및 예측’의 4단계로 진행된다. ‘나무의 형성’ 단계는 분석 목적과 대상이 되는 자료의 구조에 대한 적절한 ‘분리기준(split criterion)’과 ‘정지규칙(stopping rule)’에 따라 의사결정나무를 형성한다. ‘분리기준’이란 부모마디에서 자식마디들이 생성될 때 증가하는 순수도(purity)를 바탕으로 마디들이 최대의 순수도로 분리될 수 있도록 하는 분리기준이다. ‘정지규칙’이란 특정 마디에서 더 이상 분리를 하지 않고 현재의 마디가 끝마디가 되도록 결정할지 여부를 결정하는 기준을 의미한다. 구체적으로 가지분할의 기준은 분류나무의 경우 Chi-squared 통계량, 지니계수(Gini index), 엔트로피 지수(Entropy index) 등이 활용되며, 회귀나무의 경우에는 F통계량의 F값, 분산감소량 등이 주로 활용된다.
지니계수와 엔트로피 지수에 대한 계산식은 Equations 1, 2와 같다.
| $$\mathrm{Gini}\;\mathrm{Index}\;(i)=\sum_{i=1}^np\left(i\right)\left(1-p(i)\right)=1-\sum_{i=1}^n\left(\frac{n_i}n\right)^2$$ | (1) |
| $$\mathrm{Entropy}\;\mathrm{Index}\;(i)=-\sum_{i=1}^np\left(i\right)log_2p(i)=-\sum_{i=1}^n\left(\frac{n_i}n\right)\log_2\left(\frac{n_i}n\right)$$ | (2) |
여기서, : 가 포함되어 있는 확률
지니계수는 분류된 집합 내 불순도(impurity), 즉, 이질적인 자료들이 얼마나 포함되어 있는지를 측정하는 지표이다. Equation 1을 토대로 만약 집합 내 모든 자료들의 특성이 같다면 의 값은 1의 값을 갖게 되며, 이때 지니계수의 값은 0이 되는 것을 확인할 수 있다. 엔트로피 지수 역시 지니계수와 마찬가지로 불순도를 수치로 나타낸 지수이다. 집합이 완전히 순수한 형태일 경우 Equation 2에서 의 값이 0의 값을 갖는다. 결국 지니계수와 엔트로피 지수 모두 순수한 형태로 분리가 이루어질수록 각각의 수치는 0의 값으로 수렴하게 되며, 해당 수치의 감소폭이 최대화되는 방향으로 가지를 분할하게 된다.
‘나무의 형성’ 단계를 통해 형성된 결정나무를 대상으로 분류오류(classification error) 및 과적합을 방지하기 위해 불필요한 가지를 제거하는 과정을 수행하게 된다. 이를 ‘가지치기’ 단계라 한다. 즉, ‘가지치기’란 가지의 분기수가 일정수준 이상 증가하면 오히려 나무의 정확도가 떨어지는 현상을 방지하기 위한 단계라 할 수 있다.
일반적으로 ‘가지치기’의 기준은 비용함수를 통해 비용이 최소화 되는 수준까지 가지치기를 수행하며, 비용함수는 Equation 3과 같다.
| $$\mathrm{Cost}(T)=Err(T)+\alpha\bullet N(T))=\sum_{i=1}^{N(T)}(y_i-\widehat{y_i})^2+\alpha\bullet N(T)$$ | (3) |
여기서, : 오분류율
: 최종(끝)마디 수
: 가중치
비용함수는 나무의 불순도를 의미하는 와 복잡성을 나타내는 로 구성된다. 비용함수의 궁극적인 목적은 불순도를 최소화하면서 복잡성을 최소화하는 모형을 찾는 것이라 할 수 있으며, 이때 가 와 간의 가중치로 작용한다. 이때 의 값이 커질수록 의 값은 작아지며, 반대로 의 값이 작아질수록 의 값은 커지는 경향이 있다.
‘가지치기’의 단계를 통해 부적절한 가지를 제거한 이후에는, 이익도표(Gain chart), 위험도표(Risk chart), 교차타당성(Cross validation) 등을 통해 나무에 대한 ‘타당성 평가’를 진행하게 된다. ‘타당성 평가’를 통과하지 못한 나무는 필요에 따라 이전 ‘나무의 형성’ 단계로 돌아가 다시 나무를 추정하는 과정을 거치게 되며, ‘타당성 통과’를 최종 통과한 나무의 경우에는 최초 분석의 목적에 따라 ‘해석 및 예측’ 과정에 활용된다.
3. CHAID 방법론
CHAID (Chi-squared Automatic Interaction Detection) 방법론은 1975년 Hartigan(1975)에 의해 개발된 방법론으로 CART (Classification & Regression Tree) 방법론과 더불어 가장 널리 알려진 의사결정나무 방법론 가운데 하나이다. CHAID 방법론은 카이제곱 검정 혹은 F 검정을 이용하여 다지분리(Multiway split)를 수행한다는 점에서 하나의 부모마디 아래 2개의 자식마디 만이 생기는 이지분리(Binary split) 알고리즘인 CART와 차이가 있다. CHAID 방법론은 목표변수가 명목형일 경우에는 Pearson Chi-squared 통계량 혹은 Likelihood Chi-squared 통계량을 분리기준으로 사용한다. 만약 목표변수가 명목형 중에 순서형 혹은 사전의 그룹화된 경우에는 분리기준으로 Likelihood Chi-squared 통계량이 활용된다. 반대로 목표변수가 명목형이 아닌 연속형인 경우에는 F-test를 분리기준으로 활용한다. 그리고 각각의 통계량 가운데 p-value가 가장 작은 예측변수를 선택한 후, 최적분리 기준에 의해 자식마디를 형성시켜 나간다.
Pearson Chi-squared 통계량과 Likelihood Chi-squared 통계랑은 각각 Equations 4, 5와 같이 정의되며 자유도가 인 Chi-squared 분포를 따른다.
| $$x^2=\sum_{i=1}^r\sum_{j=1}^c\frac{(f_{ij}-e_{ij})^2}{e_{ij}}$$ | (4) |
| $$x^2=2\sum_{i=1}^r\sum_{j=1}^cf_{ij}\times\log_e(\frac{f_{ij}}{e_{ij}})$$ | (5) |
여기서, : 관찰치
: 기대빈도,
종속변수가 연속형인 경우에 활용되는 F-test의 통계량은 Equation 6과 같이 표현된다.
| $$F=\frac{MST}{MSE}=\frac{SST/(k-1)}{SSE/(n-k)}=\frac{\sum_{i=1}^n\left(y_i-\overline y\right)^2/(k-1)}{\sum_{i=1}^n\left({\widehat y}_i-\overline y\right)^2/(n-k)}$$ | (6) |
여기서, : 설명변수의 수
: data의 수
모형추정
1. 변수선정
본 연구에서는 앞서 언급한 바와 같이 2단계에 걸쳐 항공화물의 일단위 수요예측 모형을 개발하였다6). 첫 번째 단계에서는 공휴일 변수와 ARIMA 방법론을 활용해 추정한 주단위 예측치를 변수로 활용하였다. 그리고 두 번째 단계에서는 휴일정보와 더불어 첫 번째 단계에서 예측한 예측결과를 설명변수로 활용하였다.
첫 번째 단계에서 활용한 공휴일은 ‘신정’, ‘설날’, ‘삼일절’, ‘근로자의 날’, ‘어린이날’, ‘석가탄신일’, ‘현충일’, ‘광복절’, ‘추석’, ‘개천절’, ‘성탄절’, ‘한글날’ 외에 ‘선거일’, 그리고 ‘임시공휴일’ 등으로 Table 1과 같다.7) 구체적으로 위의 공휴일들을 기준으로 ‘각 주차의 포함된 공휴일 정보’, 해당 주차의 주말 포함 및 비 포함 시 ‘휴일 수’, ‘징검다리 휴일 유무’, ‘각 공휴일의 전후 3주간의 효과’ 등으로 세분한 이후, 설명변수로 모형에 적용하였다. 첫 번째 단계에서 공휴일 정보화 함께 설명변수로 활용된 ARIMA 예측치를 도출하기 위해 추정된 ARIMA 모형은 자료의 안정성을 위해 1차 차분(integrated)된 이후, 자기회귀(Autoregressive, AR)항의 차수는 ‘0’이고, 이동평균(Moving Average, MA)항의 차수가 ‘2’인 ARIMA(0,1,2) 모형이다. Table 2는 추정된 ARIMA(0,1,2)모형의 정보로서 MA(1)과 MA(2)항의 모수(parameter) 값들이 모두 1% 유의수준 이내에서 유의미한 것을 확인할 수 있다. Training 기간의 data를 바탕으로 수립한 ARIMA(0,1,2)모형을 통해 Training 기간과 Forecasting 기간의 주단위 예측치를 도출하여 첫 단계에서의 설명변수로 함께 활용하였다.
Table 1.
List of holiday variables for weekly forecasting
Table 2.
Estimated ARIMA model to forecast weekly volume (trend)
| Coefficient | Standard error | t-value | Sigma | |||
| ARIMA(0,1,2) | AR | - | - | - | - | - |
| MA | MA(1) | 0.602 | 0.048 | 12.664 | 0.00 | |
| MA(2) | 0.294 | 0.048 | 6.19 | 0.00 |
두 번째 단계인 최종 항공화물의 일단위 예측에서는 해당 일자의 ‘요일 정보’, ‘공휴일 여부(주말과의 관계)’ 등으로 반영한 휴일정보와 더불어 첫 번째 단계에서 예측된 항공화물의 주차별 물동량을 설명변수로 함께 활용하여 예측모형을 추정하고 물동량을 예측하였다. 구체적으로 주단위 예측결과물과 함께 설명변수로 활용된 공휴일 변수는 Table 3과 같다.
Table 3.
List of holiday variables for daily forecasting
2. 모형추정
1) 주단위 예측모형
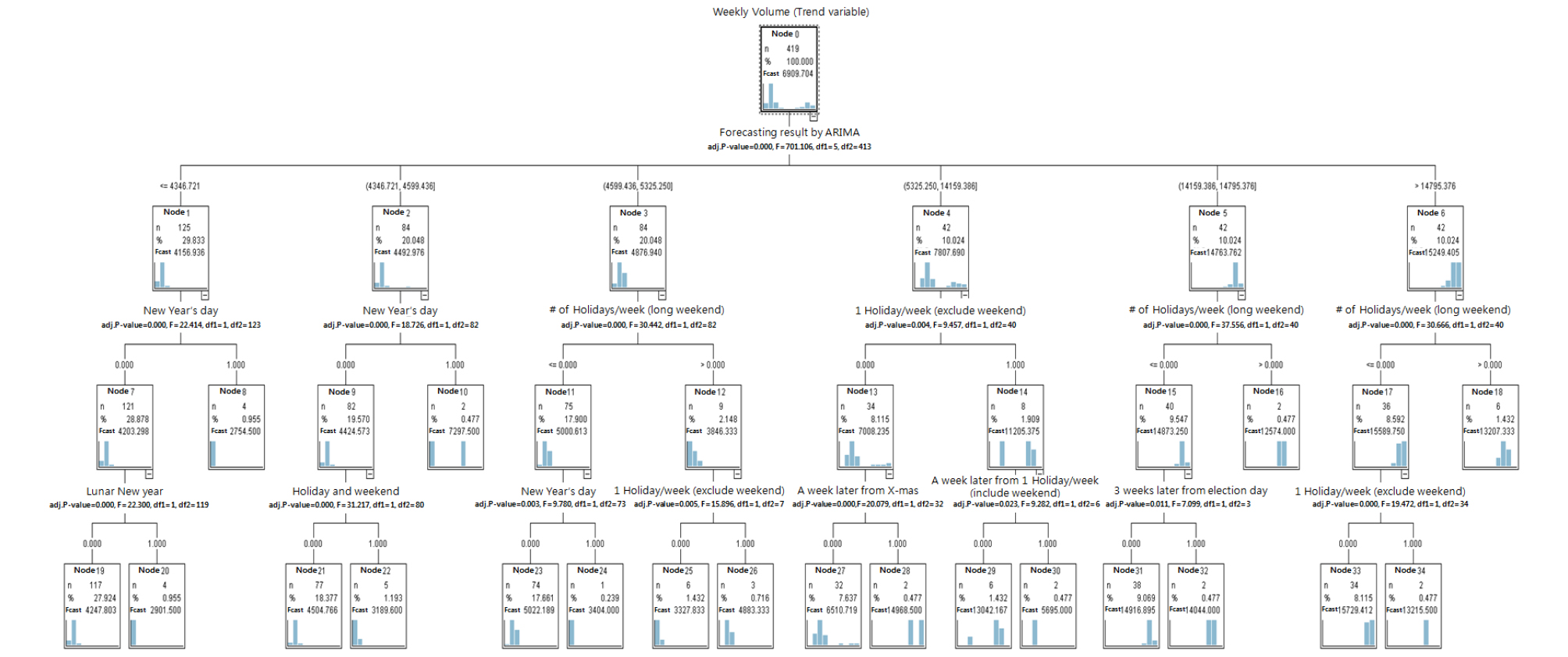
주단위 예측모형은 일단위 예측모형에 활용하기 위한 설명변수인 주단위 예측치를 도출하기 위한 모형으로 CHAID 방법론을 활용하여 모형을 추정하였다. 예측나무(Tree)를 생성하는 과정에서 과적합을 방지하기 위해 나무의 깊이(depth)는 최대 3단계로 정의하였다. 또한 전체 data 가운데 부모마디는 전체의 1%, 자식마디는 최소 0.5%를 만족할 경우에만 분기를 진행하였으며 분할 및 병합을 위한 유의수준은 5%로 하였다8). 해당 기준을 통해 생성된 주단위 예측나무는 Figure 4와 같다.
Table 4는 주단위 예측나무에서 활용된 설명변수들 간의 상대적 중요도를 나타낸 변수 중요도이다. 다양한 공휴일 변수와 함께 설명변수로 활용된 ARIMA 예측치의 상대적 중요도가 0.9130으로 가장 높은 중요도를 나타냈으며, 각 공휴일 별 특성보다는 해당 주차 내 휴일의 수가 상대적으로 더 중요한 것으로 나타났다. 주단위 예측나무의 경우 ARIMA 예측치를 통해 해당 주차에 물동량 수준을 바탕으로 해당 주차와 관련된 공휴일 특성에 따라 세부적인 물동량 수준의 변화량이 결정되는 것으로 나타났다. 그렇기 때문에 전체적인 물동량 수준을 결정하는 ARIMA 예측치의 상대적 중요도가 세부적인 물동량 변화량을 조정하는 공휴일 변수에 비해 높은 것으로 판단된다.
Table 4.
Variable importance of the tree for weekly forecasting
2) 최종 예측모형
본 연구의 최종 목표인 일단위 예측모형을 개발하는 과정에서는 앞서 주단위 예측모형과 동일한 방법론인 CHAID 방법론을 활용하였다. 앞서 주단위 예측나무를 추정하는 과정과 마찬가지로 나무의 깊이는 최대 3단계, 분할 및 분기를 위한 유의수준은 5%로 규정하였다. 또한 전체 data 중에서 부모마디가 차지하는 비중이 1%, 그리고 자식마디는 최소 0.5%를 만족하는 경우에만 분기 및 성장을 진행하였다.9) 마지막으로 앞서 주단위 예측모형을 통해 예측한 주단위 예측치와 Table 3에 정의 되어있는 공휴일 변수를 모형 추정 간 설명변수로 활용하였다.
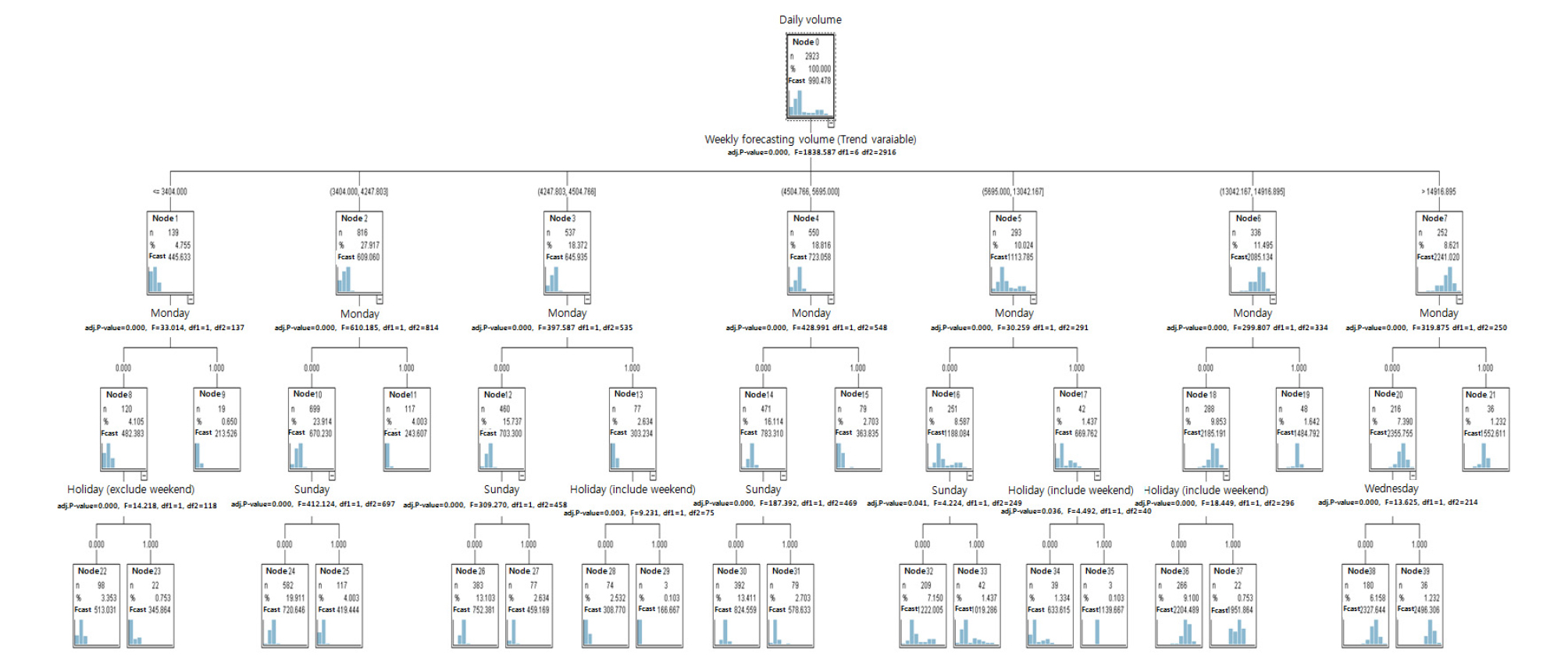
일단위 예측모형으로 최종 생성된 예측나무는 Figure 5와 같다. 일단위 예측나무 Figure 5는 뿌리마디 1개, 중간마디 16개, 끝마디 23개 등 총 40개 마디로 구성되었으며 최초 뿌리마디를 제외하고 총 39개의 노드로 분할 및 성장되었다. 일단위 예측나무에서 최종 선정된 설명변수는 총 6개로 나타났다. 선정된 설명변수들에 대한 변수 중요도 Table 5를 살펴보면 주단위 예측치의 중요도가 0.9038로 가장 높은 중요도를 보였으며, 뒤이어 월요일(0.0709), 공휴일(주말 제외)(0.0078), 일요일(0.0070), 수요일(0.0067), 공휴일(주말 포함)(0.0038) 순으로 나타났다. 주단위 예측치가 해당 시점의 전체적인 물동량 수준을 결정하기 때문에 가장 높은 중요도를 보인 것으로 보인다. 더불어 해당 시점의 주단위 예측치를 토대로 물동량 수준이 결정 된 이후 다양한 공휴일 변수가 각 일자의 세부적인 물동량 수준을 결정하는 것으로 나타났다. 전체 6개 설명변수 가운데 주단위 물동량 변수와 월요일 변수의 중요도 합이 약 0.975로 모형 내에서 두 변수의 중요도가 절대적인 것으로 나타났다.
Table 5.
Variable importance of the tree for daily forecasting
| Variable | Importance | 0 | 0.5 | 1.0 | |||||
| Weekly forecasting volume | 0.9038 |  | |||||||
| Monday | 0.0709 | ||||||||
| Holiday (exclude the weekend)* | 0.0078 | ||||||||
| Sunday | 0.0070 | ||||||||
| Wednesday | 0.0067 | ||||||||
| Holiday (include the weekend) | 0.0038 | ||||||||
Figure 5에서 노드별 물동량 예측치와 설명변수 정보를 살펴보았을 때 우선 일단위 예측을 위한 최초의 분기기준은 주단위 예측치이다. 주단위 예측치의 구간별 수준을 바탕으로 바로 하위 단계에서는 모든 분기에서 월요일 변수가 공통적으로 분리기준으로 활용되었다. 이러한 점은 앞서 변수 중요도를 통해 추론한 내용과 마찬가지로 설명변수들 가운데 주단위 물동량이 가장 중요한 변수인 것으로 나타났으며 바로 다음단계 모든 하위 마디에서 분기 기준으로 활용된 월요일 변수가 다음으로 큰 영향을 미친 것으로 해석할 수 있다. 월요일 효과는 물량 수준과 상관없이 전체 시점에서 나타났다. 구체적으로 예측대상이 월요일인 경우 평균대비 약 48.6%의 물량이 감소하는 것으로 나타났으며, 월요일이 아닌 경우에는 반대로 약 6.3% 증가하는 것으로 나타났다.10) 주단위 물동량 및 월요일 다음으로 중요한 변수로 나타난 공휴일(주말 제외) 효과는 해당 주차의 물동량이 약 3,404톤 이하이면서 해당요일이 월요일이 아닌 경우에만 유의미하게 발생하는 것으로 나타났다. 예측대상이 주말을 제외한 공휴일일 경우 월요일을 제외한 요일의 평균대비 약 28.3%의 물량이 적은 것으로 나타났으며, 반대로 주말을 제외한 공휴일이 아닌 경우에는 약 6.4%의 물량이 증가하는 것으로 나타났다. 그러나 지난 2017년 이후 주차 물동량이 3,404톤 이하였던 경우는 전무하다. 그러므로 해당 효과는 최근에는 거의 없다고 해도 무방하다고 볼 수 있다. 이와는 대조적으로 지난 2년간 물동량에 영향을 미치는 변수로 나타난 것이 바로 수요일 효과이다. Figure 5를 살펴보면 화요일 변수가 분리기준으로 활용된 경우는 ‘노드20’이 유일하다. ‘노드20’은 주단위 물동량 예측치가 약 14,916톤 이상이면서 예측대상 일자가 월요일이 아닌 경우를 의미한다. 일단위 예측모형 추정에 활용된 전체 자료의 기간은 2,933일로 총 419주이다. 이 가운데 주단위 물동량이 14,916톤 보다 많은 경우는 총 51주로 전체기간에 약 12.2%에 불과하다. 그러나 주단위 물동량이 14,916톤을 넘은 51주는 모두 2017년 이후인 것으로 나타났다. 2017년 이후 모형에 활용된 총 95주 가운데 해당 주차들이 차지하는 비중은 약 53.4%이다. 즉 과거에는 보이지 않았던 수요일 효과가 2017년 이후 물동량이 증가하면서 유의미하게 나타난 것으로 판단된다.
모형검증
모형검증 단계에서는 총 3단계의 과정을 통해 본 연구에서 제안하고 있는 모형의 예측 정확도와 더불어 향후 예측 모형으로서 다양한 시점에서의 지속적인 활용 가능성을 검증하였다. 첫 번째 단계에서는 앞서 추정한 일단위 예측모형을 바탕으로 향후 8주, 56일에 대한 일별 예측치와 실적치를 활용하여 모형의 예측정확도를 검증하였다. 두 번째 단계에서는 대표적인 시계열 분석기법인 ARIMA 모형을 활용한 일별 예측치와의 비교를 통해 예측모형으로서의 상대적인 정확도를 비교하였다. 마지막으로 특정 시점에서만 예측정확도를 검증하지 않고 앞서 적용한 방법론과 같은 기준을 적용하여 총 20개 시점에서 해당 시점 별 예측모형을 수립한 후, 각 시점별 예측정확도를 추가 검토하였다. 이는 특정 시점이 아닌 다양한 시점에서의 예측 정확도 검증을 통해 보다 높은 수준의 모형검증을 진행하기 위한 목적이다.
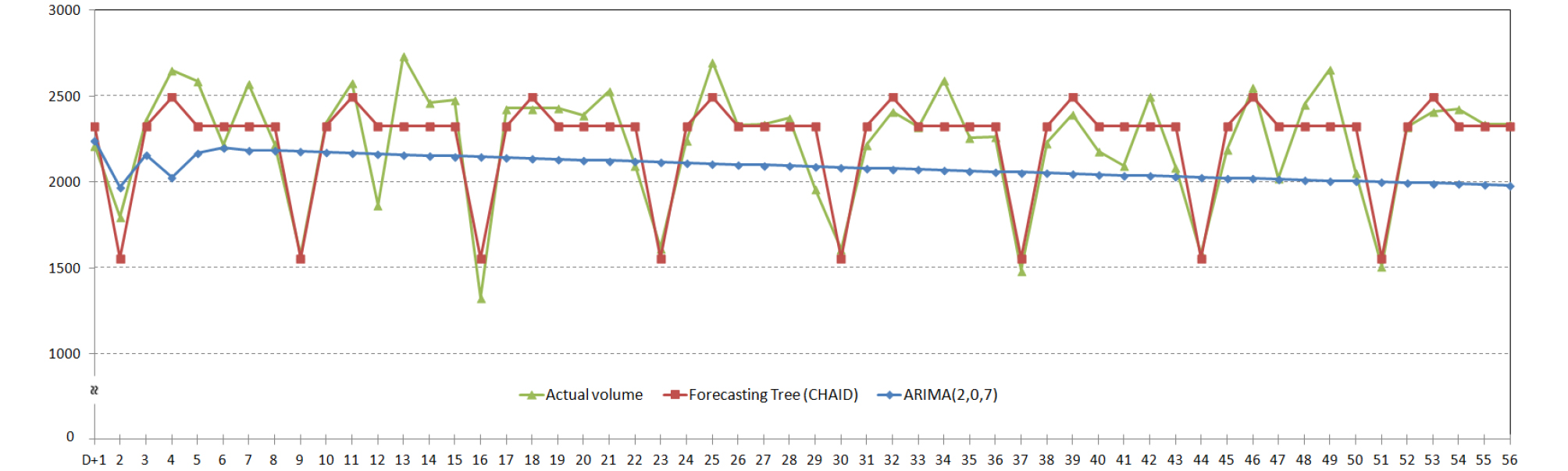
Table 6은 본 연구에서 추정한 일단위 예측나무를 통해 도출한 예측치와 실측치, 그리고 Table 7과 같이 추정된 ARIMA(2,0,7) 모형을 통한 예측치를 비교한 표이다. 예측 1일차에서 마지막 예측시점인 56일차까지의 일평균 예측정확도는 93.9%로 아주 높은 정확도를 보였다. 일반적으로 수요예측은 가까운 시점일수록 보다 높은 정확도를 보이며 시점이 멀어질수록 그 정확도가 급격하게 떨어지는 성향을 보인다. 그러나 본 연구에서 제시한 예측모형의 경우, 마지막 8주차의 일단위 평균정확도가 96.5%를 보이는 등 1일차에서 마지막 56일 차까지 꾸준하게 높은 예측정확도를 보이는 것을 알 수 있다. 또한 ARIMA 모형을 통해 추정한 예측치와 비교하면 일평균 정확도는 약 8.6% 높은 것으로 나타났다. 전체 예측기간 56일 간의 일평균 물동량을 감안한다면 두 모형간의 예측 정확도의 차이는 일평균 약 192톤 이상이라고 할 수 있다. 즉, 본 연구에서 추정한 일단위 예측나무를 활용할 경우, ARIMA(2,0,7) 모형 대비 일평균 192톤 이상 예측오차를 줄일 수 있음을 확인하였다. Figure 6을 살펴보면 예측나무의 경우 예측 1일차에서부터 마지막 56일차까지 실제 물동량과 매우 유사한 결과를 보인 반면, ARIMA 모형의 경우 3일차 이후에는 실제 물동량의 증감 추세를 전혀 반영하지 못하고 1차 함수 형태의 결과를 보였다. 이는 외부 효과에 대한 영향을 반영하기 어려운 ARIMA 모형의 한계가 항공화물 예측 과정에서 역시 나타난 것으로 보여지며, 그 결과 시차가 길어질수록 예측나무와 ARIMA 모형 간의 예측정확도 편차가 더욱 커지는 경향을 보이게 되는 것으로 판단된다.
Table 6.
Forecasting result of the estimated daily forecasting tree and ARIMA(2,0,7) model
Table 7.
Estimated ARIMA model to forecast daily volume
Table 8은 본 연구에서 예측한 시점을 포함해 총 20개의 시점에서 본 연구에서 제안한 방법론과 동일한 방법으로 도출한 20개의 일단위 예측모형들의 평균 예측 정확도이다. 총 20개의 예측시점에서 각각 예측한 56일 간의 평균 예측정확도는 91.2%로 나타났다. 최초 1주차에서부터 마지막 8주차 까지 일단위 평균 예측정확도는 90% 이상을 보이며 앞서 살펴본 Table 6과 마찬가지로 장기 예측에도 높은 정확도를 보였다. 또한 예측시점으로부터의 시차와 상관없이 높은 예측정확도를 꾸준히 유지하는 것을 재차 확인할 수 있다. Tables 6, 8을 바탕으로 본 연구에서 제안한 방법론이 항공화물의 단기 예측과 장기 예측에서 활용성이 매우 높다고 판단되며, 기존의 대표적인 시계열 모형인 ARIMA 모형과 비교해서도 보다 높은 수준의 정확도를 보일 수 있음을 확인하였다. 항공화물의 특성상 단기 예측의 경우 화물 예약정보 등을 통해 높은 수준의 수요예측이 가능할 수도 있다. 그러나 시간이 예측시점이 길어질수록, 또한 예측단위가 분기에서 월, 월에서 주차, 주차에서 일자로 짧아질수록 예측에 의미가 없을 정도로 정확도가 매우 낮아진다. 이러한 특성을 감안하였을 때 본 연구에서 제시한 방법론은 항공화물 수요예측에서 높은 활용도가 기대된다.
Table 8.
Average forecasting accuracy of the forecasting trees on 20 different forecasting points
시사점
본 연구에서는 인천국제공항에서 출발한 K항공사의 일자별 항공화물을 예측하기 위해 의사결정나무 방법론 가운데 하나인 CHAID 방법론과 공휴일 변수를 활용하여 일단위 항공화물 예측모형을 개발하였다. 개발한 예측모형을 활용하여 향후 1일부터 56일까지의 항공화물 수출물동량을 예측하여 검증한 결과, 예측기간 전체의 일별 평균 정확도는 93.9% 수준으로 매우 높은 것으로 나타났다. 최초 1주차의 일단위 평균 예측정확도 92.8%를 시작으로 마지막 8주차의 일평균 예측정확도 96.5%까지 예측시점으로부터의 시차와 상관없이 지속적으로 높은 예측 정확도를 보였다. 이는 기존에 많이 활용되어진 ARIMA 모형을 통한 예측치와 비교해서도 일평균 8.6% 이상의 높은 예측 정확도이다. 이러한 높은 수준의 예측정확도는 특정 예측시점 뿐 아니라 다양한 예측시점에서도 확인할 수 있었다. 예측시점을 1주일 단위로 옮겨가며 총 20개 시점에서 동일한 방법론을 활용하여 각각의 예측모형을 수립하고 예측정확도를 추가로 검증해 보았다. 총 20개 시점에서 각각 예측한 향후 56일간의 전체 예측정확도를 확인해본 결과 약 91.2%의 예측정확도를 보였으며, 이 경우에도 예측시점으로부터의 시차와 상관없이 꾸준히 90% 이상의 정확도를 보이는 것을 확인할 수 있었다. 일반적으로 수요예측은 예측시점으로 시차가 짧을수록 정확도가 높고 시차가 멀어질수록 정확도가 급격히 떨어진다는 특성이 있다. 본 연구에서 제시하고 있는 모형의 경우 시차에 상관없이 높은 정확도가 유지된다는 점에서 매우 고무적이라 할 수 있다.
이러한 높은 예측 정확도와 더불어 본 연구에서 제시하고 있는 모형의 가장 큰 장점은 외부의 설명변수를 활용하지 않는 점이다. 외부 설명변수를 활용한 수요예측의 경우 정확한 수요예측을 위해서는 예측시점에 영향을 미칠 것으로 판단되는 시점의 외부 설명변수들의 정확한 값을 확보해야한다. 아무리 정확한 예측모형을 수립하였다 하여도 설명변수의 값이 제대로 반영되지 않는다면 예측정확도는 떨어지기 마련이다. 본 연구에서는 공휴일 변수와 예측대상이 되는 일단위 물동량의 ARIMA 예측치를 설명변수로 활용하였다. 공휴일 변수의 경우 예측이 따로 필요하지 않으며 일단위 물동량의 ARIMA 예측치의 경우 일단위 물동량 자체의 과거 값들을 활용하기 때문에 외부 변수에 대한 예측이 따로 필요하지 않다는 장점이 있다. 그렇기 때문에 보다 안정적인 예측 정확도를 보일 수 있음과 동시에 변수확보 차원에서 상대적으로 용이하다는 장점이 있다.
결론 및 향후과제
항공화물 수요는 E-commerce의 급격한 성장과 Cross-Border Trade의 확대에 따라 급격하게 증가할 것으로 예상된다. 이에 항공화물 수요예측에 대한 중요성 역시 더욱 높아질 것이라 판단된다. 지금까지 항공화물 수요예측에 관한 절대 다수의 연구들은 주로 일 단위와 같이 짧은 단위가 아닌 월, 분기, 년 단위와 같이 상대적으로 긴 단위에 대한 예측에 대해 이루어져왔다. 이러한 연구들은 항공사의 장기 경영전략 수립, 공항의 인프라 투자계획 수립, 정부차원의 항공운송관련 정책수립 등 다양한 분야에서 매우 유용하게 활용되어 왔다. 하지만 이러한 선행연구들의 경우 항공사나 공항의 실질적이고 세부적인 운영 효율화에 도움을 주기에는 분명한 한계점이 있었다. 실제 항공사, 공항공사 등의 실질적인 운영효율화 달성을 위해서는 긴 단위의 예측보다는 오히려 항공편 혹은 일단위와 같이 보다 짧은 단위의 예측이 더 효과적이기 때문이다. 그러나 수요예측의 특성 상 예측대상의 단위가 짧아질수록 정확한 예측에 대한 어려움은 더욱 커진다. 그동안 항공수요 예측에 관한 연구들 가운데서도 짧은 단위에 대한 예측이 전무하다시피 한 가장 큰 원인 가운데 하나도 이러한 수요예측의 어려움 때문이라 볼 수 있다.
4차 산업혁명의 부상과 함께 빅데이터에 대한 관심이 높아지면서 데이터마이닝 기법들에 대한 연구가 증가하고 있다. 대표적인 데이터마이닝 기법 가운데 하나인 의사결정나무 방법론은 직관적이고 해석 및 활용이 용이하다는 장점으로 인해 다양한 분야에서 각광받고 있으며 자료의 분류와 세분화, 교호작용의 파악, 예측 등 에서 응용 및 활용되고 있다. 본 연구에서는 의사결정나무 방법론 가운데 하나인 CHAID 방법론을 활용하여 항공화물의 일단위 수요예측 모형을 개발하였다. 그리고 본 연구에서 제시한 수요예측 모형이 특정 하나의 시점이 아닌 다양한 시점에서 단기 및 장기 예측 모두에서 매우 높은 예측정확도를 보인다는 사실을 확인하였다. 설명변수의 경우 공휴일 변수와 같이 따로 예측시점에 대해 추가적인 예측이 필요하지 않는 변수와 더불어 다른 외부 변수가 아닌 예측대상 자체의 ARIMA 예측치를 활용한다는 점에서 또한 장점이 있다. 이를 통해 그간 연구 성과가 미진하였던 일단위 항공 수요예측 분야에서 본 연구에서 제시하고 있는 방법론과 예측모형이 매우 유용하게 활용될 수 있는 가능성을 확인할 수 있었다. 이에 본 연구가 향후 항공수요의 일단위 예측과정에서 널리 활용될 것이라 판단되며, 나아가 항공수요 뿐 아니라 일단위 예측이 요구되는 보다 다양한 분야에서 본 연구 결과가 도움이 될 것으로 기대된다.
항공화물 물동량에 영향을 미치는 요인들은 매우 다양하게 존재한다. 항공운임, 유가, 교역량, 공급량(기재 특성 등), 화물특성 등 다양한 요인들이 항공화물 물동량에 영향을 미치고 있다는 사실은 이미 다양한 연구 및 분석들을 통해 지속적으로 확인되었다. 본 연구에서 제시하고 있는 예측모형은 기존에 항공화물에 영향을 미치는 것으로 알려진 주요 변수들을 설명변수로 활용하지 않았다. 다만 ARIMA 예측치 변수에 일정 부분 해당 변수들의 효과가 반영되었다고 판단된다. 또한 해당 변수들이 설명변수로 사용되게 될 경우 예측과정에서 해당 변수들에 대한 예측 혹은 확보가 선행되어야하기 때문에 단순하게 무엇이 더 효율적인지는 판단하기가 매우 어렵다. 이에 다양한 변수들을 활용해보면서 무엇이 더 효과적인지를 확인해 볼 필요가 있다. 또한 data 확보의 어려움으로 인해 본 연구에서 활용하지 못하였지만 항공편 수, 기재 등 공급량과 관련된 변수와 경제변수 및 화물특성과 관련 변수들이 함께 모형에 반영될 경우 예측정확도가 더 높아질 것이라 예상된다. 이에 대한 추가적인 연구의 필요성이 충분하다고 판단된다. 나아가 본 연구에서 제시하고 있는 예측 모형이 단순 항공화물 수출물동량이 아닌 보다 다양한 분야에서 활용될 수 있을 것으로 기대된다.
1)항공사별 일별 물동량의 경우, 공개적으로 확보할 수 있는 유일한 data가 항공정보포탈에서 제공하고 있는 노선 별 수송현황 내 실시간 통계자료이다.
2)2016년 4월 1일부터 2016년 12월 31일 사이의 data는 항공정보포탈 홈페이지 리뉴얼 및 실시간 통계자료 제공시한 등으로 인해 분석 간 미활용.
3)CHAID.
4)ARIMA.
5)20개 시점.
6)IBM SPSS Modeler 17.0 활용.
7)한글날의 경우 법정공휴일로 재지정된 2013년 이후부터 공휴일 변수로 활용하였으며, 분석기간에 있었던 ‘대통령선거일’, ‘지방자지단체장 선거일’, ‘국회의원 선거일’은 모두 ‘선거일’로 통합하여 반영함.
8)마디의 수가 증가할 때 발생할 수 있는 과적합 문제와 복잡성 문제 등을 감안하여 연구자의 판단에 의해 정지규칙을 선정.
9)마디의 수가 증가할 때 발생할 수 있는 과적합 문제와 복잡성 문제 등을 감안하여 연구자의 판단에 의해 정지규칙을 선정.
10)월요일 변수가 적용된 마디와 하위 자식마디들의 물량 증가율을 해당 경우의 data 수로 가중 평균한 수치.