연구배경 및 목적
선행연구 고찰
방법론
1. Two-fluid Model
2. 교통사고 위험 인지 계수의 정의 및 추정 방법
연구 범위 및 데이터
분석결과
1. 종로 지역과 강남 지역의 Two-fluid Model 파라미터 분석
2. 도로망의 기하학적 특성에 따른 거시적 안전성 분석
3. 정지판단속도에 따른 민감도 분석
결론
연구배경 및 목적
Herman and Prigogine(1979)이 제안한 Two-fluid Model은 도시부 도로망의 교통류를 거시적으로 설명하는 모형이다. Two-fluid Model은 주로 도시부 도로망의 운영 성능을 분석하는데 활용되었으나, 근래에 운전 행태 및 안전성 관련 연구에도 활용되었다. 그 중 Dixit(2013)은 Two-fluid Model 파라미터로부터 운전자의 교통사고 위험 인지 분석이 가능함을 해석적으로 제시하였다.
외부 자극에 대한 인간의 신체적 반응은 지각(perception), 식별(identification), 행동판단(judgement, emotion), 반응(reaction, volition) 네 단계의 과정으로 이해할 수 있으며, 교통사고 위험에 대한 운전자의 반응도 같은 이론으로 설명할 수 있다(Doh, 2004). 예를 들어 운전자가 평면곡선을 시각으로 인지하거나 평면곡선 안에서 원심력을 느끼면, 이를 위험으로 식별하고, 위험을 줄이기 위해 의식적으로 또는 무의식적으로 속도를 줄이려는 판단을 내리며, 이를 이행한다. 위험 인지의 정도는 개인 ‧ 상황 ‧ 사회마다 다를 수 있으며, 교통사고 위험 인지 계수의 도입은 이러한 위험 인지의 차이를 표현할 수 있다.
한편, GPS 수신 장치가 보급되면서 GPS 데이터를 활용하여 교통류 상태를 추정하는 연구가 진행되었다. 택시, 버스와 같은 우리나라 사업용 자동차는 교통안전법에 의하여 차량의 GPS 좌표와 속도 등을 기록하는 디지털운행기록계(Digital TachoGraph, DTG)를 장착하여야 한다. 특히, 택시는 도시부 도로망을 순회하는 프로브(probe) 차량의 역할을 할 수 있으므로 택시 DTG 데이터를 활용한 교통류 분석 연구가 활발히 진행되었다.
Two-fluid Model은 교통류를 정지한 차량과 이동 중인 차량으로 이분하는 개념에서 시작하였다. 그러므로 Two-fluid Model 분석 시 정지를 판단하는 기준이 중요하다. 일반적으로 속도가 정지 판단의 기준으로 사용되나, GPS 데이터의 속도는 오차를 포함한다. 따라서 임계값을 도입하여 속도가 임계값보다 작은 경우를 정지로 판단하며, 이 임계값은 정지판단속도(stop speed threshold)라고 지칭되었다(Hong et al., 2003). 그런데 정지판단속도에 따라 Two-fluid Model 파라미터 추정치가 영향을 받는 것으로 알려져 있다(Xiang et al., 2007). Two-fluid Model 파라미터를 활용하는 Dixit(2013)의 모형도 정지판단속도의 영향을 받을 것으로 예상되나, 이에 대한 검토는 수행되지 못하였다.
본 연구는 Dixit(2013)이 제시한 모형을 통해 도시부 도로망의 거시적 안전성 분석이 가능함을 실증 데이터를 통해 확인하고자 하였다. 이를 위해 서울의 대표적인 격자형 도로망인 종로 지역과 강남 지역의 Two-fluid Model 파라미터를 추정하고, 두 지역의 안전성을 도로망의 기하학적 특성과 함께 비교 분석하였다. 또한, 정지판단속도가 분석결과에 미치는 영향을 확인하기 위해 민감도 분석을 수행하였다.
선행연구 고찰
Two-fluid Model은 도시부 도로망의 교통류를 거시적으로 묘사하는 모형이다(Herman and Prigogine, 1979). Two-fluid Model 파라미터로 도시부 도로망의 특성을 상대적으로 평가할 수 있음이 알려지면서(Herman and Ardekani, 1984) Two-fluid Model을 활용하여 교통신호제어시스템의 효과를 분석한 연구와(Jayakrishnan et al., 2000; Jeong et al., 2009; Wu et al., 2011) 날씨가 도로망 성능에 미치는 영향을 분석한 연구가 진행되었다(Lee and Kwon, 2003b). 도로망의 운영성을 결정하는 요소를 찾기 위해 Two-fluid Model 파라미터와 도로망 특성 사이 관계를 회귀 분석한 연구도 있었다(Ayadh, 1986; Ardekani et al., 1992; Ko et al., 2011).
운영성 분석뿐만 아니라 운전 행태와 안전성을 분석하기 위해 Two-fluid Model이 활용되기도 하였다. 공격적(aggressive) 또는 보수적인(conservative) 운전 행태가 Two-fluid Model 파라미터에 영향을 미친다는 것이 밝혀졌으며(Herman et al., 1988), 이러한 Two-fluid Model 파라미터의 성질을 토대로 성별에 따른 운전 행태가 분석되었다(Pande et al., 2015). 안전성 측면 연구에서는 여러 유형의 교통사고율이 Two-fluid Model 파라미터와 높은 상관성을 갖는 것으로 나타났다(Dixit et al., 2011). 이처럼 사례분석을 통해 Two-fluid Model과 운전 행태 및 안전성 사이 관계성을 암시한 연구 결과들이 발표되었으나, 이러한 관계를 연역적으로 설명한 연구는 미비하였다.
한편, 운전자의 위험 인지에 관한 다양한 연구가 수행되었다. 이들은 크게 운전 환경이 운전자의 위험 인지에 미치는 영향을 분석한 연구, 집단 간 위험 인지를 비교하는 연구, 위험 인지와 실제 위험의 괴리를 보인 연구 등으로 분류할 수 있다. 인지란 물리적인 실제 세계가 개인의 정신과정으로 수용되는 것을 의미한다(Dixit, 2013). 이를 직접 관찰하는 것은 어려우므로 주로 설문조사를 통한 위험 인지 연구가 이루어졌다. Kim et al.(2014)은 설문조사를 통해 교통사고 위험요인을 조사하였다. 조사 결과에 따르면 운전자들은 평면곡선, 종단곡선, 주변 차량의 난폭운전으로부터 위험을 인지하고, 시거, 차로 수, 교통량에 따라 주행속도를 변화시키는 것으로 나타났다. 그 밖에 피부 감지기와(Taylor, 1964) 시선 추적기(eye tracker)를 이용하여(Charlton et al., 2014) 운전자의 무의식적 위험 인지를 분석한 연구와, 주행속도를 관찰하고 속도 선택 모형에 적용하여 위험 인지를 분석하는 연구도 수행되었다(Tarko, 2009).
도로의 특성으로부터 교통사고 발생 빈도 또는 심각도를 예측하는 계량경제모형도 꾸준히 연구되었다. 교차로에 대한 연구에서는 차로 수가 많을수록 교통사고 발생 빈도(Park et al., 2008) 및 심각도(Ryu and Lee, 2004)가 높아지는 것으로 나타났다. 간선도로 축에 관한 연구에서는 교차로가 많고, 교통량이 많을수록 교통사고가 발생할 가능성이 높다는 결과가 도출되었다(Won et al., 2006). 이러한 모형을 활용하기 위해서는 분석 지점의 기하학적 특성을 사전에 수집해야 하지만, Two-fluid Model은 이러한 정보를 필요로 하지 않으므로 Two-fluid Model은 안전성 분석의 새로운 방법론을 제시할 수 있다.
Dixit(2013)은 Two-fluid Model을 활용하여 운전자의 교통사고 위험 인지를 분석할 수 있음을 해석적으로 제시하였다. 운전자는 본인의 효용을 최대화시키는 속도를 선택한다는 이론인 속도 선택 모형에 교통사고 위험 인지 계수를 도입하였으며, 이를 Two-fluid Model과 통합하였다. 사례 분석에서는 Two-fluid Model 파라미터로부터 교통사고 위험 인지 계수를 추정하였고, 도로망의 특성이 운전자의 교통사고 위험 인지에 미치는 영향을 분석하였다. 그러나 데이터의 한계로 개별 도시가 아닌 21개의 도시의 통합적인 교통사고 위험 인지 계수만을 제시하였다.
GPS 수신 장치의 보급으로 GPS 데이터를 활용한 교통류 분석 연구가 활발히 진행될 수 있었다. 대표적으로 통행시간을 추정하거나(Quiroga and Bullock, 1998; Chung and Choi, 1999; Shim and Choi, 2006) 대기행렬길이를 추정하는 연구가 수행되었다(Cheng et al., 2011). 택시 DTG 데이터도 통행시간 추정 연구(Lu et al., 2016), 통과교통량 추정 연구(Kwon and Kim, 2018), Macroscopic Fundamental Diagram 도출 연구(Geroliminis and Daganzo, 2008; Lu et al., 2018)에 활용되었다. 택시 DTG 데이터를 비롯한 GPS 데이터를 활용하여 Two-fluid Model 파라미터를 추정하는 연구도 다수 수행되었다(Lee and Kwon, 2003a; Zeng, 2015; Kwon et al., 2019).
GPS 데이터를 활용한 안전성 연구도 진행되었다. 가속소음(acceleration noise) 등 안전성 지표를 GPS 데이터로부터 산출할 수 있었고(Ko, 2006; Boonsiripant, 2009), 이웃한 두 차량의 측위를 통해 안전성을 평가할 수 있었다(Williams et al., 2012; Park et al., 2017). 교통사고가 발생하기까지 주행거리를 변수로 한 생존분석을 수행하기 위해 GPS 데이터를 활용한 연구가 있었다(Ayuso et al., 2016). 이처럼 GPS 데이터를 활용한 안전성 연구가 다수 수행되었으나, GPS 데이터를 활용하여 도로망의 안전성을 거시적으로 분석한 경우는 많지 않았다.
따라서 본 연구는 택시 DTG 데이터로부터 Dixit(2013) 모형의 교통사고 위험 인지 계수를 추정하여 개별 지역의 거시적인 도시부 도로망 안전성 분석이 가능함을 보이고자 한다.
방법론
1. Two-fluid Model
Two-fluid Model은 두 가지 가정에 기초하고 있다. 첫째, 도로망 내 차량들의 평균주행속도(vr)는 주행차량비율(fr)에 비례한다(Equation 1). 둘째, 도로망 내 정지차량비율(fs)은 도로망을 순회하는 프로브 차량의 정지시간비율과 같다(Equation 2).
| $$v_r=v_mf_r^{\;n}=v_m(1-f_s)^n\;\;(f_r+f_s=1)$$ | (1) |
| $$f_s=T_s/T\;\;(T_r+T_s=T)$$ | (2) |
여기서, vr: 평균주행속도
vm: 평균최대통행속도
fr: 주행차량비율
fs: 정지차량비율
n: Two-fluid Model 파라미터
Ts: 단위거리 당 평균정지시간
Tr: 단위거리 당 평균주행시간
T: 단위거리 당 평균통행시간
Equations 1, 2로부터 Two-fluid Model의 모형식이 도출된다(Equations 3, 4).
| $$T_r=T_m^\frac1{n+1}T^\frac n{n+1}$$ | (3) |
| $$\ln T_r=\frac1{n+1}\ln T_m+\frac n{n+1}\ln T$$ | (4) |
Tm은 단위거리 당 평균최소통행시간을 의미하며, 혼잡이 없는 이상적인 상황일지라도 신호제어와 같은 교통운영요소가 미흡한 도로망은 높은 Tm값을 가질 수 있다. n은 단위거리 당 평균정지시간(Ts) 또는 정지차량비율(fs)이 증가함에 따라 단위거리 당 평균통행시간(T)이 증가하는 정도를 나타내는 파라미터이다. 낮은 n값은 교통수요가 증가하여도 도로망의 운영상태가 쉽게 악화되지 않음을 의미한다. 따라서 Tm과 n은 도시부 도로망의 성능을 거시적으로 나타내는 지표로 사용될 수 있다.
Two-fluid Model 파라미터인 Tm과 n을 산출하기 위해 우선 프로브 차량의 운행 기록을 일정한 크기의 microtrip으로 분할해야 한다. microtrip의 크기는 거리 기준 또는 시간 기준으로 정할 수 있으며, 기존 연구는 주로 1mile의 거리를 기준으로 분석하였다(Herman et al., 1988; dekani et al., 1992; Hong et al., 2003; Dixit et al., 2011). 각 microtrip의 Tr과 T를 산출하고 Equation 4의 로그선형회귀모형을 통해 Two-fluid Model 파라미터인 Tm과 n을 추정할 수 있다.
2. 교통사고 위험 인지 계수의 정의 및 추정 방법
소비자가 기대효용(expected utility)을 최대화하는 행동을 선택한다는 개념은 경제학에서 널리 사용되고 있다(Parkin and Wu, 1972). 운전자가 겪는 사건 또는 상태(state)는 교통사고 발생과 미발생 두 가지라고 가정할 수 있다. Dixit(2013)의 속도 선택 모형은 교통사고 발생 ‧ 미발생이라는 상태를 확률적으로 인지하는 운전자가 기대효용을 최대화시키는 주행속도를 선택한다는 가정으로 구성되었다.
| $$v_r=\arg\;\max\nolimits_{v_r}E\lbrack u\rbrack$$ | (5) |
| $$E\lbrack u\rbrack=P_{no\;crash}u_{no\;crash}+P_{crash}u_{crash}$$ | (6) |
여기서, vr: 평균주행속도
E[u]: 기대효용
Pcrash: 운전자가 인지하는 교통사고 발생 확률
Pno crash: 운전자가 인지하는 교통사고 미발생 확률
ucrash: 교통사고 발생 시 운전자가 인지하는 효용
uno crash: 교통사고 미발생 시 운전자가 인지하는 효용
Equation 6에서 각 항을 살펴보면, 먼저 운전자가 인지하는 교통사고 발생 확률(Pcrash)은 Equation 7과 같이 주행시간비율(fr)에 대해 단조증가하는 함수로 모형화되었다.
| $$P_{crash}=\alpha f_r^{\;\beta}=\alpha(T_r/T)^\beta=\alpha(v/v_r)^\beta$$ | (7) |
여기서, α: Baseline Perceptions of Causing a Crash
β: Perceived Crash Likelihood Factor (β>0)
vr: 평균주행속도
v: 평균통행속도
Equation 7의 경계 조건에서, 주행시간비율(fr)이 0일 때 운전자가 인지하는 교통사고 발생 확률(Pcrash)은 0이다. 운전자가 주행하지 않는다면 교통사고 발생 확률이 0이라고 볼 수 있으므로, 이러한 경계조건은 합리적으로 보인다. Perceived Crash Likelihood Factor (β)는, 같은 fr에서, 그 값이 작을수록 운전자가 교통사고 발생 확률을 높게 인지함을 나타낸다. α는 속도 선택에 영향을 미치지 않는다.
운전자가 인지하는 교통사고 미발생의 확률(Pno crash)은 여사건의 확률인 Equation 8로 나타난다.
| $$P_{no\;crash}=1-P_{crash}=1-\alpha f_r^{\;\beta}$$ | (8) |
통행 의사결정에서 중요한 역할을 하는 통행시간은 초기의 속도 선택 모형 연구부터 고려되고 있었다(Mohring, 1965). Tarko(2009)도 통행속도에 대한 감소함수를 부효용 모형에 포함하고 있었다. Dixit(2013)은 교통사고 미발생 시 운전자가 인지하는 효용(uno crash)을 평균통행속도(v)로 하였다.
| $$u_{no\;crash}=v$$ | (9) |
일반적으로 속도가 높을수록 교통사고 심각도가 높다. Elvik et al.(2004)이 제시한 지수 모형(Power Model)과 고전 물리학의 운동에너지 공식을 고려하면 교통사고 심각도는 속도에 대한 지수함수의 형태로 가정함이 타당하다. Dixit(2013)은 교통사고 발생 시 운전자가 인지하는 효용(ucrash)을 Equation 10과 같이 구성하였다.
| $$u_{crash}=-wv_r^{\;k}$$ | (10) |
여기서, w: Crash Weighting Factor (w>0)
k: Perceived Impact Factor (k>1)
Crash Weighting Factor (w)는, vr과 k가 같을 때, 그 값이 클수록 운전자가 교통사고 부효용(disutility)을 크게 인지함을, 즉 교통사고 심각도를 높게 인지함을 나타낸다.
Equation 5에서 기대효용의 최대를 구하기 위해 미분계수가 0인 점을 찾으면 Equation 11과 같이 운전자가 선택하는 평균주행속도를 구할 수 있다. 이를 Equation 12와 같이 치환하면 Tm, n, β, w에 관한 관계식인 Equation 13이 유도된다.
| $$\beta v=(k-\beta)wv_r^{\;k}\;\;(k>\beta)$$ | (11) |
| $$v=\frac1T,\;v_r=\frac1{T_r},\;k=1+\frac1n\;where\;n>0$$ | (12) |
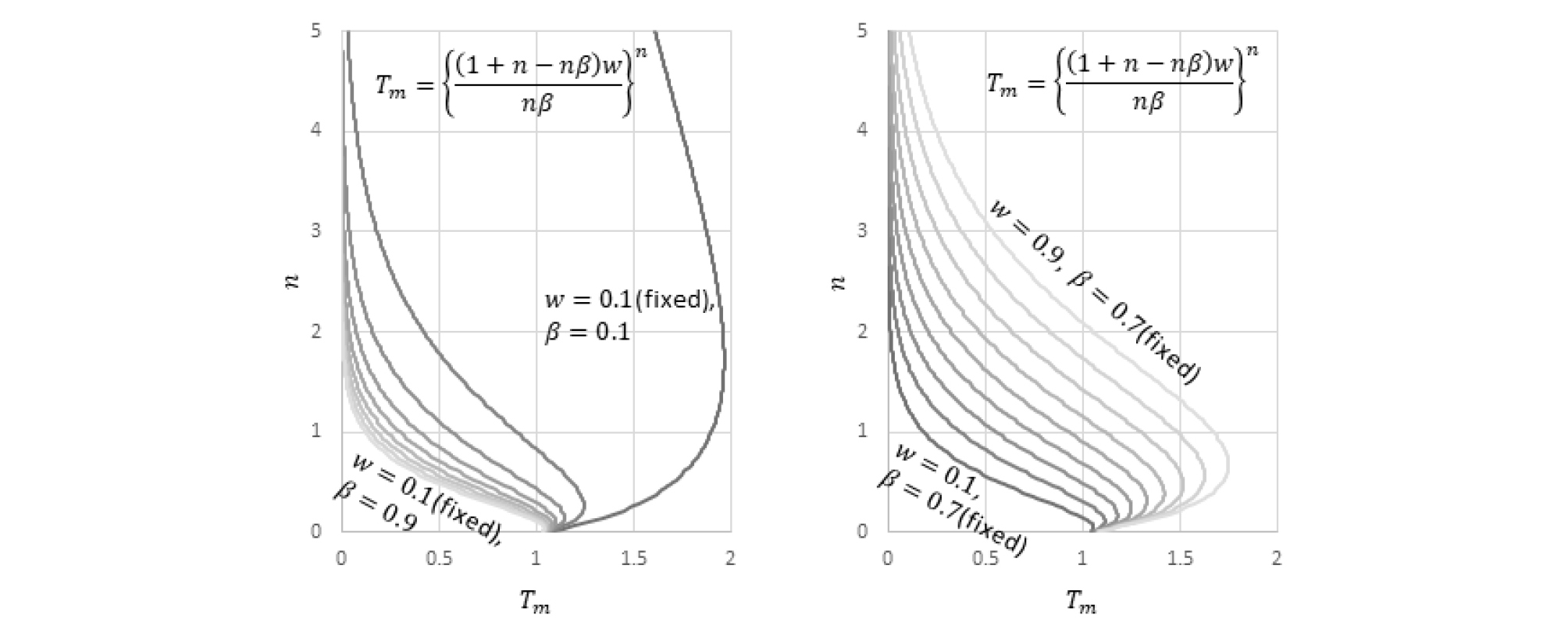
| $$T_m^{\;\frac1n}=\frac w\beta\frac1n+\frac w\beta-w\;\mathrm{or}\;T_m=\left\{\frac{(1+n-n\beta)w}{n\beta}\right\}^n\;\;$$ | (13) |
Equation 13을 그래프로 나타내면 Figure 1과 같다. w가 클수록, β가 작을수록 Tm-n그래프는 우상향으로 이동하는 성질이 있다. 즉, 순서쌍 (Tm, n)이 우상단에 있을수록 β가 작아지거나 w가 커질 것으로 예상할 수 있으며, 그러한 도로망은 교통사고 발생확률 또는 심각도가 높을 것으로 추론할 수 있다.
α, β, w, k 모두 운전자의 교통사고 위험 인지를 함의한다. 그러나 α는 속도 선택과 무관하기 때문에 그 값을 산출할 수 없고, k는 n에 의해 결정되므로 독립된 변수로 볼 수 없다. 따라서 본 연구는 β와 w를 교통사고 위험 인지 계수라고 지칭하였다.
Two-fluid Model 파라미터로부터 β와 w를 추정하기 위해 본 연구는 Equation 14와 같은 수리계획법을 고안하였다. Dixit(2013)이 제시한 선형회귀분석으로는 β 또는 w가 음수로 도출될 우려가 있으며, 이는 계수의 정의에 부합하지 않기 때문이다.
Dixit(2013)의 선형회귀분석과 본 연구가 제시한 방법 모두 오차제곱합 최소화를 목적으로 하므로 두 방법론이 개념적으로 대동소이하다. 이때, 한 도로망의 교통사고 위험 인지 계수를 추정하기 위해 다수의 Two-fluid Model 파라미터 순서쌍을 필요로 한다.
연구 범위 및 데이터
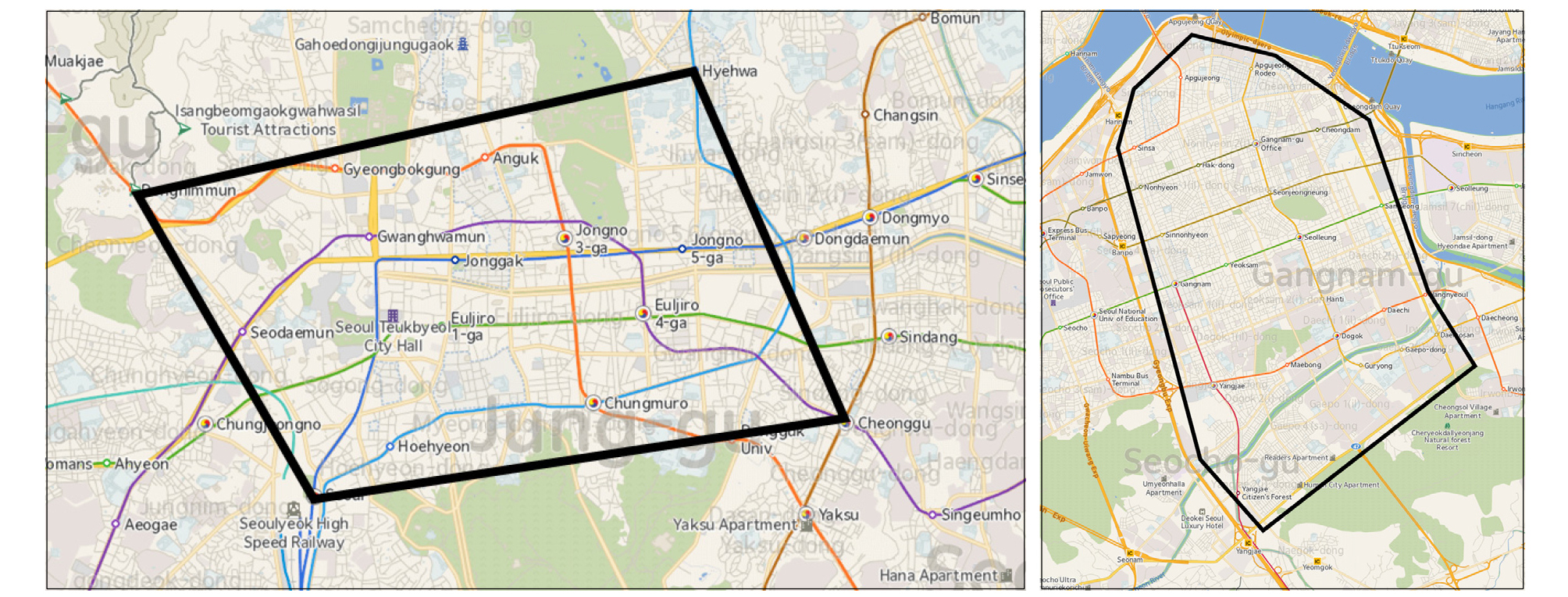
본 연구는 서울시의 도심이며 격자형 도로망을 갖는 대표적인 지역인 종로와 강남 지역을 공간적 범위로 선정하였다. Figure 2와 같이 종로는 사대문 내부를 기준으로, 강남은 도시고속도로를 포함하지 않도록 지역을 설정하였다.
Two-fluid Model 파라미터를 산출하기 위해 2018년 11월 09일부터 2018년 11월 30일까지 22일간의 서울시 택시 DTG 데이터를 활용하였다. 택시 DTG 데이터는 Table 1과 같이 택시 차량 ID, 경도, 위도, 고도, 일시, 조향각, 속도, 승객재차여부 8개의 열로 이루어져 있다. 경위도 좌표는 도(°, degree) 단위이며 107이 곱해져 기록된다. 속도는 kph 단위의 정수로 저장된다. 일시 열에 나타난 바와 같이 각 택시는 10초마다 차량 상태를 기록한다. 승객재차여부 열에서 1은 승객이 재차 중인 상태, 0은 승객이 없는 공차 상태를 의미한다. 공차 상태의 데이터는 택시가 승객을 탐색하거나 택시 정류장에서 대기하는 기록이 포함되어 있으므로, 합리적인 운전 행태를 반영하기 위해 승객이 재차 중인 상태의 데이터만을 분석에 사용하였다. 또한 심야시간에는 과속이나 휴식과 같이 주변 교통류 상태를 모사하지 않는 기록이 포함될 우려가 있으므로 23시부터 익일 05시까지 데이터는 분석에 제외하였다. 결과적으로, Table 2와 같이 종로 지역에는 일평균 4백만 여 개의 데이터를, 강남 지역에는 일평균 7백만 여 개의 데이터를 분석에 활용할 수 있었다.
Table 1. An example of Seoul taxi DTG dataframe
Table 2. Daily average number of vehicles and records in filtered Seoul taxi DTG data
| Region | Vehicles | Records |
| Jongno | 31,722 | 4,040,468 |
| Gangnam | 35,032 | 7,126,249 |
이렇게 얻어진 데이터를 택시 차량 ID와 일시에 대해 정렬한 후, 인접한 두 쌍의 경위도 좌표로부터 10초 간 이동거리를 산출하고 1.5km microtrip으로 분할하였다. 즉, 연속된 데이터의 누적 이동거리가 1.5km 이상 될 때마다 해당 데이터를 하나의 microtrip으로 추출하였다. 각 microtrip에 정지판단속도 0kph를 적용하여 단위거리 당 평균주행시간(Tr)과 단위거리 당 평균통행시간(T)을 산출하고 Two-fluid Model 파라미터를 추정하였다.
분석결과
1. 종로 지역과 강남 지역의 Two-fluid Model 파라미터 분석
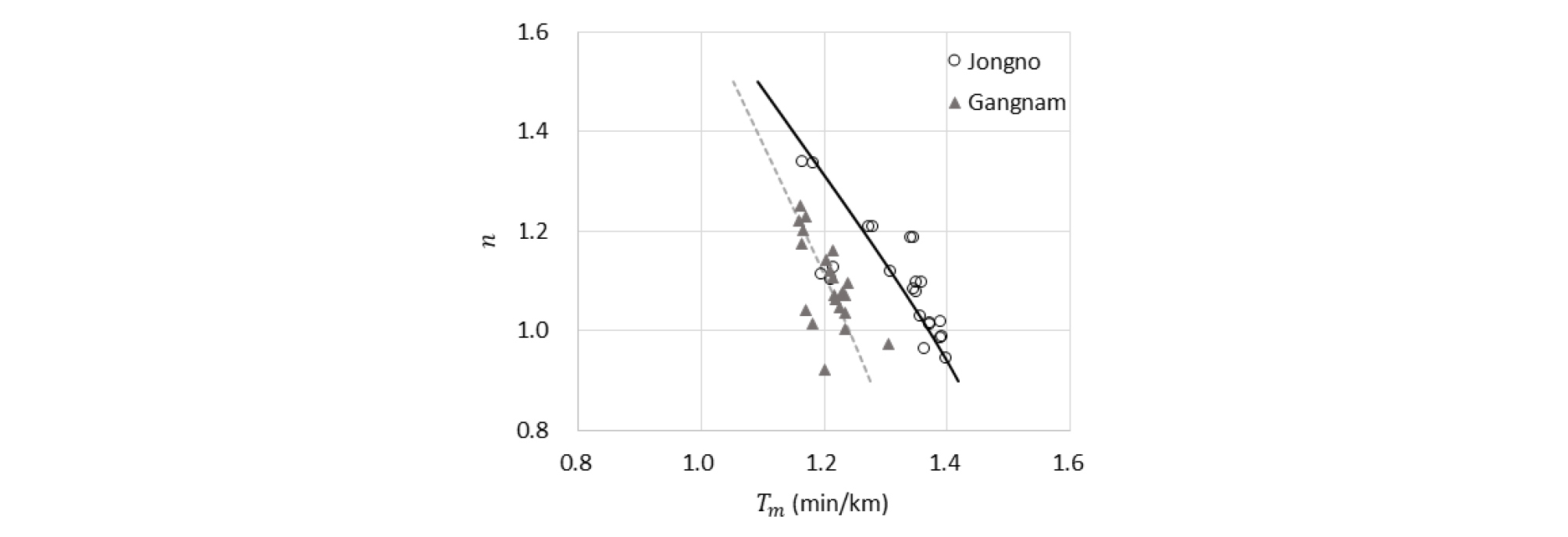
평균적인 Tm값은 종로 지역이 1.32min/km, 강남 지역이 1.21min/km로 종로에서 더 높았으며, 이는 비혼잡 시 도로망의 운영성이 종로보다 강남에서 더 양호함을 의미한다. 두 지역의 평균적인 n값은 종로 1.10, 강남 1.10으로 동일하였으므로 교통수요의 증가에 따른 도로망 성능 악화 정도는 두 지역에서 비슷한 것으로 보인다. Table 3에 따르면 같은 지역일지라도 날짜에 따라 Two-fluid Model 파라미터 추정치가 변하였는데, 택시 DTG 데이터는 전수가 아닌 표본 데이터이며, 요일별로 교통신호 계획 및 운전자의 운전 행태가 동일하지 않기 때문으로 판단된다.
Table 3. Two-fluid model parameters of Jongno and Gangnam (Tm: min/km)
Figure 3에 지역별 Two-fluid Model 파라미터를 Equation 13에 적합(fitting)시킨 곡선을 도식하였다. 점군과 곡선의 위치가 다른 것으로 보아 두 지역의 Perceived Crash Likelihood Factor (β)와 Crash Weighting Factor (w)가 다르게 추정될 것으로 예상되었다.
2. 도로망의 기하학적 특성에 따른 거시적 안전성 분석
본 연구는 종로와 강남에서 차이가 있는 기하학적 특성으로 평균 차로 수와 교차로 밀도를 선정하였다. 그리고 두 가지 특성이 도로망의 안전성에 미치는 영향이 교통사고 위험 인지 계수를 통해 나타나는지 확인하였다.
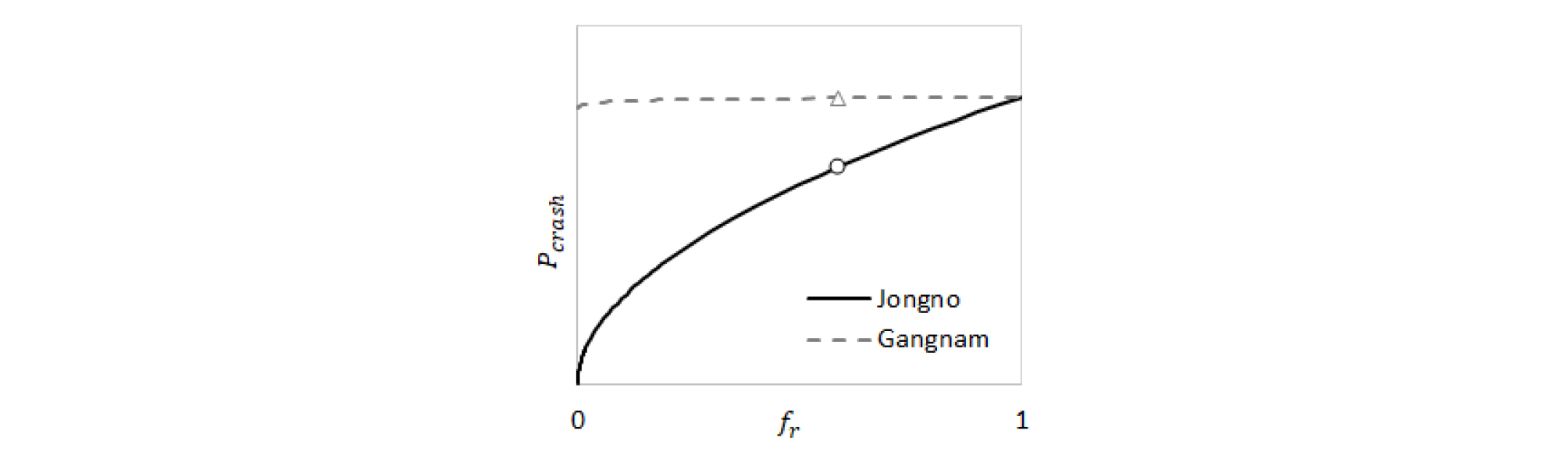
Park et al.(2008)과 Kim et al.(2014)의 연구를 고려하면, 강남은 종로보다 평균 차로 수가 24% 많으므로 강남에서 교통사고 발생확률이 높을 것으로 예상할 수 있었다. Perceived Crash Likelihood Factor (β)는 Table 4와 같이 종로에서 0.525, 강남에서 0.006으로 추정되었다. Pcrash 함수의 그래프와 함숫값을 도식한 Figure 4에 의하면, 종로보다 β가 낮은 강남의 교통사고 발생확률은 종로보다 높은 것으로 나타났다. 이렇듯 기존 연구와 일관된 결과는 β를 통한 도로망의 안전성 분석이 가능함을 시사한다. 또한, 우리나라 교통사고분석시스템(Traffic Accident Analysis System, TAAS)에서 구득한 자료에 따르면 인구 10만 명 당 교통사고 발생 건수는 2018년 기준 종로보다 강남에서 많았다. 이를 통해 β의 함의가 통계자료와도 일치함을 확인하였다.
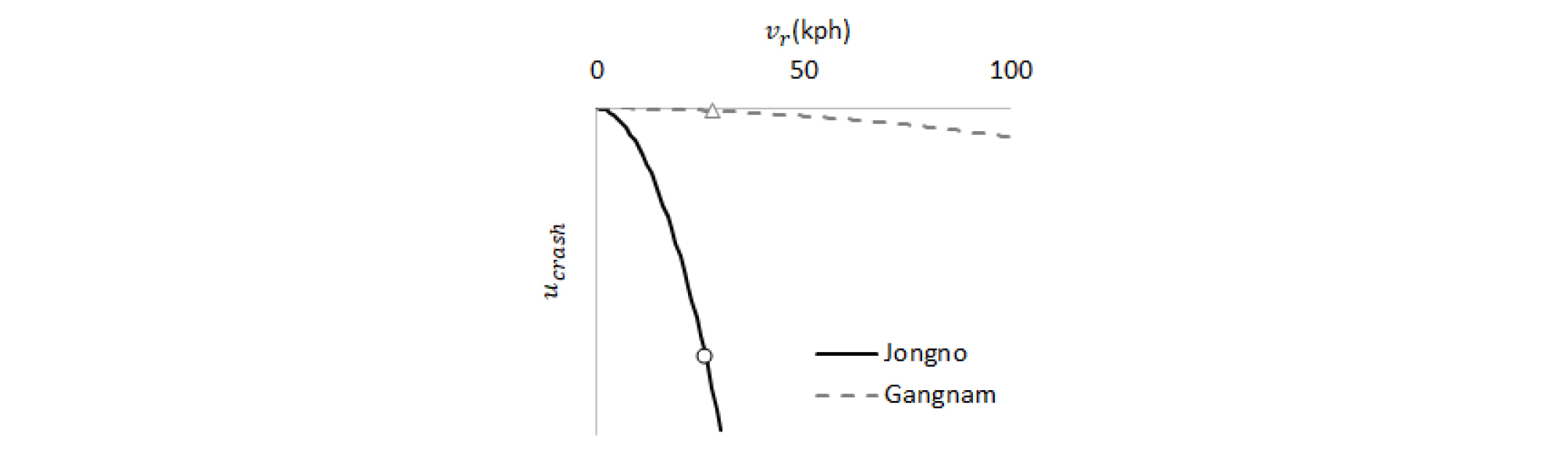
Table 4. The number of lanes, probability of a crash, and accident statistics
| Region |
Average number of lanes | β | fr | Pcrash=αfrβ |
Accident per 100 thousand capita* |
| Jongno | 1.92 | 0.525 | 0.590 | 0.758α | 3,923 |
| Gangnam | 2.39 | 0.006 | 0.589 | 0.997α | 4,136 |
강남은 종로보다 평균 교차로 밀도가 6% 낮으므로 Won et al.(2006)에 의하여 강남은 종로보다 교통사고 심각도가 낮을 것으로 예상할 수 있었다. Crash Weighting Factor (w)는 Table 5와 같이 종로에서 0.448, 강남에서 0.004로 추정되었다. Figure 5에 도식한 ucrash 함수의 그래프와 함숫값에 따르면, 종로보다 w가 낮은 강남은 교통사고 심각도가 낮게 나타났다. 기존 연구와 w 추정의 일관된 결과는 w를 통한 도로망의 안전성 분석이 가능함을 시사한다. 2018년 기준, TAAS에서 구득한 인구 10만 명 당 사망자 수도 종로보다 강남에서 적었으므로, w의 함의가 통계자료와도 일관됨을 확인하였다.
Table 5. Intersection density, utility of a crash and accident statistics
| Region |
Intersection density (km-1) | w | vr (kph) | ucrash = -wvrk |
Fatality per 100 thousand capita* |
| Jongno | 1.07 | 0.448 | 26.18 | -248.068 | 5.0 |
| Gangnam | 1.00 | 0.004 | 27.87 | -2.206 | 3.6 |
3. 정지판단속도에 따른 민감도 분석
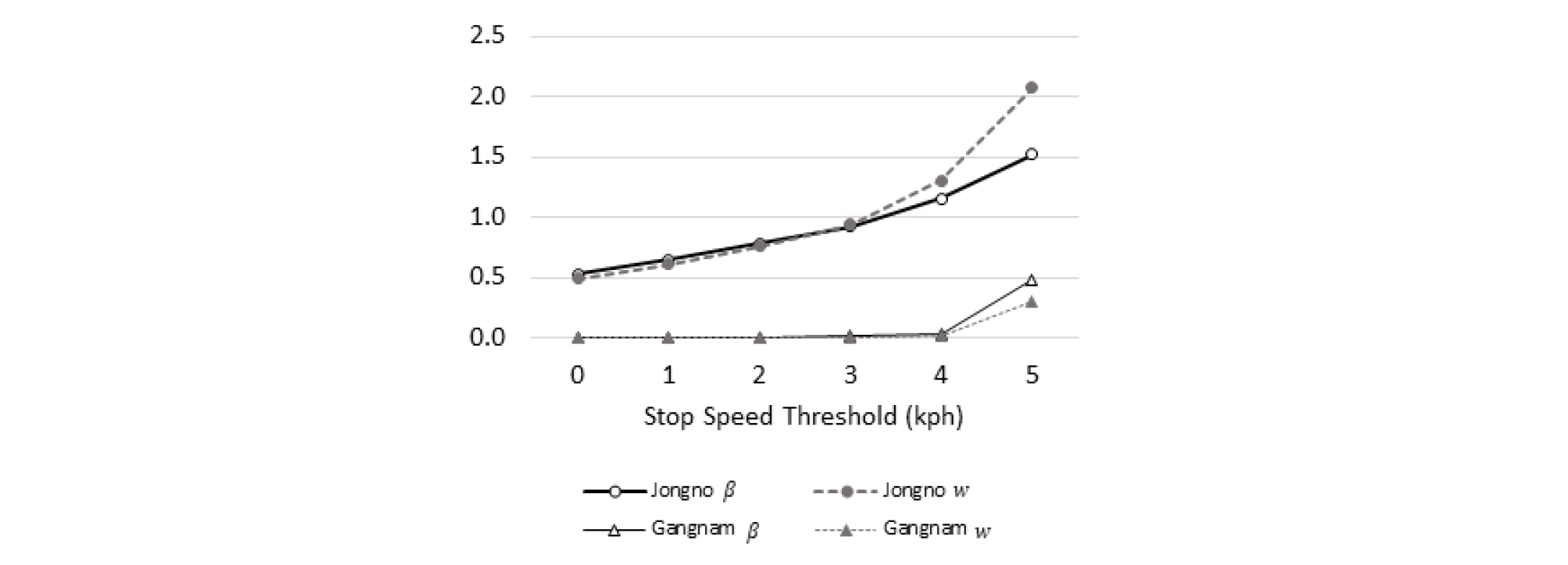
기존 연구들의 정지판단속도를 참고하여(Hong et al., 2003; Xiang et al., 2007; Dixit and Geroliminis, 2015; Pande et al., 2015; Lu et al., 2016; Lin et al., 2018; Lu et al., 2018) 본 연구는 정지판단속도를 0kph에서 5kph까지 변화시키면서 Perceived Crash Likelihood Factor (β)와 Crash Weighting Factor (w)의 민감도 분석을 수행하였다. Table 6을 보면, 종로 지역의 경우 정지판단속도 0kph에서 5kph까지 증가하는 동안 β는 3배가량, w는 4배 이상 증가하였다. 강남 지역의 경우 정지판단속도 0kph에서 4kph까지 β와 w가 거의 일정하였고, 5kph부터 두 값이 급증하였다.
Table 6. Sensitivity analysis of crash risk perception factors for stop speed threshold
결과적으로 Two-fluid Model 파라미터가 정지판단속도에 영향을 받는다는 기존 연구(Xiang et al., 2007)와 유사하게 교통사고 위험 인지 계수도 정지판단속도에 영향을 받는 것으로 나타났다. 이는 분석 시 설정한 정지판단속도에 따라 도로망 안전성의 결과 해석이 크게 바뀔 수 있음을 의미한다. 본 연구는 특정 지역에 대해서만 분석하였기 때문에 보편적으로 적용할 수 있는 정지판단속도를 제시하지는 않았다. 향후 신뢰성 있는 결과를 얻기 위한 정지판단속도를 결정하는 방법에 대한 연구가 필요할 것으로 판단된다. 또한, Figure 6에서 β와 w가 유사하게 변동하는 경향을 확인하였다. 이를 통해 두 계수 사이에 일정한 관계가 존재할 것으로 판단되며 이에 대한 추가적인 연구도 필요할 것으로 보인다.
결론
본 연구는 Dixit(2013)의 모형이 도시부 도로망의 안전성을 거시적으로 분석하는 데 활용될 수 있음을 실제 데이터를 통해 확인하고자 하였다. 이를 위해 택시 DTG 데이터를 이용하여 서울시 종로와 강남 지역의 교통사고 위험 인지 계수를 추정하였다. 차로 수가 많을수록 교통사고 발생확률이 높고, 교차로 밀도가 높을수록 교통사고 심각도가 높다는 기존 연구 결과와 종로 및 강남 지역을 비교한 본 연구 결과가 일관됨이 확인되었다.
GPS 데이터를 활용한 Two-fluid Model 분석 시 정지판단속도는 Two-fluid Model 파라미터 추정치에 영향을 미친다. 따라서 Two-fluid Model 파라미터를 활용하여 추정되는 교통사고 위험 인지 계수도 정지판단속도에 따라 영향을 받을 것으로 예상할 수 있었고, 이를 확인하기 위해 민감도 분석을 수행하였다. 그 결과, 정지판단속도가 증가함에 따라 두 계수가 증가하는 경향이 있었으며 두 계수의 변동이 거의 유사하였다.
본 연구는 Dixit(2013)이 제시한 모형의 도시부 도로망의 거시적인 안전성 분석에서의 활용 가능성을 실증 데이터를 통해 확인하였다. 향후 다양한 지역과 다양한 도로망 기하특성에 대한 분석을 통해 Dixit(2013)의 모형을 검증할 필요가 있으며, 교통사고 위험 인지 계수 간 관계를 밝히는 연구가 진행되어야 한다. 본 연구를 기초로 도시부 도로망의 거시적인 교통사고 위험도 연구가 가능할 것으로 기대된다.