서론
후미추돌 통합 위험도 모형 개발
1. 연구 수행 과정
2. 후미추돌 사고발생 확률
3. 심각한 상해발생 확률
실시간 후미추돌 통합사고위험도 평가 방법론 적용
1. 적용 대상 구간
2. 시뮬레이션 시나리오 설정
시나리오별 사고위험도 분석 결과
1. 교통사고 발생 전후 비교
2. 사고위험도 통합 평가 결과
결론 및 향후 연구과제
서론
도로를 이용하는 모든 차량들은 차량추종 및 차로변경 등의 주행패턴을 통해 끊임없이 상호작용을 한다. 교통안전 측면에서 각 차량들의 상호작용을 파악하여 사고 발생을 예측하고 더 나아가 탑승자의 상해를 추정하는 것은 교통 운영 전략을 설계하고 평가하는데 중요한 요소로 활용될 수 있다. 이에 효과적인 도로교통 운영을 위하여 개별차량 및 교통류의 위험 정도를 정량적으로 판단할 수 있는 기준 및 모형 개발에 관한 연구가 활발히 수행되었다(Essa and Sayed, 2018; Jo et al., 2019; Johnsson et al., 2018; Mahmud et al., 2017; Zheng and Sayed, 2019). 교통사고 발생 개연성을 계량화하여 나타낼 수 있는 교통안전 대체평가 지표인 Surrogate Safety Measure (SSM)이 개발되었으며, 대표적으로 Time-to-collision (TTC), Post-encroachment Time (PET), Deceleration Rate to Avoid Crash (DRAC)이 있다(Allen et al., 1978; Cooper and Ferguson, 1976; Hayward, 1971). 교통안전 평가지표와 관련하여 루프검지기에서 수집된 자료를 이용한 연구가 진행되었으며(Hossain and Muromachi, 2013; Oh et al., 2006; Pande and Abdel-Aty, 2006; Xu et al., 2013), 최근에는 차량의 주행궤적자료를 수집할 수 있는 기술이 가능함에 따라 개별차량 주행궤적 기반의 사고위험도 추정에 대한 연구가 활발히 진행되었다(Chatterjee and Davis, 2016; Oh and Kim, 2010; Przybyla et al., 2015; Xu et al., 2012). Wang et al.(2019)은 차량의 주행궤적 자료를 이용하여 Time-to-accident (TA), minimum Time-to-collision (mTTC), Maximum Deceleration rate (MaxD) 지표를 도출하였으며, 이를 활용하여 충돌확률 및 충돌빈도를 예측하는 이변량 모델을 제안하였다. 또한 개별 차량의 충돌 위험성을 평가하기 위하여 extended TTC를 이용한 연구가 수행되었으며, 교통량이 많은 혼잡상황에서 충돌 위험이 증가하는 것으로 나타났다(Xing et al., 2019).
사고발생 개연성을 고려한 안전성 평가뿐만 아니라 탑승자의 부상 심각도를 추정하는 연구도 수행되었다(Lubbe and Kiuchi, 2013; Nishimoto et al., 2017; Pérez et al., 2018). 사고 심각도를 나타내는 SSM으로 Delta-V가 있으며, 이는 실제 차량의 충돌이 발생했을 때 벡터속도변화를 나타내는 지표로 사고 충격량에 대한 추정이 가능하다(Gettman and Head, 2003). 사고 심각도 추정은 탑승자의 상해에 영향을 미치는 주요 요인인 Delta-V를 활용한 알고리즘 구축에 대한 연구가 수행되었다(Augenstein et al., 2006; Bahouth et al., 2012; Kononen et al., 2011). Laureshyn et al.(2017)은 승용차, 버스, 화물차로 차종을 구분하여 vehicle pair 간 상호작용을 분석하였으며, 상충 발생시 extended Delta-V가 높을수록 탑승자의 부상이 심각한 것으로 나타났다. 제안된 extended Delta-V는 두 차량의 사고발생 전후에 대한 속도차이에 중량을 반영한 지표로, 차종별 사고 심각도에 대해 비교 분석이 가능하다. 하지만, 다양한 차종별 중량분포를 고려한 탑승자의 상해 심각도 분석은 미비하였다.
최근에는 실시간으로 변화하는 도로 및 교통환경 그리고 운전자의 주행행태로 인해 불가피하게 발생하는 교통사고를 근본적으로 해결하기 위하여 도로, 차량, 관제센터를 연계한 통합 시스템의 필요성이 대두되고 있다. 또한 교통운영센터에서는 교통 정체를 유발하는 요인을 분석하고, 돌발상황 발생 시 사고대응 시간을 단축하여 사고심각도를 감소하고자 노력하고 있다. 이에 Cooperative-Intelligent Transport System (C-ITS)은 V2V (vehicle-to-vehicle) 및 V2I (vehicle-to-infrastructure) 통신을 기반으로 전방 돌발상황에 신속하게 대응할 수 있는 서비스를 제공할 수 있는 시스템으로, 도로와 차량 간의 통신에 기반을 두고 센터 중심의 소통정보를 제공해 왔던 기존 ITS와 차별화된다. C-ITS 차량은 Advanced Driver Assistance System (ADAS) 관련 전방충돌경고장치(Forward Collision Warning System, FCWS) 및 차로이탈경고장치(Lane Departure Warning System, LDWS) 서비스를 통해 전방차량과의 차간거리, 충돌예상시간에 대한 자료 수집이 가능하다. 또한, 주체차량과 선행차량의 주행속도, 가속도, 각속도, 브레이크 작동 및 세기와 같은 주행특성 자료에 대한 실시간 수집이 가능하다. C-ITS 및 ADAS 차량으로부터 실시간으로 수집되는 주행정보는 V2X 통신기술의 발달과 확산으로 빅데이터 처리가 요구된다. 빅데이터는 대용량 데이터를 다루는 특성상 한 대의 컴퓨터에 모든 데이터를 수집, 저장, 가공, 분석을 수행하는 것은 불가능하므로, 여러 대의 컴퓨터를 이용하는 분산 처리 기술이 요구된다. 즉, 빅데이터 분석 플랫폼 구축에 대한 연구가 선행되어야 하며 빅데이터를 효율적으로 처리하기 위한 하드웨어 및 소프트웨어 관련 문제가 기술적으로 해결되어야 할 것이다. C-ITS 및 ADAS와 같은 서비스 장착 차량은 선행차량에 대한 주행 빅데이터1)
수집을 통해 사고발생 개연성 및 상해 심각도를 고려한 통합사고위험도 평가가 가능할 것으로 판단된다. 따라서 본 연구의 목적은 실시간으로 개별차량의 후미추돌 사고 위험도를 계량화하여 통합 평가할 수 있는 지표를 개발하는 것이다. 후미추돌 발생 확률은 분석의 대상이 되는 주체차량을 중심으로 차로변경을 수행하지 않을 확률과 TTC확률을 결합하여 추정하였다. 심각한 상해 발생 확률은 후미추돌 개연성이 존재하는 차량에 대해 중량 및 속도에 대한 상해 심각도 모형을 도출하여 추정하였다. 본 연구의 결과물은 교통 운영자 및 관리자 입장에서 개별차량의 후미추돌 위험도를 예측함으로써 안전성 증대에 기여할 수 있다. 또한 통합 위험도가 높은 시간대를 식별하고 이를 관리하기 위한 다양한 대응책 개발 및 평가를 지원할 것으로 기대된다.
1) 주행 빅데이터: 빅데이터는 데이터의 규모, 수집, 종류, 복잡성 등의 측면에서 기존의 데이터와 구분되고, 분석 가능하지 않았던 새로운 인사이트(insight)를 도출할 수 있는 데이터를 의미함. 즉, 주행 빅데이터는 개별차량에 대한 주행정보를 포함하고 있는 빅데이터로 정의함.
본 연구의 구성은 다음과 같다. 2장에서는 후미추돌 사고발생 확률과 심각한 상해발생 확률을 추정하기 위한 방법론을 제시하였다. 3장에서는 시뮬레이션을 통해 사고 시나리오 구현에 관한 내용을 서술하였다. 4장에서는 시나리오별 통합 위험도 추정 결과를 제시하고, 5장에서는 본 연구의 활용방안에 대해 서술하였다. 마지막 장에서는 본 연구의 결과를 요약하고, 향후 연구과제에 대해 서술하였다.
후미추돌 통합 위험도 모형 개발
1. 연구 수행 과정
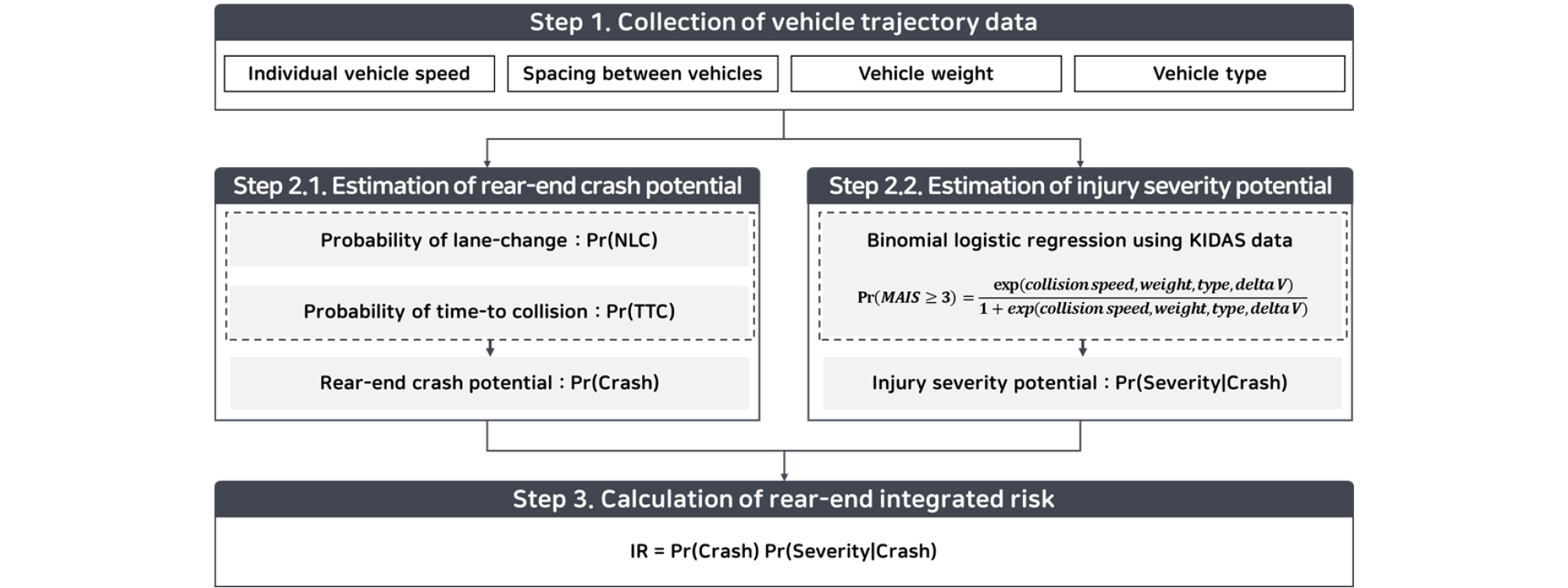
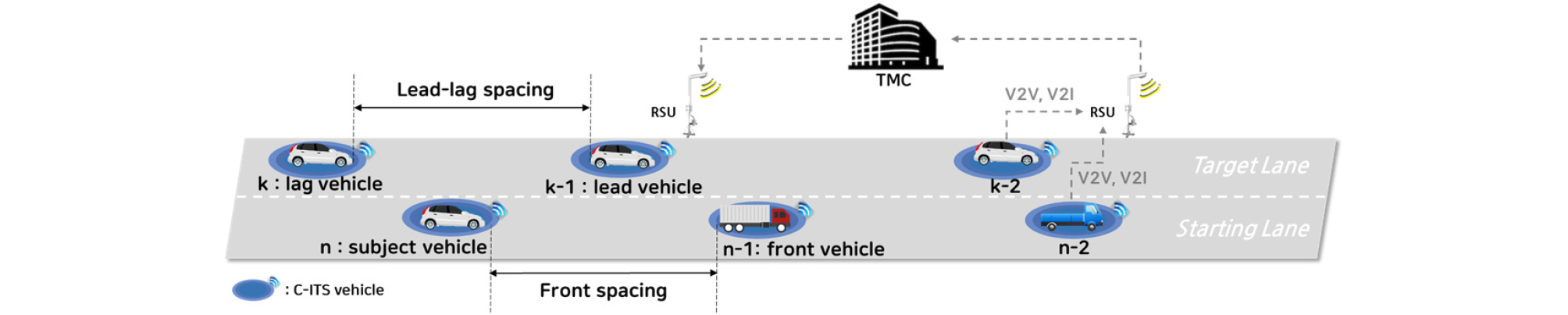
본 연구에서는 개별차량의 주행 빅데이터 수집 환경에서 후미추돌 사고발생 확률과 심각한 상해발생 확률을 추정하였다. 후미추돌 통합사고위험도 지표의 도출 절차를 Figure 1에 제시하였다. 첫째, 개별차량의 주행속도, 차량 간 spacing, 중량, 차종에 대한 자료를 매 시간 간격마다 실시간으로 수집한다. 수집된 자료 중 중량 및 차종에 대한 차량특성자료는 운전자가 입력한 정보를 V2V 통신을 통해 주고 받을 수 있다고 가정하였으며, 주체차량을 기준으로 상호작용 대상차량을 정의한다. 주체차량의 주행행태에 직접적으로 영향을 주고받는 상호작용 대상차량은 주행하는 차로의 전방차량과 인접한 차로의 전후방 차량으로 정의하였으며 Figure 2에 제시하였다. 주체차량과 전방차량 사이의 간격은 front spacing, 이웃한 차로를 주행하는 차량 사이의 간격은 lead-lag spacing이라 정의하였다. 둘째, 후미추돌 사고발생 확률과 심각한 상해발생 확률을 도출한다. 우선, 후미추돌 사고발생 확률은 주체차량과 선행차량이 차로변경을 수행하지 않을 확률과 TTC 확률을 결합하여 추정한다. 심각한 상해발생 확률은 KIDAS (Korean In-Death Accident Study Database) 자료를 이용하여 속도 및 중량에 대한 이항 로지스틱 회귀(Binomial Logistic Regression, BLR) 모형을 도출하여 추정한다. 모형의 종속변수는 MAIS (Maximum Abbreviated Injury Scale)로 설정하였으며, 탑승자의 부상 수준을 정량화하기 위해 정의된 척도로 3 이상을 기준으로 부상 심각도를 구분하였다.
마지막으로 조건부확률 및 확률의 곱셈법칙을 적용하여 후미추돌 사고발생 확률과 심각한 상해발생을 고려한 개별차량의 후미추돌 통합 위험도를 산출한다. 조건부 확률은 확률이 0이 아닌 사건 A에 대해 사건 A를 전제로 사건 B가 발생할 확률을 의미하며 Equation 1에 제시하였다. 본 연구에서는 후미추돌 사고발생을 전제로 심각한 상해가 발생할 확률을 나타낸다.
| $$\begin{array}{l}P(B\vert A)=\frac{P(A\cap B)}{P(A)}\\\Rightarrow P(severity\vert crash)=\frac{P(crash\cap severity)}{P(crash)}\end{array}$$ | (1) |
확률의 곱셈정리는 확률이 0이 아닌 두 사건 A, B에 대하여 P(A)와 조건부 확률 P(B|A)를 이용하여 을 산정할 수 있다. 따라서 후미추돌 발생 확률과 심각한 상해가 모두 발생할 확률은 Equation 2와 같으며 통합사고위험도를 나타낸다.
| $$P(crash\cap severity)=P(crash)P(severity\vert crash)$$ | (2) |
2. 후미추돌 사고발생 확률
Oh and Kim(2010)은 차량추적을 통한 개별차량의 주행 궤적자료는 미시적 교통류 분석을 통해 교통 상충의 잠재성 평가에 활용 될 수 있으며, 불안전한 미시적 교통상황을 식별할 수 있다고 제시하였다. 실시간으로 주체차량과 선행차량 간의 충돌 잠재성을 분석하는 것은 교통사고를 사전에 예측하고 효과적인 정보제공으로 교통 안전성을 향상시킬 수 있다. 개별차량의 후미추돌 사고발생 확률은 주체차량과 선행차량간의 추종상황에서 차로변경 하지 않을 확률과 TTC 확률을 결합하여 추정된다. 만약 주체차량 또는 선행차량이 차로변경을 수행할 경우 추종관계에서 벗어나 후미추돌 개연성이 사라지기 때문에 두 차량이 차로변경 하지 않을 확률을 산출해야한다. 또한 주체차량이 선행차량보다 속도가 높고, 현재 주행속도를 유지할 경우 TTC는 0에 가까워져 더 높은 충돌가능성을 가지게 된다. 반대로 선행차량이 주체차량보다 속도가 높을 경우 TTC는 무한히 증가하여 충돌 가능성은 거의 없게 된다. 따라서 주체차량과 선행차량의 차로변경과 두 차량 간의 상충이 독립적이라고 가정하면 후미추돌 사고발생 확률은 Equation 3과 같이 추정된다.
| $$Pr^{(t)}(crash_{n-1}^n)=Pr^{(t)}(NLC_n\vert X)\times Pr^{(t)}(NLC_{n-1}\vert X)\times Pr^{(t)}(C_{n-1}^n\vert TTC_{n-1}^n)$$ | (3) |
여기서, : 현재시점 t에서 subject vehicle (n)이 주어진 교통조건하에서 차로변경 하지 않을 확률
: 현재시점 t에서 front vehicle (n-1)이 주어진 교통조건하에서 차로변경 하지 않을 확률
: 현재시점 t에서 subject vehicle과 front vehicle이 주어진 TTC에서 충돌할 확률
차로변경 확률 모형은 BLR (Binomial Logistic Regression)을 적용하여 도출하였으며, BLR은 종속변수가 범주형으로 관측된 데이터를 적합 시킬 때 유용하게 사용되는 기법으로 ‘차로변경 수행 하지 않음 1’, ‘차로변경 수행함 0’으로 설정하였다. 차로변경 확률 모형은 운전자가 현재 주행 중인 차로와 이웃한 차로 중에서 이용 가능한 target lane을 계속적으로 평가한다는 것을 전제로 한다. 이때 주체차량 및 선행차량의 차로변경은 target lane이 좌측인 경우를 고려하였으며, 편도 2차로 이상의 고속도로의 경우 1차로는 앞지르기 차로로 구분되기 때문이다. 주변차량의 위치와 속도는 운전자의 차로변경 결정에 영향을 미치며 주체차량이 차로변경을 하지 않을 확률 모형은 Equation 4에 제시하였다.
| $$Pr(NLC_n\vert X)=\frac{exp(-0.045V_{n-1}-0.083V_k-0.046S_n^{n-1}+0.023S_k^{k-1}+11.475)}{1+exp(-0.045V_{n-1}-0.083V_k-0.046S_n^{n-1}+0.023S_k^{k-1}+11.475)}$$ | (4) |
여기서, : Front vehicle의 속도
: Lag vehicle의 속도
: Subject vehicle과 front vehicle의 차간거리
: Lag vehicle과 lead vehicle의 차간거리
주체차량이 차로변경 하지 않는 상황에 영향을 미치는 독립변수는 front vehicle과 lag vehicle의 속도, subject vehicle과 front vehicle 간의 차간거리, 그리고 lag vehicle과 lead vehicle의 차간거리가 선정되었다. 이는 선행차량의 속도가 느리고 주체차량과 선행차량간의 차간거리가 좁을수록 주체차량이 차로변경을 수행할 개연성이 높아지는 것을 의미한다. 또한, lag vehicle의 속도가 느리고 lag vehicle과 lead vehicle의 차간거리가 길수록 차로변경을 수행할 확률이 높아지는 것을 의미한다. 한편, TTC 확률 모형은 exponential decay function을 적용하였으며, 충돌 잠재성의 범위를 고려하여 a=0, b=1로 설정하였다. TTC 확률 모형은 Equation 5에 제시하였다.
| $$\begin{array}{l}y=a+b\times exp(-\frac zc)\\Pr^{(t)}(C_{n-1}^n\vert TTC_{n-1}^n)=exp(-\frac1c(\frac{S_n^{n-1}(t)}{V_n(t)-V_{n-1}(t)}))\end{array}$$ | (5) |
여기서, : 현재시점 t에서 subject vehicle의 속도
: 현재시점 t에서 front vehicle의 속도
: 현재시점 t에서 subject vehicle과 front vehicle의 차간 거리
: 곡률결정계수
따라서 후미추돌 사고발생 개연성은 주체차량과 선행차량의 차로변경 확률과 TTC 확률이 독립적이라고 가정할 경우, Equation 3은 Equation 6로 나타낼 수 있다.
3. 심각한 상해발생 확률
본 연구에서는 후미추돌 사고발생 시 탑승자의 심각한 상해발생 확률 모형을 구축하기 위하여 KIDAS (Korean In-Death Accident Study Database) 자료를 이용하여 BLR에 적용하였다. KIDAS는 한국형 자동차사고 심층조사 분석 자료로 사고차량에 관한 정보, 탑승자의 인적사항, 충돌속도 등을 제시하고 있다. 충돌로 인한 탑승자의 부상 수준을 정량화하기 위해 정의된 척도로 AIS (Abbreviated Injury Scale)을 사용하고 있으며 Table 1에 제시하였다.
Table 1. Definition of abbreviated injury scale
| AIS level | Definition |
| 1 | Minor |
| 2 | Moderate |
| 3 | Serious but not life threatening |
| 4 | Severe, Life threatening, Survival probable |
| 5 | Critical, Survival uncertain |
| 6 | Virtually unsurvivable |
심각한 상해발생 확률 모형의 종속변수는 탑승자의 AIS 최대값(Maximum AIS, MAIS) 3 이상을 기준으로 하여 ‘심각한 부상 1’, ‘경미한 부상 0’으로 설정하였다(Augenstein et al., 2006; Bahouth et al., 2012; Kononen et al., 2011). 탑승자의 상해에 영향을 미치는 독립변수는 충돌속도, 중량, 차종, Delta-V로 설정하였다. 2014년 6월부터 2016년 8월까지 의료기관의 사고 조사 자료와 사고재현 분석 자료에 대해 557 cases가 수집되었으며, 이 중 사고발생 지점이 고속도로인 88 cases를 분석에 적용하였다. 통계 프로그램인 IBM SPSS version 24를 이용하여 BLR을 수행한 결과를 Table 2에 제시하였다.
Table 2. Result of regression coefficient influencing severe injury
모형의 Chi-square 값은 3.014로 나타났으며 Nagelkerke 값은 0.768로 모델의 설명력이 우수한 것으로 나타났다. 탑승자의 상해에 영향을 미치는 변수는 충돌속도, 중량, Delta-V가 유의한 것으로 도출되었으며(p<0.05), 양의 상관관계가 있는 것으로 나타났다. 다시 말해서, 충돌속도, 중량, Delta-V가 증가할수록 탑승자의 상해가 심각할 개연성이 높아지는 것을 의미한다. BLR에 따른 심각한 상해발생 확률 모형은 Equation 7과 같다.
| $$Pr(severity\vert crash)=\frac{exp(0.091X_{cs}+0.002X_{weight}+0.110X_{delV}-11.027)}{1+exp(0.091X_{cs}+0.002X_{weight}+0.110X_{delV}-11.027)}$$ | (7) |
여기서, : 충돌속도
: 중량
: Delta-V
실시간 후미추돌 통합사고위험도 평가 방법론 적용
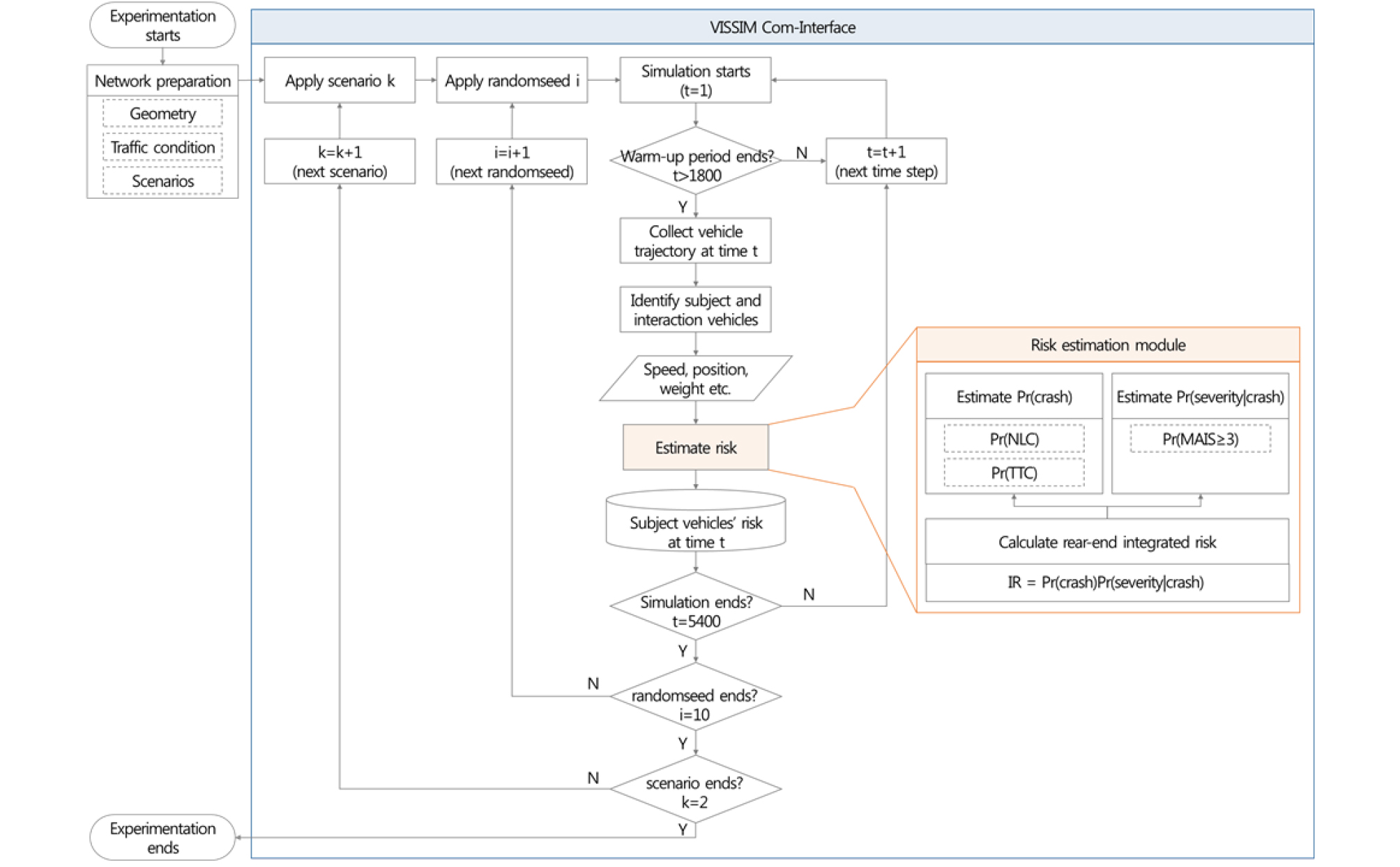
개별차량의 후미추돌 통합 위험도를 산출하기 위한 시뮬레이션 분석과정은 Figure 3과 같다. 미시교통류시뮬레이션 프로그램인 VISSIM을 이용하여 네트워크 환경을 구현하고, 분석 시나리오를 설정한 후 VISSIM COM-Interface를 활용하여 후미추돌 통합사고위험도를 산출한다. 시뮬레이션 시간은 총 5,400초로 warm-up time 1,800초를 제외하면 분석시간은 3,600초이며, warm-up time은 분석 네트워크에 교통량이 고르게 분포된 이후에 분석을 수행하기 위하여 설정하였다. 시뮬레이션 수행 시 동일 시나리오는 random seed를 다르게 적용하여 10번 반복 수행하였으며, 시뮬레이션 결과의 신뢰도를 높이기 위함이다.
1. 적용 대상 구간
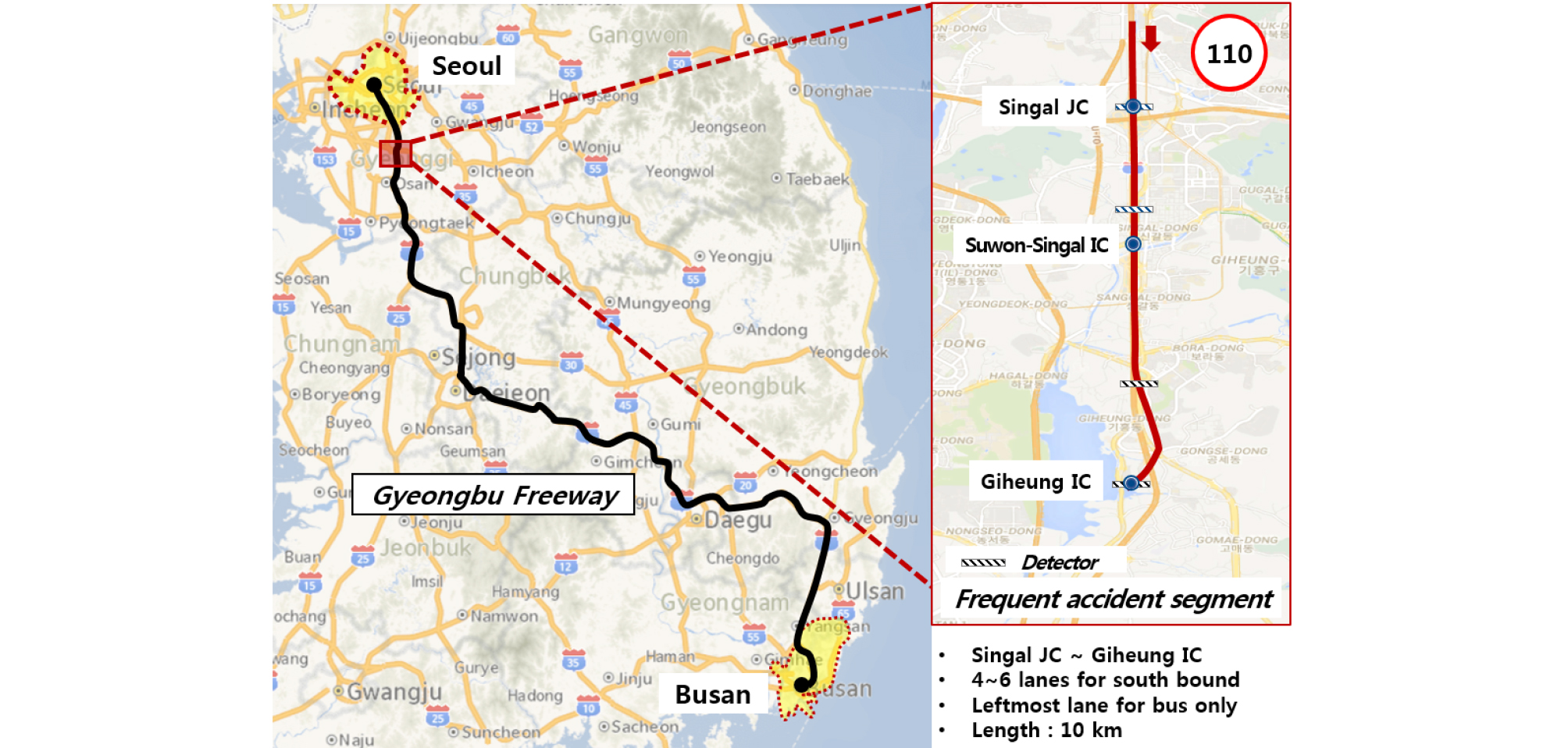
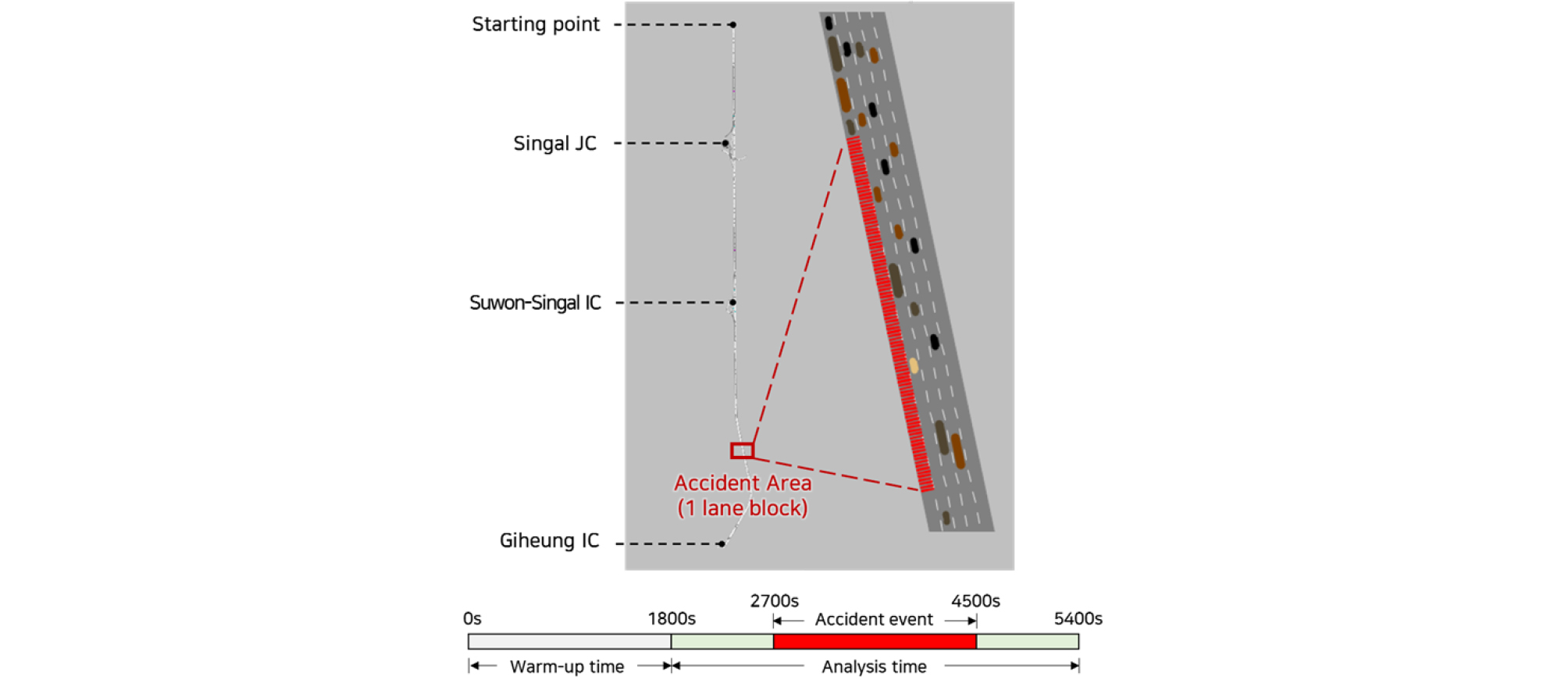
본 연구에서 개발한 방법론의 적정성 평가를 위해 VISSIM 7.0을 이용하였으며, Figure 4에 제시한 경부고속도로 신갈JC-기흥IC 부근의 10km 구간을 분석대상 구간으로 설정하였다. 해당 구간은 C-ITS 실증사업 구간 중 사고다발 구간이며, 2곳의 IC와 1곳의 JC를 포함한다. 본 구간은 편도 4-6차로이며 최 좌측차로인 1차로는 버스전용차로로 버스 통행만 허용된다. 추가적으로, 본 구간의 제한속도는 110km/h, 용량은 약 2,200pcphpl이다. 시뮬레이션을 통해 구현된 분석 네트워크를 일정수준 이상으로 실제 교통흐름과 유사하도록 구현하기 위하여 정산을 수행하였다. 분석 대상 구간에 설치된 4개의 VDS 검지기에서 5분단위로 수집된 교통자료와 시뮬레이션에서 수집된 자료를 비교분석하여 검증을 수행하였다. 이때, 시뮬레이션에서 수집된 자료는 VDS 검지기와 동일한 위치에서 지점 검지하여 수집된 자료를 5분 단위로 집계하여 반영하였다. 시뮬레이션 상의 도로가 실제 도로와 유사하게 구현 되었는지 검증하기 위해 속도를 효과척도로 사용하는 U-Value를 활용하여 검증하였으며, Equation 8에 제시하였다. U-Value 값이 0에 가까울수록 실제 데이터와 시뮬레이션 데이터가 유사함을 의미하며, 일반적으로 0.1 이하의 값으로 도출될 경우 실제 데이터와 일치한다고 판단할 수 있다(Brockfeld et al., 2004). 시뮬레이션을 10회 반복하여 U-Value 평균을 도출한 결과는 Table 3에 제시하였으며, 정산 검증 결과 모두 0.1 이하로 나타났다. 이는 VISSIM 네트워크 상의 도로가 실제 도로를 반영하였다고 판단할 수 있다.
| $$U=\frac{\sqrt{\sum_{i=1}^N(V_i-\widehat{V_i})^2}}{\sqrt{\sum_{i=1}^NV_i^2}+\sqrt{\sum_{i=1}^N\widehat{V_i}^2}}$$ | (8) |
여기서, : Actual speed (km/h)
: Simulation speed (km/h)
Table 3. Comparison of u-values between field and simulation loop detector data
2. 시뮬레이션 시나리오 설정
1) 차종별 요소 설정
본 연구에서는 승용차, 버스, 소형화물차, 중형화물차, 대형화물차로 차종을 분류하였으며, VISSIM을 통해 차종 비율, 속도 분포, 중량 분포에 대한 파라미터를 반영하였다. 분석대상 구간의 교통량은 약 6,400대/시로, 이 중 승용차 4,608대/시(72%), 버스 832대/시(13%), 소형화물차 640대/시(10%), 중형화물차 256대/시(4%), 대형화물차 64대/시(1%)인 것으로 나타났다. 유출입 교통량은 분석대상 구간에 설치된 4개의 VDS 검지기에서 수집된 교통량과 비교하여 설정하였다. 신갈JC의 유입교통량과 유출교통량은 각각 600대/시, 640대/시로 나타났으며, 수원신갈IC의 경우는 1,800대/시, 320대/시로 관찰되었다. 또한 기흥IC의 유출교통량은 780대/시로 나타나 분석에 적용하였다. 한편, 시뮬레이션의 속도 분포(desired speed distribution)는 분석대상 구간의 VDS 속도자료를 정규화하여 누적정규분포 그래프를 작성한 후 반영하였다. VDS는 중량 측정이 불가능하기 때문에, 차종별 중량 분포(desired weight distribution)를 설정하기 위하여 고속도로 과적단속장비인 WIM (Weigh-In-Motion)의 중량 자료를 활용하였다. 본 연구에서는 경부고속도로에 설치된 WIM으로부터 수집된 차종별 중량자료를 정규화하여 누적정규분포 그래프를 도출함으로써 중량 분포에 대한 파라미터를 설정하였다. 본 연구에서 사용한 속도 및 중량 자료의 기초통계량은 Table 4에 제시하였다.
Table 4. Descriptive statistic of speed and weight
2) 사고 시나리오 설정
개별차량의 사고 개연성은 속도, 가속도, 차간간격과 같은 주행특성 자료에 대한 실시간 수집을 통해 추정 가능하다. 본 연구에서는 미시교통류시뮬레이션인 VISSIM을 통해 수집된 개별차량 주행궤적 자료를 분석에 활용하였다. 시뮬레이션을 통해 추정된 SSM은 높은 충돌 위험을 지닌 이벤트 및 차량을 검지할 수 있으나, 실제 사고 자료는 이를 포함하지 않는다. 따라서 사고 상황(crash case)과 일반 상황(non-crash case)에 대해 SSM을 비교 분석하는 과정이 필요하다(Cunto et al., 2009, Shi et al., 2018; Zhao and Lee, 2018). 본 연구에서는 수원신갈IC-기흥IC 사이 100m 구간에 대해 교통사고로 인한 차로 통제 상황을 구현하고, 후미추돌에 대한 통합사고위험도를 비교하였다. VISSIM의 신호기를 이용하여 사고구간의 시점과 종점사이에 red time을 부여함으로써 최 우측차로인 1개 차로를 통제하였다. 총 1시간의 분석시간 중 30분 동안 사고가 발생한 것으로 가정하였으며, 사고 시나리오에 대해 Figure 5에 제시하였다.
시나리오별 사고위험도 분석 결과
1. 교통사고 발생 전후 비교
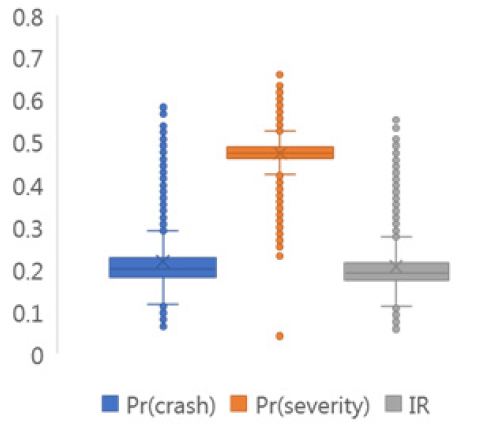
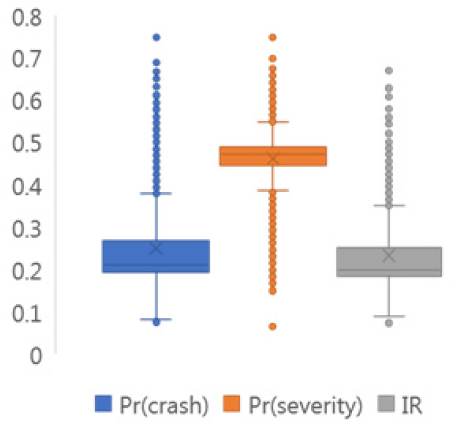
본 연구에서는 VISSIM을 이용하여 동일한 분석 네트워크에서 사고발생 유무에 대한 시뮬레이션을 수행하였다. 시나리오별 후미추돌 사고발생 확률, 심각한 상해발생 확률, 그리고 통합사고위험도에 대한 기초통계량을 Table 5에 제시하였다. 일반 상황보다 사고 상황에서 후미추돌 사고발생 확률이 높은 것으로 나타났으며, 이는 차로통제로 인한 강제적 차로변경이 요구되어 상충 개연성이 증가한 것으로 판단된다. 반면, 차로통제로 인한 정체가 발생하여 차량의 주행속도 및 차량 간 속도차이가 낮아 심각한 상해발생 확률이 감소한 것으로 분석되었다. 최종적으로 시나리오별 후미추돌 개연성 증가율이 상해 심각도 감소율보다 높은 것으로 나타나 통합사고위험도가 증가한 것으로 도출되었다. 일반 상황과 사고 상황에 대해 각 사고위험도 지표 간 통계적으로 차이가 존재하는지 검증하기 위하여 t-test를 수행하였다. 분석결과 각 사고위험도 지표는 95% 신뢰수준에서 통계적으로 유의한 차이(p<0.05)가 존재하는 것으로 나타났으며, Table 6에 제시하였다.
Table 5. Comparison of crash risks by scenarios
Table 6. Comparison of crash risks by t-test
2. 사고위험도 통합 평가 결과
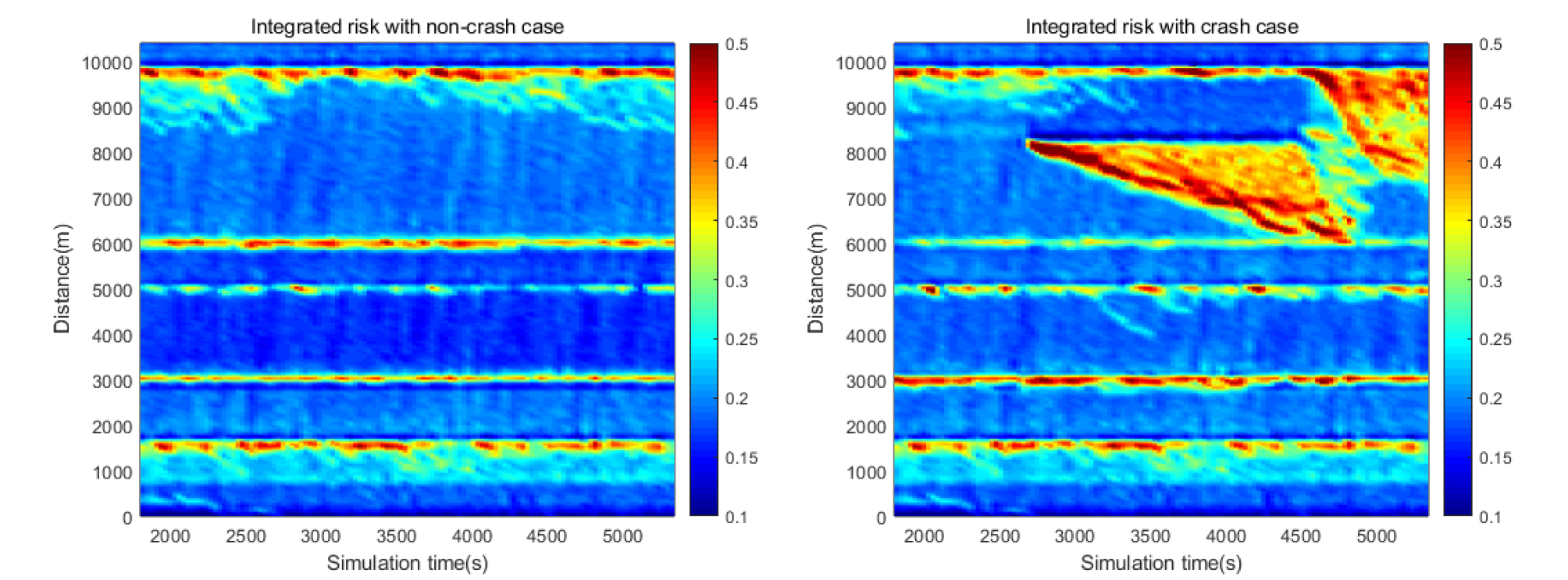
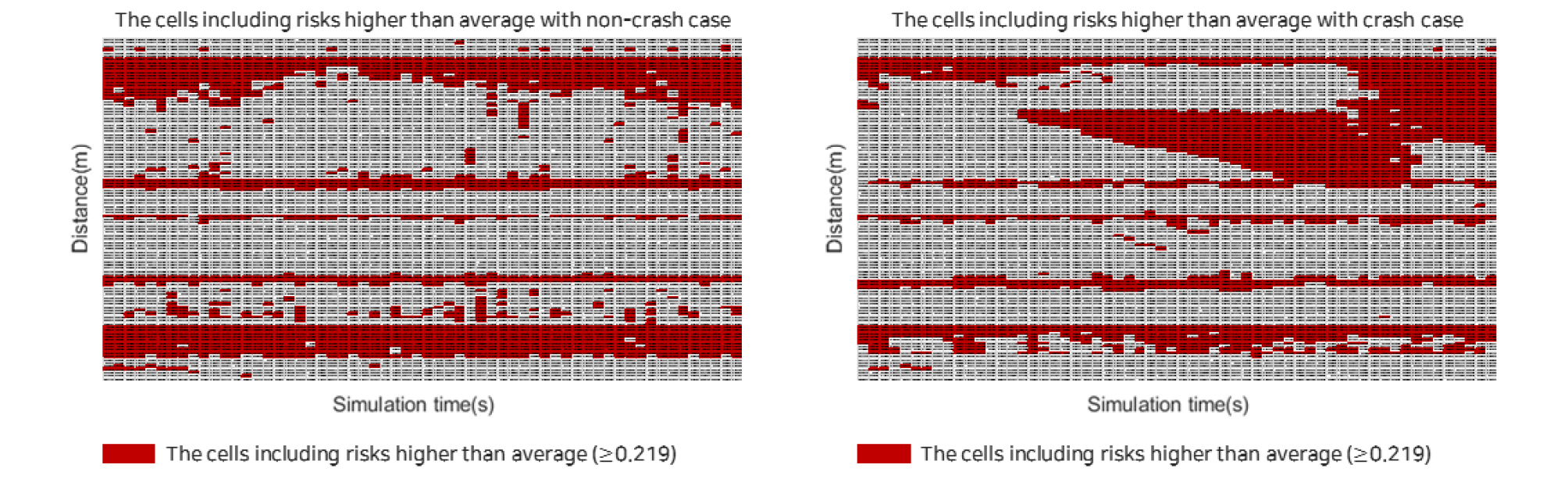
개별차량의 사고위험도는 시 ‧ 공간을 기반으로 셀 단위로 집계하였으며, 사고위험도가 높은 구간 및 시간대를 식별하기 위함이다. 따라서 분석구간 10km에 대해 100m 단위, 분석시간 3,600초에 대해 60초 단위로 구분하여 전체 셀의 개수는 6,000개로 설정하였다. 시나리오별 후미추돌에 대한 통합사고위험도 시공도는 Figure 6에 제시하였다. 유출입 연결로 부근에서 진출입 차량의 차로변경은 상충을 유발하고, 차량 간 상대적인 속도차이가 증가하기 때문에 고속도로 본선보다 유출입 연결로에서 통합사고위험도가 높은 것으로 나타났다. 특히, 사고 상황에서 사고발생 구간의 통합사고위험도가 증가하였으며, 사고발생 시간이 지날수록 상류부의 통합사고위험도가 높아지는 것으로 분석되었다. 사고발생 시간 이후에는 하류부의 통합사고위험도가 증가하는 것으로 나타났으며, 이는 차로통제로 인한 정체 및 대기행렬이 해소되면서 하류부의 교통량이 증가하고 밀도가 높아졌기 때문이다.
사고발생 시 통합사고위험도에 미치는 영향을 정량적으로 분석하기 위하여 Equation 9와 같이 시공도의 전체 셀의 개수 중 통합사고위험도 평균 값 이상의 셀의 비율을 산출하였다. 일반 상황과 사고 상황을 모두 고려한 통합사고위험도의 평균은 0.219로 나타났으며, 이를 초과한 셀의 개수는 일반 상황에서 1,463개, 사고 상황에서 2,176개로 도출되었다. 따라서 Risk rate는 일반 상황에서 24.4%, 사고 상황에서 36.3%로, 사고발생 시 통합사고위험도에 미치는 영향이 11.9% 더 높은 것으로 분석되었다. 시나리오별 평균 통합사고위험도를 초과하는 셀에 대해 Figure 7에 제시하였다.
| $$Risk\;Rate=\frac{AC}{TC}\times100(\%)$$ | (9) |
여기서, : The number of cells including risks higher than average
: The total number of cells ()
결론 및 향후 연구과제
V2V 및 V2I 통신을 기반으로 실시간으로 변화하는 도로 및 교통환경 그리고 운전자의 주행 빅데이터에 대한 수집이 가능함에 따라, 능동적이고 효과적인 교통사고 대응책 개발을 위한 SSM에 대한 연구가 지속적으로 수행되고 있다. 본 연구에서는 실시간으로 개별차량의 후미추돌 사고 위험도를 계량화하여 통합 평가할 수 있는 지표를 개발하였다. 조건부확률 및 확률의 곱셈법칙을 적용하여 후미추돌 사고발생 확률과 심각한 상해발생 확률을 고려한 개별차량의 통합사고위험도를 산출하였다. 본 연구의 분석방법론을 적용하기 위하여 VISSIM을 통해 네트워크 환경을 구현하고, 사고유무에 따른 시나리오에 대해 후미추돌 통합사고위험도를 산출하였다. 분석결과, 고속도로 본선보다 유출입 연결로에서 통합사고위험도가 높은 것으로 나타났으며, 특히 사고발생 시간이 지날수록 상류부의 통합사고위험도가 높아지는 것으로 분석되었다. 사고발생 시 통합사고위험도에 미치는 영향을 정량적으로 분석하기 위하여 Risk rate를 정의하였으며, 사고로 인한 차로통제 상황에서 통합사고위험도가 약 12% 증가하는 것으로 나타났다. 본 연구의 결과는 개별차량의 사고 개연성 및 상해심각도 추정을 통해 후미추돌 사고위험도의 통합 평가를 위한 지표 개발에 활용될 것으로 기대된다.
국내에서는 개별차량에게 전방 돌방상황에 대해 유용한 정보를 제공하여 교통안전을 제고하는 시스템으로 C-ITS 실증 사업이 수행되고 있다. C-ITS는 교통안전 관점에서 사고대응 및 심각도감소를 위하여 도로, 차량 등 교통의 구성요소에 통신기술을 적용하고, 교통정보를 수집, 관리, 제공함으로써 이용효율을 극대화하는 교통체계 시스템이다. 본 연구에서 제시한 통합사고위험도 추정 방법론은 사고발생 및 공사 구간 등 차로통제 상황에서 사고위험도를 줄이기 위한 정보제공에 활용될 수 있다. 예를 들어, 충격파 원리를 통해 사고위험도를 반영한 Risk Wave Theory를 제시하여 Risk Wave 속도 도출을 통한 경고정보 제공이 가능할 것으로 판단된다. 이는 사고위험도가 높은 구간의 상류부에 경고정보제공 및 가변속도제한 등 교통관리 기법 적용 시 적절한 서비스 제공 위치를 도출함으로써 통합사고위험도 감소를 기대할 수 있다.
본 연구에서는 주체차량을 중심으로 주변차량의 속도, 위치, 중량 정보 등을 수집하여 통합사고위험도를 추정하였으나, C-ITS 환경에서 도로를 주행하는 모든 차량의 주행정보 및 차량특성정보를 수집하는데 실질적으로 어려움이 존재한다. 이에 따라, C-ITS 및 ADAS 차량으로부터 수집되는 표본정보, 즉 자료수집 비율에 따라 사고위험도 추정을 위한 모형개발에 대한 연구가 수행되어야 할 것이다. 이는 일정 수준 이상의 주행정보 수집 비율이 분석대상 도로구간의 사고위험도를 나타낼 수 있는지 판단하기 위함이다. 또한, 주체차량과 선행차량의주행정보만으로 후미추돌 사고개연성 추정이 가능한 다양한 SSM에 대한 고려가 필요하다. 차량추종 상황에서 후행차량이 위험상황을 인지하고 감속하기 시작할 때의 충돌 회피 감속도를 나타내는 DRAC을 이용하여 CPI 도출이 가능하고, 선행 ‧ 후행 차량의 최소 정지거리 차이를 나타내는 SDI (Stopping Distance Index) 등 안전성 평가가 가능하다. 주행 빅데이터에 대한 표본정보를 활용하여 여러 SSM 도출을 통해 사고개연성을 추정하는데 우수한 성능을 나타내는 모형개발에 대한 연구가 지속적으로 수행되어야 할 것이다.
본 연구에서 제시한 개별차량의 사고위험도 통합 평가에 대한 신뢰도를 높이기 위해서는 다음과 같은 추가적인 연구가 필요하다. 첫째, C-ITS 및 ADAS 시스템 장착 차량으로부터 수집된 주행정보를 이용하여 개별차량의 사고위험도를 분석할 필요가 있다. 본 연구에서는 시뮬레이션을 통해 고속도로 특정 구간에 대해 분석을 수행하였으나, 연속류 및 단속류를 대상으로 연구의 범위를 확장할 경우 사고위험도가 높은 구간 및 시간대 식별이 가능할 것으로 판단된다. 둘째, KIDAS 자료에 대한 추가적인 수집을 통해 보다 신뢰성 있는 모형 구축이 필요하다. 본 연구에서는 차량의 주행속도, 중량, Delta-V를 이용하여 심각한 상해 확률 모형을 도출하였으나, 운전자 및 차량 특성에 대한 변수를 추가적으로 고려할 필요가 있다. 마지막으로, C-ITS 및 ADAS 차량 비율에 따른 다양한 시나리오를 설정하고, 일반차량과 서비스 장착 차량의 운전자 반응행태 및 차량 거동을 고려하여 사고위험도 비교분석이 수행되어야 한다. C-ITS 및 ADAS 차량은 전방 교통사고, 장애물 정보 등 각종 유용한 서비스를 제공받기 때문에 일반차량보다 인지반응시간이 길고, 급격한 속도변화가 적은 특성을 고려한 주행 파라미터가 반영되어야 할 것이다.
빅데이터는 데이터의 규모, 수집, 종류, 복잡성 등의 측면에서 기존의 데이터와는 구분되고, 분석 가능하지 않았던 새로운 인사이트(insight)를 도출할 수 있는 데이터를 의미한다. 본 연구에서 주행 빅데이터는 개별차량에 대한 주행정보를 포함하는 빅데이터로 정의하였다. 본 연구의 결과는 주행 빅데이터를 이용하여 개별차량의 안전성 평가뿐만 아니라 사고 위험도가 높은 구간 및 시간대를 식별하는데 의의가 있다. 앞서 언급한 향후 연구내용에 대한 체계적인 분석을 통해 실질적으로 적용 가능한 결과 도출을 위한 다각적인 노력이 필요할 것이다.