서론
기존 연구
방법론
1. 부스팅 기계학습 알고리즘
2. 평가 기준값 산출
데이터
1. 데이터 수집
2. 데이터 집계
노면 온도 특성 분석
1. 지형, 시설물에 따른 노면 온도 변화
2. 블랙아이스 발생 조건 분석
블랙아이스 예측 모형 구축
1. 입력 데이터
2. 모형 구축
모형 평가
결론 및 향후 연구
서론
최근 블랙아이스로 인한 교통사고가 사회적 이슈이다. 2019년 상주영천고속도로에서 블랙아이스 교통사고가 발생해 7명이 사망하고 42명이 다쳤다. 유사한 사고가 2023년 구리포천고속도로에서도 발생해 1명이 숨지고 3명이 다쳤다. 2024년 1월 3일에도 세종시에서 블랙아이스 교통사고가 발생해 차량 28대가 파손되고 14명의 부상자가 발생했다. 도로교통공단 통계에 따르면 최근 5년간 서리․결빙으로 인한 교통사고는 총 4,392건 발생했고, 그로 인한 사망자는 122명에 달했다(KoROAD, 2023). 미국에서도 노면 미끄럼으로 인해 연평균 562,182건의 교통사고가 발생했고, 그로 인해 1,705명의 사망자, 138,735명의 부상자가 발생했다(FHWA, 2023). 스웨덴의 한 연구보고서에 따르면 미끄러운 노면에서 약 14%의 운전자만이 올바른 가․감속을 하고, 약 50%의 운전자는 미끄러운 노면을 정상 노면으로 오인식하는 것으로 분석되었다(Bogren et al., 2010). 포루투갈의 한 연구에 따르면 미끄러운 노면에서 교통사고 발생 확률이 마른 노면 대비 최대 10배까지 증가한다고 하였다(Luque et al., 2013).
이러한 블랙아이스 교통사고 예방을 위해 국토교통부는 “도로제설업무 수행요령” 개정을 통해 제설대책기간(11월 13일-3월 15일) 야간 취약 시간대(23-7시) 도로 순찰을 의무화 하였다. 도로 순찰 중 블랙아이스를 발견하면 제설제를 살포하여 블랙아이스 교통사고를 예방한다. 하지만 일반국도의 경우 도로 연장이 약 14,000km로 길고 순찰 차량은 약 17대로 제한되어 있어 전체 구간을 순찰하는 것이 현실적으로 불가능하다. 만약 블랙아이스 발생 가능성이 높은 구간을 사전에 알 수 있다면 해당 구간을 집중적으로 순찰할 수 있어 겨울철 도로관리 업무 효율성을 높일 수 있다. 하지만 일반국도에는 도로기상 관측망이 구축되어 있지 않아 블랙아이스 발생 위험도 정보가 없는 실정이다. 이에 본 연구에서는 기상청에서 발표하는 기상 데이터를 이용하여 블랙아이스 발생 위험 구간을 추정하는 방법을 제안하고자 한다. 온도, 습도, 풍속, 강수 확률 등 기상청 예보는 최소 6시간 이전에 발표되기 때문에 기상 데이터를 이용하면 블랙아이스 위험 구간을 사전에 파악할 수 있다.
추정 방법론은 2009-2018년에 걸쳐 개발된 3가지 부스팅(AdaBoost, XGBoost, CatBoost) 알고리즘을 이용했다. 부스팅 기법은 앙상블(ensemble) 모형의 하나로 기계학습 시 오류 데이터에 더 많은 가중치를 두어 학습하기 때문에 분류 성능이 우수해 많은 분야에 활용되고 있으나(Abdullah et al., 2024), 블랙아이스 추정 방법으로는 적용된 사례가 없다. 알고리즘 평가를 위한 블랙아이스 기준값은 순찰 차량이 수집한 야간 노면 온도 데이터를 이용했다. 노면 온도가 영하이고 이슬점 온도보다 낮은 경우, 물리법칙에 의거, 블랙아이스가 발생한 것으로 간주했다. 이슬점 온도는 Magnus 공식을 이용해 산출했다. 순찰 차량 수집 노면 온도 데이터를 이용해 블랙아이스가 발생하는 조건도 분석했다. 마지막으로 부스팅 기법을 이용해 구축한 블랙아이스 추정 모형별 성능 비교 및 장ㆍ단점 분석을 수행했다.
기존 연구
블랙아이스 발생 조건은 크게 3가지로 나누어진다. 녹은 눈이 재결빙되는 경우, 어는 비가 내리는 경우, 서리ㆍ안개가 발생하는 경우이다. 눈, 비가 내리는 경우는 운전자가 상대적으로 쉽게 인지할 수 있으나, 서리ㆍ안개에 의해 발생하는 블랙아이스는 운전자가 인지하기 어렵다. 2024년 1월 3일 세종시에서 발생한 블랙아이스 사고도 새벽에 발생한 서리ㆍ안개에 의해 발생했다. 따라서 본 연구에서 구축한 블랙아이스 추정 모형은 안개ㆍ서리에 의해 발생하는 블랙아이스에 초점을 두었다.
미국 등 선진국을 중심으로 널리 활용되고 있는 블랙아이스 예측 모형은 물리 모형과 회귀 모형으로 분류된다. 물리 모형은 포장 층의 열교환 매커니즘을 이용하여 노면 상태를 예측한다. 태양 복사에너지를 기반으로 지중과 포장 층의 열 전도‧대류 현상을 물리 모형으로 만들어 노면 온도를 추정하고 이를 이용해 블랙아이스 정보를 생산한다(PIARC, 2018; Louis et al., 2001; Tina et al., 2006; Claudia et al., 2016). 회귀 모형은 기상, 도로 기하구조 등 데이터를 이용하여 노면 온도를 예측한 후 블랙아이스 정보를 추정한다(Virve, 2019; Lee et al., 2001; Veronica et al., 2010).
국내에서도 노면 결빙과 관련한 몇몇 연구가 이루어졌다. Kim et al.(2022)은 결빙 도로에서 발생하는 교통사고를 예측하는 딥러닝 기반의 모형을 개발해 서울시 데이터를 이용해 검증했다. Lee et al.(2019)은 기상 데이터와 노면 상태 정보를 이용하여 노면의 습윤 상태를 예측하는 랜덤 포레스트 기반의 모형을 제안했다. Son et al.(2018)은 에너지수지법을 이용해 강우 시 노면의 수분 증발량을 산정하여 노면의 습윤 상태를 추정하는 방법론을 개발했다.
그러나 기존 모형은 다음과 같은 한계가 있다. 물리 모형은 포장 층의 열전도율, 태양 복사 에너지, 지중 온도 등 다양한 파라미터가 필요하다. 포장 층의 열전도율은 포장 재료, 공법 등에 따라 다양하게 나타나고, 태양 복사에너지와 지중 온도는 도로기상 관측장비가 설치되어야 획득할 수 있다. 하지만 본 연구 대상 도로인 일반국도에는 도로기상 관측장비가 설치되지 않아 이러한 파라미터 획득이 불가능하다. 회귀 모형은 단순하여 이해가 쉬우나 일반적으로 비선형성을 나타내는 기상정보 예측에 적용하기에는 정확도 측면에서 불리한 것으로 알려져 있다(Mats et al., 2012). 국내에서도 노면 상태를 예측하는 몇몇 연구가 있었으나, 본 연구에서와 같이 전국적으로 수집한 야간 노면 온도 데이터를 이용하여 노면 상태 예측 방법론을 제시한 사례는 없는 것으로 파악된다.
따라서 본 연구는 머신러닝 기법 중 하나인 부스팅 알고리즘을 이용해 블랙아이스를 추정하는 알고리즘을 개발하였다. 이러한 머신러닝 기반의 블랙아이스 추정은 최근 들어 몇몇 연구가 진행되고 있지만, 아직 초기 단계 기술개발에 머물러 있다(Yumei et al., 2019; Lee et al., 2022; Lake, 2023). 본 연구에서 적용에서 적용한 부스팅 기법은 블랙아이스 추정에 적용된 사례가 없다. 부스팅 머신러닝 알고리즘은 학습 시 오류를 나타내는 데이터에 가중치를 부여하는 방식으로 진행하기 때문에 본 연구와 같이 수집된 자료가 제한적인 경우, 타 머신러닝 알고리즘에 비해 우수한 성능을 나타내는 것으로 알려져 있다(Khan et al., 2021). 전술했듯이 본 연구 대상이 일반국도는 도로기상 관측장비가 설치되어 있지 않아, 기상청에서 예보하는 기상 데이터를 이용하여 블랙아이스를 추정하는 모형을 개발했다. 기상청 오픈 API를 통해 쉽게 획득할 수 있는 데이터를 사용했기 때문에 입력 데이터 수는 많지 않으나, 개발 알고리즘의 활용성은 우수할 것으로 판단된다.
방법론
1. 부스팅 기계학습 알고리즘
부스팅 기계학습 알고리즘은 앙상블 모델의 한 종류로서 이는 가중치를 활용하여 약 분류기(weak learner)를 강 분류기로 만드는 방법이다. Figure 1과 같이 전체 학습 데이터 셋을 다수의 소규모 학습 데이터 셋으로 분류할 때 이전 데이터 셋에서 오류로 판정한 데이터를 다시 하위 데이터 셋에 포함시키는 방법으로 학습이 진행된다. 본 연구에서는 대표적인 부스팅 알고리즘인 AdaBoost, XGBoost, CatBoost 모형을 이용하여 블랙아이스 예측 모형을 구축했다.
AdaBoost(Adaptive Boost)는 Zhu et al.(2009)이 제안한 모형으로 초기 약한 모형(weak learner) 생성 후 단계마다 가중치를 이용해 이전 모형의 약점을 보완한다. 이 경우 가중치는 이전 모형에서 오류를 발생시킨 데이터에 더 높게 부여하는데, 이는 부스팅 모형의 일반적인 특성으로 이전 모형이 예측하지 못한 데이터에 더 집중하여 결과적으로 전체 데이터를 더 잘 예측하는 모형을 생성한다. 이렇게 새로운 모형을 순차적으로 적합한 뒤 마지막으로 다수 모형의 선형 결합을 통해 최적 모형을 구축한다.
XGBoost(Extreme Gradient Boost)는 Chen et al.(2016)이 개발한 모형으로 기존 Gradient Boosting 알고리즘 단점인 과적합 문제를 개선한 모형이다. 과적합 방지를 위해 XGBoost 알고리즘에는 새로운 파라미터(λ, γ)가 추가되었다. XGBoost는 기본 학습기(base learner)를 의사결정나무로 하고 잔차를 이용하여 이전 모형을 개선하면서 최적 모형을 생성한다. 이러한 XGBoost 모형은 데이터 수가 충분히 많은 경우 양호한 성능을 발휘하지만 학습 데이터 수가 적은 경우 과적합 문제를 해결할 수 없는 단점이 있다.
CatBoost(Categorical Boost)는 Dorogush et al.(2018)이 제안한 방법론으로 특히 분류 목적에 특화된 부스팅 알고리즘이다. 타 부스팅 모델과 달리 CatBoost는 학습 데이터 일부에 대해 잔차를 계산한 후 그 결과를 이용해 모형을 다시 만드는 방식으로 작동한다. 학습 데이터 일부를 선택할 때 일정한 순서를 가지고 선택하기 때문에 “Ordered Boosting” 방법으로도 불린다. 다시 말해, 학습 데이터 샘플링 시 임의의 순열을 만들어 순차적으로 잔차를 계산하면서 학습하기 때문에 “Target Leakage”를 최소화한다. 이를 통해 기존 Gradient 부스팅 알고리즘의 단점인 과적합 문제를 해결한다. 또한 CatBoost는 시계열 데이터를 효율적으로 처리하고 타 부스팅 모형에 비해 처리 속도가 빨라(XGBoost 대비 8배) 낮은 하드웨어 사양으로도 많은 데이터를 처리할 수 있는 장점이 있다(Hancock et al., 2020).
2. 평가 기준값 산출
블랙아이스 추정 모형 평가를 위해서는 실제로 블랙아이스가 발생했는가에 대한 기준값이 필요하다. 가장 좋은 방법은 블랙아이스를 직접적으로 측정하는 장비를 이용하여 수집하는 것이나, 이는 장비, 인력 등 측면에서 많은 비용이 소요된다. 따라서 본 연구에서는 일반국도 순찰 차량이 수집하는 야간 노면 온도 데이터와 물리법칙을 이용하여 평가 기준값을 산출했다. Equation 1과 같이 블랙아이스는 노면 온도가 영하이고 이슬점 온도보다 낮을 때 발생한다.
여기서, Tp = 노면 온도, Td = 이슬점 온도
여기서 노면 온도는 순찰 차량 데이터를 이용하면 되지만 이슬점 온도는 직접 측정할 수 없어 적정한 계산식을 이용해 산출해야 한다. 이슬점이란 공기 중 수증기가 포화해 응결이 일어나는 온도이다. 본 연구에서는 이슬점 온도를 계산하기 위해 기상학 분야에서 일반적으로 널리 사용되는 Magnus 공식을 이용했다. 주어진 온도 조건(T)에서 포화 수증기압은 Magnus 공식에 의해 Equation 2와 같이 나타낼 수 있다.
Equation 2에서 파라미터 값은 기존 연구에 의해 α = 6.112ha, β = 17.62, λ = 243.12℃로 결정되었다(Sonntag, 1990). Equation 2를 이슬점 온도를 산출하기 위해 재정리하면 Equation 3과 같이 표현된다.
Equation 3을 상대 습도 정의(E = RH*EW/100)를 이용해 재정리하면 Equation 4와 같이 기온과 상대 습도를 이용하여 이슬점 온도를 산출하는 식으로 표현할 수 있다.
Equations 2,3,4에서 표현한 Magnus 공식은 공기 중의 기온과 상대 습도 데이터를 이용하여 이슬점 온도를 계산할 때 주로 이용되고 있으며, 계산된 이슬점 온도 오차는 0.35℃로 알려져 있다(Lawrence, 2005). Magnus 공식에 의해 산출된 이슬점 온도와 순찰 차량을 이용해 수집한 노면 온도 데이터를 이용해 Equation 1과 같이 산출한 블랙아이스 기준값 검증을 위해 현장 조사를 수행했다. 그 결과, Figure 2와 같이 블랙아이스 조건을 만족한 경우<좌>와 만족하지 않는 경우<우>가 확연한 차이가 있었다. 블랙아이스 조건을 만족한 경우<좌>는 서리에 의해 발생한 블랙아이스로 인해 노면이 미끄러운 것을 확인했다.
데이터
1. 데이터 수집
일반국도에서는 겨울철 블랙아이스 예방을 위해 매일 취약 시간대(23-7시) 순찰 차량이 일정 구간을 순찰하면서 노면 온도 데이터를 수집한다. 구간별 데이터 수집 시각은 서버로 전송되지 않아 정확한 시각은 파악이 불가능하다. 본 연구는 이러한 도로 순찰 차량이 수집한 노면 온도 데이터를 이용했다. 순찰 차량에 Figure 3과 같이 부착된 노면 온도 센서는 적외선 방식으로 노면 온도를 측정한다. 기상측기 전문 교정기관 검정 결과, 센서 측정 오차는 ±0.3℃로 나타나 정확도가 양호했다. 노면 온도는 초당 5회 측정되어 국토부 도로제설관리시스템으로 실시간 전송된다. 노면 온도에 대응하는 기상 데이터는 순찰 차량이 통과하는 시점의 기상청 동네예보를 통해 수집하였다. 데이터 수집 구간은 Figure 4에서 녹색 선으로 표시한 일반국도 구간(약 1,000km)이며 데이터 수집 기간은 2개 시즌(2021년 12월-2022년 3월, 2022년 12월-2023년 3월)이었다.
현재는 블랙아이스 예측 모형이 없어 매일 일정 구간을 순찰하면서 노면 온도를 측정하고 블랙아이스가 발견되거나 예상되면 제설제를 살포하는 방식으로 겨울철 도로관리를 수행하고 있다. 만약 블랙아이스를 사전에 예측할 수 있다면 블랙아이스 발생이 예상되는 날에만 순찰하면 되기 때문에 현재에 비해 효율적으로 겨울철 도로관리를 수행할 수 있을 것이다. 이에 본 연구는 기상청에서 예보하는 동네예보 데이터를 이용하여 야간 블랙아이스를 추정하는 모형을 개발하였다.
2. 데이터 집계
전술했듯이 순찰 차량이 수집하는 노면 온도는 초당 5회 수집되어 차량의 GPS 좌표, 수집 시각과 함께 서버로 전송된다. 이러한 고해상도의 노면 온도 데이터를 개별적으로 표시하는 것보다 일정 구간 단위로 집계하는 것이 유리하다. 이를 위해 본 연구에서는 국토교통부 표준링크 데이터를 활용했다. 표준링크는 교량, 터널, 지하차도 등 도로 구조물 특성별로 분리되어 있기 때문에 블랙아이스 추정을 위한 공간적 집계 단위로 적정하다. 일반적으로 노면 온도는 도로 시설물 특성별로 다르게 나타난다고 알려져 있다(Gustavsson, 1990).
일반적으로 순찰 차량을 이용해 수집한 노면 온도 데이터는 노면 이물질, 갓길 정차 등 다양한 요인에 의해 간헐적으로 이상치(outlier)가 수집되는 것으로 알려져 있다(Shao et al., 1995). 따라서 Song et al.(2012)은 순찰 차량 수집 노면 온도 데이터를 공간적으로 집계할 때 이상치에 의해 발생할 수 있는 부정적 영향을 최소화해야 한다고 하였다. 이에 본 연구에서는 개별 노면 온도 데이터를 표준링크 단위로 집계할 때 해당 링크 수집 노면 온도 값을 단순 평균하기보다는 이상치에 의한 영향이 상대적으로 적은 중간값을 사용했다(ASTM, 2008).
노면 온도 특성 분석
1. 지형, 시설물에 따른 노면 온도 변화
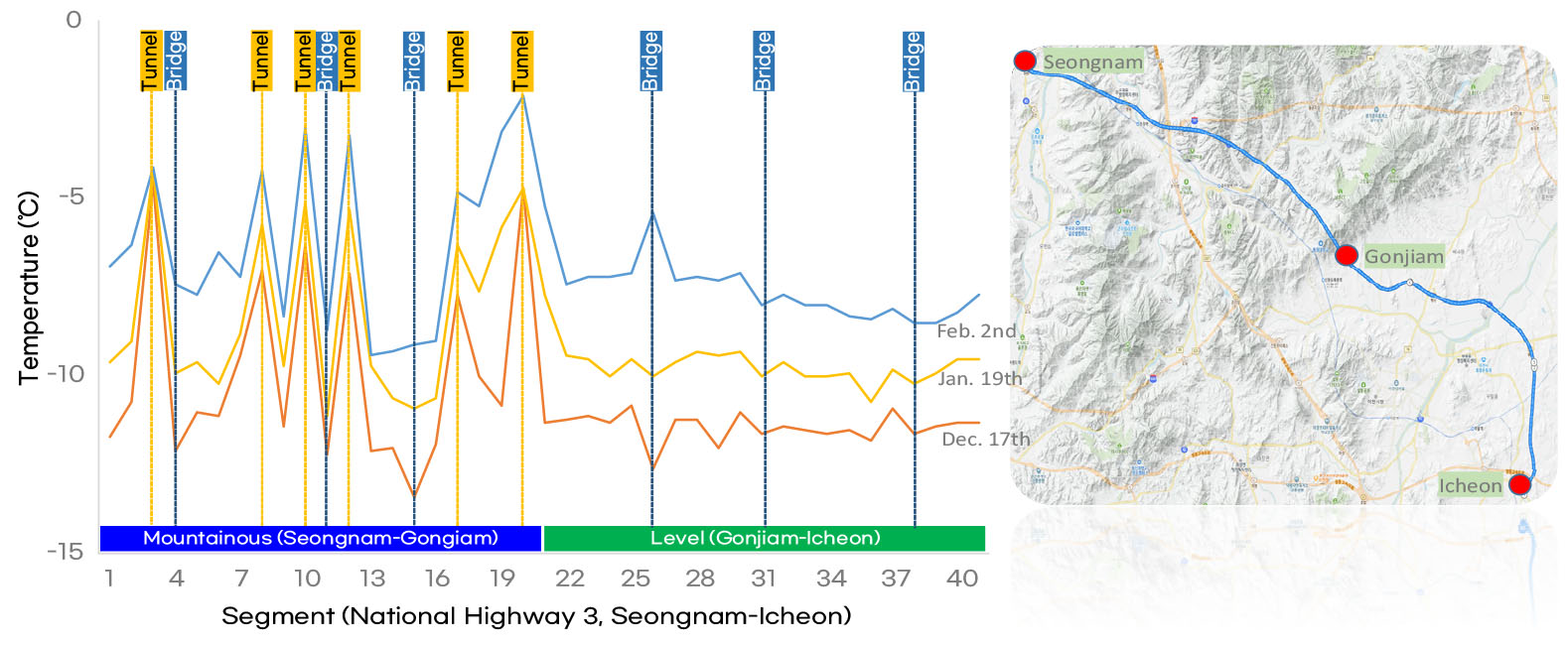
일반적으로 노면 온도는 주변 지형 및 시설물 유형에 따라 달라진다고 알려져 있다(Gustavsson, 1990). 순찰 차량이 수집한 노면 온도를 지형, 시설물 유형에 따라 분석하기 위해 국도 3호선(성남-이천, 약 50km) 노면 온도 데이터를 Figure 5와 같이 개별 구간으로 매칭했다. 데이터 수집 시기는 2023년 12월 17일, 2024년 1월 19일, 2024년 2월 2일 취약 시간대(23-7시)였다.
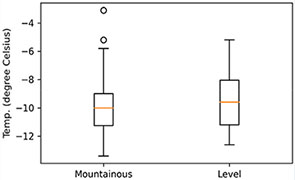
Table 1은 지형에 따른 노면 온도 분포, Table 2는 시설물 유형에 따른 노면 온도 분포를 보여준다. 유의할 점은 지형에 따른 노면 온도 통계량에는 동일 조건 유지를 위해 터널 데이터를 포함하지 않았다. 지형 분류는 Figure 5 위성 사진을 기반으로 정성적으로 구분했다. 분석 결과, 산악 지형이 평지 지형보다 노면 온도가 낮고(평균 0.4℃), 편차가 큰 것으로 나타났다. 교량은 일반 도로 구간보다 노면 온도가 낮게(평균 0.8℃) 관측되는 것으로 나타났고, 터널은 높게(평균 4.3℃) 나타났다.
Table 1.
Pavement temperature by terrain
| Statistics | Mountainous | Level |
| Mean | -9.9℃ | -9.5℃ |
| Std. dev. | 2.0℃ | 1.7℃ |
| Min. | -13.4℃ | -12.6℃ |
| 25% | -11.3℃ | -11.2℃ |
| 50% | -10.0℃ | -9.6℃ |
| 75% | -9.0℃ | -8.1℃ |
| Max. | -3.1℃ | -5.2℃ |
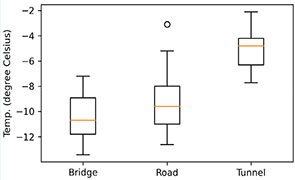 | ||
Table 2.
Pavement temperature by facility type
| Statistics | Bridge | Road | Tunnel |
| Mean | -10.2℃ | -9.4℃ | -5.1℃ |
| Std. dev. | 1.8℃ | 1.9℃ | 1.4℃ |
| Min. | -13.4℃ | -12.6℃ | -7.7℃ |
| 25% | -11.8℃ | -11.0℃ | -6.3℃ |
| 50% | -10.7℃ | -9.6℃ | -4.8℃ |
| 75% | -8.9℃ | -8.0℃ | -4.2℃ |
| Max. | -7.2℃ | -3.1℃ | -2.1℃ |
 | |||
2. 블랙아이스 발생 조건 분석
전술했듯이 블랙아이스는 노면 온도가 영하이고 이슬점 온도보다 낮을 때 발생한다. 본 연구에서는 순찰 차량 수집 노면 온도 데이터를 이용해 블랙아이스 발생 시 기온과 상대 습도 패턴을 분석했다. 추풍령 부근 국도 4호선 데이터(2023년 1월 22일-3월 15일) 분석 결과, 블랙아이스가 발생하는 일수는 Figure 6과 같이 4일(붉은색 세로선)로 나타났다.
여기서 유의할 점은 비나 눈이 내리는 경우는 분석에서 제외했다. 눈ㆍ비가 내리는 경우 노면 온도가 영하이면 결빙이 발생하기 때문에 Equations 1,2,3,4와 같은 복잡한 분석을 할 필요가 없다. 실제로 국토교통부 제설 매뉴얼(MOLIT, 2023)에 따르면 겨울철 눈ㆍ비가 내리고 기온이 4℃ 이하일 경우 제설 작업을 수행하기 때문에 강수 시에는 별도의 예측 정보가 필요 없고, 단지 기상청이 발표하는 기상정보만을 활용하면 된다.
Figure 6에서 보듯이 블랙아이스가 발생하는 날의 기상은 기온이 4℃ 이하이고 상대 습도가 75% 이상이었다. 다시 말해 기온이 4℃보다 높고 상대 습도가 75%보다 낮은 날에는 눈이 내리지 않는 경우 블랙아이스가 발생하지 않는다는 의미이다. 또 하나 흥미로운 점은 기온이 내려가는 시기보다 기온이 내려간 후 올라가는 시기에 블랙아이스가 주로 발생한다는 것이다. 이는 기온이 상승하는 경우 대기 중의 수증기가 증가해 상대 습도가 높아지기 때문인 것으로 보인다.
이상의 분석 결과에서 알 수 있듯이 1월 22일-3월 15일간 단 5일만 블랙아이스 발생 조건을 충족했음에도 매일 도로 순찰을 실시했다. 이는 겨울철 도로관리 효율성 저하, 제설제 과다살포 등 문제점을 야기할 수 있다. 따라서 본 연구에서는 기상청에서 예보하는 기상 데이터를 이용하여 야간 블랙아이스를 추정하는 방법론을 제시했다. 자세한 내용은 다음 장에서 다루고자 한다.
블랙아이스 예측 모형 구축
1. 입력 데이터
이상의 분석 결과를 바탕으로 기상청에서 발표하는 기상 예보 데이터를 이용하여 야간 블랙아이스를 추정하는 모형을 개발했다. 모형 입력 데이터는 블랙아이스 취약 시간대(23-07시) 1시간 단위로 발표하는 기온, 상대 습도, 강수 확률, 풍속, 이슬점 온도이다. 이 중 이슬점 온도는 Magnus 공식을 이용해 계산하였다. 강수 확률 데이터는 일사량(태양 복사에너지) 대용으로 강수 확률이 높은 경우 일사량이 낮아져 노면 온도가 낮아질 수 있다. 데이터는 2022-2023년 2개 시즌 데이터를 사용했다.
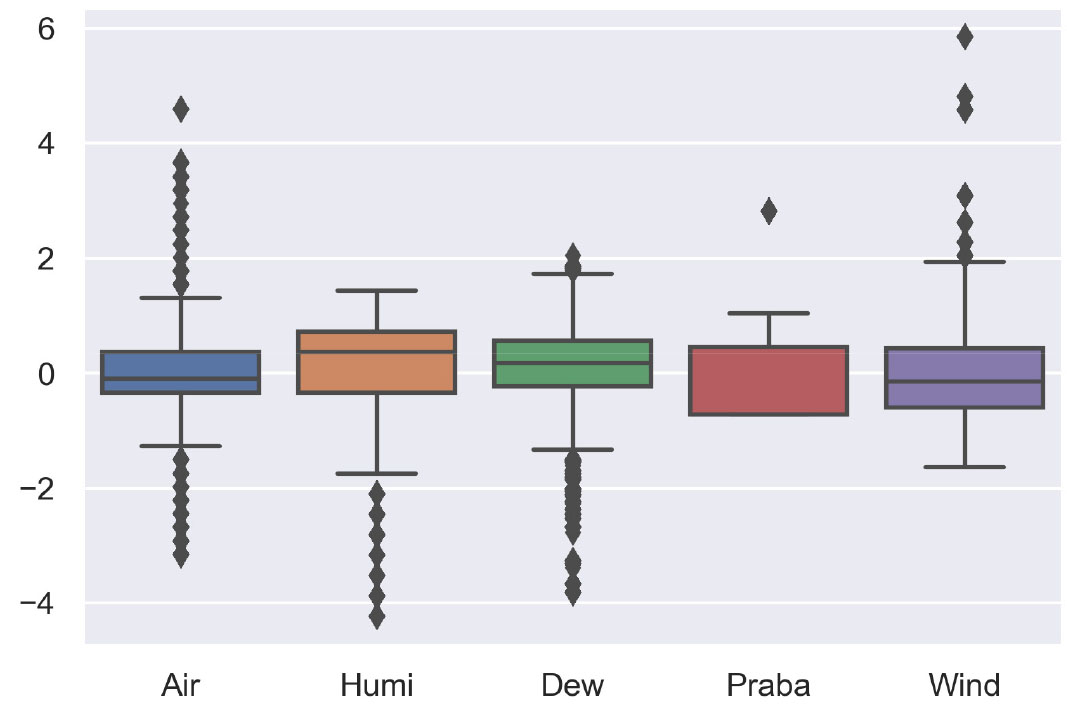
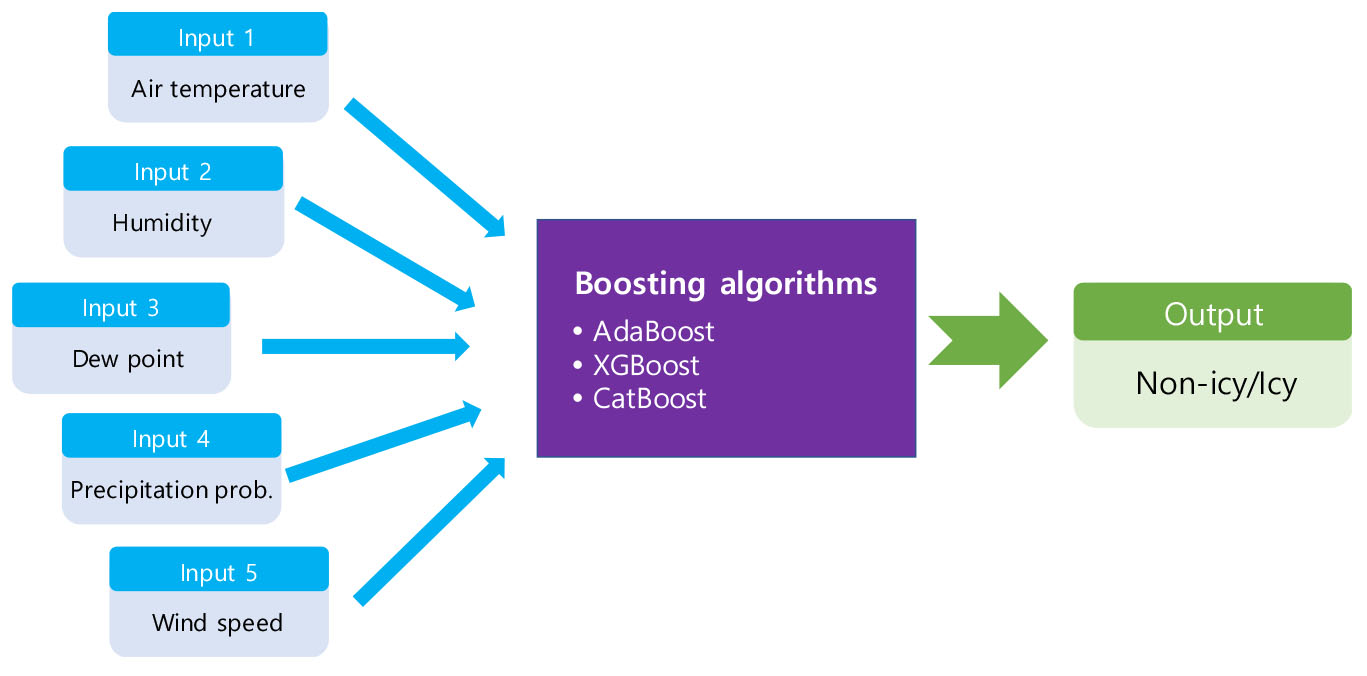
블랙아이스 추정 모형은 일반적으로 널리 활용되는 3가지 부스팅 알고리즘(AdaBoost, XGBoost, CatBoost)을 이용해 구축되었다. Figure 7은 정규화된 입력 데이터의 상자 그림을 보여준다. 상대 습도, 이슬점 온도는 음의 방향으로, 풍속은 양의 방향으로 조금 치우쳐 있으나 전체적으로 0을 중심으로 정규화된 분포를 나타내어 머신러닝 입력값으로 적절한 것으로 판단된다. Figure 8은 부스팅 모형 구축 개요도를 보여준다. 모형 구축 시 훈련과 테스트 데이터는 7:3의 비율로 나누었고 훈련과 테스트 데이터 셋에 블랙아이스 발생과 미발생 데이터는 균등 배분하였다. 모형 구축에 사용된 총 데이터는 20,870개이고 이 중 블랙아이스 발생 데이터는 9,313개, 블랙아이스 미발생 데이터는 11,558건이다.
2. 모형 구축
AdaBoost 알고리즘은 추정기 수(number of estimator)와 학습률(learning rate) 파라미터 설정이 필요하다. 이를 위해 모형 구축 시 격자 탐색(grid search) 알고리즘을 이용했다. 격자 탐색 알고리즘은 주어진 모든 파라미터 조합을 대상으로 모형을 학습하고 평가하여 가장 우수한 성능을 나타내는 파라미터 조합을 찾아내는 기계학습 방법이다. 탐색 파라미터 범위 및 최적 파라미터 조합은 Table 3과 같았다. AdaBoost 모형에서 입력 변수 중요도(0-1)는 Figure 9과 같이 이슬점 온도가 가장 높고 풍속과 기온이 그 뒤를 이었다.
Table 3.
Optimal parameters for AdaBoost model
| Parameter | Optimal | Parameter grid |
| n_estimators | 4000 | [2000, 3000, 4000, 5000] |
| learning_rate | 0.1 | [0.001, 0.01, 0.1] |
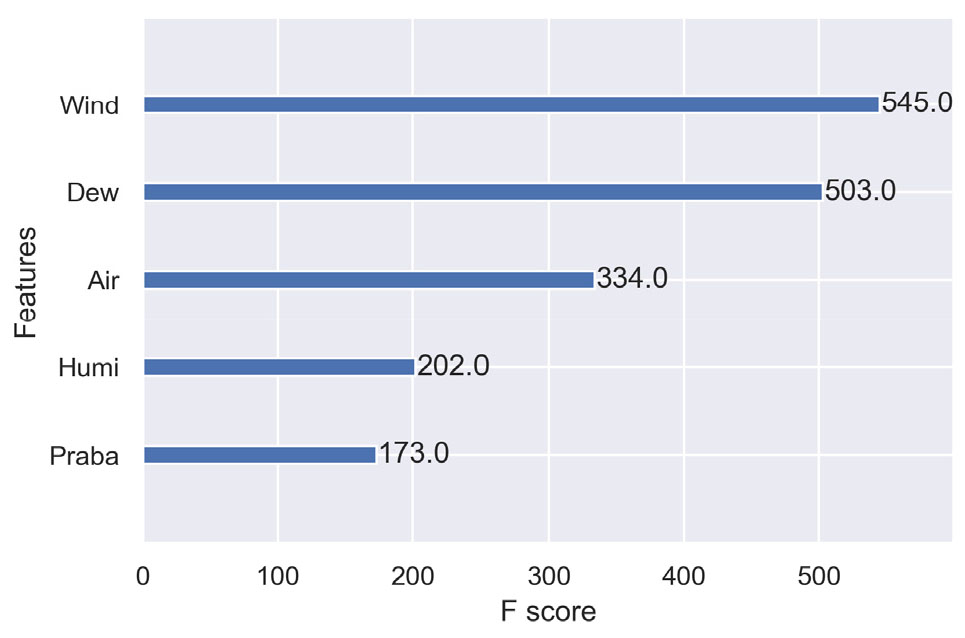
Figure 10는 본 연구에서 구축한 XGBoost 모형 학습 과정을 보여준다. 테스트 데이터 셋을 이용하여 모형을 테스트한 결과, 부스팅 수가 40회 이상일 경우 오차(log loss) 감소 효과가 크지 않은 것을 알 수 있다. Figure 11은 각 입력 변수에 대한 중요도(F 점수)를 나타낸다. XGBoost 알고리즘에서는 풍속이 가장 높은 중요도를 보였고 이슬점 온도, 기온이 그 뒤를 따랐다.
Figure 12는 본 연구에서 구축한 CatBoost 모형 학습 과정을 보여준다. 테스트 셋 데이터를 이용하여 정확도(F1 score)를 계산한 결과, 반복 횟수가 70회 이상일 때 일정한 값을 나타냈다. 반복 횟수가 30회까지는 성능이 급격히 상승하지만 40회 이후부터는 성능 향상 폭이 크지 않은 것을 알 수 있다. 입력 변수 중요도를 계산한 결과, Figure 13와 같이 상대 습도가 가장 큰 중요도를 보였고 풍속과 이슬점 온도가 그 뒤를 이었다. 이상에서 살펴본 바와 같이 적용 알고리즘(AdaBoost, XGBoost, CatBoost)에 따라 입력 변수 중요도가 다르게 작용하는 것을 알 수 있었다.
모형 평가
Table 4는 3가지 모형에 대한 성능을 보여준다. 성능은 Equations 5,6,7과 같이 기계학습 분야에 널리 사용하는 평가 척도인 정밀도(Precision), 재현율(Recall), F1 점수(F1 Score)를 사용했다. 정밀도는 분류 모형이 Positive(Icy)로 판정한 것 중 실제로 Positive인 표본 수 비율이고, 재현율은 실제 Positive 표본 중 분류 모형이 Positive로 판정한 비율이며, F1 점수는 정밀도와 재현율의 조화평균이다. 평가 결과, AdaBoost 알고리즘을 제외하고 모두 약 90% 수준의 성능을 보였다. AdaBoost 알고리즘의 경우 낮은 성능에도 불구하고 모형 구축 시 소요 시간 타 알고리즘에 비해 약 5배 이상 소요되어, 모형의 적합성과 효율성 측면에서 불리한 결과를 보였다. Table 5는 3가지 모형에 의한 테스트 데이터 셋 분류 결과를 보여준다. AdaBoost 알고리즘은 결빙이 발생하지 않은 구간을 결빙으로 판정하는 오류가 높게 나타났다.
Table 4.
Comparison of model performance
| Model | Precision | Recall | F1 Score |
| AdaBoost | 0.80 | 0.87 | 0.85 |
| XGBoost | 0.89 | 0.90 | 0.91 |
| CatBoost | 0.88 | 0.91 | 0.90 |
Table 5.
Confusion matrix of constructed models
3가지 모형 평가 결과, 기상 데이터를 이용한 블랙아이스 추정은 XGBoost와 CatBoost 모형이 성능, 처리 시간 측면에서 적합한 것으로 나타났다. 변수 중요도는 각 변수가 분류(split)될 때 불순도(impurity) 감소분의 평균이 높은 순서대로 정해지는 것으로 XGBoost는 풍속, CatBoost는 습도가 가장 중요한 변수로 작용했다. 이는 기계학습 알고리즘 특성에 기인하는 것으로 개별 알고리즘 적용 시 데이터 확보 우선순위 선정 시 활용될 수 있을 것으로 사료된다.
여기서 유의할 점은 본 평가에 사용된 기준값은 전술했듯이 노면 상태 실측값이 아니고 노면 온도와 이슬점 온도를 이용한 계산값이다. 물론 물리법칙에 의거 기준값 산출 방식이 합리적인 것으로 판단되지만, 블랙아이스 발생 조건이 충족되더라도 야간 차량 통행이 많은 경우 타이어-노면 마찰열 등으로 실제로는 블랙아이스가 발생하지 않을 수도 있다. 그럼에도 불구하고 본 연구 결과는 운전자 및 도로 관리자 측면에서 다음과 같은 중요한 의의를 갖는다. 운전자 측면에서는 실제 블랙아이스가 발생하지 않더라도 야간에 전방 시야가 제한적인 상황에서 블랙아이스 발생 조건이 충족될 경우 블랙아이스 정보를 제공하여 감속, 차간 거리 확보 등을 유도할 수 있다. 도로 관리자 측면에서는 블랙아이스 발생 조건이 충족하는 경우 제설제를 사전 살포하는 등 방법으로 예방적 도로관리를 수행할 수 있어 겨울철 도로 안전성 향상 측면에서 큰 효과가 있다.
결론 및 향후 연구
최근 해마다 반복되는 블랙아이스 교통사고로 인해 겨울철 도로 안전이 사회적 이슈로 부각되고 있다. 2019년 상주영천고속도로 블랙아이스 사고 이전의 우리나라 겨울철 도로관리는 눈이 내릴 때 신속하게 눈을 치우는 것이 주목표였다. 하지만 최근에는 기후변화 등의 영향으로 겨울에도 비가 내리는 경우가 잦고, 안개‧서리에 의한 블랙아이스 발생 빈도도 높아지고 있다. 이러한 문제에 대응하기 위해 최근 고속도로에는 도로기상 관측망이 설치되고 있고, 실시간 노면 상태 정보도 제공되고 있다. 하지만 예산 문제로 국도, 지방도에는 도로기상 관측망 구축 계획이 없다. 이에 본 연구에서는 도로기상 관측망이 구축되지 않은 도로를 대상으로 기상 예보 데이터(기온, 상대 습도, 이슬점 온도, 강수 확률, 풍속)를 이용해 블랙아이스를 추정하는 모형을 개발했다.
개발 모형 평가를 위해 국도 순찰 차량이 2개 겨울 시즌 동안 전국 약 1,000km 구간에서 수집한 노면 온도 데이터와 Magnus 공식에 의해 산출한 이슬점 온도 데이터를 이용해 기준값을 획득했다. 노면 온도 데이터 분석 결과, 블랙아이스는 기온이 4℃ 이하이고, 상대 습도가 75% 이하일 때만 발생하는 것으로 나타났다. 이는 기온이 4℃라도 노면 온도는 영하가 될 수 있음을 의미하고, 상대 습도가 75% 이상일 때 안개ㆍ서리가 발생함을 알 수 있다. 또 한 가지 흥미로운 점은 기온이 급강하하는 시기보다는 급강하 후 회복하는 시기에 블랙아이스가 주로 발생함을 알 수 있었다. 이는 기온이 상승하는 시기에 상대 습도가 높아져 이슬점 온도와 기온의 차이가 작아지기 때문인 것으로 보인다.
블랙아이스 추정 모형은 복원 추출 시 이전 샘플링에서 오차를 보인 표본에 가중치를 두어 모형을 생성하는 부스팅 기법을 이용해 구축되었다. 전통적으로 분류 모형에 많이 사용된 AdaBoost, XGBoost, CatBoost 모형을 사용했다. 구축 모형 평가 결과, AdaBoost 모형을 제외하고 나머지 두 모형은 정확도(F1 점수) 90% 이상의 양호한 성능을 보였다. 입력 변수 기여도는 모형별로 다소 상이한 것으로 분석됐다. 본 연구 결과 적용 시 도로기상 관측망이 구축되지 않는 구간에서도 기상청에서 예보하는 기상 데이터를 이용해 신뢰성 있는 야간 블랙아이스 정보를 생성할 수 있다. 이는 운전자 정보 제공(VMS), 블랙아이스 발생 우려가 큰 구간에 대한 집중적인 예방적 도로관리(도로 순찰, 제설제 살포) 측면에서 효용성이 클 것으로 기대된다.
전술했듯이 본 연구에서 블랙아이스 발생 정보는 실측 정보가 아닌 노면 온도와 이슬점 온도를 이용해 계산된 정보이다. 또한 기상 데이터는 기상청에서 발표하는 동네예보(5km×5km) 데이터를 이용했기 때문에 동일 지역(5km×5km) 내 모든 도로 구간은 같은 블랙아이스 정보를 가질 수밖에 없다. 이는 교량, 터널, 교통량 등 도로나 교통 여건별로 다르게 나타날 수 있는 미세 구간(예. 표준링크)별 블랙아이스 정보 생성에 한계가 있음을 의미한다. 따라서 향후에는 블랙아이스 실측값, 표준링크별 기상 데이터를 이용해 좀 더 세밀한 분석이 필요할 것으로 판단된다. 아울러 정확한 노면 온도 수집 시각 정보가 없어, 시간 흐름에 따른 노면 온도 변화 및 그에 따른 블랙아이스 발생 매커니즘 분석에 한계가 있다. 향후 시계열적인 데이터 수집을 통한 추가적인 연구가 필요할 것으로 판단된다.