서론
관련문헌 고찰
1. 교통안전성 평가 연구
2. 주행궤적자료를 이용한 위치 예측 연구
3. 시사점
연구방법론
1. 연구 수행 과정
2. LSTM 기반 차량 위치 예측 모델
3. 위험상황 검지 지표
위험상황 검지 알고리즘 적용
1. 교차로 영상 검지기반 차량 궤적 데이터
2. 차량 위치 예측 결과
3. 위험상황 검지 결과
결론 및 향후연구과제
서론
도심도로 교차로 사각지대에 존재하는 차량에 대한 안전 서비스를 제공하고, 인접한 위험 요소를 인지하기 위한 V2X(vehicle-to-everything) 무선통신 기반의 BSM(basic safety message) 송수신 기술이 발달 되었다(SAE Standard J2735, 2016). BSM은 Radar, Lidar, camera 등 각종 첨단센서로부터 수집된 개별차량에 대한 속도, 가속도, 위치, 방향(heading) 등의 주행 정보를 포함한다. 주행의 편의와 운전자 및 보행자의 안전을 지원하기 위하여 주행 정보를 이용한 단기 미래의 이동체 위치 예측에 대한 연구가 활발히 수행되고 있다(Choi et al., 2018; Park et al., 2018; Schulz et al., 2018; Ma et al., 2019; Jeong et al., 2020). 특히 자율주행차량의 안전 및 수용성 측면에서 주변 객체에 대한 위치 예측 기술은 자율차의 주행에 영향을 미치는 객체인지 판단하는데 기여할 수 있다(Baek et al., 2020). 이에 따라, 도심도로 자율주행 환경에서 자율차의 차로변경 및 돌발상황 회피를 위해서는 단기적으로 위치를 예측함으로써 예측된 위치 정보를 기반으로 사전에 위험상황에 대한 경고정보를 제공할 필요가 있다.
도심도로와 같이 고층빌딩, 다양한 기하구조, 신호 운영 등의 복잡한 상황에서 효과적인 교통운영관리를 위해서는 안전한 도로주행이 가능하도록 개별차량 관점이 아닌 차량 간 상호작용 기반의 위험상황 판단이 요구된다. 개별차량의 미시적인 이동패턴을 나타내는 주행궤적자료는 실시간으로 사고개연성을 추정하고, 운전자에게 정보를 제공하는데 활용될 수 있으나(Bagdadi and Várhelyi, 2013; Wang et al., 2019; Xing et al., 2019), 데이터를 수집한 시점에서 이미 상충이 발생한 경우 운전자는 충돌을 회피할 시간이 부족하게 된다. 따라서 본 연구에서는 효과적인 정보제공을 위하여 선제적 교통안전 분석(proactive traffic safety analysis, PTSA) 기반의 개별차량 위치를 예측하고, 주행안전성 평가를 위한 위험상황 검지 방법론을 개발하고자 한다. 본 연구에서 PTSA는 교통사고 예방을 목적으로 사고발생 이전에 안전성 분석을 통해 능동적이고, 선제적인 대응책(countermeasure)을 도출하는 분석 기법으로 정의하였다. 차량의 위치를 예측하여 검지된 위험상황 정보는 I2V(infrastructure-to-vehicle) 무선통신의 지원을 받아 차량 내 경고알람이 표출될 수 있으며, 이는 자율차 및 운전자에게 사고 회피 행동을 보다 효과적으로 수행할 수 있는 기회를 제공할 수도 있다.
본 연구의 구성은 다음과 같다. 2장에서는 개별차량 위치 예측 기술 동향과 안전성 평가 관련 지표에 대한 문헌을 검토하였다. 3장에서는 차량 위치 예측 기반 위험상황 검지 방법론에 대해 서술하였다. 4장에서는 교차로 영상검지 기반 차량 주행궤적자료를 이용하여 제안된 알고리즘을 적용하였다. 마지막 장에서는 본 연구의 결론 및 향후 연구과제에 대해 서술하였다.
관련문헌 고찰
본 연구는 개별차량의 위치 예측을 기반으로 주행안전성을 평가하고 위험상황을 검지하는 기법을 개발하고자 한다. 이와 관련하여 위치 예측 기술 동향을 파악함으로써 본 연구의 방법론을 개발하는데 활용하였다. 또한, 예측된 위치에서 위험상황을 검지하는데 있어 교통안전 대체 평가지표(Surrogate safety measure, SSM)를 검토하고 기존 연구와의 차별성을 제시하였다.
1. 교통안전성 평가 연구
교차로에서 개별차량 관점이 아닌 차량 간 상호작용 분석을 통한 사고개연성 추정은 TTC(time-to-collision), PET(post encroachment time) 등 다양한 surrogate safety measure(SSM) 산출을 통해 개별차량 및 교통류의 위험정도를 정량적으로 판단하는데 활용되었다(Archer and Young, 2010; Pirdavani et al., 2010; Dijkstra, 2013; Sobhani et al., 2013). 도심도로 교차로에서의 상충 유형은 차량 간 상호작용에 대해 collision course, crossing course, non-crossing course로 구분할 수 있으며, 두 차량의 경로를 기반으로 충돌 지점을 판단하고 사고개연성을 추정할 수 있다(Laureshyn et al., 2010). 차량과 보행자 간의 상호작용을 고려하여 위험 이벤트(critical event)를 검지한 연구에서는 TTC, PET, GT(gap time)을 이용하여 충돌 위험성과 심각도를 평가한 것으로 보고되었다(Kathuria and Vedagiri, 2020). 또한, 차량과 보행자 간의 PET가 5초 이상일 경우 충돌은 1%로 매우 드물게 발생하지만, PET가 1초 이하일 경우는 위험상황이 약 85%로 빈번하게 발생한 것으로 나타났다(Yue et al., 2020). 사고 발생 이전에 두 이동체의 주행특성(속도, 가속도, yaw rate 등) 분석을 통해 상호작용 기반의 사고 개연성을 추정하는 것은 도로 이용자에게 위험상황 정보제공을 통한 사고예방에 기여할 수 있다고 보고되었다.
2. 주행궤적자료를 이용한 위치 예측 연구
교통안전 측면에서 도로 이용자에게 위험상황 경고 정보를 사전에 제공하기 위하여 위치 예측 기술이 접목될 경우 더욱 효과적인 사고예방을 기대할 수 있다. 차량 위치 예측을 통한 위험상황 검지는 능동적이고 선제적인 안전성 평가를 수행하는데 핵심 기술로 적용될 수 있다. 기존에 물리기반의 등속도(Constant Velocity, CV) 모델과 칼만필터(Kalman-filler) 모델을 이용하여 차량의 궤적을 예측하는 연구가 수행되었으나(Lin et al., 2000; Ammoun and Nashashibi, 2009; Barrios and Motai, 2011; Schulz et al., 2018), 큰 오차가 발생하는 문제점을 해결하기 위하여 딥러닝 모델이 적용되었다(Phillips et al., 2017; Park et al., 2018; Ma et al., 2019; Jeong et al., 2020). Recurrent neural network(RNN)와 long-short term memory(LSTM)은 주행궤적과 같이 시간에 대해 순차적으로 관측된 시계열 데이터의 패턴을 예측하는데 우수한 모델이며, LSTM은 gradient vanishing 및 gradient exploding 문제를 가지는 RNN의 한계를 극복하고자 개발된 모델이다(Kilian and Siegelmann, 1996; Hochreiter and Schmidhuber, 1997). 도시 교통 네트워크에서 이동하는 차량의 방대한 궤적을 분석하기 위하여 도심도로 네트워크를 일정 간격의 셀(cell) 또는 그리드(grid)로 구분하여 차량의 궤적을 예측한 연구가 보고되었다. Choi et al.(2018)은 RNN을 이용하여 셀의 시퀀스로 나타낸 차량의 궤적을 예측하였으며, Kim et al.(2017)은 주변차량이 점유할 확률이 높은 grid를 예측하기 위하여 LSTM을 적용하였다. Prediction term이 2초인 경우보다 0.5초인 경우의 x축 위치 오차는 약 4배, y축 위치 오차는 약 3배 낮은 것으로 분석되었다. 고속도로를 대상으로 구현한 Next Generation SIMulation(NGSIM)으로부터 수집된 개별차량 주행궤적 자료를 이용하여 종방향과 횡방향 위치를 예측한 연구 또한 prediction horizon이 짧을수록 예측 정확도가 높은 것으로 나타났다(Altché and de La Fortelle, 2017; Deo and Trivedi, 2018; Xin et al., 2018).
3. 시사점
기존 연구에서는 시뮬레이션 또는 실도로(교차로)에서 수집된 주행궤적자료를 이용하여 차량 간 상호작용 분석을 통한 위험상황을 검지하는 방법에 대한 연구를 주로 수행하였다. 기존의 위험상황 검지 기술에 위치 예측이 사전에 수행될 경우 보다 능동적이고 선제적인 분석 기술로 발전시킬 수 있을 것이다. 그러나 time scale parameter(TSP)와 딥러닝 알고리즘 학습에 필요한 하이퍼파라미터(hyperparameter)를 연계하여 최적화된 모델을 기반으로 선제적으로 위험상황을 검지하는 알고리즘의 개발을 위한 노력은 미흡하다. TSP는 시계열 기반의 교통자료를 이용하여 단기 예측 모델을 구축할 경우 예측 정확도에 영향을 미치는 파라미터로 rolling step, rolling horizon, prediction horizon으로 구분된다(Ishak and Al-Deek, 2002). 따라서 본 연구에서는 LSTM을 이용하여 차량 위치 예측 정확도가 우수한 최적화된 모델을 도출하고, 예측된 위치 정보를 기반으로 차량 간 상호작용 분석을 통해 교통사고 발생 개연성이 높은 위험상황 검지 알고리즘을 개발하고자 한다. 본 연구에서 제시한 방법론은 I2V 무선통신을 기반으로 위험상황 경고정보를 개별차량에게 제공함으로써 교차로 사고예방 및 안전성 증진을 위한 지원기술로 활용될 것으로 기대된다.
연구방법론
1. 연구 수행 과정
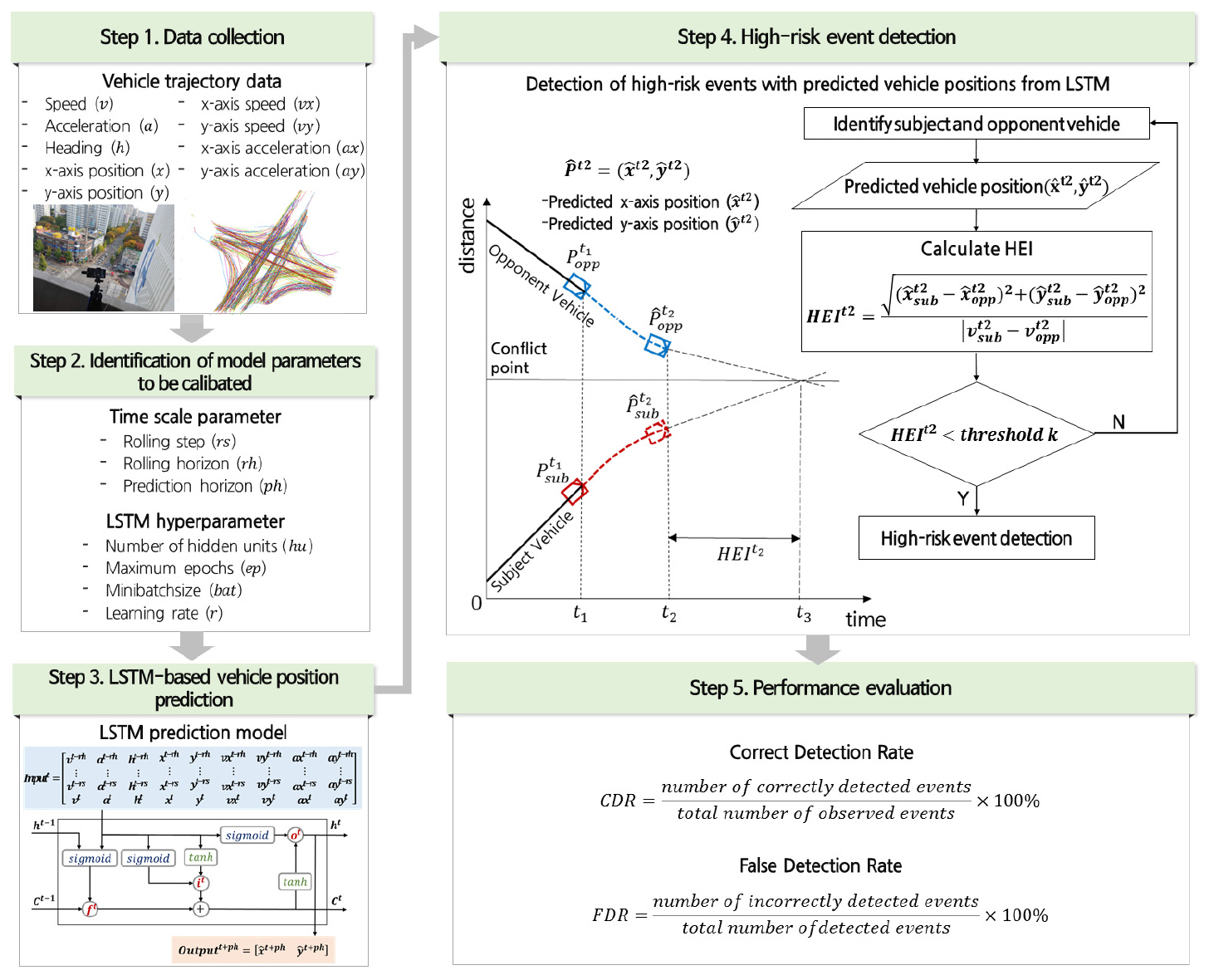
본 연구에서 선제적 교통안전 분석(proactive traffic safety analysis, PTSA)은 교통사고 예방을 목적으로 사고 발생 이전에 안전성 분석을 통해 능동적이고, 선제적인 대응책(countermeasure)을 도출하는 분석 기법으로 정의하였다. 본 연구에서 제안하고자 하는 차량 위치 예측 기반 위험상황 검지 방법론은 PSTA의 핵심 기술로 Figure 1에 제시하였다. 첫 번째 단계에서는 교차로를 대상으로 수집된 개별차량의 속도, 가속도, 방향, x축 위치, y축 위치, x축 속도 및 가속도, y축 속도 및 가속도를 포함하는 주행궤적자료를 수집한다. 두 번째 단계에서는 위치 예측 모델을 구축하기 위해 요구되는 파라미터를 설정한다. 시계열 기반의 교통자료를 이용하여 단기 예측 모델을 구축할 경우 예측 정확도에 영향을 미치는 TSP 중 rolling step, rolling horizon, prediction horizon을 고려하였다. 또한, LSTM 모델의 하이퍼파라미터는 모델의 학습 및 수렴에 영향을 미치며, 하이퍼파라미터 조정을 통해 예측 오차가 최소화되도록 최적화를 수행하여야 한다. 본 연구에서 고려한 LSTM 모델의 하이퍼파라미터는 은닉층의 노드 개수(number of hidden units), 최대 에포크(maximum epochs), 미니배치사이즈(minibatchsize), 학습률(learning rate)이다. 세 번째 단계에서는 2단계에서 설정된 TSP에 따라 input data를 생성하고, LSTM 하이퍼파라미터가 적용된 모델을 학습시킨다. 모델로부터 도출된 위치 예측 데이터 는 위험상황 검지에 활용된다. 네 번째 단계에서는 위험상황을 정량화하기 위한 지표로 High-risk event indicator(HEI)를 정의하고, 두 차량이 예측된 위치에서 산출된 HEI가 임계값 이하일 경우 위험상황으로 검지한다. 기존의 TTC 개념으로 접근한 HEI는 두 차량이 추종, 차로변경, 교차 시 현재 주행상태와 같은 방향 및 속도로 주행할 경우 충돌이 발생하기까지 남은 잔여 시간을 의미한다. 마지막 단계에서는 위험상황 검지 정확도를 도출하기 위한 성능척도로 correct detection rate(CDR)와 false detection rate(FDR)를 도출한다. CDR은 관측된 총 위험상황 발생 횟수 중 위험상황을 검지한 비율이고, FDR은 검지된 총 위험상황 건수 중 잘못 검지된 위험상황 건수의 비율로 정의된다. 두 성능척도는 0에서 100 사이로 산출되며, CDR은 높을수록 FDR은 낮을수록 위험상황 검지 정확도가 우수한 것을 의미한다.
2. LSTM 기반 차량 위치 예측 모델
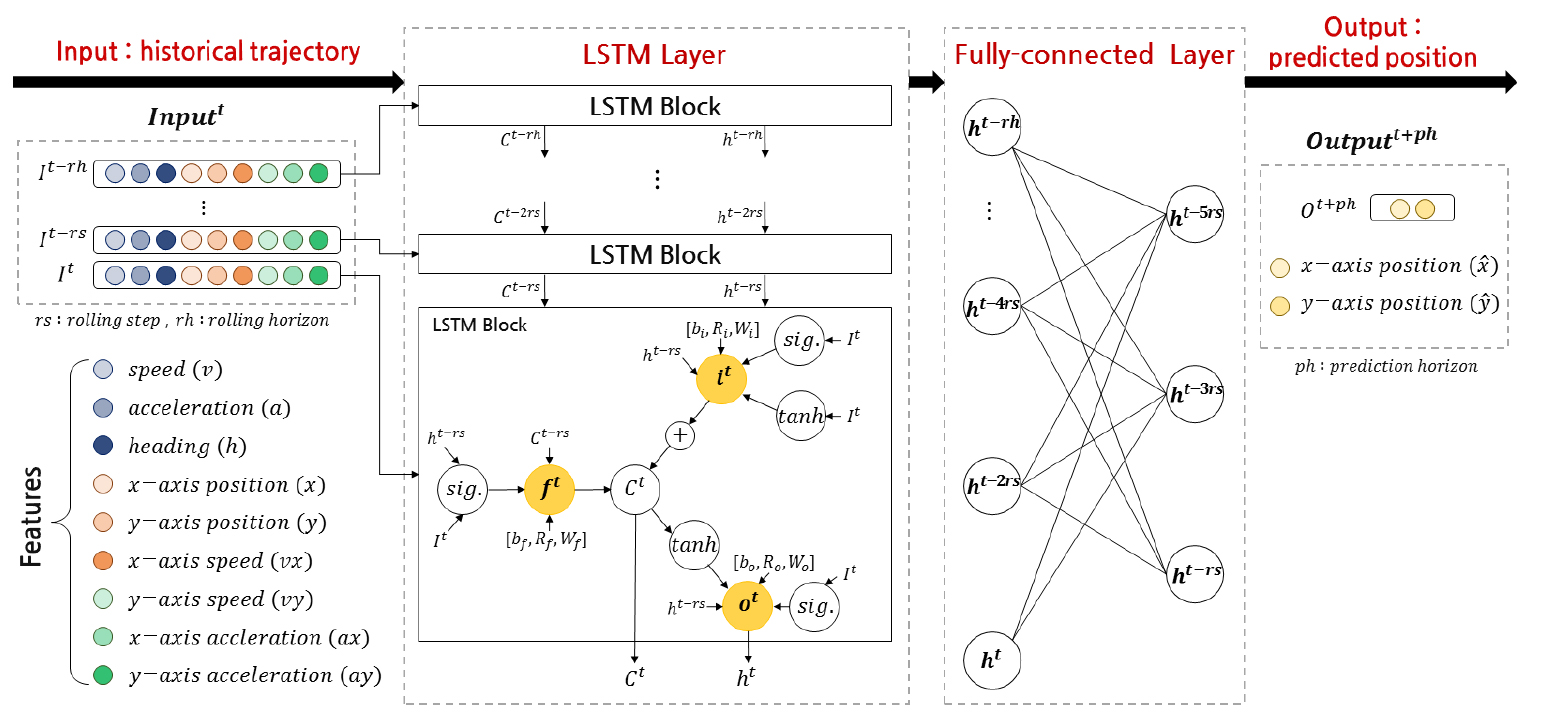
차량 위치 예측을 위한 LSTM 모델의 구조는 Figure 2에 제시하였다. 시계열 기반의 교통자료를 이용하여 예측 모델을 구축할 경우 rolling step(), rolling horizon(), prediction horizon()를 포함한 TSP 설정이 요구된다. 시점의 주행 궤적자료는 로 나타낼 수 있으며, 주행속도 , 가속도 , 방향각 , x축 위치 , y축 위치 , x축 속도 및 가속도 , 그리고 y축 속도 및 가속도 을 포함한다. 이때, input data()는 TSP 중 과거 이력자료에 대한 시간 간격을 의미하는 와 과거 이력자료에 대한 기간을 나타내는 을 고려하여 로 생성된다. LSTM layer 내에 LSTM block은 현재 셀의 입력값()과 과거 셀의 상태 값()을 사용해 현재 셀의 상태 값()을 계산하는 구조이다. 상태 값은 input weight , recurrent weight R, bias 의 조정을 통해 도출되며, , , 와 같이 행렬로 나타낼 수 있다. 여기서 는 입력 게이트(input gate), 는 손실 게이트(forget gate), 는 출력 게이트(output gate)이다. 손실 게이트는 현재의 입력값이 과거의 상태 값과 함께 시그모이드(sigmoid) 출력값을 도출하는 셀을 의미한다. 시그모이드는 0-1 사이의 값을 출력하고 과거의 메모리 셀()과 곱해져서 시그모이드 출력값이 1인 경우 기억을 그대로 유지한다. 예를 들어, 시그모이드 출력값이 0.8일 경우 80%의 과거 기억만을 저장하고, 20%의 기억은 소멸된다. 또한, 현재의 입력값과 과거의 상태 값을 계산하여 저장할 새로운 정보의 양을 결정하는 셀을 입력 게이트라고 하며, 출력값을 내보내기 전 메모리 셀과 상태 값을 계산하는 셀을 출력 게이트라고 한다. 각 게이트의 계산식은 Equation 1에 제시하였다. Fully-connected layer는 LSTM layer로부터 출력된 모든 상태 값을 연결시켜 1차원 배열의 형태로 통합하고, 평활화한다. 최종적으로 output layer에서는 fully-connected layer로부터 뉴런을 전달받아 미래에 대한 예측 기간인 에 해당하는 위치 데이터 을 출력한다.
여기서, : time step t에서 입력 게이트
: time step t에서 손실 게이트
: time step t에서 출력 게이트
: input weight
: recurrent weight
: bias
: time step t에서 입력 값
: time step t-1에서 상태 값
딥러닝 모델의 하이퍼파라미터는 모델의 학습 및 수렴속도에 영향을 미치며, 하이퍼파라미터 조정을 통해 예측 오차가 최소화되도록 최적화를 수행하여야 한다. 본 연구에서는 다양한 하이퍼파라미터 값 설정을 통해 파라미터 시나리오를 설계하고, 예측 오차가 가장 작은 모델에 대해 최적 파라미터 셋을 도출하고자 한다. LSTM 모델의 하이퍼파라미터 중 은닉층의 노드 개수(number of hidden nodes), 에포크(epoch), 배치사이즈(batch size), 학습률(learning rate)에 대한 값을 조절하였다. LSTM의 은닉층은 노드(node)에서 활성화 함수를 통해 결과 값을 출력하며, 일반적으로 신경망의 성능을 높이기 위하여 은닉층의 노드 개수를 늘려 계층 구조를 깊게 구축한다. 하지만, 노드의 개수가 매우 많을 경우에는 연결 가중치도 많아져 복잡한 모델이 되기 때문에 과대적합(over-fitting) 문제가 발생할 수 있고, 계산량이 급증하여 학습시간이 오래 소요되기 때문에 적정 값 설정이 요구된다. 또한, 에포크는 훈련데이터의 학습 횟수를 결정하는 파라미터로, 에포크 값이 매우 작을 경우 과소적합(under-fitting) 문제가 발생하고, 에포크 값이 매우 클 경우 과대적합 문제가 발생할 수 있다. 배치사이즈는 하나의 배치에 포함되는 샘플의 수를 의미하며, 여기서 배치는 훈련 데이터의 샘플을 여러 개로 묶어 학습에 이용되는 그룹을 의미한다. 하나의 배치에 포함된 모든 샘플을 이용하여 가중치와 편향을 수정하기 때문에 배치 사이즈는 가중치와 편향을 수정하는 간격으로 표현한다. 마지막으로, 학습률은 학습의 속도를 결정하는 상수로, 값이 작을수록 학습시간이 오랜 시간 소요되며 국소 최적해(local minimum) 문제가 발생할 수 있다. 반면에 학습률이 너무 커져도 오차가 작은 지점으로 수렴되기 어려운 문제(overshooting)가 발생한다. 따라서 하이퍼파라미터 설정값에 따라 알고리즘이 달라지기 때문에 우수한 성능을 도출하기 위하여 다양한 파라미터 값에 대한 고려가 필요하다. MathWorks에서 제공하는 공학용 소프트웨어인 MATLAB에서 제시한 LSTM 모델의 하이퍼파라미터에 대한 설명은 Mathworks-trainingoptions를 참고하여 Table 1에 제시하였다.
Table 1.
Hyperparamter for LSTM (Mathworks-trainingoptions)
3. 위험상황 검지 지표
본 연구에서는 예측된 위치 데이터를 이용하여 차량 간 상호작용 기반의 위험상황을 검지하고자 한다. 개별차량의 최근접 차량을 상호작용 차량으로 정의하였으며, 상호작용 차량은 주체가 되는 차량의 움직임 변화로 인하여 속도와 위치가 변할 것이다. 본 연구에서는 위험상황을 정량화하기 위한 지표로 기존의 TTC 개념과 유사한 High-risk event indicator(HEI)를 정의하였으며, HEI는 두 차량이 추종, 차로변경, 교차 시 현재 주행상태와 같은 방향 및 속도로 주행할 경우 충돌이 발생하기까지 남은 잔여 시간을 의미한다. TTC 임계값을 설정한 기존 연구를 참고하여(El-Basyouny and Sayed, 2013; Sacchi et al., 2013; Sacchi and Sayed, 2016), HEI가 1.5초, 2초, 2.5초, 3초 이하인 경우에 대한 다양한 위험상황을 정의하였다. 향후 제안된 기술의 실도로 적용 시 교통운영자가 정의한 위험상황에 따라 교차로 모니터링이 가능할 것으로 기대된다. HEI는 LSTM으로부터 예측된 시점의 x축 위치 와 y축 위치 , 그리고 속도 자료를 이용하여 Equation 2와 같이 산출된다.
여기서, : 시점에서 예측된 주체 차량의 x축 위치(m)
: 시점에서 예측된 상호작용 차량의 x축 위치(m)
: 시점에서 예측된 주체 차량의 y축 위치(m)
: 시점에서 예측된 상호작용 차량의 y축 위치(m)
: 시점에서 주체 차량의 속도(m/s)
: 시점에서 상호작용 차량의 속도(m/s)
: 미래에 대한 예측 기간 prediction horizon(s)
위험상황 검지 알고리즘 적용
1. 교차로 영상 검지기반 차량 궤적 데이터
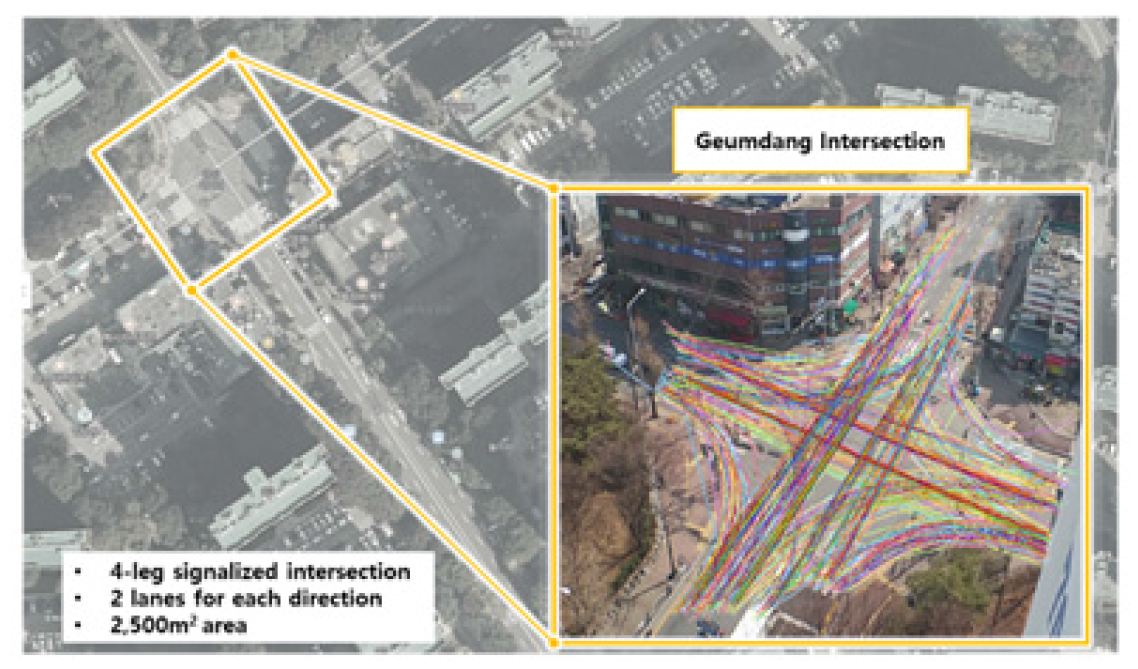
교차로 영상검지 기반의 차량 주행궤적자료는 Kim(2019) 연구에서 수집되었으며, 해당 데이터는 본 연구에서 제안된 방법론에 적용되었다. Figure 3에 제시된 분석대상 구간은 경기도 광명시에 위치한 금당사거리로 가로수, 높은 건물 등으로 인해 차량이나 배경이 가리지 않는 양방향 4차로 4지 신호교차로이다. 사진이나 영상은 3차원의 물체를 2차원으로 표현한 것으로 물리적인 원근 특성이 발생할 수 있기 때문에 왜곡에 대한 영향을 최소화하기 위하여 분석대상 구간의 약 30m 높이의 장소에서 촬영되었다(Kim, 2019). 영상 추적 범위는 가로, 세로 각각 약 50m이며, 2,500m2에 해당하는 면적이다. 자료 수집 범위는 2018년도 9월 19일, 오전 10시에서 오후 5시 사이의 총 7시간이다. 분석 범위 내에 총 11,649대의 차량에 대해 391,326개의 데이터 샘플이 수집되었다. 수집된 데이터 중 HEI 임계값 1.5초, 2초, 2.5초, 3초를 기준으로 위험상황은 각각 123건, 233건, 384건, 575건이 발생하였다. 개별차량의 주행궤적 자료는 0.1초 단위로 수집된 주행속도(m/s), 가속도(m/s2), 방향각(degree), x축 위치(pixel, m), y축 위치(pixel, m), x축 속도(m/s) 및 가속도(m/s2), y축 속도(m/s) 및 가속도(m/s2)를 포함한다. 차량의 중심부에 대한 x축 및 y축 위치는 영상 검지 범위의 좌측 하단을 원점으로 하는 픽셀 위치이며, 10pixel은 1m를 의미한다.
1) 모델 변수 설정
수집된 개별차량의 주행궤적자료는 input data와 output data로 구분되며, Equation 3과 같이 TSP를 고려하여 연속된 시계열 형태의 데이터로 생성된다. TSP는 시계열 기반의 교통자료를 이용하여 단기 예측 모델을 구축할 경우 예측 정확도에 영향을 미치는 파라미터로 rolling step(), rolling horizon(), prediction horizon()을 포함한다(Ishak and Al-Deek, 2002). 개별차량 에 대해 시점의 주행 궤적자료는 로 나타낼 수 있다. 이때 input data는 와 를 고려한 9개의 feature vector로 설정된다. 또한 output data는 를 고려하여 예측하고자 x축과 y축의 위치로 설정하였다.
여기서, : 차량 , 시점 에 대한 state-space를 나타내는 input data
: 차량 , 시점 에 대한 state-space를 나타내는 output data
: 차량 의 주행궤적자료
: 주행속도(m/s)
: 가속도(m/s2)
: 방향각(degree)
: x축 위치(m)
: y축 위치(m)
: x축 속도(m/s)
: y축 속도(m/s)
: x축 가속도(m/s2)
: y축 가속도(m/s2)
: rolling step(s)
: rolling horizon(s)
: prediction horizon(s)
2) 파라미터 시나리오
본 연구에서는 TSP와 딥러닝 하이퍼파라미터를 연계하여 차량 위치 예측 모델의 최적화를 수행하였다. TSP는 수집된 데이터의 특성에 따라 결정될 수 있다. Rolling step은 데이터 수집 간격에 따라 결정되며, 주행궤적자료가 0.1초 단위로 수집될 경우 rolling step은 0.1초 이상으로 설정한다. 또한, rolling horizon은 prediction horizon보다 큰 값으로 설정되며, 개별차량에 대한 데이터 수집 건수에 따라 결정된다. 본 연구에서 수집된 85percentile에 해당하는 개별차량의 데이터 수집 건수는 약 60건으로 6초에 해당하는 주행궤적자료이다. 이에 따라, Table 2와 같이 prediction horizon은 1초, 2초로 설정하였으며, rolling horizon은 2초, 3초, 4초, 5초로 설정하였다. 예를 들어, prediction horizon 1초, rolling horizon 5초에 대한 파라미터 시나리오의 경우 6초 이상을 주행한 궤적자료를 LSTM 모델에 적용하였다. 향후 더 넓은 영상 추적 범위에서 더 많은 주행궤적자료가 수집될 경우 보다 먼 미래의 위치를 예측할 수 있을 것이다. 설정된 TSP에 따라 생성된 데이터는 training set(70%)과 test set(30%)으로 구분하였으며, 이때 training set은 LSTM 모델을 구축하는데 활용되고 구축된 모델을 검증하기 위하여 test set을 적용한다.
Table 2.
The number of data by time scale parameters
본 연구에서 설정한 LSTM 하이퍼파라미터 시나리오는 기존 문헌에서 고려된 범위를 기반으로 정의된 MATLAB 기본값(default)을 참고하여(Bishop, 2006; Murphy, 2012; Pascanu et al., 2013) Table 3과 같이 설정하였다. LSTM 모델은 Adam(ADAptive Moment estimation) optimizer를 사용하여 학습한다(Kingma and Ba, 2014). MaxEpochs의 경우는 기본값인 30보다 매우 클수록 과대적합 문제가 발생할 수 있으며, InitialLearnRate가 증가할수록 오차가 작은 지점으로 수렴되지 않는 문제가 발생하여 예측 정확도가 떨어질 수 있다. 또한, MiniBatchSize는 기본값인 128보다 매우 작을수록 학습에 이용되는 훈련데이터의 그룹 수가 증가하기 때문에 모델의 가중치 및 편향의 계산량이 급증하는 문제가 발생할 수 있다. 본 연구에서는 기존 연구에서 고려된 하이퍼파라미터의 범위를 시나리오에 반영하였다(Altché and de La Fortelle, 2017; Kim et al., 2017; Deo and Trivedi, 2018; Xin et al., 2018). 따라서 본 연구에서 적용한 파라미터 시나리오는 TSP 6개와 하이퍼파라미터 81개의 조합을 통해 총 486개로 설정하였다. 이때, 개발된 486개의 위치 예측 모델 중 TSP를 기준으로 예측 정확도가 가장 우수한 하이퍼파라미터를 도출함으로써 모델 최적화를 수행하였다.
Table 3.
Details of hyperparameters for LSTM
| Hyperparameters | Details | Number of cases |
| numHiddenUnits | 50, 100, 150 | 3 cases |
| MaxEpochs | 30, 50, 100 | 3 cases |
| MiniBatchSize | 32, 64, 128 | 3 cases |
| InitialLearnRate | 0.001, 0.005, 0.01 | 3 cases |
2. 차량 위치 예측 결과
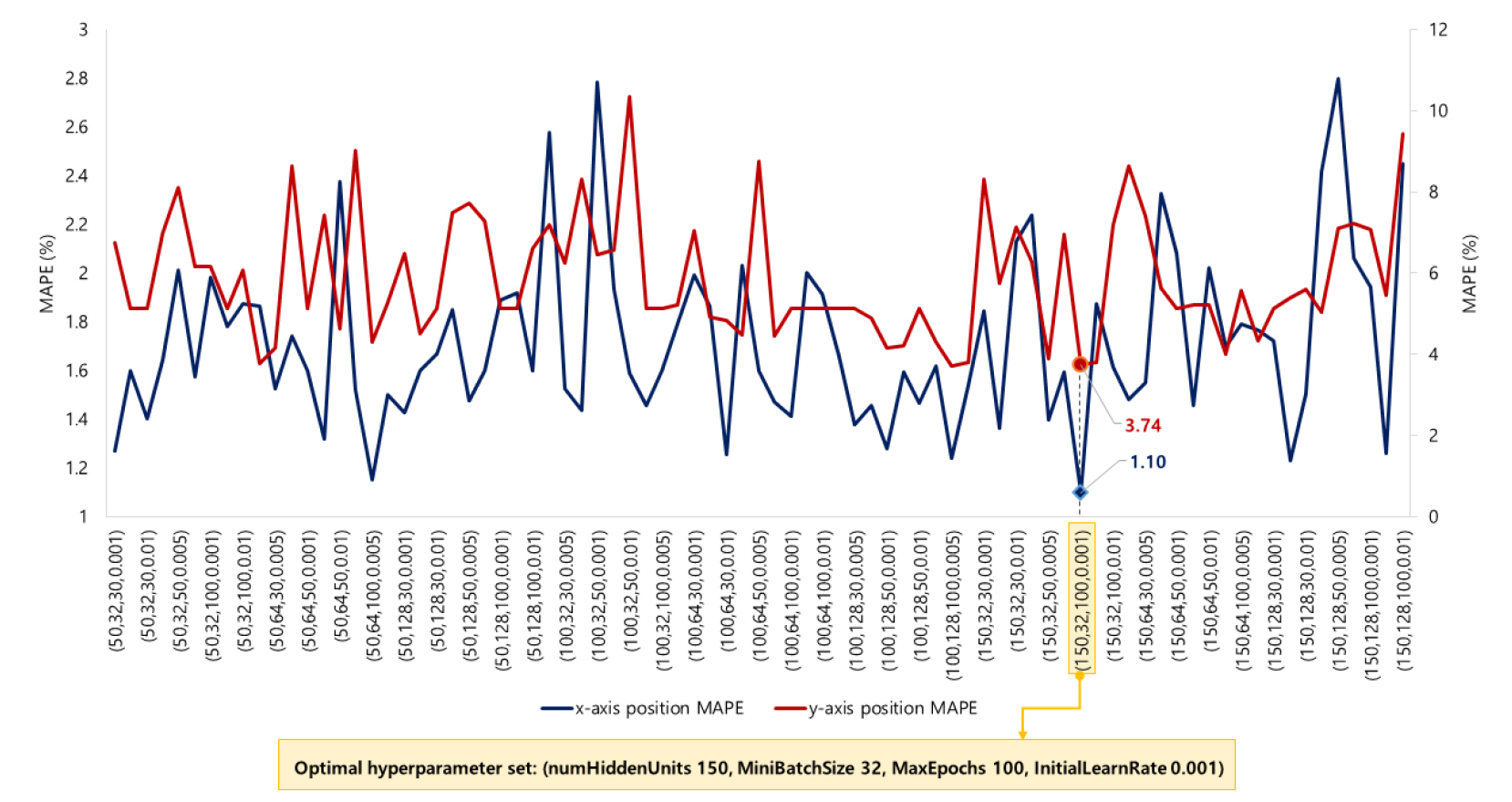
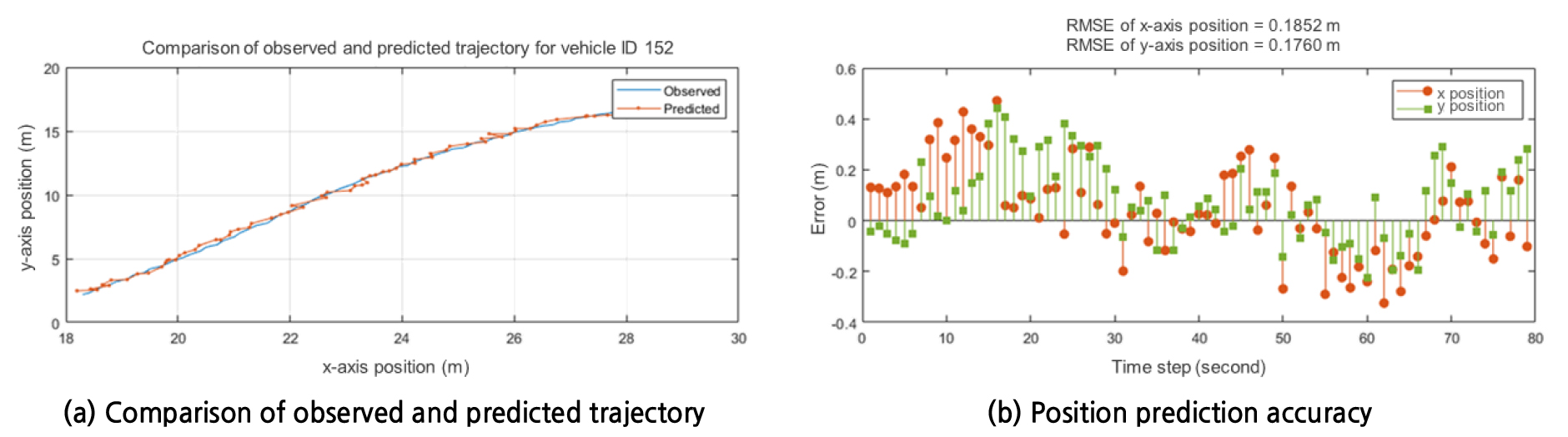
LSTM을 기반으로 예측된 위치의 오차는 mean absolute percentage error(MAPE)와 root mean square error(RMSE)를 이용하여 도출되었으며 각각 Equation 4, Equation 5와 같이 산출된다. Rolling horizon 및 prediction horizon에 따라 도출된 각 81개의 LSTM 모델 중 x축과 y축 위치에 대해 최소 RMSE 및 MAPE를 가지는 하이퍼파라미터는 Table 4와 같다. RMSE를 기준으로 위치 예측 정확도가 가장 우수한 최적 파라미터 셋은 rolling horizon 5초일 경우, 은닉층의 노드 개수 150, 최대 에포크 32, 미니배치사이즈 100, 초기학습률 0.001로 도출되었다. 이에 해당하는 RMSE는 x축 0.61m, y축 0.57m이며, MAPE는 x축 1.10%, y축 3.74%로 분석되었다. LSTM 하이퍼파라미터 셋 변화에 따른 x축 및 y축 위치 오차에 대한 예시를 Figure 4에 제시하였다. 또한, 임의의 차량에 대해 관측 및 예측된 주행궤적의 예시는 Figure 5(a)에 제시하였으며, x축과 y축 위치의 RMSE에 대한 예시는 Figure 5(b)와 같다.
여기서, : 실제 위치()
: 예측된 위치()
: 데이터 샘플 수
여기서, : 실제 위치()
: 예측된 위치()
: 데이터 샘플 수
Table 4.
Result of optimal hyperparameters by rolling horizon and prediction horizon
3. 위험상황 검지 결과
과거 5초의 주행궤적 자료를 이용하여 1초 뒤 위치가 예측된 차량은 1,491대이다. 개별차량에 대해 최근접 차량을 추출하고, 두 차량의 상호작용 분석을 통해 위험상황을 검지하였으며, 이에 적용된 데이터 샘플 수는 13,067개이다. 신호교차로에서 신호위반을 하지 않는다는 가정에 따라 최근접 차량은 동일 방향을 주행하는 선 ‧ 후행 차량, 서로 다른 방향을 주행하는 좌회전-우회전 차량, 직진-우회전 차량이 될 수 있다. 위험상황은 두 차량의 속도와 예측된 위치를 이용하여 HEI 산출을 통해 정량화된다. HEI의 임계값은 1.5초, 2초, 2.5초, 3초로 설정하였으며, 임계값 이하일 경우는 위험상황으로 검지하였다. 예측된 위치 데이터를 이용하여 위험상황 검지에 대한 성능척도로 correct detection rate(CDR)와 false detection rate(FDR)를 각각 Equation 6과 Equation 7로 정의하였다. CDR은 관측된 위험상황을 위험하다고 검지한 비율이며, FDR은 검지된 총 위험상황 건수 중 잘못 검지된 위험상황 건수의 비율이다. CDR과 FDR은 0-100 사이로 산출되며, CDR은 높을수록 FDR은 낮을수록 위험상황 검지 정확도가 우수한 것을 의미한다. HEI 임계값을 기준으로 도출된 성능척도의 값은 Table 5에 제시하였다. 임계값 3초를 기준으로 관측된 총 위험상황 건수 574건 중 위험하다고 검지한 건수가 560건으로 CDR은 97.56%로 산출되었다. 반면 임계값 2초를 기준으로 검지된 총 위험상황 건수 233건 중 잘못 검지된 위험상황이 4건으로 FDR은 1.72%로 도출되었다. 전반적으로 HEI 임계값별 CDR은 94.31-97.56%, FDR은 1.72-5.69%로 본 연구에서 제안된 알고리즘의 적용성을 확인하였다.
여기서, : 실제 위험상황을 위험하다고 검지한 건수
: 관측된 총 위험상황 발생 건수
여기서, : 잘못 검지된 위험상황 발생 건수
: 검지된 총 위험상황 발생 건수
결론 및 향후연구과제
개별차량의 주행궤적 자료를 이용하여 위치 예측 기반의 차량 간 상호작용 분석을 통해 교통사고 발생 개연성이 높은 위험상황을 검지하는 것은 선제적 교통안전성 분석의 핵심 기술이라 할 수 있다. 본 연구에서는 교차로에서 수집된 총 391,326개의 주행궤적 데이터 샘플을 이용하여 LSTM을 기반으로 위치를 예측하였다. 위치 예측 정확도가 가장 우수한 모델의 RMSE는 x축 위치 0.61m, y축 위치 0.57m로 분석되었다. 추가적으로 예측된 위치 데이터를 이용하여 위험상황을 검지한 결과, HEI 3초를 기준으로 약 98%의 정확도로 도출되어 제안된 방법론의 적용성을 확인하였다.
본 연구에서 제안된 기술은 교통운영과 자율차 제어 두 가지 관점에서 활용될 수 있을 것으로 기대된다. 특히, 비신호교차로의 경우 자율차의 자체 센서 기능만으로 온전히 주변 상황을 인지하고 돌발상황에 대처하며 주행하기에 한계가 있다. 이에 따라, 교통운영 측면에서는 자율차가 비신호교차로에서 좌회전을 하려는 경우 자율차의 안전성이 확보된 시점에서 좌회전 신호를 부여(left signal warrant)하는 것이 가능할 것이다. 또한 자율차 제어 측면에서는 비보호 좌회전 시 진행방향이 다른 직진, 우회전, 좌회전 차량과의 위험상황 정보를 I2V 무선통신을 통해 자율차에게 제공하여 교차로를 안전하게 통과하는데 거동을 결정할 수 있는 선제적 교통안전 정보로 활용 가능하다. 본 연구에서 제안된 방법론을 실질적으로 적용하기 위해서는 더욱 긴 주행궤적을 수집할 수 있는 넓은 영상 추적 범위가 요구된다. 향후 연속된 교차로를 대상으로 추적된 주행궤적자료 수집을 통해 자율차 거동 결정 또는 일반차량 운전자의 충돌회피를 위한 충분한 시간을 제공하기 위하여 실질적으로 적용 가능한 모델 개선 및 결과 도출이 필요할 것이다. 추가적으로 본 연구에서 제시한 방법론은 교차로뿐만 아니라 고속도로의 평면선형, 종단선형, 복합선형 구간과 터널, 교량 등 시설이 포함된 구간 등 다양한 분석범위에 적용될 수 있다. 예를 들어, 국내 C-ITS 시범사업구간을 주행하는 C-ITS 단말기 장착 차량에 대해 주행정보 수집, 선행차량 위치 예측, 주행안전성 평가를 통한 V2X 기반 선제적 교통안전정보를 제공함으로써 안전성 증진에 기여할 것으로 판단된다.
본 연구에서 제시한 차량 위치 예측기반 주행안전성 평가를 위한 위험상황 검지 기술에 대한 신뢰도를 높이기 위해서는 다음과 같은 추가적인 연구가 필요하다. 첫째, 본 연구에서는 일부 샘플 데이터를 활용하여 분석하였으나, 센서 기반 DB를 구축하여 보다 다양한 이동체 궤적 예측이 가능하도록 하는 것이다. 이동체 궤적 자료를 무한히 수집하여 빅데이터 분석을 위한 데이터 셋이 구축될 경우, 신호기 고장, 보행자 무단횡단과 같은 돌발 상황에 대한 in-regular trajectory에 대해서도 위치를 예측할 수 있다. 또한, 수집된 영상 데이터의 원근 특성 상 거리 계산에 있어 왜곡이 발생할 수 있기 때문에 왜곡 보정을 통한 신뢰도 높은 결과를 제시할 것이다. 둘째, 이동체 위치 예측 오차를 반영한 위험상황 검지가 수행되어야 한다. 두 상호작용 이동체가 실제 위험상황임에도 불구하고 위치 오차로 인해 안전한 상황으로 예측하는 문제가 발생할 수 있다. 따라서 위험상황을 검지하는데 있어서 수용할 수 있는 오차범위 설정이 요구된다. 설정된 오차범위는 위험상황 검지의 신뢰성과 직결되는 문제이다. 셋째, RNN, deep neural network(DNN), convolutional neural network(CNN)와 같은 다양한 방법론을 고려한 연구가 수행되어야 한다. 여러 모델의 하이퍼파라미터 조정을 통한 위치 예측 정확도를 비교하여 오차를 최소화하기 위한 모델 개선이 필요하다. 딥러닝 모델을 기반으로 예측된 위치와 실제 위치 간의 차이를 나타내는 오차의 평균 비교를 통해 통계적 검증을 수행함으로써 분석 결과의 유의성을 판단할 수 있다. 이를 통해 본 연구에서 예측된 위치 기반의 위험상황 검지 결과와 여러 모델 간의 비교 및 평가가 가능할 것으로 기대된다. 교차로의 선제적 교통안전 분석을 위하여 향후 보행자, 이륜차 등 다양한 이동체의 궤적 자료를 이용할 경우 교통류 전반의 안전성 평가 및 모니터링이 가능할 것이다.