Real-time On-demand Service for Dynamic Route Generation Considering User Utility: A Case Study of Namyang New Town,  Hwaseong,  Gyeonggi-do

Juhyoun Youm; Jinhee Kim

doi:10.7470/jkst.2024.42.6.706

Preview

Article

Journal of Korean Society of Transportation. 31 December 2024. 706-723
https://doi.org/10.7470/jkst.2024.42.6.706

Real-time On-demand Service for Dynamic Route Generation Considering User Utility: A Case Study of Namyang New Town, Hwaseong, Gyeonggi-do

이용자 효용을 반영한 실시간 수요대응형 서비스 동적 경로 생성: 경기도 화성시 남양뉴타운을 중심으로

Juhyoun YOUM¹

Jinhee KIM²^*

염 주현¹

김 진희²^*

¹Combined Masters & PhD Course, Department of Urban Planning and Engineering, Yonsei University, Seoul 03722, Korea

²Associate Professor, Department of Urban Planning and Engineering, Yonsei University, Seoul 03722, Korea

¹연세대학교 도시공학과 석박사통합과정

²연세대학교 도시공학과 부교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/4.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/4.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

With advancements in big data and technology, on-demand public transportation services that process real-time reservations based on user requests and acceptance are gaining attention. Unlike fixed-route public transport, on-demand services dynamically generate routes according to demand, which may alter travel times as other users join. However, these variations can reduce user satisfaction and increase ride cancellations. This study proposes a framework incorporating a utility function, commonly used in service acceptance decision estimation, into the route-matching cost function of on-demand public transport. The dynamic route generation algorithm is based on an Insertion Heuristic with constraints such as maximum waiting time, additional in-vehicle travel time, and vehicle capacity. A simulation was conducted in Namyang New Town, Hwaseong, Gyeonggi-do, comparing vehicle travel time-based and user utility-based cost functions. Results demonstrated that integrating user utility into the dispatch algorithm improved performance, including travel delay ratio and service acceptance rates, thus enhancing user service efficiency. This suggests that applying user utility to dispatch algorithms can improve real demand capture and foster a flexible, user-centric service.

Keywords

acceptance rate

dynamic route generation

on-demand

stated preference

user utility

최근 빅데이터 수집 및 기술의 발전으로 실시간으로 사용자의 요청과 수락에 기반하여 예약이 확정되는 수요대응 대중교통 서비스가 주목받고 있다. 한편, 수요대응 대중교통은 수요에 기반하여 경로가 생성됨에 따라 전통적인 대중교통 서비스와 달리 타인의 서비스 호출로 인하여 승객의 통행시간의 변화가 발생한다. 그러나 통행시간의 변화는 이용자 관점에서 비효용을 야기한다는 점에서 실제 서비스 환경에서 이용자의 호출 취소가 발생할 수 있다. 이에 본 연구는 실시간 수요대응형 대중교통의 경로 생성 과정에 서비스 수락 의사결정 추정 연구에서 활용되고 있는 효용함수를 경로 매칭 비용함수에 접목시키는 프레임워크를 제시하였다. 동적 경로 생성은 삽입 휴리스틱 알고리즘을 기반으로 하되 최대 대기시간과 최대 추가 차내 통행시간, 차량 용량에 대한 제약조건을 추가하여 경로 탐색을 수행하였다. 또한, 제시한 프레임워크의 효과를 검증하기 위하여 시뮬레이션 실험을 수행하고 선행연구에서 제시한 차량 총 통행시간 기반의 경로 매칭 비용함수와 이용자 효용기반 비용함수 배차 결과를 운영자와 이용자 관점에서 비교하였다. 시뮬레이션은 실시간 수요대응 자율주행 대중교통 모빌리티 서비스 기술 개발 연구가 수행중인 경기도 화성시 남양읍 남양뉴타운을 중심으로 수행되었다. 시뮬레이션 실험 시 비용함수에 따른 경로 생성 결과물이 이용자의 서비스 수락에 미치는 영향을 판별하기 위하여 잠재선호 실험 기반의 수락률 모형을 적용하여 배차 정보에 따른 실 수락 여부를 판별하였다. 그 결과 이용자 효용을 배차 알고리즘의 비용함수에 적용하는 것이 이용자 서비스 효율을 나타내는 통행지연 비중과 서비스 수락 관점에서 더 우수한 결과를 보였으며, 총 차량 통행거리 대비 서비스 인원에 대한 운영자 관점 지표에 대하여 더 높은 수치를 보였다. 이를 통하여 향후 남양뉴타운과 같이 소도시 지역을 중심으로 수요대응형 대중교통 서비스를 운영함에 있어 이용자 효용을 배차 알고리즘에 적용하는 것이 실 수요를 확보하고 유동적이고 이용자 친화적인 서비스를 제공하는데 기여할 수 있음을 확인하였다.

키워드

수락률

동적 경로 생성

수요대응형

잠재선호

이용자 효용

MAIN

서론
선행연구
동적 경로 생성 알고리즘 구성 및 이용자 효용 적용 방법
1. 동적 경로 생성 알고리즘
2. 이용자 효용을 반영한 동적 배차 비용함수
3. 이용자 잠재선호 설문조사 및 서비스 수락률 모형 구성
시뮬레이션 실험
1. 시뮬레이션 실험 설계
2. 이용자 효용함수 추정 및 시뮬레이션 반영
실험 결과
1. 최대 대기시간 변수 실험 결과
2. 최대 추가 차내 시간 변수 실험 결과
3. 이용자 효용 가중치에 따른 실험 결과
결론

서론

수요대응형 대중교통 서비스는 이용자의 수요에 맞추어 유연하게 운행되는 교통 서비스로, 최근 빅데이터 수집 및 처리 기술의 발전으로 실시간 호출과 수락에 기반해 경로를 생성하는 다이나믹형 서비스 유형이 증가하고 있다. 다이나믹형 수요대응형 서비스는 고정된 운행시간표가 없으며, 수요에 따라 탄력적으로 승하차 위치와 경로가 결정되는 여객 운송사업으로, 현재 국내에서는 서울 은평구의 현대자동차 셔클, 인천 영종도의 I-MOD, 경기도 화성 동탄신도시의 똑버스 등 수도권 소도시 지역을 중심으로 운영 중이다.

다이나믹형 수요대응형 대중교통 서비스의 경로 알고리즘은 차량에 탑승 중인 승객들의 수요를 고려하면서, 실시간으로 호출된 수요를 탐색 시점의 차량 경로에 효율적으로 배정해야한다. 이 과정에서 탐색 시점 이전에 차량에 매칭된 승객 통행시간이 변화할 수 있다는 불확실성이 존재한다. 이러한 이유로 일부 연구에서는 통행시간 변화가 이용자에게 비효용을 야기할 수 있으므, 경로 매칭 시 이용자의 통행시간변화를 고려해야한다고 주장한다. 예를 들어, Nasri et al.(2021)는 고객 지향적 다이얼-어-라이드 문제(Customer-Oriented Dial-A-Ride Problem; CO-DARP) 개념을 통해 차량 통행시간 비용함수 기반 최적화 알고리즘에 탑승자별 최대 우회시간을 제약조건으로 설정하는 프레임워크를 제안했다.

한편, 수단 선택 또는 서비스 수락 연구에 따르면 접근시간, 대기시간, 차내 시간 등 통행을 구성하는 각 요소가 이용자의 효용에 미치는 영향이 다르다. 선행 연구에서는 차량의 통행시간과 대기시간의 스케일을 맞추기 위하여 임의의 가중치를 적용하고 있는 것으로 나타났으나, 통행시간 유형에 따라 이용자에게 미치는 효용이 다르다는 점을 간과하고 있다. 이에 본 연구는 실시간 호출에 따라 경로를 생성하는 서비스의 동적 경로 생성 알고리즘에 승객의 효용 함수를 적용하여, 이용자 관점에서의 서비스 효용을 차량 배차에 반영하고자 하였다또한, 제안된 배차 전략의 효과를 평가하기 위해 운영자와 이용자 관점에서 효과 지표를 구성하고, 이를 기반으로 차량 기반 배차 전략과 효용 기반 전략의 시뮬레이션 결과를 비교하였다.

다음 장에서는 수요대응형 대중교통 서비스 경로 생성 알고리즘과 밀접한 관련이 있는 다이얼-어-라이드 문제(Dial-A-Ride Problem; DARP)에 대한 선행 연구를 검토한다. 이어 3장에서는 본 연구에서 활용한 규칙 기반 동적 경로 생성 방법론을 비롯해 제안하는 차량 매칭 비용함수와 선행 연구에서 사용된 차량 총 통행시간 기반 비용함수를 설명한다. 4장에서는 차량 운행 가능 경로 및 시뮬레이션 비교 실험을 위한 제약 조건을 서술하고, 5장에서는 시뮬레이션 비교 실험 결과를 통해 비용함수별 효과 지표(수락 응답 수, 평균 수락률)를 제시한다. 마지막으로 본 연구의 의의 및 한계, 그리고 향후 연구 방향을 정리한다.

선행연구

수요대응형 대중교통 서비스 경로 생성 문제는 출발지와 목적지 간 승차 및 이동 요청을 처리하는 다수의 이용자를 위한 차량 경로와 일정을 설계하는 DARP로 정의할 수 있다. DARP는 Vehicle Routing Problem(VRP)를 일반화한 것으로, 일련의 제약 조건 아래 가능한 많은 이용자를 수용하면서 최소 비용을 발생시키는 차량 경로 조합을 설계하는 것을 목표로 한다. 이러한 DARP 문제는 노인이나 거동이 불편한 사람들을 위한 Door-to-Door 서비스 스케줄링을 비롯하여(Lehuédé et al., 2014), 오늘날에는 통합교통(Häll et al., 2008), 응급의료(Cappart et al., 2018), 승차공유(Çetin, 2017)와 같이 다양한 영역에서 다수의 이용자를 대상으로 단일 또는 다중 차량의 경로를 생성하는 데 적용되고 있다.

DARP는 경로 생성 과정에서 차량에 배차해야 할 수요를 모두 알고 있는지 여부에 따라 풀이 방식을 달리한다. 사전 예약 서비스와 같이 경로 생성 시 모든 수요를 미리 알고 있는 경우 정적 문제로 분류되며, 실시간 수요대응형 서비스와 같이 수요를 사전에 알 수 없어 경로를 미리 생성하지 못하는 경우 동적 문제로 구분된다. 본 연구의 대상인 다이나믹형 수요대응형 대중교통 서비스의 동적 경로 생성 문제는 후자에 해당하며, 기존 호출 수요를 서비스하면서 새로 발생한 호출을 실시간으로 차량 경로에 삽입하여 최적의 배차를 수행해야 한다. 선행 연구에서는 이러한 실시간 경로 배차를 위해 호출 우선순위에 따라 차량 경로에 호출을 삽입하는 삽입 휴리스틱 알고리즘이나, 일정 시간 또는 호출 수가 발생될 때까지 대기하다가 정적 배차를 반복적으로 수행하는 메타휴리스틱 알고리즘을 주로 활용해 왔다(Attanasio et al., 2004; Coslovich et al., 2006; Chassaing et al., 2016).

동적 DARP의 초기 모델은 Stein(1978)이 제시했으며, 이후 Psaraftis(1980)는 단일 차량을 대상으로 DARP의 정적 및 동적 버전 모두에 대한 동적 프로그래밍 알고리즘을 개발했다. Cordeau and Laporte(2007)는 용량, 이용자의 차내 이용시간, 차량 서비스 운영시간 등의 제약 조건을 적용하여 DARP 문제를 수리적으로 표현했으며, 이를 바탕으로 정적 문제와 동적 문제의 풀이 방식에 관한 선행 연구를 구분하였다. DARP 문제에 대한 선행 연구를 정리한 Table 1에 따르면 기존 연구에서는 차량의 경로 통행시간과 이동거리, 운영자의 비용을 기준으로 배차 최적화를 수행한 사례가 대부분이며, 이용자 관점의 서비스 지표를 경로 생성 알고리즘의 목적함수 또는 제약조건에 직접적으로 반영한 연구는 제한적이었다. 예를 들어, Desrosiers et al.(1986)은 모든 호출 수요의 승하차 요청을 미리 알고 있는 상황에서 용량 제약을 만족하면서 차량의 경로 통행시간을 최소화하는 DARP 경로 생성 알고리즘을 제시하였다. 또한, Cordeau and Laporte(2003)는 Tabu Search 알고리즘을 활용해 예약된 호출 수요를 기준으로 차량의 용량, 최대 경로 이동시간, 최대 차내 통행시간 제약 조건 아래 차량의 경로 이동거리를 최소화하는 DARP 경로 생성 알고리즘을 제안했다.

특히, 동적 DARP 문제에서 이용자 관점의 서비스 품질 지표를 반영한 연구는 드물었다. Wong et al.(2014)은 삽입 휴리스틱 알고리즘을 활용하여, 모든 호출 수요를 충족하기 위해 필요한 차량 수와 총 이동 거리를 최소화하는 동적 경로를 생성하면서, 이용자의 선호 시간대와 최대 주행시간에 대한 제약 조건을 추가하여 문제를 해결했습니다. Carotenuto and Martis(2017)는 다중 차량을 대상으로 하는 동적 DARP 문제를 두 단계로 구분하고, 삽입 휴리스틱 알고리즘을 통해 이용자의 승차 및 하차 요청 시간과 예정된 시간 간 차이를 최소화하는 방식으로 경로를 탐색하는 수요대응형 서비스 배차 방식을 제안하였다.

Table 1.

Previous studies on DARP routing and dispatch algorithms

Research	Objective	Time windows	Constraints	Algorithm	ProblemState
Psaraftis (1980)	Minimize route duration. Waiting time. Actual In-vehicle time	On pickup and delivery	Vehicle capacity Maximum position shift	Insertion heuristics. Dynamic programming	Dynamic DARP
Desrosiers et al. (1986)	Minimize route duration	On pickup and delivery	Vehicle capacity	Insertion heuristics. Dynamic programming	Static DARP
Cordeau and Laporte (2003)	Minimize total route length	On pickup and delivery	Vehicle capacity. Maximum route duration. Maximum in-vehicle time	Tabu search with vertex reinsertions	Static DARP
Ropke et al. (2007)	Minimize total route length	On pickup and delivery	Vehicle capacity. Maximum route duration. Maximum in-vehicle time	Branch-and-cut algorithm	Static DARP
Luo and Schonfeld (2011)	Minimize route duration Additional In-vehicle time	Time period Rolling Horizon	Vehicle capacity Maximum in-vehicle time	Rejected-reinserti on heuristics	Dynamic DARP
Wong et al. (2014)	Minimize the number of vehicles route duration	On pickup and delivery	Maximum ride time Time window of pickup time and delivery time	Insertion heuristics	Dynamic DARP
Carotenuto and Martis (2017)	Minimize customer delay	On pickup and delivery	Vehicle capacity Time window of pickup time and delivery time	Insertion heuristics	Dynamic DARP
Proposed	Maximize passenger utility	Time period. On pickup and delivery	Vehicle capacity Maximum waitingtime Maximum additional in-vehicle time	Insertion heuristics	Dynamic DARP

이와 같은 이용자 관점의 서비스 지표를 경로 생성 및 배차에 반영한 연구에서는, 이용자의 선호 요청 시간이나 추가 차내 시간에 스케일을 조정하기 위해 임의의 가중치를 곱하여 전체 목적 함수를 구성하거나, 제약조건을 추가하는 방식을 채택하는 경향이 있다. 한편, 수요대응형 대중교통 서비스에 대한 이용자의 선택 행동은 통행 시간을 구성하는 변수에 따라 서로 다른 효용을 가진다는 점이 밝혀진 바 있다(Lee et al., 2022; Youm et al., 2023). 이에, 본 연구에서는 대기시간, 차내 시간 등 통행시간 변수가 갖는 서로 다른 단위효용을 반영기 위하여 이용자의 효용 함수를 동적 경로 생성 알고리즘의 목적 함수에 직접 적용하여 경로를 생성하고, 시뮬레이션을 통해 그 효과를 차량 통행 시간 기반 배차와 비교하고자 한다.

동적 경로 생성 알고리즘 구성 및 이용자 효용 적용 방법

본 연구에서 제시하는 동적 경로 생성 구조는 다음 3가지 부분로 설명할 수 있다. 첫째, 동적 경로 생성은 호출 시간 순서에 따라 차량 경로에 승하차 노드를 추가하는 삽입 휴리스틱 알고리즘을 기반으로 매칭가능한 모든 경로를 생성한다. 이때, 차량 용량, 호출자 및 탐색 시점에서 서비스 이용 중인 승객의 1인당 최대 대기시간과 최대 추가 차내 시간을 제약 조건으로 고려하였다. 두 번째 부분은 이용자의 효용을 동적 배차 최적 경로에 적용하는 단계로, 각 호출에 대하여 비용함수 값이 가장 작은 경로를 매칭한다. 본 연구에서는 비용함수를 세 가지로 구성하였다. 먼저, 선행연구에서 주로 활용한 차량 경로 통행시간 비용함수를 구성하였다. 또한, 서비스 선택 시 이용자가 얻을 수 있는 효용을 로짓 모형을 활용하여 추정하고 이를 기반으로 이용자의 통행시간 효용 합을 최대화하는 경로를 매칭하도록 비용함수를 구성하였다. 마지막 부분에서는 효용 함수를 구성하기 위한 서비스 수락 모형 추정 단계에 대한 설명으로, 최적 경로 매칭에서 제시된 효용 함수를 구성하기 위한 방법을 소개한다. 이때, 활용된 자료는 경기도 화성시 남양뉴타운 일원을 대상으로 해당 서비스 실험선택 문항을 구성하고 잠재선호 설문을 수행한 결과를 활용하였다. 이를 토대로 효용최대화 이론 기반의 서비스 수락 로짓 모형을 추정하였으며, 모형의 계수 추정치를 활용하여 비용함수의 이용자 효용함수 부분을 구현하였다.

1. 동적 경로 생성 알고리즘

지난 10년 동안 많은 선행연구에서 DARP를 풀이하기 위하여 다양한 메타휴리스틱 알고리즘을 제안하였으나, 동적 DARP 문제의 경우 실시간 수요에 대하여 즉각적으로 실현 가능한 솔루션을 제시하기 위하여 삽입 휴리스틱 접근 방식을 주로 활용하고 있다(Ho et al., 2018). 삽입 휴리스틱 알고리즘은 Solomon(1987)이 제안한 알고리즘으로 승객의 노드를 순차적으로 기존 차량의 경로에 삽입하여 제약조건을 만족하는 동시에 탐색 시점에서 최적의 경로를 갱신하는 알고리즘이다. 이 알고리즘은 $n$ 개의 호출에 대하여 복잡도가 $O (n^{2})$ 로 실시간 호출 시점을 기준으로 빠른 경로 생성이 가능하다는 점에서 널리 활용되고 있다(Vallee et al., 2020). Table 2는 삽입 휴리스틱 알고리즘에 대한 일반화 코드를 나타낸다.

Table 2.

Procedures of generalized Solomon’s insertion Heuristic algorithm

1: Initialize empty route set
2: Select initial customer based on criteria (farthest from depot or earliest time window)
3: Create the first route with the selected customer
4: while there are unassigned customers do
5:        Select the next customer to insert based on criteria (cost of insertion, proximity to depot, etc.)
6:        best cost ← ∞
7:        best route ← None
8:        best position ← None
9:        for each route in current routes do
10:               for each position in route do
11:                 Calculate cost of inserting customer at this position
12:                    Check feasibility (capacity, duration, time windows)
13:                    if insertion is feasible (considering capacity, duration, time windows) and cost < best cost then
14:                    best cost ← cost
15:                    best route ← route
16:                    best position ← position
17:                 end if
18:            end for
19:        end for
20:        if best route̸ = None then
21:           Insert customer at best position in best route
22:           Update route accordingly
23:        else
24:           Create new route with selected customer
25:           end if
26: end while

본 연구에서는 다음 수요가 어떻게 발생할지 모르는 실시간 상황을 가정하고, 삽입 휴리스틱 알고리즘에 제약조건을 추가하여 동적 경로 배차 구조를 구성하였다. 동적 경로 생성에 있어서 차량의 위치는 탐색 시점(Period) $p$ 마다 갱신되며, 경로 갱신은 호출 발생에 따라 즉각적으로 승하차 노드를 운행 중인 차량 경로에 삽입하는 형태로 구현하였다. 이때, 호출 $p$ 를 수락하는 경우( $x_{k} = 1$ ), 탐색 시점 $p$ 에서 차량 $n$ 에 대한 경로 조합 $R (V | p, n, x_{k} = 1)$ 이 생성된다. 여기서, 경로 $r (r \in R)$ 은 호출자와 기존 이용객을 포함한 모든 승객 집합 $A$ 에 대하여 대기시간과 추가 차내 시간 제약조건을 만족한다. Equations 1, 2은 경로 $r (r \in R)$ 에 대한 승객 집합 $A$ 에 속하는 승객 $a$ 에 대한 최대 대기시간과 추가 차내 시간에 대한 제약조건을 수식화한 것이다.

(1)

t^{b a t c h} (a, r | p, n, x_{k} = 1) \leq t_{\max}^{b a t c h}

(2)

t^{a d d_{-} i v t} (a, r | p, n, x_{k} = 1) \leq t_{\max}^{a d d_{-} i v t}

또한, 새로운 호출 $k$ 를 수락함에 따라 경로 $r$ 의 모든 노드 $i$ 에 대하여 차량 $n$ 에 타고 있던 승객 수 $Q_{i n} (a, r)$ 에서 노드 $i$ 에서 하차하는 승객 수 $q_{i n} (a, r)$ 를 빼고 승차하는 승객 수 ${\hat{q}}_{i n} (a, r)$ 를 더한 값이 차량 용량을 넘어서지 않도록 제약조건을 구성하였다. 용량 제약을 수식으로 나타내면 Equation 3과 같다.

(3)

0 \leq (Q_{i n} (a, r) - q_{i n} (a, r) + {\hat{q}}_{i n} (a, r)) \leq Q_{\max}

이후 제약조건을 만족한 차량 $n$ 에 대한 경로 $r$ 은 지금까지 제약조건을 만족한 경로 중 최적으로 판별된 차량 $n$ 경로 $r$ 에 대하여 비용함수 값을 비교한 뒤 더 작은 비용함수 값을 나타내는 경로를 호출 $k$ 에 대한 최적 경로로 갱신한다. 다만, 모든 경로가 제약조건을 만족시킬 수 없는 경우 호출 불가를 반환하고 시뮬레이션 과정에서 이러한 호출 수요를 차량 배차 실패로 분류한다. Equation 4는 비용 함수를 활용한 최적경로 판별하는 수식을 나타낸다.

(4)

\min (C o s t (r | p), C o s t (r | p))

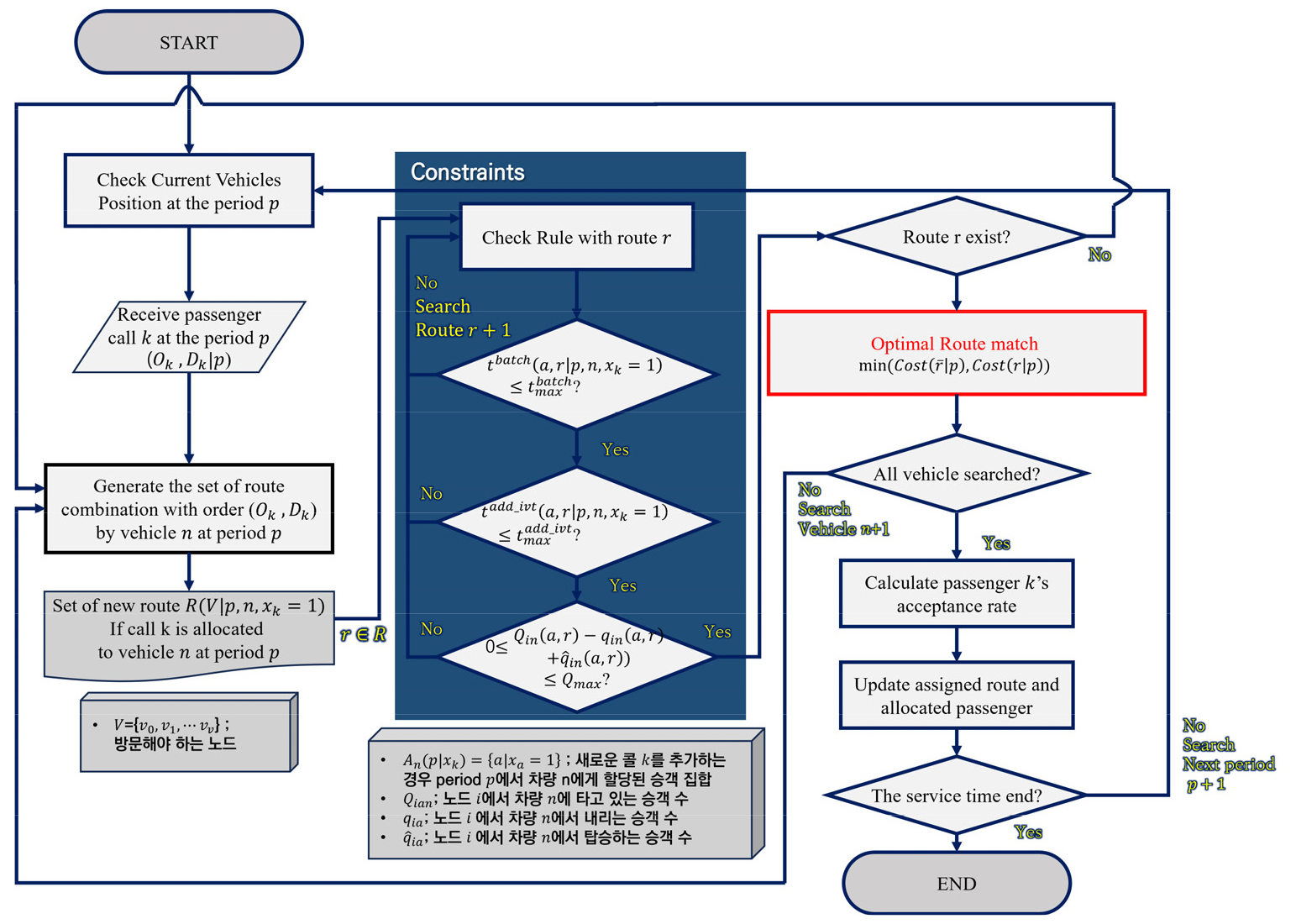
Figure 1은 동적 경로 생성 및 배차 알고리즘의 전반적인 경로탐색 과정을 나타낸 것으로 호출자와 앞서 차량에 배정된 승객 중 아직 탑승하지 않은 승객의 대기시간이 최대 대기시간을 충족하는지 여부를 비롯하여 앞서 배정된 승객 중 차량에 탑승 중인 승객의 차내 통행시간이 최대 추가 차내 시간 조건을 만족하는지 순차적으로 탐색하는 구조를 나타낸다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-06/N0210420606/images/kst_2024_426_706_F1.jpg

Figure 1.

The process of dynamic route generation using an insertion Heuristic algorithm

2. 이용자 효용을 반영한 동적 배차 비용함수

본 연구에서는 선행연구에서 주로 활용하고 있는 차량 경로 통행시간을 기반으로 한 비용함수를 비롯하여 이용자 효용을 반영한 비용함수, 그리고 두 함수를 선형으로 결합한 세 가지 형태의 비용함수를 비교하였다. Equation 5는 차량 경로 통행시간에 대한 비용함수를 수식으로 나타낸 것으로 경로 $r$ 에 대하여 인덱스 함수 $I_{i j n} (r)$ 와 링크별 통행시간 $c_{i j n}$ 의 가중합으로 구성된다. 이때, 인덱스 함수 $I_{i j n} (r)$ 는 경로 $r$ 에 노드 $i$ 에서 노드 $j$ 로 진행하는 방향의 링크 $l_{i j}$ 를 포함하는 경우 1 그렇지 않은 경우 0 값을 갖는다. 수식으로 나타내면 Equation 6와 같다.

(5)

C o s t_{1} (r | p) = \sum_{n \in N} \sum_{j \in V} \sum_{i \in V} c_{i j n} I_{i j n} (r | p)

(6)

I_{i j n} (r) = \{\begin{cases} 0 & if l_{i j} \in r \\ 1 & o t h e r w i s e \end{cases}

다음으로 이용자 효용을 반영한 비용함수는 수요대응형 서비스 통행시간을 구성하는 네 가지 변수(접근시간, 대기시간, 차내 시간, 하차 후 소요시간)에 대하여 서비스 선택 시 이용자가 얻을 수 있는 관측 효용 합에 대한 역수를 활용하였다. 통행시간으로 구성된 서비스 선택 시 이용자가 얻는 관측 효용은 통행시간 변수의 값이 커질수록 음의 효용을 갖는다. 여기서 효용의 절대값은 선행연구에서 제시한 이용자 대기시간과 차내 시간에 대한 가중합과 수식적으로 동일하다. 다만, 선행연구에서 제시한 대기시간과 차내 시간에 대한 가중합은 패널티 관점의 지표라면, 효용이 클수록 이용자가 선호하는 경로를 의미한다. 또한, 본 연구에서 제시한 비용함수는 이용자 통행시간에 대한 가중치를 적용함에 있어 서비스 운영자가 결정한 임의의 가중치가 아닌 효용 최대화 이론에 기반하여 이용자의 선택행위를 추정한 모형의 결과물이라는 점에서 차별점이 있다. 이에 본 연구에서는 모든 차량 $n$ 의 경로 $r$ 에 대하여 승객 집합 $A$ 가 얻을 수 있는 효용의 합을 활용하되 차량 경로 통행시간을 기반으로 구성된 비용 최소화 탐색 구조와 연결성을 고려하여 이용자 효용 합의 역수를 비용 함수로 구성하였다. Equation 7는 이용자 효용을 반영한 비용함수를 나타내며, Equation 8은 수요대응형 대중교통 서비스 수락 시 경로 $r$ 의 통행시간 변수에 따라 이용자가 얻을 수 있는 관측 효용을 나타낸다.

(7)

C o s t_{2} (r | p) = (\sum_{n \in N} \sum_{a \in A} V_{D R T} (a, r | p))^{- 1}

(8)

V_{D R T} (a, r | p) = β_{D R T}^{T} X_{D R T}^{T} (a, r | p)

마지막으로 본 연구에서는 이용자의 효용과 차량 경로 통행시간에 대한 비용함수 두 가지 형태를 선형 결합한 비용함수를 제시한다. 여기서, 차량의 경로 통행시간은 운영자의 운영비용을 대리할 수 있다는 점에서 운영자 관점의 목적함수라고 간주할 수 있다. 한편, 이용자 효용합의 역수는 승객의 관점에서 경로를 갱신하는 경우 이용자가 격게되는 효용을 나타낸다. 따라서, 두 목적함수의 선형결합을 통해 서비스를 구성하는 운영자와 이용자 두 이해관계자의 비용을 동적 경로 생성에 동시에 반영할 수 있다. 이를 수식으로 나타내면 Equation 9와 같다. 다만, 두 비용함수의 스케일이 다르다는 점에서 최적의 지표 결합을 탐색하기 위하여 가중치 $λ$ 를 적용하였다. 자세한 설명은 제4장과 5장에서 다루고 있다.

(9)

C o s t_{3} (r | p) = C o s t_{1} (r | p) + C o s t_{2} (r | p)

3. 이용자 잠재선호 설문조사 및 서비스 수락률 모형 구성

본 연구에서는 이용자의 효용을 경로 배차 알고리즘에 반영하기 위하여 시뮬레이션 대상지에 해당하는 경기도 화성시 남양뉴타운 일원의 13세 이상 실제 거주자 및 종사자 500명을 대상으로 잠재선호 설문조사를 수행하였다. 표본의 대표성을 확보하기 위하여 시뮬레이션 수행 대상지와 동일한 지역단위의 거주 및 종사자 인구 수를 고려하였다. 모집단은 조사지 내 거주지 호수의 3배와 상업 시설 수의 1.5배 합으로 설정하였으며, 표본 수는 모집단의 약 1%에 해당하는 규모로 구성하였다. 설문 기간은 2024년 6월 24일부터 7월 12일 약 3주간 진행되었다. Table 3는 설문 응답자 사회경제적 속성에 대한 기초통계를 나타낸다. 주요 항목별 응답자 분포를 살펴보면, 거주 및 근무에 있어 설문 지역 내 거주만 하는 응답자는 81.2%, 근무만 하는 응답자는 3.8%, 거주와 근무를 모두 하는 응답자는 15.0%로 나타났다. 성별은 남성이 50.4%, 여성이 49.6%로 성비가 균등하게 나타났다. 연령대는 20-29세가 10.2%, 30-39세가 24.2%, 40-49세가 20.2% 등 다양한 연령대가 포함되었다. 소득 분포에서는 월 소득 3-5백만 원과 5-10백만 원 구간에 응답자가 각각 33.0%와 33.8%로 집중되어 있다. 고용 상태는 재직자가 55.6%, 비재직자가 44.4%로 조사되었다. 운전면허는 응답자의 72.6%가 보유하고 있으며, 43.2%는 본인 소유 차량을 보유하는 것으로 나타났다.

Table 3.

List for Socio-demographic variable of sample (N=500)

Variable	Category	Frequnecy
Residence & empolyment	Only residence within survey area	406(81.2%)
	Only Employment within survey area	19(3.8%)
	Residence and employment within survey area	75(15.0%)
Gender	Male	252(50.4%)
Gender	Female	248(49.6%)
Age	under 20 years old	58(11.6%)
	20-29 years old	51(10.2%)
	30-39 years old	121(24.2%)
	40-49 years old	101(20.2%)
	50-59 years old	85(17.5%)
	More than 60 years old	84(16.8%)
Income	Less than 1 million KRW per month	18(3.6%)
	1-2 million KRW per month	23(4.6%)
	2-3 million KRW per month	45(9.0%)
	3-5 million KRW per month	165(33.0%)
	5-10 million KRW per month	169(33.8%)
	More than 10 million KRW per month	16(3.2%)
	Response Refusal	64(12.8%)
Employment status	Employed	278(55.6%)
Employment status	Unemployed	222(44.4%)
Driving license	Acquired	363(72.6%)
Driving license	Not Acquired	137(27.4%)
Car ownership	Self-owned	216(43.2%)
	Family-owned	183(36.6%)
	None	101(20.2%)

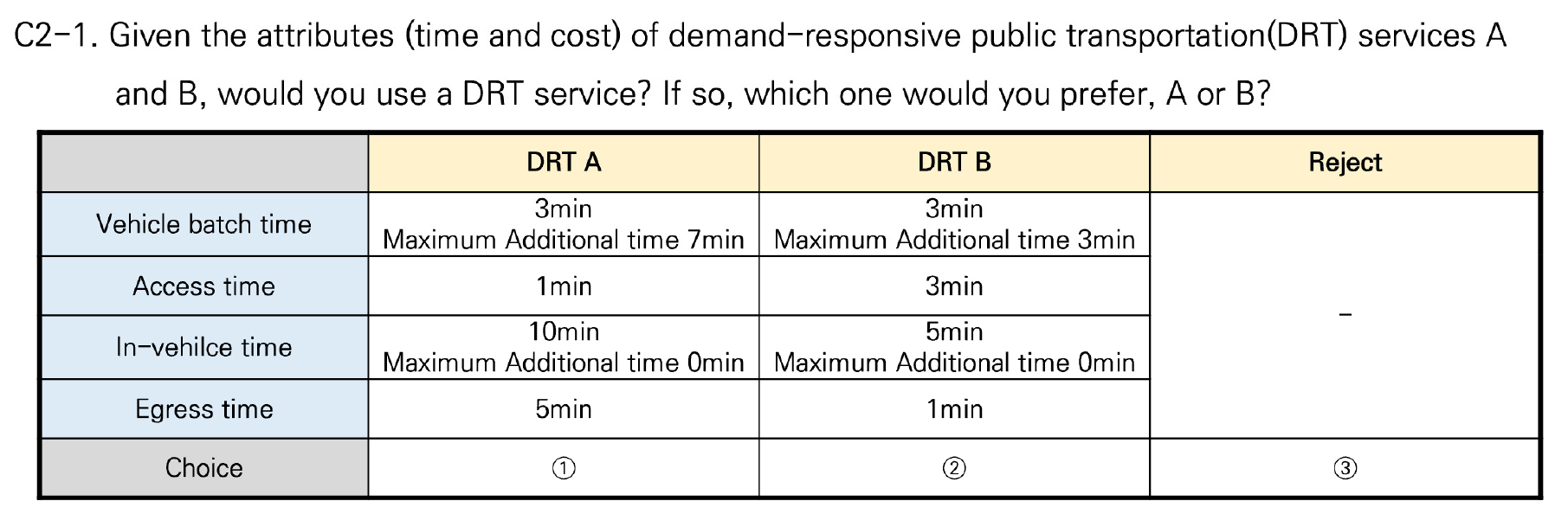
잠재선호 설문은 리빙랩 지역 내 서비스가 도입된 경우를 가정하고 서비스 대안 2가지와 거절 대안 1가지로 구성된 선택실험을 구성하였다. 승차지점까지 도보 접근시간, 승차지점까지 차량 접근시간(최소), 차내 시간(최소), 하차 후 소요시간을 비롯하여 수요대응형 대중교통 서비스의 불확실 요인을 반영하기 위하여 승차지점까지 차량 접근 추가시간과 차내 통행 추가시간을 포함하여 서비스 대안을 구성하는 6가지 통행시간 변수를 구성하고 3가지 수준으로 구분하였다. 또한, 차량이 먼저 도착하여 이용자를 기다리는 상황을 제외하기 위하여 도보 접근시간이 차량 접근시간(최소)보다 작도록 제약조건을 추가하기 위하여 D-error를 최소화하는 Efficient Design 방법을 활용하여 대안별 통행시간 조합을 설계하였다. 이때, 활용한 기반 모형은 Youm et al.(2023)의 설문결과를 토대로 초기 효용함수를 구성하였다. 문항 설계는 Ngene 소프트웨어에서 제공하는 Cook and Nachtsheim(1980)의 수정된 Federov 알고리즘를 이용하여 상관성을 최소화하는 방향으로 9개 Block을 분할하고, 1인당 6가지의 가상 시나리오에 응답 수행하도록 설문을 구성하였다. 총 4,255,829번의 무작위 시행 횟수를 거쳤으며, 그 결과 D-error 0.0196, A-error 0.0259의 설문설계 결과를 토대로 문항을 구성하였다. Table 4는 서비스 대안의 변수별 속성 구분을 나타낸다. 단, 차량 접근 추가시간과 차내 통행 추가시간은 차량 접근시간 및 차내 시간과 구분되어 응답자에게 제시되었다. Figure 2는 설문문항 예시를 나타낸다.

Table 4.

Level of attritbute

Attribute	Level
Vehicle batch time (minimum)	3 min	5 min	7 min
Additional vehicle batch time	+ 3 min	+ 5 min	+ 7 min
Access time	1 min	3 min	5 min
In-vehicle time (minimum)	5 min	10 min	15 min
Additional in-vehicle time	+ 0 min	+ 5 min	+ 10 min
Egress time	1 min	3 min	5 min

https://cdn.apub.kr/journalsite/sites/kst/2024-042-06/N0210420606/images/kst_2024_426_706_F2.jpg

Figure 2.

The Example of state preference survey for DRT service acceptance (Translated in English)

수요대응형 서비스 대안 수락 모형은 통행자 행태연구에서 전통적으로 활용하고 있는 효용극대화 이론 기반의 혼합 로짓 모형을 활용하였다. 수요대응형 대중교통 서비스 수락 시 효용함수는 통행시간 변수를 활용하여 관측 효용부분을 구성하였으며, 거절 대안은 응답자의 사회경제적 속성을 반영하였다. 단, 응답자 1인당 6번의 응답을 반복 수행하였다는 점에서 반복 응답에 따른 비관측 요인의 영향을 반영하기 위하여 거절 대안 오차항 $ε_{N o, k t}$ 에 패널효과항 $α_{N o, k}$ 을 추가하였다. 패널효과는 응답자 $k$ 에 대한 표준 정규분포 $α_{N o, k} ~ N (0, σ_{α_{N o}})$ 를 따른다고 가정하였다. Equations 10, 11은 서비스 수락과 거절 대안에 대한 효용함수를 나타낸다.

여기서 $X_{D R T, k t}^{T}$ 는 각 설문 사황에서 대안별 통행시간 정보(접근시간, 대기시간, 추가 대기시간, 차내 시간, 추가 차내 시간, 하차 후 소요시간)를 나타낸다. 이때, 대기시간은 차량 배차시간에서 접근시간을 뺀 값으로 산정하였다. 또한, $X_{k}^{Z}$ 는 응답자 $k$ 에 대한 6가지 사회경제적 속성(연령, 성별, 고용 상태, 면허 유무, 본인 차량 보유 여부, 저소득 가구 유무)을 변수로 채택하였다. 소득 속성은 2024년 대한민국 2인가구 중위소득이 368만 2,609원/월 이라는 점을 고려하여 월 평균 가구소득이 300만원 미만인 가구를 저소득 가구로 더미화했다.

(10)

U_{D R T, k t} = β_{D R T}^{T} X_{D R T, k t}^{T} + ε_{D R T, k}

(11)

U_{N o} = β_{0} + β^{Z} X_{k}^{Z} + ε_{N o, k t}

혼합 로짓 모형은 선택상황 $t$ 에서 개인 $k$ 가 대안 $i$ 를 선택할 확률 $P_{i k t}$ 이 확률밀도함수 $f (α_{i k})$ 를 따른다고 가정하여 추정한다. Equation 12는 대안 선택확률 $P_{i k t}$ 의 적분 형태를 나타낸다. 한편, 표준정규분포와 같이 닫힌형태가 아닌 확률밀도함수를 가정하는 경우 수리적으로 추정이 불가능하기 때문에 Halton draw방식을 활용한 시그마 합 형태로 근사한 시뮬레이션 기반 로그 우도함수를 활용하여 모형을 추정한다. Equation 13은 시뮬레이션 기반 로그 우도함수를 나타낸다.

(12)

P_{i k t} = \int_{α_{i k}} \frac{\exp (V_{i k t} + α_{i k})}{\sum_{j \in J} \exp (V_{j k t} + α_{i k})} f (α_{i k} | 0, σ_{α_{i}}) d α_{i k}

(13)

S L L = \frac{1}{R} \sum_{r = 1}^{R} \sum_{j = 1}^{J} \sum_{k = 1}^{K} \sum_{t = 1}^{T} d_{k j t} \ln (\frac{\exp (V_{j k t} + α_{j k}^{r})}{\sum_{j \in J} \exp (V_{j k t} + α_{j k}^{r})})

시뮬레이션 실험

1. 시뮬레이션 실험 설계

Table 5는 시뮬레이션에 적용된 하이퍼 파라미터를 나타낸다. 먼저, 서비스 배차 시 사용할 수 있는 차량의 수와 용량을 나타내는 수용 용량(Capacity)은 운전자 좌석 1석을 제외한 14석으로 설정하였으며, 차량 대수는 5대로 가정하였다. 차량 속도(Vehicle speed)는 20km/h로 설정하였고, 승하차지에서 소요되는 점유 시간(dwelling time)은 30초로 적용하였다. 시뮬레이션 실험에서는 최대 대기시간과 최대 추가 차내 시간을 5분에서 99분까지 변화시키며 제약조건을 테스트하였다. 최대 대기시간을 조정할 경우 최대 추가 차내 시간은 60분으로 고정하였고, 최대 추가 차내 시간을 조정할 경우 최대 대기시간은 동일하게 60분으로 고정하였다. 또한, 운영자 관점의 차량 경로 통행시간과 이용자 관점의 효용을 결합한 비용함수에서는 두 지표값 간의 trade-off를 확인하고자 가중치(Scaling weight)에 따른 시뮬레이션 실험을 수행하였다. 가중치는 1부터 10⁶까지 10의 배수 값을 적용하여 비교하였다. 한편, 제약조건 비교 실험에서는 비용함수의 가중치를 1로 고정하였으며, 최적 가중치 탐색 실험에서는 통행시간 제약조건을 모두 10분으로 설정하고 분석을 진행하였다.

Table 5.

Hyperparameter of simulation

Hyperparameter		Value
Fixed	Capacity	14 seats/veh, 5 vehicle
	Vehicle speed	20km/h
	Dwelling time	30 sec
	Real time demand	Total 366 calls
	Operating time	A.M 7~10
Variable	Maximum waiting time	5~99 min, default 60
	Maximum additional in-vehicle time	5~99 min, default 60
	Scaling weight	1, 10, 10², 10³, 10⁴, 10⁵, 10⁶, defualt 1

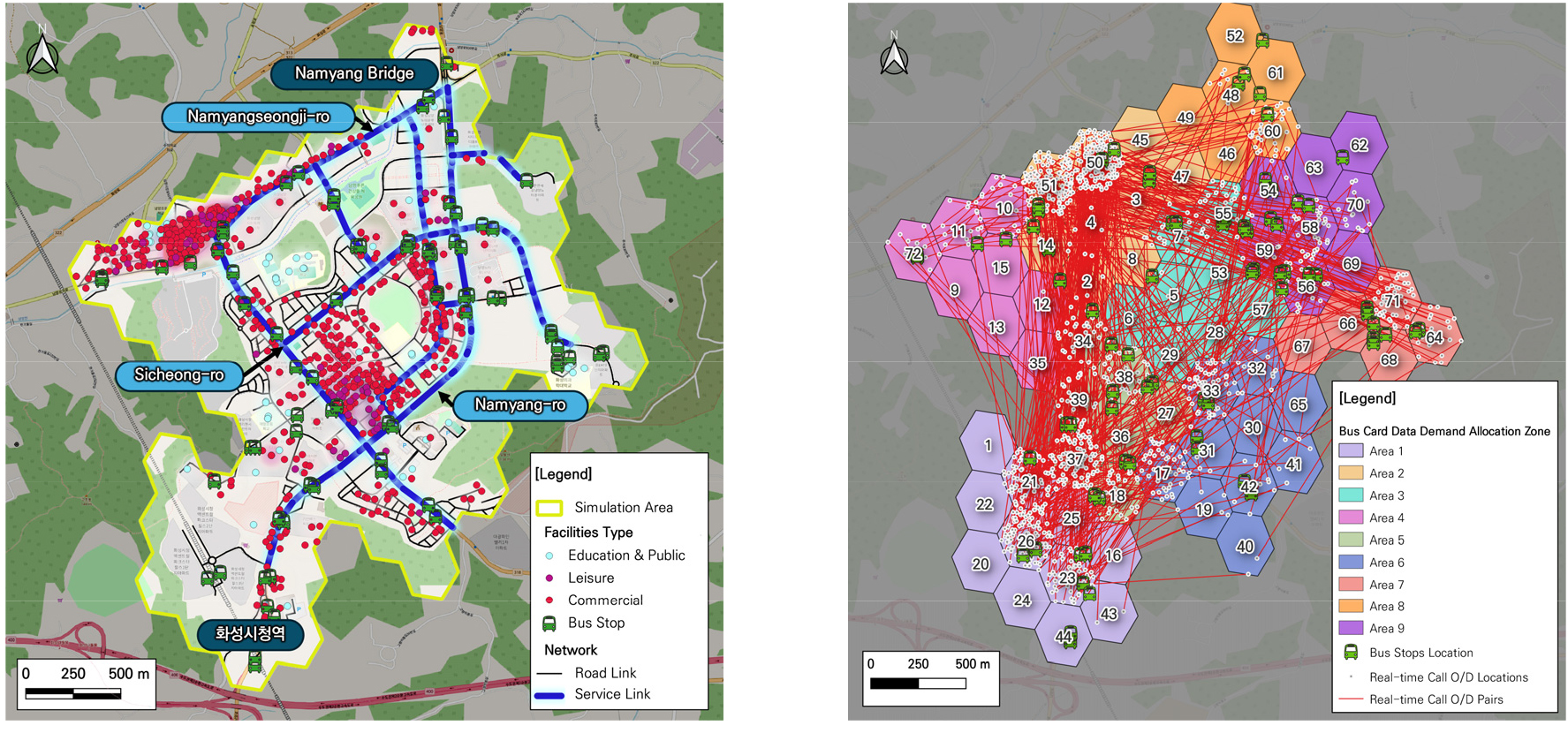
시뮬레이션 환경은 실시간 수요대응형 자율주행 대중교통 모빌리티 서비스 기술 개발 연구가 진행 중인 경기도 화성시 남양뉴타운 일원을 중심으로 구현되었다. 본 시뮬레이션 대상지는 시청로와 남양로, 남양성지로를 경계로 둘러싸여 있으며, 역골중앙로와 남양중앙로가 대상지 중앙을 세 가지 구역으로 구분하고 있다. 시설물 분포를 살펴보면 남양성지로를 기준으로 좌측 상단과 시청로와 남양로를 기준으로 화성시청 인근 우측 하단영역에 상업시설 및 여가시설이 집중적으로 분포되어 있으며, 이면도로 인근 교육 및 공공기관이 분포하고 있다. 특히, 남양중학교와 남양고등학교, 신백중학교가 위치한 이면도로에 대하여 어린이보호구역이 설정되어 있기에 대중교통 서비스의 승하차 발생을 고려하여 차량 운행가능 경로는 왕복 4차로 이상의 도로 및 지선 일부로 한정하였다. 한편, 본 대상지의 우측 상단에 위치한 남양교에서 좌측 하단에 위치한 화성시청역까지 승용차를 기준으로 약 15분 내 통행이 가능한다. Figure 3의 좌측영역에 해당하는 그림은 본 시뮬레이션 대상지의 도로 및 시설물 분포 현황을 나타낸다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-06/N0210420606/images/kst_2024_426_706_F3.jpg

Figure 3.

Simulation target area network (left), bus stops and real time demand locations (right)

본 연구의 수요대응형 대중교통은 Door-to-door 서비스를 지향하므로 시뮬레이션 대상지를 Uber의 H3 육각격자를 활용하여 해상도 9의 72개 격자로 구분한 뒤 실시간 수요와 승하차 발생을 대상지 영역으로 한정하였다. 2023년 기준 대상지 육각격자 내에는 총 75개의 버스 정류장이 위치하고 있으며, 총 52개 버스 노선이 대상지 내 주요 도로에 해당하는 시청로, 남양로 등을 따라 통과하는 것으로 나타났다. 본 연구에서는 한국교통안전공단에서 제공하는 대중교통 카드데이터를 토대로 2023년 9월 6일 수요일 시뮬레이션 대상지 내 승하차가 발생한 카드내역을 추출하여 실시간 호출 수요를 구성하였다. 대중교통 카드데이터 내역에 따르면 본 시뮬레이션 대상지 내 승하차 위치를 식별가능한 통행량이 오전 7시부터 오후 23시까지 2,016통행/일로 나타났으며, 그 중에서 시청로를 중심으로 가로변에 위치한 버스 정류장에서 상대적으로 승하차가 많이 발생하는 것으로 나타났다.

한편, 버스 정류장 승하차 내역은 최종 기종점(O/D) 위치를 알 수 없다는 점에서, 72개 육각격자 영역을 다시 버스정류장을 기준으로 9개 구역으로 구분하고 개별 격자에 위치한 주거용 건물의 가구호수 및 상업용 건물의 점포 수를 집계하여 그룹별 비중에 맞추어 버스 통행량을 배분하였다. 이때, 활용된 버스 통행량은 대중교통 카드데이터의 평균 에 대한 포아송 분포를 따른다고 가정하였으며, 그 결과 실시간 호출 수요(Real time demand)는 3시간 동안 366명을 포함하는 것으로 나타났다. Figure 3의 우측 그림은 시뮬레이션에 활용된 실시간 호출 수요를 나타낸다.

본 시뮬레이션 실험 결과를 비교하기 위하여 효과 지표를 다음과 같이 구성하였다. 먼저, 차량 거리당 서비스 인원을 의미하는 운영자 관점 지표(Operator perspective index)를 활용하여 서비스 효율을 비교하고자 하였다. 여기서 차량 거리는 운영자가 서비스를 제공하면서 발생하는 비용을 대리하며, 차량 거리 대비 서비스 인원이 많을수록 운영자가 제공하는 교통 서비스의 효율성이 높음을 의미한다. 다음으로 이용자 관점 지표(User perspective index)를 의미하는 이용자 평균 총 통행시간 대비 총 지연시간을 집계하여 비용함수에 따라 개별 시뮬레이션 상황에서 이용자 관점의 서비스 효율을 비교하고자 하였다. 마지막을 본 연구에서는 차량의 배차 실패를 제외하고 이용자의 서비스 수락 거절을 시뮬레이션 상 구현하지 않았으나, 실제 서비스 환경에서는 이용자의 서비스 거절이 발생할 수 있다. 따라서, 비용함수에 따른 배차 서비스 성능을 비교하기 위하여 배차 성공횟수 대비 잠재선호 수락 모형에 따른 이용자의 수락 여부를 공급 대비 실 수요 지표(Demand supply index)로 구성하고 비교하고자 하였다. 서비스 수락여부는 이용자 잠재선호 서비스 수락 모형을 활용하여 차량 배차에 성공한 호출자가 차량 승차 직전까지 제공받은 통행정보를 토대로 서비스 수락 확률을 계산한 뒤 50%의 확률을 넘는 경우 서비스 수락 의지가 있다고 판별하였다. Table 6는 본 시뮬레이션 실험 효과 평가 지표를 나타낸다.

Table 6.

Performance metrics

Metrics	Description
Operator perspective index	Passengers served per vehicle distance
User perspective index	Average rate of delay time relative to total travel time per user
Demand supply index	Rate of user acceptance based on potential preference acceptance model relative to successful dispatch attempts

2. 이용자 효용함수 추정 및 시뮬레이션 반영

Table 7는 잠재선호 설문결과를 토대로 시뮬레이션 대상지 내 수요대응형 대중교통 서비스 도입시 서비스 수락 여부에 대한 모형 추정 결과를 정리한 것이다. 모형은 Econometric Software 사의 Nlogit 5를 활용하여 추정하였으며, 2000번의 Halton draw를 시행하도록 설정하였다. Model 1은 추가 대기시간과 추가 차내 통행시간을 구분하지 않고 최대 대기시간과 최대 차내 통행시간으로 설명 변수를 구성한 혼합 로짓 모형의 결과를 나타내며, Model 2는 추가 대기시간과 추가 차내 시간을 구분한 혼합 로짓 모형 추정 결과를 나타낸다.

Table 7.

The results of mixed logit model estimation

Attribute		Model 1				Model 2
Attribute		Coefficient		Std.	p-value	Coefficient		Std.	p-value
Alternative specific constant		-12.585	***	1.688	<0.001	-14.439	***	1.773	<0.001
Alternative attributes $X_{D R T, k t}^{T}$	Access time	-0.165	***	0.018	<0.001	-0.307	***	0.024	<0.001
	Waiting time					-0.179	***	0.020	<0.001
	Additional waiting time					0.013		0.016	0.417
	Maxium waiting time	-0.029	***	0.011	0.009
	In-vehicle time					-0.217	***	0.009	<0.001
	Additional in-vehicle time					0.010		0.007	0.146
	Maxium in-vehilcle time	-0.070	***	0.005	<0.001
	Egress time	-0.243	***	0.014	<0.001	-0.250	***	0.017	<0.001
Socio -demographic $X_{k}^{Z}$	Age	0.050	*	0.028	0.074	0.054	*	0.030	0.069
	Gender (male =1)	-1.323		0.919	0.150	-1.387		0.965	0.151
	License (acquired=1)	2.859	**	1.207	0.018	3.009	**	1.265	0.017
	Low income (less than 3 million KRW per month)	2.732	**	1.213	0.024	2.871	**	1.272	0.024
	Car ownership (self-owned=1)	2.612	**	1.035	0.012	2.750	**	1.087	0.011
	Employment status	-1.339		0.987	0.175	-1.451		1.037	0.162
Standard deviation of panel effect		6.624	***	0.702	<0.001	6.955	***	0.735	<0.001
Goodness of fit	Number of observation	9,000				9,000
	Number of draw	2,000				2,000
	$L L (0)$	-3295.84				-3295.84
	$L L (β)$	-2105.90				-1798.21
	$ρ^{2}$	0.361				0.454
	Adjusted $ρ^{2}$	0.358				0.452

note: *Significance Level<0.1, **Significance Level<0.05, ***Significance Level<0.01

모형 추정 결과 Model 1과 Model 2의 자유도가 각각 12과 14인 반면, adjusted $ρ^{2}$ 가 0.361, 0.452로 나타났다. 따라서, 대기시간과 차내 통행시간의 변수에 대하여 추가시간을 구분할 필요가 없음을 귀무가설로 하는 제약모형 Model1과 추가시간에 대한 범위를 독립적인 변수로 구분한 Model2에 대하여 log-likelihood 값을 활용하여 카이제곱 검정을 수행한 결과 자유도 차이 2에 대하여 카이제곱 값 $χ^{2}$ 이 615.37으로 99.0%의 신뢰수준 범위에서 Model 2가 통계적으로 유의미한 모형임을 파악하였다. 이에 본 연구에서는 Model 2를 최종 모형으로 선택하였다. Model 2의 추정결과를 살펴 보면 접근시간, 대기시간, 차내 시간, 하차 후 소요시간 모두 통계적으로 유의미한 음의 계수를 갖는 것으로 나타난 반면, 추가 대기시간과, 추가 차내 시간은 유의하지 않는 것으로 나타났다. 이러한 결과는 시뮬레이션 대상지와 같이 작은 규모의 환경에서는 수요대응형 대중교통 서비스를 제공함에 있어서 선제적으로 미래에 발생가능한 추가 대기시간과 추가 차내 시간 범위를 제시하는 것이 유의미한 통행정보가 아님을 나타낸다. 따라서, 본 연구에서는 시뮬레이션 모형 내 효용함수를 반영함에 있어 추가 대기시간과 추가 차내 시간 발생가능 범위를 반영하지 않았다. 또한, 호출자의 승차 직전까지 배차 정보를 토대로 수락률을 산정하는 과정에서 역시 두 조건을 고려하지 않았다.

한편, 거절 대안의 설명변수로 투입한 6가지 사회경제적 속성에 대한 Model 2 추정치를 확인해본 결과 성별과 고용 상태는 통계적 유의성을 만족하지 않는 것으로 나타났으나, 연령이 높을수록, 저소득 가구에 속할수록, 면허 또는 본인 차량을 보유하는 경우 서비스 대안을 거절할 확률이 더 높음을 파악하였다. 본 연구에서는 시뮬레이션 실시간 호출 수요 당 서비스 수락를 판별함에 있어 설문 응답의 평균 사회경제적 속성을 반영했다.

실험 결과

시뮬레이션 실험은 Intel(R) Core(TM) i9-9900 CPU, RAM 64GB, NVDIA GeForce GTX 1660 Ti의 로컬 pc에서 Python 3.10.11 환경을 활용하여 수행하였다. 최대 대기시간과 최대 추가 차내 시간 제약조건의 하이퍼 파라미터를 5부터 99까지 변화시켜가면서 실험을 수행하여 총 190번 시뮬레이션을 반복하였다. 그 결과 차량 경로 통행시간 비용함수 기반 시뮬레이션은 주어진 366명에 대한 실시간 호출 수요를 모두 처리하는데 시뮬레이션 1회 당 평균 340.40초가 소요되었으며, 효용함수 역수 비용함수 기반 시뮬레이션은 412.86초, 차량 경로 통행시간과 효용함수 역수를 선형 결합한 비용함수의 경우 480.84초 소요되었다.

1. 최대 대기시간 변수 실험 결과

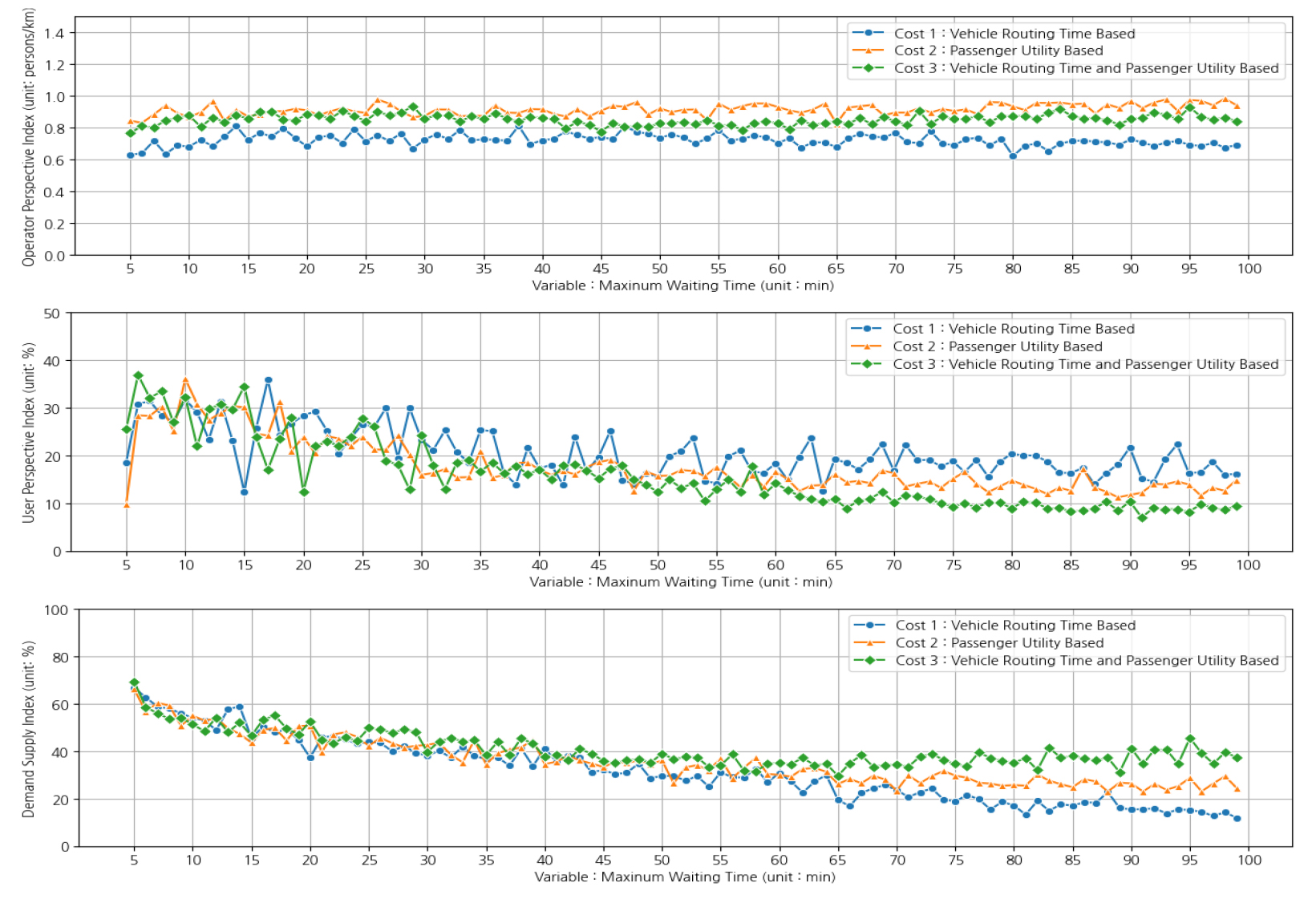
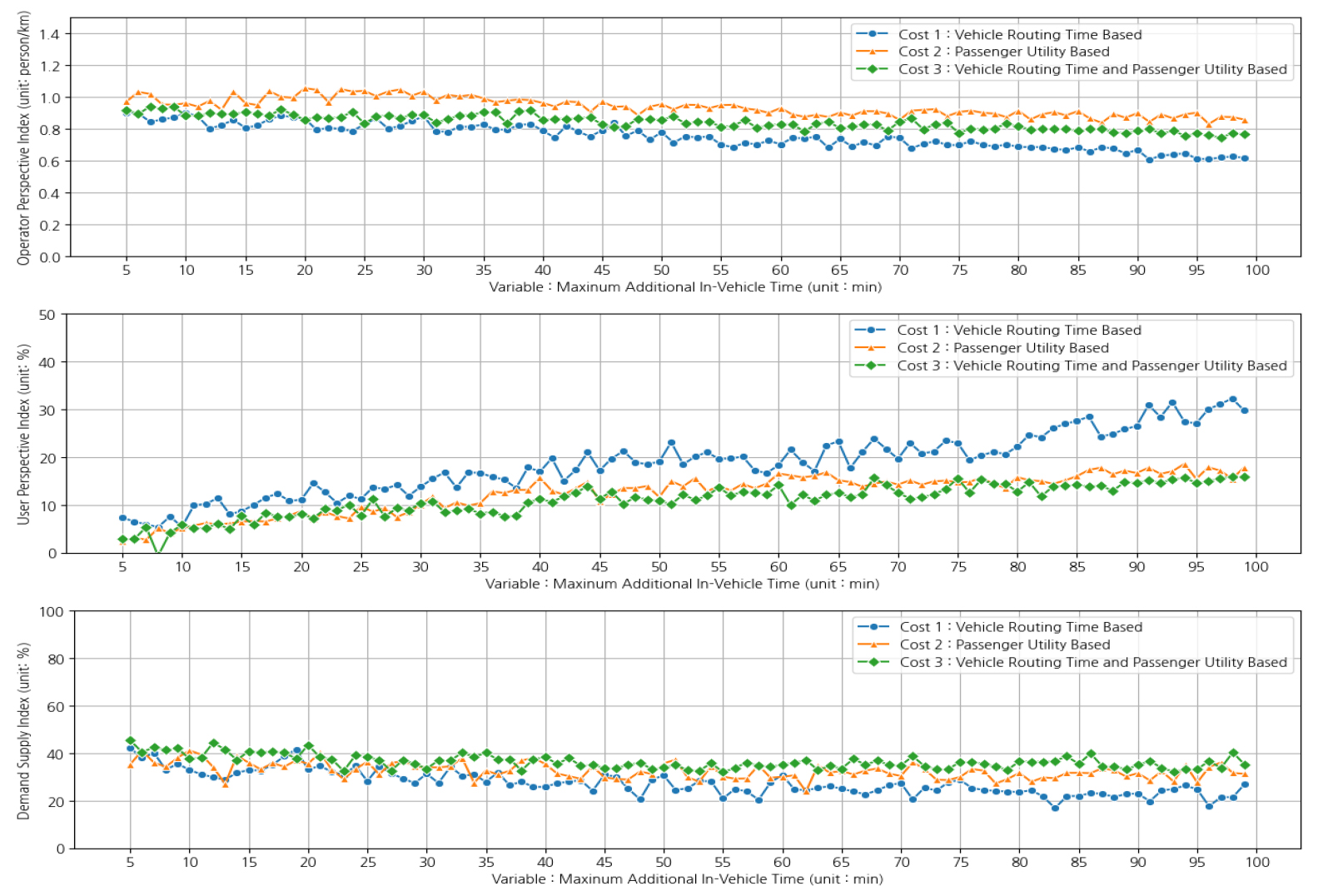
Figure 4는 수요대응형 서비스에서 대기시간 제약조건을 변경하면서 차량 배차 시뮬레이션을 수행한 결과를 나타낸다. 첫 번째 그래프는 운영자 관점 지표(Operator perspective index)에 대한 결과로, 차량 통행 거리 대비 서비스 인원(명/km)의 변화를 보여준다. 그래프에 따르면, 대기시간 제약조건을 완화하여도 서비스 인원의 비율은 전반적으로 안정적인 수준을 유지하는 경향이 있다. 차량 경로 통행시간 기반 비용함수 결과와 차량 경로 통행시간 및 이용자 효용을 결합한 비용함수를 적용한 결과가 유시한 수치를 보였다. 한편, 본 시뮬레이션 실험 결과에서는 이용자 효용 기반 비용함수에 대한 결과물이 다른 두 비용함수 옵션에 비하여 상대적으로 더 높은 수치를 기록하고 있다. 이러한 결과는 오히려 시뮬레이션 환경과 같이 행정동 단위보다 작은 영역에서 수요대응형 서비스를 운행하는 경우 차량 경로 통행시간보다 지연시간을 보수적으로 판단하는 이용자 효용 기반 배차 전략이 운영자 관점에서 더 효율적일 수 있음을 나타낸다.

두 번째 그래프는 이용자 관점 지표(User perspective index)로, 총 통행시간 대비 지연시간 평균 비중(%)을 나타낸다. 차량 경로 통행시간 기반 비용함수을 적용하는 경우가 이용자 효용을 기반으로 배차를 수행하는 경우보다 대기시간 제약조건에 따라 지연시간의 비중 격차가 더 크게 나타났다. 또한, 대기시간이 제약조건을 완화할수록 지연시간의 비율이 점차 감소하는 추세를 보였다. 이는 대기시간 제약조건을 완화할수록 이용자에게 제공된 초기 통행시간 조건 자체가 매우 긴 대기시간을 요구하는 형태를 보인다는 점에서 상충관계가 있다. 그래프 비교결과에 따르면 차량 경로 통행시간 기반 배차보다 이용자 효용을 반영하여 서비스 배차를 수행하는 것이 이용자 관점에서 신뢰성을 서비스의 신뢰성 감소를 완화하는 효과가 있다.

한편, 세 번째 그래프는 공급 대비 실 수요 지표(Demand supply index)에 대한 결과물로, 차량 배차 성공 횟수 대비 잠재선호 모형에 따른 이용자 서비스 수락 비율(%)을 나타낸다. 이 그래프에서는 대기시간이 증가할수록 이용자 수락 비율이 점진적으로 감소하는 경향이 있다. 대기시간 제약조건이 짧을 때는 이용자 서비스 지표와 유사하게 세 비용함수의 차이가 두드러지지 않았으나, 60분 이상의 대기시간 제약조건 아래에서 차량 경로 통행시간과 이용자의 효용을 모두 고려한 비용함수가 상대적으로 높은 퍼포먼스를 보였다. 다만, 본 실험에서는 최대 추가 차내 시간을 60분으로 설정하였기에 최대 대기시간 제약조건이 고정된 최대 추가 차내 시간보다 더 작은 경우 대기시간을 더 우선시하는 배차를 수행하게 됨에 따라 이용자의 서비스 수락률이 감소하는 형태를 보였다. 전체적으로 볼 때, 최대 대기시간을 제약조건을 완할수록 차량 경로 통행시간만을 활용하기 보다는 이용자의 서비스 효용을 배차 알고리즘의 비용함수에 반영하는 것이 운영자와 이용자 관점 모두에서 긍정적인 영향이 있음을 확인하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-06/N0210420606/images/kst_2024_426_706_F4.jpg

Figure 4.

Operator perspective index (upper), user perspective index (middle), demand-supply index (lower) by maxinum waiting time

2. 최대 추가 차내 시간 변수 실험 결과

Figure 5는 수요대응형 배차 알고리즘 상 최대 추가 차내 시간 제약조건을 변경하면서 시뮬레이션을 수행한 결과를 나타낸다. 첫 번째 그래프는 운영자 서비스 지표에 대한 그래프로 최대 추가 차내 시간을 제약조건을 완화하는 경우 차량 통행거리 당 서비스 인원 수가 감소하는 형태를 보인다. 또한, 최대 대기시간 제약조건 변수 시뮬레이션 결과와 유사하게 이용자 효용 기반 비용함수 적용하는 경우 상대적으로 더 높은 운영자 효율을 갖는 것으로 나타났다.

두 번째 그래프는 이용자 서비스 지표에 대한 그래프로 최대 추가 차내 시간이 길어질수록 총 통행시간 대비 지연시간의 비중이 증가하는 경향을 보였다. 그 중에서도 차량 경로 통행시간 기반 비용함수를 활용하는 경우 추가 차내 시간 제약조건을 완화할수록 이용자 효용을 고려한 다른 두 비용함수 결과물에 비하여 지연시간 비중이 가파르게 상승하는 형태를 보였다. 앞선 최대 대기시간 제약조건 변수 결과물과 연계하여 살펴보면 최대 추가 차내 시간 제약조건이 통행지연을 방지하는데 효과적임을 알 수 있다.

세 번째 그래프에 따르면 차량 경로 통행시간 기반 비용함수 배차를 수행하는 경우 최대 추가 차내 시간 제약조건을 완화할수록 서비스 수락이 근소폭 감소하는 경향을 보였습니다. 반면, 이용자 효용을 반영하여 배차를 수행하는 경우 추가 차내 시간 제약조건과 관계없이 약 30%의 수락률을 안정적으로 유지하는 것으로 나타났다. 이 결과는 이용자 효용을 반영한 배차 전략이 차량 경로 통행시간 기반 배차에서 운영자가 경험이나 도메인 지식을 활용해 설정해야 하는 추가 차내 시간 제약 조건을 대체할 수 있음을 시사한다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-06/N0210420606/images/kst_2024_426_706_F5.jpg

Figure 5.

Operator perspective index (upper), user perspective index (middle), demand-supply index (lower) by maxinum additional in-vehicle time

3. 이용자 효용 가중치에 따른 실험 결과

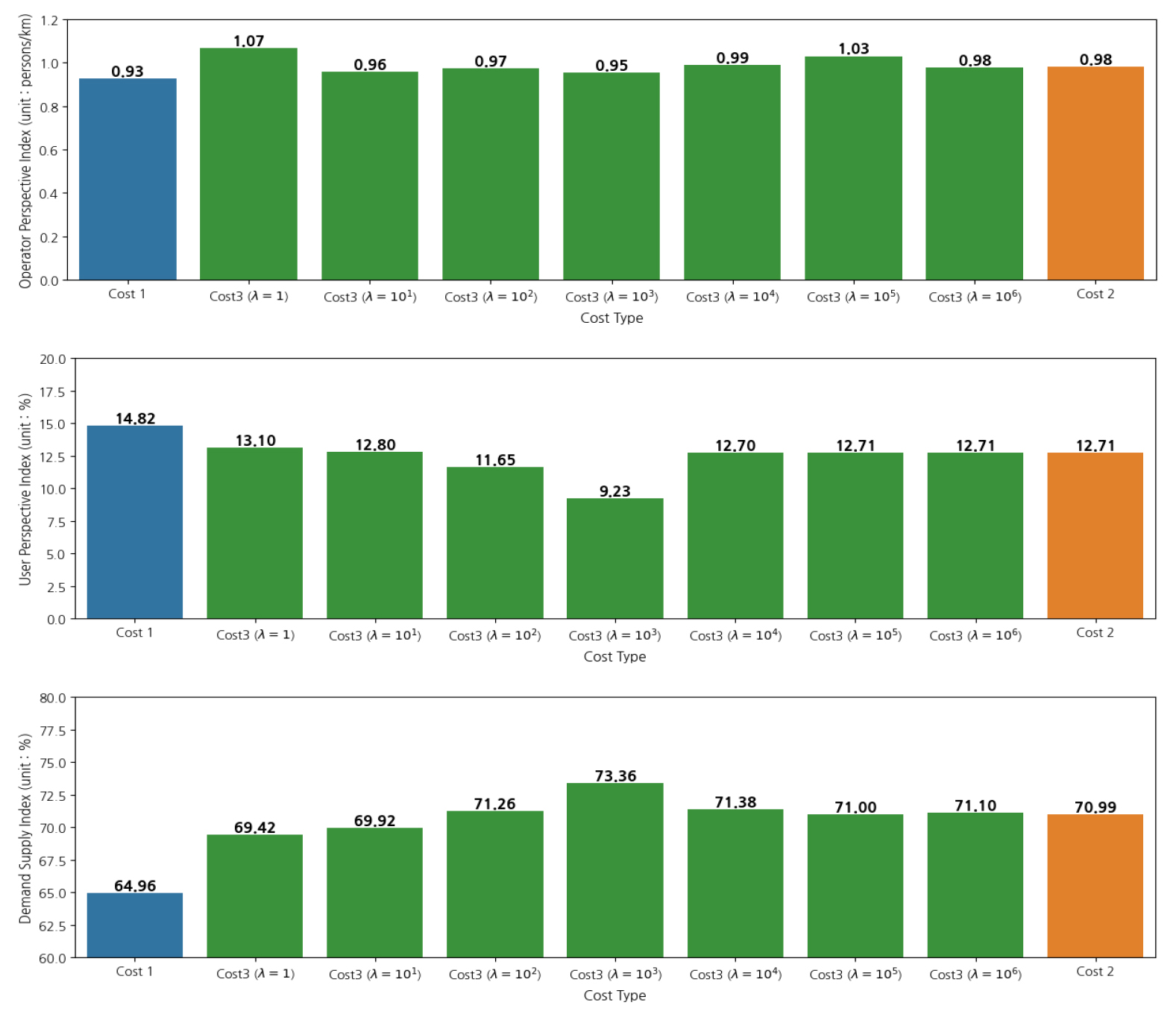
제 3장의 2절에서 언급하였듯 본 연구에서 활용한 차량 경로 통행시간과 이용자 효용 함수 합의 역수는 스케일의 차이가 존재한다. 최대 대기시간과 최대 추가 차내 시간 제약조건을 10분으로 고정하고, 이용자 효용 함수 가중치를 1로 설정하여 시뮬레이션을 수행한 결과, 차량 경로 통행시간에 비해 이용자 효용 함수 합의 역수는 평균적으로 약 -2575배의 스케일 차이를 보였다. 특히, 동일한 호출에 대하여 제약조건을 만족하는 경로 집합의 통행시간에 대한 표준편차의 평균은 0.112으로 나타났으며, 이용자 효용 최소값은 -0.627, 최대값은 –0.0027로 확인되었다. 이를 통해 두 비용함수를 결합한 모형에서 가중치 $λ$ 를 1로 고정할 경우 차량 매칭 시 차량 경로 통행시간 부문이 이용자 효용보다 우세하게 작용한다는 점이 드러났다. 이에 본 연구에서는 두 비용함수를 결합하는 과정에서 가중치를 1부터 10⁶까지 변화시키며 총 7번의 추가 실험을 수행했다.

Figure 6는 가중치에 따른 추가 실험 결과로 모든 가중치에 대하여 차량 경로 통행거리 대비 서비스 인원 수의 차이는 0.5 미만의 근소한 차이를 보였으나, 서비스에 대한 신뢰성을 나타내는 이용자 관점 지표는 두 지표가 경쟁할수록 우수한 형태를 보였다. 특히, 이용자 효용 함수 합의 역수에 1000만큼 가중치 $λ$ 를 부여하여 차량 경로 통행시간과 결합한 비용함수에서 더 높은 실 수요 비율을 보였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-06/N0210420606/images/kst_2024_426_706_F6.jpg

Figure 6.

Operator perspective index (upper), user perspective index (middle), demand-supply index (lower) by cost type

결론

본 연구는 수단 또는 서비스 선택 연구에서 논의된 통행시간 요소별로 이용자가 체감하는 효용이 서로 다르다는 점을 실시간 수요대응형 동적 경로 생성 과정에 적용했다는 점에서 의의가 있다. 또한, 경로 매칭 상황에서 호출 취소가 발생할 수 있다는 점을 고려하여 시뮬레이션 결과를 토대로 이용자의 배차 수락률을 확인하였다. 그 결과 운영자 관점과 이용자 관점 모두에서 차량 경로 통행시간을 기반으로 비용함수를 구성하여 배차를 수행하는 경우보다 통행정보에 따른 이용자 효용을 적용하여 비용함수를 구성하는 것이 모든 하이퍼 파라미터 시뮬레이션 상황에서 효과적임을 확인하였다. 더불어, 차량 배차 성공 횟수 대비 이용자 실 수락 횟수에 대한 비율을 비교한 결과 차량 경로 통행시간과 이용자 효용을 결합한 비용함수가 상대적으로 높은 퍼포먼스를 보인다는 점을 확인하였다. 실제 서비스 환경에서는 이용자의 승차가 완료되기 전 호출 취소가 발생할 가능성이 있다는 점에서, 이용자 효용을 배차 알고리즘에 반영하는 것이 실 수요를 확보하고 유연하며 이용자 친화적인 서비스를 제공하는 데 기여할 수 있다. 다만, 잠재선호 기반 효용을 배차 프레임워크에 적용하려면 서비스 현장에서 설문조사나 서비스 선호 데이터를 수집해야 하므로, 초기 서비스 구축 시 비용이 발생한다. 그러나 수요대응형 서비스는 이용자의 능동적인 배차 요청에 의존하는 특성을 지니고 있어, 지속가능한 운영을 위하여 이용자 선호을 적극반영하여 사용 경험을 향상시키고 재이용 의사를 확보하는 것이 필요하다. 따라서, 수요대응형 서비스를 고도화하는 과정에서 빠르고 효율적인 배차도 중요하지만, 본 연구와 같이 이용자의 선호를 파악하여 실 수요를 확보하는 전략을 검토하는 것이 필요하다. 또한, 제시한 배차 전략은 잠재선호 조사뿐만 아니라, 서비스를 운영하면서 누적된 서비스 호출자의 실 이용 데이터를 활용하여 효용모형을 추정할 수도 있다는 점에서 확장 가능성이 있다.

한편, 수요대응형 서비스는 호출 상황과 서비스 권역에 영향을 받는다는 점에서 다양한 수요 패턴 및 네트워크 권역에서 비교 검증이 필요하다. 본 연구에서 활용한 시뮬레이션 대상지는 중앙 노드를 중심으로 반경 1.9km 내 서비스 권역만을 대상으로 분석을 수행하였기에 서비스 권역을 넓어지는 경우 다른 양상을 보일 수 있다. 또한, Door-to-door 서비스에 가깝게 승하차가 가능한 노드 및 링크가 상세화 되는 경우 차량의 경로 변화가 더 크게 발생할 수 있다는 점에서 다양한 시나리오를 구성하여 검증을 수행할 필요가 있다. 더불어, 시뮬레이션 결과에서 제시하였 듯 삽입 휴리스틱을 활용한 본 배차 프레임워크는 수요가 많아질수록, 서비스 권역이 넓어질수록 탐색시간이 호출 수요의 $n$ 에 대하여 $(2 n!) / 2^{n}$ 만큼 증가하기 때문에 실제 운영시 본 연구를 적용하기 위해서는 병렬처리가 가능한 동적 최적화가 필요하다. 나아가, 교통 서비스에 대한 선호는 이용자별 경험과 속성에 따라 다르다는 점에서 향후 연구에서는 이용자의 신체적, 물리적 교통 환경에 따른 개인 선호를 반영하는 연구가 필요하다.

Funding

This work is supported by the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant 24AMDP-C161756-04).

알림

본 논문은 대한교통학회 제91회 학술발표회(2024.09.27)에서 발표된 내용을 수정·보완하여 작성된 것입니다.

References

Attanasio A., Cordeau J.-F., Ghiani G., Laporte G. (2004), Parallel Tabu Search Heuristics for The Dynamic Multi- vehicle Dial-a-ride Problem, Parallel Comput, 30(3), 377-387.

10.1016/j.parco.2003.12.001

Cappart Q., Thomas C., Schaus P., Rousseau L.-M. (2018), A Constraint Programming Approach for Solving Patient Transportation Problems, The International Conference 24th Principles and practice of constraint programming, 490-506.

10.1007/978-3-319-98334-9_32

Carotenuto P., Martis F. (2017), A Double Dynamic Fast Algorithm to Solve Multi-vehicle Dial-a-ride Problem, Transp. Res. Procedia, 27, 632-639.

10.1016/j.trpro.2017.12.131

Çetin T. (2017), The Rise of Ride Sharing in Urban Transport: Threat or Opportunity? In Urban transport systems, IntechOpen, London, UK.

10.5772/66918

Chassaing M., Duhamel C., Lacomme P. (2016), An ELS-based Approach with Dynamic Probabilities Management in Local Search for The Dial-a-ride Problem, Eng. Appl. Artif. Intell., 48, 119-133.

10.1016/j.engappai.2015.10.002

Cook R. D., Nachtsheim C. J. (1980), A Comparison of Algorithms for Constructing Exact D-Optimal Designs, Technometrics, 22(3), 315-324.

10.1080/00401706.1980.10486162

Cordeau J.-F., Laporte G. (2003), A Tabu Search Heuristic for The Static Multi-vehicle Dial-a-ride Problem, Transp. Res. Part B Methodol., 37, 579-594.

10.1016/S0191-2615(02)00045-0

Cordeau J. F., Laporte G. (2007), The Dial-a-Ride Problem: Models and Algorithms, Ann. Oper. Res., 153(1), 29-46.

10.1007/s10479-007-0170-8

Coslovich L., Pesenti R., Ukovich W. (2006), A Two-phase Insertion Technique of Unexpected Customers for A Dynamic Dial-a-ride Problem, Eur. J. Oper. Res., 175, 1605-1615.

10.1016/j.ejor.2005.02.038

Desrosiers J., Dumas Y., Soumis F. (1986), A Dynamic Programming Solution of The Large-scale Single-vehicle Dial-a-ride Problem with Time Windows, Am. J. Math. Manag. Sci., 6(3-4), 301-325.

10.1080/01966324.1986.10737198

Häll C. H., Andersson H., Lundgren J. T., Värbrand P. (2009), The Integrated Dial-a-Ride Problem, Public Transport, 1(1), 39-54.

10.1007/s12469-008-0006-1

Ho S. C., Szeto W. Y., Kuo Y.-H., Leung J. M. Y., Petering M., Tou T. W. H. (2018), A Survey of Dial-a-ride Problems: Literature Review and Recent Developments, Transp. Res. Part B Methodol., 111, 395-421.

10.1016/j.trb.2018.02.001

Lee J., Kim J., Chung J.-H. (2022), Effect of Personal Attitudes and Satisfaction with Public Transportation on Stated Preference of Automated Mobility-on-demand, J. Korean Soc. Transp., 40(1), Korean Society of Transportation, 81-98.

10.7470/jkst.2022.40.1.081

Lehuédé F., Masson R., Parragh S. N., Péton O., Tricoire F. (2014), A Multi-criteria Large Neighbourhood Search for The Transportation of Disabled People, J. Oper. Res. Soc., 65, 983-1000.

10.1057/jors.2013.17

Luo Y., Schonfeld P. (2011), Online Rejected-reinsertion Heuristics for Dynamic Multivehicle Dial-a-ride Problem, Transp. Res. Rec., 2218(1), 59-67.

10.3141/2218-07

Nasri S., Bouziri H., Aggoune-Mtalaa W. (2021), Customer-oriented Dial-a-ride Problems: A Survey on Relevant Variants, Solution Approaches and Applications, The Proceedings of NICE2020 International Conference, Emerging Trends in ICT for Sustainable Development, 111-119.

10.1007/978-3-030-53440-0_13

Psaraftis H. N. (1980), A Dynamic Programming Solution to The Single Vehicle Many-to-many Immediate Request Dial-a-ride problem, Transp. Sci., 14(2), 130-154.

10.1287/trsc.14.2.130

Ropke S., Cordeau J.-F., Laporte G. (2007), Models and Branch-and-cut Algorithms for Pickup and Delivery Problems with Time Windows, Networks, 49(4), 258-272.

10.1002/net.20177

Solomon M. (1987), Algorithms for the Vehicle Routing and Scheduling Problems with Time Windows Constraints, Oper. Res., 35(2), 254-265.

10.1287/opre.35.2.254

Stein D. M. (1978), Scheduling Dial-a-Ride Transportation Systems, Transp. Sci., 12(3), 232-249.

10.1287/trsc.12.3.232

Vallee S., Oulamara A., Cherif-Khettaf W. R. (2020), New Online Reinsertion Approaches for A Dynamic Dial-a-ride Problem, J. Comput. Sci., 47, 101199.

10.1016/j.jocs.2020.101199

Wong K. I., Han A. F., Yuen C. W. (2014), On Dynamic Demand Responsive Transport Services with Degree of Dynamism, Transportmetrica A: Transport Science, 10(1), 55-73.

10.1080/18128602.2012.694491

Youm J., Lee J., Chung J.-H., Kim J. (2023), A Study of Automated Mobility-on-demand Service Acceptance Rate Based on Stated Preference Survey, J. Korean Soc. Transp., 41(4), Korean Society of Transportation, 538-551.

10.7470/jkst.2023.41.5.538

Journal of Korean Society of Transportation ISSN:1229-1366(Print) 2234-4217(Online) 대한교통학회지