서론
선행연구
분석 자료 구축
1. 대안 경로 집합 구축
2. 모형 설명변수 구축
Path-Size 로짓 모형 구축
1. Path-size 로짓 모형
2. 모형 정산 및 최적 파라미터 ν 도출
경로 선택 모형 구축 결과
모형 정확성 검증
결론
서론
통행자의 통행 선택 행태에는 빈도 선택, 목적지 선택, 수단 선택, 경로 선택, 출발시각 선택의 5가지가 포함되어 있다. 여기서 경로 선택은 통행자가 인지하고 있는 대안 경로(Alternative path) 여러 개를 고려하고 가장 최적의 경로를 선택하는 행태이다. 이러한 통행자의 경로 선택 행태를 수학적 모형으로 표현하는 방법에는 통행자가 대안 경로를 선택할 확률을 고려한 확률적 경로 선택 방법(Stochastic route choice)과 고려하지 않은 결정적 경로 선택(Deterministic route choice)방법이 있다(Huang et al., 2008). 여러 연구를 통해서 결정적 경로 선택 방법보다 확률적 경로 선택 방법으로 통행자의 선택 행태를 설명하는 것이 현실적으로 더 적합하다고 알려져 있다(Tatineni et al., 1997; Prato, 2009). 또한 경로 선택에는 통행시간, 거리, 비용, 지체 정도, 도로 위계, 정시성, 습관 등의 다양한 변수들이 고려되며 통행자마다 중요하게 생각하는 요소가 다르기 때문에 같은 기종점 간 대안 경로가 다양하다(Ortúzar and Willumsen, 2011).
하지만 현재에 이르기까지 실무적 네트워크 분석에 의한 교통정책 결정에 있어 확률적 모형보다 결정적 모형인 Beckmann et al.(1956)의 수식에 의한 사용자 균형 모형이 보편적으로 사용되고 있다. 그 이유는 첫 번째로 결정적 모형은 통행시간과 요금만 설명변수로 사용하여 계산의 용이성이 있으며 수학적 유일해(Unique solution)를 가져 분석의 편의성이 있다. 두 번째로 확률적 경로 선택 모형의 기반이 되는 다항 로짓 모형(Multinomial logit model)은 비관련 대안(Independent of Irrelevant Alternatives, 이하 IIA)특성을 가지며, 이는 대안 경로 겹침에 따른 선택 행태를 반영할 수 없어 노선배정(Traffic Assignment) 분석에서 비현실적 분석 결과를 도출할 수 있다. 마지막으로 확률적 모형을 분석하기 위한 전제 조건으로 대안 경로 집합 구축(Path enumeration) 과정이 필요하다. 이를 위해서 통행 궤적 자료가 필요하지만 실측 관측 자료를 취득할 수 있는 방법은 표본 조사 밖에 없어 확률적 경로 선택 방법의 실무적 적용에 한계점이 있었다. 이러한 이유로 기존 연구들에서 경로 선택 모형을 구축하기 위한 자료로 설문조사 자료나 가상 시뮬레이션 환경에서의 적은 양으로 구축된 궤적자료를 사용하였다(Park et al., 2007; Lee et al., 1999; Lee and Baek, 2005).
그러므로 본 연구에서는 확률적 모형이 실무적 분석에 적용될 수 있도록 Ben-Akiva and Ramming(1998)이 제안한 경로 겹침을 고려한 선택 행태를 반영할 수 있는 Path-size 로짓 모형을 사용하여 경로 선택 모형을 정산하였다. 또한 내비게이션 자료는 통행자들이 통행한 출발-도착 두 지점 간의 실측 경로 집합을 파악할 수가 있다. 그러므로 내비게이션 자료를 이용하여 대안 경로 집합을 구축하고 확률적 경로 선택 모형을 정산하였다. 비록 내비게이션 자료 역시 모든 통행자들의 자료로 구성되어 있지 않은 표본자료에 해당하지만 자료의 수가 기존연구에서의 표본 조사 자료에 비해 비교할 수도 없는 규모로 많다는 장점이 있다. 또한 궤적 자료는 GPS(Global Positioning System)를 이용하여 자동 저장되고 있어 단순히 통행자의 기억에 의존하는 자료보다 정확성이 높고 자료조사의 비용이 적다는 장점을 갖고 있다. 이와 같이 내비게이션 자료는 과거 경로 선택 행태 연구의 어려움을 극복할 수 있는 자료라는 장점을 가지고 있다.
본 연구에서는 내비게이션 자료를 이용하여 경로 선택 모형을 구축하므로 공로 경로 선택에 대해서만 고려하였다. 사용한 자료는 SK T-map 어플리케이션으로 수집되었다. 자료 수집 기간은 2016년 7월 18-22일이며 승용차, 화물차, 버스 등 다양한 수단 이용자들의 개별 경로 자료이다. 수단 선택 행태는 통행 요금과 관련이 있으며 통행 요금은 차종별로 상이하다. 하지만 연구에서 사용한 자료 구조에서는 차종에 대한 정보는 알 수 없었으며, 이러한 한계로 모형 정산에서 차종에 맞는 통행 요금 산정을 할 수 없었다. 그러므로 모든 통행의 요금은 가장 일반적인 승용차 수단을 기준으로 산정하였다.
본 연구는 통행자의 중장거리 통행에 대한 경로 선택 행태를 분석하였다. 단거리 통행과 중장거리 통행의 경로 선택 행태는 차이가 있을 수 있다. 단거리 통행은 통행자가 지리를 잘 인지하고 있으며 반복적으로 발생하는 통행인 출퇴근 목적 통행을 포함하고 있다. 이러한 통행은 시간대 별 교통체증 상태에 대한 인지도가 높으며 위계가 낮은 국지도로가 포함된 경로를 많이 이용하기도 한다. 반면에 중장거리 통행은 대부분 비정기적으로 발생하는 목적의 통행이다. 그러므로 통행자는 도로 위계가 높은 도로를 포함하는 경로를 더 많이 이용하는 경향이 있다. 통행자의 통행거리에 따른 경로 선택 행태가 상이할 수 있기 때문에 모든 통행거리에 대한 경로 선택 행태를 분석하지 않았으며 중장거리 통행에 대한 분석만 수행하였다. 그러므로 SK T-map을 이용하는 통행자들이 내비게이션을 대부분 활성화 한다고 할 수 있는 100km 이상 장거리 통행에 대해서만 분석을 진행하였다. 공간적 범위는 전국이며 시간적 범위는 자료 수집기간이다. 본 연구의 또 다른 목적은 한국교통연구원에서 정기적으로 조사되고 있는 가구통행실태조사에서 취득하기 어려운 장거리 통행조사를 보완하기 위해 사용되는 대중교통의 실적자료와 고속도로 TCS 자료 외에 내비게이션 자료를 활용한 장거리 통행 조사 방법을 제안하는 것이다. 따라서 KTDB 자료 중 시군구단위 존체계인 전국 교통망의 분석대상이 되는 장거리 통행 경로 선택 행태를 분석하였다.
선행연구
통행자의 경로 선택 행태 연구는 교통 인프라 구축이나 경로안내 시스템 구축 등 다양한 교통운영 관련 교통정책 수립 시 필요한 기초 연구이다. 특히 도로 건설, 대중교통 시스템 개편 등으로 인하여 통행자의 경로 선택 행태에 따라 해당 노선이나 도로의 장래 수요 추정 통행량이 변동될 수 있으므로, 통행자의 경로 선택 행태에 대한 고려는 중요하다. 경로 선택 행태 연구는 대중교통 경로 선택 연구(Eluru et al., 2012; Jánošíková et al., 2014; Kim et al., 2020), 자전거 경로 선택 연구(Sobhani et al., 2019), 공로 경로 선택 연구(Frejinger et al., 2006; Frejinger and Bierlaire, 2007; Lee and NamGoong, 2002; Hess et al., 2015; Kim, 2014) 등 다양하다.
연구에서 고려하는 공로 경로 선택에 관한 선행연구에서 사용한 자료는 대부분 표본자료, 소규모 GPS 수집자료, 설문조사 자료이다(Ciscal-Terry et al., 2016; Frejinger and Bierlaire, 2007; Lee and Baek, 2005; Lee and NamGoong, 2002; Amirgholy et al., 2017). Kim et al.(2020)은 이러한 표본자료나 설문조사 자료를 사용한다면 모형의 정확성이 떨어진다고 언급하였다. 근래 과학기술의 발전으로 빅 데이터 수집 및 저장이 가능해지면서 내비게이션 자료를 이용한 연구들이 증가하고 있다(Lee and Um, 2009; Park et al., 2015; Park and Lee, 2017; Song, 2019; Wang et al., 2017). 또한 내비게이션 자료와 같이 규모가 크고 통행자의 위치를 수집하는 데이터인 휴대폰 자료나 고속도로 궤적자료를 이용한 경로 선택 모형 연구도 이루어지고 있다. Kim(2014)은 DSRC(Dedicated Short Range Communication)자료를 이용하여 경로 선택 모형을 제시하였다. 하지만 DSRC 자료에서는 통행자의 정확한 출 ‧ 도착 위치를 알 수 없어 대안 경로의 기종점은 고속도로 IC이며 고속도로만을 대안 경로 집합으로 고려한 한계점이 존재하였다. Bwambale et al.(2019)는 CDR(Call Detail Record) 자료를 이용하여 장거리 도로 통행의 경로 선택모형을 정산하였다. 하지만 CDR자료에서 통행자의 위치는 통신 기지국 단위로 수집되어 정확히 어떠한 도로를 이용하였는지 알 수 없다. 그러므로 Bwambale et al.(2019)은 통행자의 통행 궤적을 링크 및 도로가 아닌 기지국이 포함된 행정구역들로 표현하고 행정구역들을 잇는 포장된 도로를 통행 경로로 설정하였다. 또한 CDR 자료에서는 관측된 통행시간을 알 수 없어 실제 통행자의 통행시간을 모형 구축에 사용할 수 없었으며 OD 한 쌍에 대한 경로 선택 모형을 구축하였다. 본 연구에서 사용한 자료는 SK T-map 어플리케이션으로 수집된 자료로 관측 시점 자료에 근거하면 대략 하루 평균 450만 명의 운전자가 이용하고 있었다. 이러한 규모가 큰 데이터를 이용함으로써 본 연구는 적은 표본자료를 이용한 경로 선택 모형이 가지는 단점을 극복하였다. 또한 내비게이션 자료에서 관측된 통행시간과 정확히 제시된 도로 단위의 통행 궤적 자료를 이용하여 모형을 구축하고 고속도로와 고속도로 외 도로들로 대안 경로 집합을 구성하여 대규모 표본자료를 사용한 기존연구들의 한계점을 극복하였다.
경로 선택의 경우는 대안 경로 간의 중첩문제(Overlapping problem)가 보편적이기 때문에 보편적으로 사용하는 다항 로짓 모형을 적용하기에는 한계가 있다. 이러한 한계점을 완화하기 위해 여러 학자들이 다항 로짓 모형을 바탕으로 C-로짓 모형, Path-size 로짓 모형, Link-nested 로짓 모형 등의 개발에 노력하여 왔다. C-로짓 모형은 Cascetta et al.(1996)이 제시한 방법으로 로짓 모형에서 계산의 단순성을 유지하면서 경로 겹침에 대한 문제를 해결하는 방법이다. 이 모형은 경로 겹침 문제를 해결하기 위해 다른 경로와 겹치는 정도를 기반으로 하는 공통성 인자(Commonality factor)를 모형에 추가하였다. 하지만 위 모형은 공통성 인자의 해석이 직관적이지 않으며 다양한 공통성 인자 공식 중에 어떠한 것을 사용해야 할지에 대한 이론적인 뒷받침이 부족한 단점이 존재한다(Tan et al., 2015).
Path-size 로짓 모형(이하 PS-로짓 모형)은 전체 경로에서 다른 경로와의 중첩 부분의 크기를 고려한 모형으로 Ben-Akiva and Ramming(1998)에 의해 소개되었다. PS-로짓 모형은 전체 경로에서 다른 경로와의 중첩 부분의 크기를 나타내는 수치인 PS변수를 경로 효용함수에 추가한 형태이다. Ben-Akiva and Bierlaire(1999)은 해당 대안의 링크와 중첩되는 다른 대안의 최단 경로의 거리()를 고려한 PS-로짓 모형을 제시하였다. Ramming(2002)은 Ben-Akiva and Bierlaire(1999)의 PS계산 공식에 스케일 파라미터()를 적용하여 일반화된 PS-로짓 모형(Generalized PS Logit) 모형을 제시하였다. Tan et al.(2015)은 대중교통 네트워크에서 경로 선택을 위한 배차간격 기반 PS-로짓 모형을 제시하였다. 싱가포르의 교통카드 자료에서 관측된 경로들을 대상으로 다항 로짓 모형, PS-로짓 모형, 배차간격 기반 PS-로짓 모형을 이용하여 예측한 결과 배차간격 기반 PS-로짓 모형이 더 좋은 예측 정확도를 보였다. Link-Nested 로짓 모형은 Vovsha and Bekhor(1998)이 제안한 모형으로 Cross-Nested 로짓 모형을 확률선택 문제에 적용한 모형이다. 이 모형은 실제 네트워크에 사용할 수 있는 가장 적합한 방법이지만 계산이 복잡하여 효율성이 떨어지는 단점이 있다.
기존 연구의 다양한 확률적 경로 선택 모형 중 내비게이션 자료에 적용이 용이한 모형이면서 경로 간 중첩 부분의 크기를 고려한 PS-로짓 모형이 본 연구에 가장 적합하다고 판단하였다. PS-로짓 모형을 사용하여 공로 경로 선택 모형을 구축한 연구가 다수 있었으나(Frejinger et al., 2006; Frejinger and Bierlaire, 2007) Bwambale et al.(2019)의 연구를 제외하고 소규모의 표본자료를 사용한 한계점이 있다. Bwambale et al.(2019)은 대규모 CDR 자료를 이용하여 PS-로짓 모형을 구축하였다. 하지만 앞에서 언급한 것처럼 모형 구축 과정에서 CDR 자료의 한계점으로 인하여 통행자의 정확한 통행 궤적과 통행시간을 알 수 없었다. 따라서 본 연구는 대규모로 관측된 내비게이션 자료를 이용하여 자료의 규모에 의해 발생할 수 있는 표본자료에 의한 오차(Sampling error)보다 최소화하여 과거 연구의 한계점을 완화하였으며 통행자의 정확한 궤적과 통행시간을 이용하여 모형을 정산하였다. 또한 경로 겹침 문제를 고려할 수 있는 PS-로짓 모형을 구축하여 통행자의 경로 선택 행태를 연구하였다.
분석 자료 구축
본 연구에서 내비게이션 자료 구축 과정은 데이터 전처리, 대안 경로 구축, 설명변수 구축 순서로 진행되었다. 데이터 전처리 과정에서는 첫 번째로 내비게이션 자료의 형태를 수정하였다. 내비게이션 자료에서 통행자 별 통행 궤적은 연속된 링크(link)들로 표현되어 있다. 이러한 통행 출발지와 도착지 사이의 연속된 링크들을 기종점을 가지는 한 개의 경로 형태로 수정하였다. 두 번째는 자료 내 오류 데이터를 제거하거나 수정하였다. 통행자의 통행시간이 1일 이상이거나 경로 내 링크의 진입시간과 진출시간이 현실적이지 않은 경우는 분석에서 제외하였다. 또한 내비게이션 신호의 오류로 인하여 연속적인 주행 궤적 자료에서 결측 값을 가지는 링크의 도로 등급 및 속도는 해당 링크와 전 ‧ 후로 연결되는 링크들의 속성과 같다고 가정하였다. 그리고 분기점 없이 교차하는 두 개의 고속도로 링크에서 통행자의 위치를 주행 링크가 아닌 교차된 링크로 인식하여 발생하는 오류를 수정하였다. 데이터 전처리 과정 이후에 경로 선택 모형 정산을 위해 대안 경로 집합을 구축하고 경로 선택 행태와 관련이 있는 설명변수를 경로 별로 구축하였다.
1. 대안 경로 집합 구축
본 연구는 경로 선택 모형 정산을 위해 기종점 간 대안 경로 집합을 구축하였다. 내비게이션 자료는 출발지점과 도착지점이 도로(link)로 표시되어 있어 일정한 공간단위로 집합화하는 과정이 필요하다. 출발 존과 도착 존의 공간적 집합 규모에 따라 출발지점-도착지점(origin-destination, OD) 조합의 수와 각 OD의 자료 수가 다르다. 연구의 공간적 범위는 우리나라 전국을 대상으로 하므로 교통존이 너무 세분화될 경우 각 OD 쌍 조합에 대한 자료 수가 부족하게 되어 경로 선택 행태분석이 어렵게 된다. 출발 및 도착 지점에 대한 공간적 집합 단위인 교통존 규모를 읍면동 단위로 설정할 경우 표본 수가 부족하였다. 그러므로 본 연구에는 중장거리 통행의 경로 선택모형은 시군구 행정단위의 교통존 체계가 적합한 것으로 판단하여 KTDB 전국권 자료와 동일한 시군구 단위의 교통존 체계로 대안 경로 집합을 구축하였다. 또한 각 기종점 쌍 간 내비게이션 관측 통행수가 10통행이 넘는 기종점 자료를 사용하여 확률적 경로 선택모형의 정산 분석을 수행하였다.
도로망이 복잡하게 얽혀 있을수록 혹은 중장거리 통행과 같이 통행거리가 멀어질수록 내비게이션 자료에서 같은 기종점 간 실제 이용된 통행경로는 다양하고 그 숫자는 점차 커지는 경향이 있다. 이러한 수많은 대안 경로들을 모두 다른 경로로 설정한다면 통계적으로 유의한 대안으로 구성하기도 어려울 뿐 아니라 각각 대안 경로 당 자료 수도 매우 적게 되어 유의미한 모형 결과를 도출할 수가 없게 된다. 그러므로 본 연구는 통행 경로를 집합화 하는 과정을 수행하였다. 내비게이션 자료의 기종점을 시군구 단위로 집합화 하였으므로, 시군구 내부에서 고속도로를 이용하기 위한 접근경로가 실제 내비게이션에서 상이하더라도 중장거리 통행이 주로 이용하게 되는 상위 위계도로 등급에 해당되는 고속도로나 도시고속도로의 이용 궤적과 거리가 유사하다면 같은 경로로 가정하였다. 이는 교통 네트워크 분석에서 통행들의 출발 및 도착지점을 집합화하여 1개의 대표 노드인 센트로이드로 표현한 개념과 같은 의미이다. 그러므로 이론적으로 문제가 없을 것이라 판단하였으며, 같은 기종점 간 고속도로나 도시고속도로 이용거리가 같은 경로는 동일한 경로로 집합화 하였다.
고속도로는 접근성이 낮으며 도로가 촘촘하게 구성되어 있지 않으므로 고속도로를 이용하는 대안 경로는 명확하게 존재하며 표본수가 적당하였다. 그러나 국도, 시군도, 지방도와 같이 위계가 낮은 도로는 접근성이 좋은 만큼 대안 경로의 수는 분석에서 고려할 수 있는 규모를 훨씬 넘게 존재할 수 있다. 각 통행 경로를 모두 대안 경로로 설정한다면 경로 당 표본수가 적어 경로 선택 행태를 설명하기 어려우며, 자료가 충분이 있더라도 모형의 복잡도가 증가하여 명쾌한 통행자 경로 선택행태를 규명하고 해석하기 어렵다. 이러한 이유로 고속도로를 이용하지 않는 대안 경로들을 집합화하여 한 개의 대안 경로로 설정하였으며, 집합화된 경로의 통행시간과 비용은 평균값을 산출하여 모형에 적용하였다.
그러므로 본 연구에서 기종점 간 대안 경로는 고속도로를 이용하는 경로들을 우선적으로 구축하였다. 그리고 고속도로를 이용하지 않은 지방도 및 국도로만 구성된 경로를 이용한 자료 수가 통계적으로 유의한 만큼 존재할 경우는 경로들을 집합화 하고 대안 경로 집합에 추가하였다. 최종적으로 모형정산에 사용하는 자료 수는 총 120,830통행이며, 그 자료에 해당되는 기종점 수는 4,580개이다. Table 1은 통행거리 별 기종점 수, 기종점 당 평균 자료 수, 평균 통행 거리, 평균 통행 시간이다. 분석에 사용된 기종점들의 통행거리는 100-150km이 가장 많았으며 기종점의 평균 경로 수는 17개 이상이다.
Table 1.
Statistics of alternative path set
2. 모형 설명변수 구축
데이터 전처리 과정과 대안 경로 집합 구축을 한 후 모형의 설명변수인 통행 경로 별 속성자료를 구축하였다. 내비게이션 자료는 통행자 별 자료 수집 날짜, 통행 출발지, 도착지, 출발시간, 도착시간이 정보로 구성되어 있으며 자료의 링크 정보는 국가교통정보센터(National Transport Information Center)에서 제공하는 KS표준링크를 기준으로 구성되어 있다. 모형에서 설명변수로 사용될 수 있는 통행 경로의 속성인 경로 길이, 통행 경로 내 도로 위계 별 이용 비율, 차로 수 등은 내비게이션 자료에서 알 수 없다. 그러므로 내비게이션 자료의 기준 자료인 KS 표준링크 자료에서 통행 경로의 속성들을 추출하였다. 경로 선택에 영향을 미치는 주요 설명변수에 해당하는 경로의 통행 비용은 Korea Transport Database(2020)에서 제시한 한국도로공사 폐쇄식 요금소에서 승용차의 거리당 요금 체계를 이용하였으며 Table 2와 같다. 유료도로 이용요금은 기본 900원이며 주행단가/km는 도로의 차선 수에 따라 상이하다. 본 연구에서는 실무적으로 사용하는 유료도로 비용 산정 자료를 반영하여 통행료를 가능한 현실적으로 반영하도록 노력하였다.
Path-Size 로짓 모형 구축
1. Path-size 로짓 모형
대중교통 수단은 노선이 고정되어 있어 통행자의 경로 선택 행태에서 경로 전환이 자유롭지 않다. 도로 네트워크에서는 교차로 지점마다 경로 전환이 자유로워 통행자가 공로 경로 선택을 할 때 매우 많은 양의 다양한 경로 대안들이 가능하게 되며 여러 대안 경로들에서 중첩되는 구간이 많게 된다. 따라서 각 대안 간의 독립성을 기본 가정으로 개발된 로짓 모형을 이용하여 경로 선택 모형을 정산한다면 대안경로 간의 중첩구간문제(overlapping problem)가 발생하여 비현실적 경로 선택 행태를 야기하게 된다. 따라서 본 연구에서는 중첩문제를 해결하기 위해 Ramming(2002)이 제안한 일반화 PS 로짓 모형(Generalized path-size logit model)을 이용하여 경로 선택 행태모형을 정산하였다. 일반화 PS 로짓 모형은 기존 로짓 모형의 IIA 속성을 극복하기 위해 개발된 모형 중에서 경로 선택 행태모형 적용에 계산의 용이성을 가지며 효율성이 높고 정산 과정도 어렵지 않아 연구에 적용하였다.
일반화 PS 로짓 모형은 기존 로짓 모형의 IIA 속성을 극복하기 위해 개발된 모형 중에서 경로 선택 행태모형 적용에 계산의 용이성을 가지며 효율성이 높고 정산 과정도 어렵지 않아 연구에 적용하였다. 일반화된 PS 로짓 모형은 경로 간 중첩문제를 해결하기 위해 해당 대안의 전체 경로에서 다른 대안 경로와 겹치는 부분의 크기를 PS변수를 통해 고려한다. PS 로짓 모형의 경우는 C-로짓 모형과는 달리 통행길이에 따라 중첩 경로길이의 비율이 동일하더라도 다른 선택확률이 산출될 수 있으므로 좀 더 현실적 분석 결과를 제시할 수가 있는 특성을 가지고 있다. 예시로 전체 경로길이가 500km이면서 5km(1%)중첩일 때와 전체경로길이가 30km이면서 0.3km(1%)중첩일 때의 각 경로의 선택 확률이 달라지게 분석 결과가 도출될 수 있다. 대안 경로 간 겹치는 링크가 없을 경우 대안의 효용 변화가 없게 계산되는데 이때 PS 변수 크기는 1로 계산되어 일반적 로짓 모형과 동일한 결과가 도출된다. 일반화된 PS 로짓 모형은 Equation 1과 같으며 PS변수는 Equation 2와 같다.
여기서, : 통행자의 경로 선택 집합
: 통행자의 경로의 효용
여기서, : 대안 에 속한 모든 링크
: 링크 의 길이
, : 대안, 의 전체 길이(단, 대안 는 대안 와 중첩되는 모든 대안)
: 링크 가 대안에 속하면 1, 그렇지 않으면 0
Equation 2에서 PS 변수는 파라미터를 통해 중첩되는 링크의 영향을 일반화한 수치이다. 파라미터는 스케일 파라미터(scale parameter)로서 무한대에 가까워질수록 다항 로짓 모형 결과와 유사해지며 분석 자료의 특성과 규모를 고려하여 연구자가 자료기반의 정산 과정을 거쳐 추정되는 값이다(Ramming, 2002).
교통수단 선택행태를 이산선택모형(discrete choice model)으로 표현할 경우 모든 OD 쌍의 선택대안(교통수단)이 고정적이므로 대안 별 고정적인 고유 특성을 가질 수 있다. 하지만 경로 선택행태는 모든 OD 쌍의 대안 경로 집합이 상이하여 대안의 고유 특성을 가질 수 없다. 그러므로 대안 별 대안특성상수(alternative specific constant)를 설정할 수 없는 문제가 존재한다. OD 쌍 별 경로 선택 모형을 구축한다면 대안특성상수를 모형에 포함시킬 수 있지만 너무 복잡하고 방대하여 현실적 효용성이 부족하다는 문제점이 있다. 그러므로 본 연구에서도 대안특성상수를 포함하지 않는 효용함수로만 경로 선택 모형을 구축하였다.
현재 실무적으로 적용되고 있는 결정적 사용자 균형 상태를 찾는 경로 선택 분석은 시간단위로 전환된 통행요금과 통행시간만을 기준으로 분석이 이루어지고 있다. 오히려 본 연구에서 제시한 모형은 좀 더 다양한 대안 경로 별 속성을 포함하고 있어 실무적으로 적용되는 분석보다 경로 선택 행태를 통계적으로 더 잘 설명할 수 있을 것이라 고려된다. 또한 Sheffi(1985)에서 서술되어 있는 바와 같이 경로 선택에서는 통행시간과 다른 영향 요소들 간 상관관계가 높아 통행시간만을 기준으로 노선배정이 분석될 수 있다고 하였다. 그러므로 본 연구에서 제시한 모형의 효용함수에는 다른 영향 요소들을 집약적으로 묘사하게 되는 대안특성상수가 포함되지 않았지만 통행시간 및 기타 설명변수를 포함하였으므로 통행시간만을 기준으로 하는 기존 모형보다는 더 현실적으로 경로 선택 행태를 반영할 것으로 고려된다.
2. 모형 정산 및 최적 파라미터 ν 도출
도로 이용자들의 경로 선택 모형 정산에서 모형의 논리성, 변수의 통계적 유의성, 모형 전체 설명력이 뒷받침 되어야 할 것이다. 먼저, 모형의 논리성을 검토하기 위해서는 변수 계수의 부호를 검토하는데 해당 변수의 특성과 효용의 관계에서 논리성을 검증하게 된다. 모형의 설명변수에 대해서는 기본 단위 변화에 따른 효용 규모 변화에 영향을 미치는 정도가 통계적으로 유의미하게 설명하고 있는가를 검증하게 되는데 이때 적용하는 통계치로 t-value 및 p-value 가 있다. 통계적으로 유의할 경우 해당변수는 통행자의 통행 행태에 유의미하게 영향을 주고 있는 것으로 판단할 수 있으므로 경로 선택 모형의 설명 변수로 포함될 수 있으며, 모형 구성 단계에서 다른 설명변수와 함께 복합적 전체 설명력을 높이는 방향으로 설명변수들의 조합을 선택하게 된다. 모형의 전체 설명력은 회귀모형의 값이 갖는 의미와 유사한 으로 판단하며 그 값은 값과 동일하게 0-1사이의 값을 갖는다. 즉 값이 1에 가까울수록 현실 설명력이 높은 모형으로 해석할 수 있다. 일반적으로 가 0.2-0.3의 값 수준만 되어도 경험적으로 만족할 수 있는 수준의 모형으로 판단할 수 있다는 연구(McFadden, 1976)도 있지만 자료의 특성에 따라 값에 대한 통계학적 유의미 정도에 대한 해석에 차이가 있을 수가 있다. 또한 전체적인 모형 설명력이 높은 효용함수를 찾기 위해 설명변수를 추가 또는 변형한 모형과 기본 모형을 비교하기 위한 Log-likelihood Ratio 검정을 통해서 통계적으로 더 유의한 모형을 찾아가는 분석을 일반적으로 수행하게 된다. 본 연구에서는 먼저 파라미터를 1로 고정하여 모형의 함수적 특성과 계수 값의 논리성 검증, 개별 설명변수의 통계적 유의성 및 모형 전체적 설명력을 고려하면서 적합한 설명변수로 구성된 모형을 구축하였다. 그 후 적합한 설명변수들로 구성된 모형과 관측 자료를 기반으로 현실 현상을 가장 잘 설명할 수 있는 파라미터 값을 추정하였다.
PS 로짓 모형의 은 스케일 파라미터로서 구축하려는 경로 선택 모형에 적절한 값을 연구자가 결정하도록 Ramming(2002)에서 제시하였다. 하지만 그 의미가 매우 애매하기 때문에 본 연구에서는 내비게이션 자료에 기반하여 현실적인 경로 선택행태를 가장 잘 설명할 수 있는 값을 추정하였다. 앞서 를 1로 고정하여 정산된 모형의 변수들을 대상으로 의 변화에 따른 모형의 통계적 설명력()이 가장 높은 최적의 값을 도출하였다. 최적 값 도출 방법은 황금분할 탐색법(Golden-section search)으로 하였다. 황금분할 탐색법은 황금비율(Golden ratio)을 이용하여 단봉함수(Unimodal function)에서 최솟값 또는 최댓값을 탐색하는 방법이다.
경로 선택 모형 구축 결과
대안 경로 집합에서 단속류, 연속류 도로의 구성 정도에 따라 통행자의 경로 선택 행태가 다를 수 있다. 이러한 점을 고려하여 Model 1에 통행시간()과 통행거리() 변수를 모두 모형에 포함하여 분석을 시도하였다. 또한 경로 선택 행태와 관련이 있을 것으로 판단되는 통행비용()을 설명변수로 포함하여 Model 1(Equation 3)을 설정하였다(Table 3). Table 4의 모형 정산 결과에서 통행시간과 통행거리에 대한 계수 부호가 논리적으로 예상되는 결과와 상반되어 예측모형으로 선정하기 어려웠다. 이와 같은 연구 결과는 ‘통행자는 일반적으로 통행시간이나 통행거리가 짧은 경로를 선택하지만, 도로 위계가 높은 연속류 도로를 선호하는 경향이 있기 때문에(Chen and Li, 2015) 통행거리나 통행시간이 단속류 도로 보다 길더라도 선택하는 행태가 나타난다(Bwambale et al., 2019).’ 라고 설명된 것과 유사한 분석 결과이다.
Table 3.
Alternative configuration of route choice model (=1)
Table 4.
The calibration result of model 1-3
본 연구에서는 Model 1에서 사용된 설명변수인 통행시간, 통행거리, 통행비용 변수간의 상관분석을 수행하였으며, 모든 설명변수 간 상관계수가 0.6 이상으로 높은 선형적 상관관계가 존재함을 확인하였다. 그러나 통행시간 및 통행요금은 주요 정책변수이므로 두 개 변수를 모형 수식 안에 포함시키는 방안을 모색하였다. 통행시간, 통행거리, 통행요금의 설명변수를 하나씩 모형에서 제거해 보았으며, 또 다른 측면에서는 통행요금 변수를 단위거리 당 요금 변수로 변형하여 상관관계가 매우 적으면서 행태적 설명에 의미가 있는 설명변수로 변형시키는 방법도 시도하였다. 추가적으로 설명변수와 효용 값의 비선형적 관계를 찾기 위해 로그함수를 포함한 다양한 함수 형태로 설명변수를 변형시켜가며 통계학적 설명력이 높은 모형을 찾고자 노력하였다.
이렇게 시도한 모형 중에 가장 논리적으로 적합하다고 고려하여 선정한 모형이 Model 2(Equation 4)이다. 단위거리 당 요금 설명변수를 자연로그 함수로 취한 것은 통행거리 당 요금이 한 단위 씩 증가할수록 경로 선택에 주는 영향이 감소하는 비선형적 관계가 더 통계학적 설명력이 높기 때문이다. 예로 거리 당 요금이 10,000원인 경로와 1,000원인 경로에서 거리 당 요금이 각각 1,000원 씩 증가할 때 경로 선택 행태 변화는 거리 당 요금이 1,000원인 경로보다 보다 10,000원인 경로가 더 적은 현상을 설명하는 함수적 형태이다. 이와 같은 설명변수의 변형은 Lee et al.(2020)의 연구에서도 시도되었던 방법이다. 또한 통행시간 대신에 통행거리를 Model 2에 포함시킨 것은 통행시간을 포함시킨 모형보다 통계적 설명력이 좋을 뿐 아니라 논리적인 부호가 분석 결과로 나왔기 때문이었다. 이것은 중장거리의 경로 선택행태에 있어 교통상황에 따라 시시각각 변화할 수 있는 통행시간보다는 통행자들이 통행거리에 더 의미를 두고 선택행태를 자료에서 설명하고 있다고 해석이 가능할 것이다. 이렇게 선정한 Model 2의 경우 모든 독립변수가 95% 신뢰수준에서 통계적으로 유의하였으며 변수의 계수 값의 크기와 부호 또한 논리적이다.
경로 선택 행태에 영향을 줄 수 있는 요소 중 하나는 각 경로의 특성인 도로 위계가 있다. 고속도로와 같이 도로기능의 위계가 높은 수준의 도로는 장거리의 고속주행 통행이 활용하도록 계획되고 건설되고 있으므로 당연히 통행자들은 경로를 선택할 때 도로기능 위계를 고려하며 경로를 선택할 것이다. 그래서 본 연구는 대안 경로 상에 고속도로 구간이 포함되는 거리 또는 비율을 모형에 포함시켜보며 그 통계적 설명력을 검증하여 보았다. 이것은 Frejinger et al.(2006) 연구에서도 도로의 위계가 경로 선택 행태에 중요한 영향을 주고 있다는 연구 결과와도 같은 의미를 갖는 내용이다.
이와 같이 고속도로 경로가 경로 선택행태에 영향을 주는 형태를 찾아가는 과정에서 최종적으로 경로 내 고속도로 비율보다는 실제 이용거리가 더 통계적 설명이 높다는 분석결과가 도출되었으며 최종적으로 Model 3이 구축되었다. Model 2에 추가적으로 경로 내 고속도로 통행거리()변수를 모형에 포함시킬 경우 Table 3에서 볼 수 있듯이 모든 설명변수의 계수 값 크기, 부호, t-value가 논리적이며 통계적으로 유의하였다. Model 3의 모형정산 결과에서 경로 내 고속도로 통행거리 변수의 계수가 양의 값으로 정산되었으며, 이는 통행자들이 특정 대안 경로에서 고속도로 구간의 길이가 더 길수록 해당 경로를 더 선호하는 행태를 설명하고 있는 것이다. 모형의 전체적인 통계적 설명력인 값을 비교해보면 Model 3의 값이 Model 2의 값 보다 소폭 증가하여 추가적 설명변수를 포함함으로서 오는 자유도 손실에 비해 모형 전체적인 설명력은 조금 향상되었다.
Model 2에 경로 내 고속도로 통행거리()변수를 추가했을 때 모형의 설명력이 통계적으로 더 향상되어 좋은 모형이라고 판단할 수가 있는지를 검증하기 위해 Ben-Akiva and Lerman(1985)이 설명한 우도비 검정(Log-likelihood ratio test)을 수행하였다. 우도비 검정은 대안의 제약되지 않은 모형(Unrestricted model) 보다는 제약된 조건의 모형(Restricted model)이 더 좋은 모형으로서 참의 모형이라는 가정의 귀무가설을 검정하는 방법이다. 위 검정은 카이제곱분포를 따르므로 두 모형의 값을 이용하여 값을 산정한다. 그리고 자유도와 신뢰수준으로 임계값(Critical value)를 산정하여 값과 비교하고 귀무가설 채택여부를 판단한다. 우도비 검정에서 의 산출식은 Equation 6과 같다.
Model 3는 Model 2에서 설명변수가 변수 한 개만 증가하였으므로 자유도는 1이 되며 이에 해당하는 95% 신뢰수준 값의 임계값은 3.84이며, Equation 6에 의해 계산된 값은 171.2이다. 우도비 검정 결과에서 값이 임계값보다 훨씬 크므로 높은 통계적 확신을 갖고 귀무가설을 기각할 수 있다. 이것은 대안 경로 내 고속도로 길이를 설명변수로 추가할 경우 통계적으로 매우 유의미 하게 설명력을 향상시켜 Model 2에 비해 더 좋은 모형이라는 것을 의미하는 것이다. 이상과 같은 모형정산 과정을 거치면서 시도한 모형 중에 가장 통계학적 설명력이 높고 행태 설명이 논리적이라고 고려되는 Model 3 모형을 최종 경로 선택 행태모형으로 선정하였다.
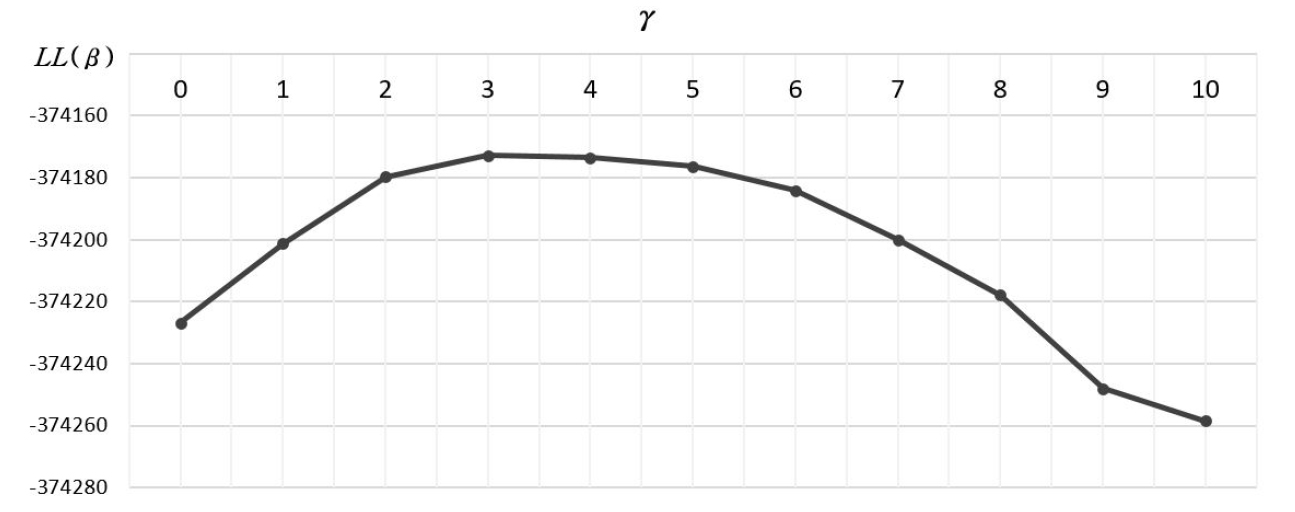
선행연구에서 언급한 것처럼 분석 네트워크나 자료에 따라 값은 상이할 수 있으므로 분석자의 논리적인 주관에 의해 설정될 수 있다고 하였다. 본 연구에서는 Model 3를 기준으로 내비게이션 자료가 경로 선택 행태를 가장 잘 설명할 수 있도록 PS 로짓 모형에 포함된 값을 추정을 분석하였다. 본 연구는 를 0에서 정수 값으로 점차 증가시키면서 모형 전체의 설명력을 표현하는 우도함수(Log-Likelihood function) 값 을 최대로 하는 값을 탐색하였다. 그리고 이 최대일 때의 값을 기준으로 하한 값과 상한 값 범주(interval)를 설정하고 황금분할법을 이용하여 범주 내 분석 간격을 좁혀가며 더욱 정확한 값을 탐색하였다. 이와 같은 황금분할법에 의해 탐색한 결과는 값이 3.427으로 도출되었다. Figure 1은 값의 변화에 따른 의 변화를 나타낸 것이다.
최종적으로 결정된 값으로 새로운 PS변수 산정하고 Model 3과 동일한 설명변수를 포함시켜 계수 값을 재추정한 경로 선택 모형은 Table 5와 같다. 동일한 설명변수를 사용하였음에도 불구하고 사용된 값에 따라 각 설명변수의 계수 값 크기에도 약간의 변화가 있음을 알 수가 있다. 이것은 대안 경로 간의 중복구간에 대한 반영 정도를 나타내는 값의 크기에 따라서도 설명변수와 효용의 관계에 영향을 받는다는 것을 의미하는 것이다. 값이 1인 Model 3의 정산결과와 같이 모든 설명변수의 계수 값 크기와 부호가 논리적으로 정산되었으며, 모든 설명변수의 P-value 값이 매우 높은 신뢰수준에서 통계적으로 유의하였다. 값을 3.427로 적용한 경우가 1인 경우보다 값도 더 좋게 분석 결과가 나왔다. 이것은 임의의 값을 적용하기 보다는 자료에 기반하여 추정된 값이 더 설명력을 향상시킬 수 있음을 보여주는 것이다.
Table 5.
The calibration result of final model ()
| Explanatory variable | Coefficient | Standard error | T-ratio | P-value | |
| -0.0041 | 0.0002 | -18.13 | 0.0000 | ||
| -0.4488 | 0.0089 | -50.70 | 0.0000 | ||
| 0.0031 | 0.0002 | 14.06 | 0.0000 | ||
| -0.2031 | 0.0062 | -32.55 | 0.0000 | ||
| 0.2043 | |||||
| 0.2043 | |||||
본 연구에서 최종적으로 구축한 경로 선택모형에 의한 통행자 행태는 통행거리와 단위거리 당 요금이 증가할수록 해당 대안 경로를 선택할 확률은 떨어지며, 고속도로 이용 구간이 긴 대안 경로일수록 선택 확률이 높아진다는 점을 설명하고 있다. 모형에 의하면 고속도로에 의해 경로가 길어질 경우는 고속도로 이용 선호와 통행거리 증가에 의한 비선호가 상쇄되게 경로 선택 행태에 영향을 주게 됨을 보여준다. 예로 설명하면 고속도로 이용거리 변수의 계수는 0.0031이며 전체 경로의 통행거리 변수의 계수는 -0.0041이므로 1km 당 고속도로 이용에 의한 선호와 통행거리 증가에 따른 비선호의 상호상쇄는 계수 값 차이가 되므로 고속도로 이용의 경우 상쇄된 효용 영향은 -0.0011가 된다. 반면에 일반 도로의 경우는 상쇄효과가 없으므로 통행거리가 1km 증가에 따른 효용 값에의 영향은 그대로 -0.0041이 되어 경로거리 증가가 주는 부정적 영향은 더 크게 된다는 것을 알 수가 있다. 그러므로 통행자는 고속도로 이용거리가 증가할 때보다 국도 이용거리가 증가할 때 더 민감하게 반응하는 현실적 현상을 모형이 설명하고 있는 것이다.
모형 정확성 검증
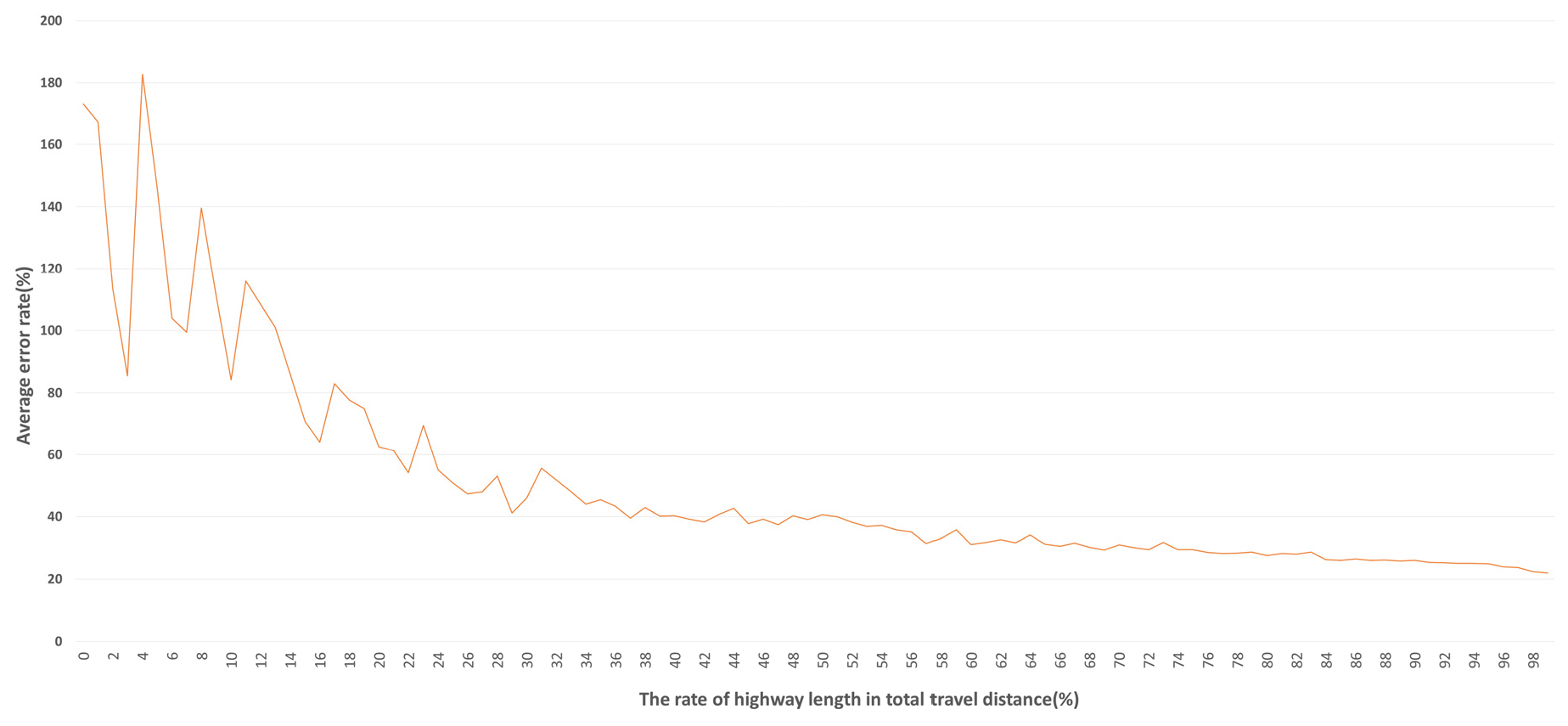
본 연구에서 최종적으로 정산한 경로 선택 모형의 예측 정확성을 검증하는 과정을 수행하였다. 연구에서 모형정산을 위해 사용한 자료는 2016년 7월 18-22일이며, 검증에 사용한 자료는 2016년 10월 17-21일에 수집된 자료이다. 검증에 사용된 내비게이션 10월 자료를 이용하여 자료 구축 방법과 같이 대안 경로 집합 구축하고 기종점 별 관측 통행량과 경로 별 통행거리, 통행거리 당 요금, 고속도로 이용거리, 관측 통행량을 산출하였다. 그리고 검증 자료에서 산출한 값들을 정산된 경로 선택 예측모형에 입력하여 경로 별 선택 확률을 예측한 결과와 경로별 관측 분담 비율을 분석 비교하였다. Figure 2는 고속도로 이용비율 별로 평균 오차율 규모를 나타낸 그래프이다.
정산된 예측모형으로 예측된 대안 경로 간의 분담률과 관측된 대안 경로 간 분담률 비교 분석 결과에서 모형의 예측 오차율은 20% 이상으로 나왔다. 또한 통행 경로에서 고속도로의 구간 길이 비중이 감소할수록 평균 오차율이 증가하며 오차율의 편차도 증가함을 알 수 있다. 이러한 분석결과는 기종점 통행에서 일반 도로의 이용 길이가 증가할수록 많은 대안 경로가 존재하고 그 경로 선택의 행태가 일관적이지 않아 모형으로 정확히 설명되기가 어렵기 때문이라고 고려된다. 이와 반대로 대안 경로 상에 고속도로 구간 길이의 비중이 증가할수록 경로의 예측 오차율이 감소하는 것은 그 대안 경로가 명확하며 대안의 수도 적기 때문이라고 고려된다.
모형 검증 결과에서 만족스러운 경로 선택모형의 예측 정확성을 보이지는 않지만 대안 경로 간 통행시간이 조금이라도 빠른 경로를 모든 통행자들이 선택한다고 가정하는 결정적 모형(Deterministic model)인 노선배정기법에 비해서는 좀 더 현실적 경로 선택 행태를 설명한 결과일 것이라고 고려된다. 그리고 기존에는 개별 통행자의 노선선택 행태를 자료의 한계로 인하여 설명을 할 수 없었지만 본 연구에서 내비게이션 자료를 사용하여 경로 선택 행태를 통행시간 뿐만 아니라 다른 요소들로 설명하였다. 또한 확률적 요소를 반영하여 좀 더 현실적 설명이 가능한 방향을 제시한 것은 의미가 있는 분석 결과라고 고려된다. 또한 내비게이션 자료 외에 경로 선택 행태에 영향을 주는 요소로써 통행자의 속성 및 경로의 서비스 속성들의 자료 수집이 용이하게 되고 모형 정산에 사용될 경우 그 모형 설명력은 더욱 향상될 수가 있을 것이라 예상된다.
결론
본 연구에서는 내비게이션 자료를 이용하여 통행자들의 실제 경로 기록을 대상으로 경로 선택모형을 구축하였다. PS 로짓 모형을 사용하여 공로 상의 다양한 경로가 존재함에 따라 발생하는 대안 경로 간 중첩되는 문제를 극복하였다. 내비게이션 자료는 자료수집 범위가 전국 모든 지역을 대상으로 기록되어 있어 매우 높은 표본수가 기록되어 있다. 특히 관측된 대규모 자료이면서 기종점 간 여러 대안 경로가 기록이 되어 있는 점은 경로 선택모형 정산에 매우 적절한 자료로 판단되었다. 기존 연구에서 소량의 표본자료를 이용한 모형구축에 불과하였던 점을 내비게이션 자료를 이용함으로써 더욱 현실성 있는 모형으로 정산할 수 있었다.
경로 선택 모형을 구축하는데 있어 기종점 집합화 및 대안 경로 집합 구축은 중요하다. 본 연구에서는 장거리 통행인 100km 이상 통행기록을 대상으로 시군구 단위 기준으로 기종점을 집합화 하였다. 기종점 집합화에 따라 대안 경로 설정 시 도로의 위계를 기준으로 대안 경로를 설정하였다. 장거리 통행에 대한 분석의 정확도를 향상시키기 위해 고속도로 및 도시고속도로를 기준으로 대안 경로를 분류하였다. 위 기준에 특정되지 않은 일반국도 이하 도로를 이용한 통행은 일괄적으로 동일한 1개 경로로 가정하여 대안을 설정하였다. 통계적으로 유의한 모형을 정산하기 위해 시도해본 결과, 정산된 경로 선택모형은 총 통행거리, 단위거리 당 요금, 고속도로 통행거리, PS변수가 통행행태를 설명하는 설명변수로 설정되었다. 총 통행거리, 단위 거리 당 요금, PS변수는 경로 선택 효용과 반비례관계, 고속도로 통행거리는 비례관계로 정산되었다. 그리고 황금분할법을 이용하여 PS 변수 내 최적의 값을 3.427로 도출하였다. 최종적인 PS 변수의 값을 이용하여 구축한 모형은 통계적으로 가장 우수하였으며 통행자가 장거리 통행에서 고속도로 이하 도로보다는 고속도로를 선호하는 경향이 잘 나타나 있다.
본 연구에서 정산한 모형의 정확성을 검증하기 위해 같은 연도에 수집된 다른 날짜의 내비게이션 자료를 이용하여 모형의 고속도로 이용비율 별 평균 오차율을 산정하였다. 통행경로에 고속도로 비율이 증가할수록 오차율이 감소하였다. 그 이유는 고속도로를 이용하는 경로는 대안 특정이 용이하며 대안 경로가 많이 없기 때문이다. 하지만 고속도로 이용비율이 감소할수록 대안 경로가 무수히 많으므로 선택 행태가 모형으로 정확히 설명되기 어려워 큰 오차율을 도출하였다.
각종 교통계획 정책분석에서는 대안 경로 간 통행시간이 조금이라도 빠르면 모든 통행자들이 빠른 경로를 선택한다는 결정적 모형인 사용자 균형 상태를 찾는 노선배정모형을 적용하고 있다. 이러한 비현실적 가정은 대안 경로 간의 확률적 선택배분이 되는 확률적 노선배정(stochastic traffic assignment)에 의해 현실적 가정으로 발전시킬 수가 있다. 그러나 확률적 노선배정인 로짓 모형은 비관련 대안으로부터 독립성 속성의 한계성과 대안 경로 생성의 어려움이 있어 정책분석에 적용할 수 없었다. 이러한 로짓 모형의 독립성 속성의 한계로 인하여 발생하는 대안경로 간 중첩현상문제(overlapping problem)를 극복하고자 PS 로짓 모형을 적용할 수 있으며 로짓 모형 기반의 확률적 노선배정인 다이알 알고리즘(Dial’s algorithm)의 한계점도 극복 가능할 수 있다. 따라서 본 연구에서 실측 경로자료인 내비게이션 자료를 활용하여 개발한 PS 로짓 모형 기반의 확률적 노선배정 모형은 네트워크 분석이 수반되는 교통계획의 다양한 정책분석에 좀 더 현실적 분석 결과를 제공할 수 있는 기초를 마련한 것이라 고려된다.
본 연구의 한계점으로는 내비게이션 자료를 이용하는 통행자의 교통수단을 명확하게 알 수 없어 수단 별 경로 선택 행태가 다른 점을 고려할 수 없었다. 또한 경로 별 통행요금을 일괄적인 승용차 요금으로 산정하고 민자 고속도로 요금을 적용하지 못한 한계점이 있다. 연구의 다른 한계점으로 중장거리 통행에 초점을 맞추어 연구를 진행하였으므로 고속도로와 도시고속도로를 이용하지 않는 통행경로들을 1개의 경로로 집합화하여 고속도로를 이용하지 않는 경로에 대한 선택 행태에 대한 고려가 부족하였다. 그러므로 향후 연구에서 위와 같은 통행요금과 경로들에 대해 좀 더 세밀한 검토가 필요하다. 또한 통행자는 단거리 통행에서 내비게이션을 사용하지 않는 경향이 있어 자료의 수가 부족하여 분석 결과가 왜곡될 수 있다. 그러므로 추가적인 단거리 통행에 대한 경로 선택 행태 연구를 위해서는 많은 양의 자료를 이용한다면 단거리 통행에 대한 경로 선택 행태 분석이 가능할 것이다.
장래에는 새로운 도로 인프라 건설 보다는 기존 도로들의 운영 및 관리의 중요성이 높아질 것이다. 본 연구의 결과를 활용하여 향후 도로 시스템 변동 시 통행자들의 경로 변동을 예측할 수 있을 것이며 도로 운영관리 정책의 의사결정에 도움을 줄 것으로 기대된다.