Real-time Traffic Incident Clearance Time Prediction by Latent Class with Random Effect: Approach for Applying Imbalanced Data

Songha Lee; Juneyoung Park

doi:10.7470/jkst.2024.42.3.370

Preview

Article

Journal of Korean Society of Transportation. 30 June 2024. 370-384
https://doi.org/10.7470/jkst.2024.42.3.370

Real-time Traffic Incident Clearance Time Prediction by Latent Class with Random Effect: Approach for Applying Imbalanced Data

비관측 이질성이 있는 잠재 계층별 실시간 교통사고 처리시간 예측 : 불균형 데이터 적용을 위한 접근

Songha LEE¹

Juneyoung PARK²^*

이 송하¹

박 준영²^*

¹The Ph.D. Course, Smart City Engineering, Hanyang University, Ansan 15588, Korea

²Associate Professor, Department of Transportation & Logistics Engineering/Smart City Engineering, Hanyang University, Ansan 15588, Korea

¹한양대학교 스마트시티공학과 석박사통합과정

²한양대학교 교통·물류공학과/스마트시티공학과 부교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/3.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

Minimizing the negative impacts of traffic crashes after they occur is crucial for transportation agencies. Especially, accurate traffic incident clearance time prediction, among post-traffic crash management strategies, can reduce congestion by evaluating the crash impact area and providing route guidance strategies on the predicted time. Currently, several approaches have been developed various methodologies for estimating traffic incident clearance time and explaining the relationship between the time and exploratory factors. However, most of the studies were conducted overseas, making it challenging to apply them to the Korean highway road segments, which have different geometric and traffic conditions, unlike the proposed methodology. Moreover, the previous studies utilized historical data rather than dynamic data and exploratory studies about the relationship between real-time characteristics and clearance time are limited. As such, for predicting accuracy with dynamic data, novel approach is proposed for combining latent class analysis with unobserved heterogeneity and boosting algorithms, addressing with various environmental factors. Furthermore, by implementing sampling techniques and explainable artificial intelligence to resolve the imbalance clearance time data with a long tail distribution, model performance was improved and reliable results were revealed. As a result, the latent class-based prediction model that synthesized the time data with unobserved heterogeneity showed the best performance, and spatio-temporal differences in real-time traffic characteristics, trucks, and lighting facilities were highly correlated with the time variables. In the future, the results are expected to more accurately predict the range of clearance times, which is insufficient compared to general traffic, and support the establishment of systematic traffic crash management strategies based on real-time traffic characteristics and history data.

Keywords

ensemble model

imbalanced data

latent class analysis with random effect

real-time data

traffic incident clearance time

신속한 교통사고 처리 대응을 통해 부정적인 영향을 최소화하는 것은 교통 기관에 매우 중요하다. 특히, 교통사고 대응 전략 중 정확한 사고 처리시간 예측은 사고 영향 범위를 평가하고 예측 결과에 따른 경로 안내 전략을 제공함으로써 사고로 인한 혼잡을 줄일 수 있다. 이를 위해 다양한 연구들이 수행되지만 대부분 국외 연구로, 제안하는 방법론과 다른 기하학적, 교통 조건을 가지고 있는 국내 교통환경에 적용하기에는 어려움이 있고, 동적 데이터보다는 과거에 집계한 이력 데이터를 활용하여 실시간으로 변화하는 교통 특성과 사고 처리시간에 관련된 탐색적인 연구는 제한적이다. 따라서 본연구는 다양한 환경요인을 고려하여 임의 효과를 가진 잠재 계층 분석과 부스팅 계열 알고리즘을 결합하여 실시간 사고 처리시간 예측 모형을 개발하였다. 또한, 긴 꼬리 분포를 가진 사고 처리시간 데이터의 불균형을 해결하는 샘플링 기법과 설명가능한 인공지능을 적용하여 모형 성능 개선 및 신뢰성 있는 연구 결과를 도출하였다. 연구 결과, 관찰되지 않은 이질성이 포함된 사고 처리시간 데이터를 합성한 잠재 클래스 기반 예측 모델이 가장 성능이 우수하였고 실시간 교통류의 시공간적 차이, 화물차, 미작동한 조명시설이 사고 처리시간과 높은 상관관계가 있음을 보여주었다. 이 연구 결과는 일반 교통류에 비해 부족한 사고 교통류의 다양한 사고 처리시간 크기를 더욱 정확하게 예측하고 실시간성 교통 특성 및 이력 자료를 기반으로 체계적인 교통사고 대응 전략 수립을 지원할 수 있을 것으로 기대한다.

키워드

앙상블 모형

불균형적인 데이터

임의 효과 기반 잠재 계층분석

실시간성 데이터

교통사고 처리시간

MAIN

서론
기존 문헌 고찰
1. 고속도로 사고 처리시간 관련 연구
2. 군집분석 기반 교통사고 처리 지속시간 관련 연구
3. 교통사고 처리 지속시간 분석을 위한 표본 관련 연구
4. 기존 연구와의 차별성
연구 방법론
1. 연구 프레임워크
2. 활용 데이터
3. 무작위 임의 효과가 포함된 잠재 계층분석
4. 긴 꼬리 분포(Long-tailed distribution)에 따른 샘플링
5. 실시간 사고 지속시간 예측 모형
6. 예측 성능 평가 및 모형 해석
연구 결과
1. 무작위 임의효과(Random effect)를 고려한 계층분석 분석 결과
2. 실시간 사고처리 시간 예측 모형 개발 및 평가
3. 실시간 사고처리 시간 예측 모형 해석 결과
연구 결론

서론

예측이 어려운 비 반복 정체인 교통사고는 도로 용량 감소, 2차 사고 발생 가능성 증가 등 사회·경제적으로 부정적인 영향을 초래한다. 신속한 교통사고 처리 대응을 통해 영향을 최소화하는 것은 교통 기관에 매우 중요하기 때문에 이와 관련된 교통안전 대응 전략 수립 및 실행하고 있다. 미국 플로리다 주 교통부는 사고 현장에 관리자가 도착한 후 90분 이내 사고 해결을 목표로 로드 레인저(Road Rangers)와 같은 현장 지원 서비스를 제공하거나 예상되는 사고 처리시간을 기준으로 사전 계획된 우회 경로를 교통사고 관리 시스템을 통해 주변 운전자에게 제공하고 있다(Li et al,, 2018; Haule et al., 2019).

교통사고 처리시간(Traffic incident clearance time)은 교통사고 발생 후 사고 현장이 정리되고 원래 교통류로 회복될 때까지의 시간을 의미하는데 검지 시간, 대응 시간 및 제거 시간까지 세 가지 시간으로 구성되어 있다(Lee et al., 2015). 이러한 시간을 바탕으로 운전자에게 경로 안내 및 우회를 위한 신뢰성 있는 안전 정보를 제공하기 위해서는 적시에 정확한 사고 지속시간을 예측이 필요하다. 사고 처리시간 추정 시, 콕스 비례 위험 모형(Cox proportional hazard model) 또는 가속 고장 시간 모형(Accelerated failure time model)과 같은 매개변수 모형을 이용하거나 최근에는 빅데이터 활용성이 높아져 다양한 데이터를 바탕으로 인공지능기법을 활용하고 있다(Hou et al., 2014; Li, 2015; Kuang et al., 2019; Wu et al., 2011). 또한, 사고 처리시간의 분석의 다른 중요한 목적은 사건 기간과 설명 요인 간의 관계, 즉 인과관계를 탐색하여 영향 요인을 이해함으로써 추가 사고 대응 전략을 개발하는 것이다. 교통사고와 같이 사고처리 시간은 관련 차량 수 및 유형, 심각도 등 인적요인, 차량 요인, 시설 요인, 환경요인 등에 영향을 받는다(Lee et al., 2015; Hojati et al., 2013; Hou et al., 2014). 특히, 실시간성 영향 요인 중 기상 조건이 사고 지속시간에 큰 영향을 미치는 것으로 확인되었지만(Nam and Mannering, 2000; Zeng et al., 2023), 실시간성 교통 특성이 미치는 영향을 평가한 연구는 아직 미비하다. 사고 처리시간 및 사고데이터는 관찰된 요인 외에 관찰되지 않은 요인까지 모든 요인의 복합적인 상호작용이 존재하는데, 이를 비관측 이질성(Unobserved heterogeneity)이라고 한다. 이러한 이질성을 가진 데이터를 기반으로 모형 구축 시, 요인 계수의 이분산성(Heteroskedasticity)으로 인해 부정확한 결과가 추론될 수 있다는 한계점이 있다(Chung and Kim, 2020; Mannering et al., 2016). 이에 본 연구는 관찰되지 않은 이질성이 포함된 국내 고속도로의 사고자료를 활용하여 데이터 내 잠재된 사고 특성을 기준으로 실시간 사고 처리시간 모형을 개발하고 사고 처리시간과 설명 요인 간의 관계를 해석하는 탐색적인 연구를 수행하고자 하였다.

기존 문헌 고찰

1. 고속도로 사고 처리시간 관련 연구

교통사고 처리 지속시간에 대해 예측하거나 모형을 구축하기 위해 다양한 방법론이 제안되었다. 과거에는 정적인 데이터를 활용하여 통계적 가설에 따른 사고 기간과 설명 변수 사이의 관계를 설명하기 위해서 주로 선형적인 모형을 이용하였다(Li et al., 2018). Nam and Mannering(2000)은 고속도로 사고 발생 후 감지/보고 시간, 대응 시간 및 사고 기간의 정리 시간을 분석하기 위해 감마 이질성이 포함된 와이블(Weibull) 분포를 가진 위험 기반 기간 모형을 개발하였다. 다양한 확률분포 가정할 수 있는 프레일티(frailty) 모형 기반으로 사고 지속시간과 정적 또는 실시간성 영향 요인 관계를 추정하였다(Chung and Kim, 2020; Zeng et al., 2023). 하지만 선형성을 가정하는 통계적 모형은 비선형적 관계를 해석할 수 없다는 제약이 있다(Li et al., 2018). 그래서 데이터의 복잡성이 증가함에 따라 의사결정 트리 및 분류 트리, 인공신경망과 같이 사전 가정 없이 복잡한 비선형 관계를 해결할 수 있는 기계학습 방법을 활용한 예측 방법론이 제안되었다(Wei and Lee, 2007; Park et al., 2016). Ma et al.(2017)은 미국 워싱턴 고속도로 1,366건에 대해 GBDT(Gradient Boosting Decision Tree)를 적용하였다. 그 결과, 다른 모형에 비해 예측성능이 높았고 시간당 교통량이 처리시간에 상대적으로 높은 영향을 준다고 하였다. Tang et al.(2020)는 사고패턴별 부스팅 알고리즘을 통해 처리시간을 예측하고 상대적 변수중요도를 도출하였다. Lee et al.(2015)는 사고 등급별 K-NN모형기반 사고 처리시간을 예측하였고, 연구 결과는 고속도로 돌발상황 발생 시 효율적인 고속도로의 운영관리를 지원할 수 있을 것으로 기대하였다.

2. 군집분석 기반 교통사고 처리 지속시간 관련 연구

교통사고는 복잡한 교통 메커니즘에서 무작위로 발생한 임의적인 상황으로 데이터 간 이질성이 존재하고 특정 패턴이 숨겨져 있어서 이러한 패턴을 식별하는 것이 교통안전 관리 전략 수립에 큰 영향을 준다(Depaire et al., 2008). Won and Chang(2019)는 사고 내 공통 특징을 기반으로 클래스별 사고 지속시간을 예측하는 방법론을 제안하였는데, 제안된 모형은 군집이 없는 모형에 비해 정확도가 높다고 평가하였다. 계량 경제학 모형인 무작위 매개변수가 포함된 잠재 계층분석과 생존 분석 모형을 결합한 결과, 전복 차량, 강우량이 사고 처리시간 증가시키는 요인으로 고속도로 순찰대 서비스를 활성화하여 처리시간을 단축할 필요가 있다 (Islam et al., 2021). 또한, 사고데이터 간 거리유사도를 기준으로 패턴을 탐색하였는데 기간 예측에는 지리적, 시간적 특성 외에도 공간적, 시간적 상관관계도 고려할 필요가 있다(Zhao et al., 2022; Tang et al., 2020).

3. 교통사고 처리 지속시간 분석을 위한 표본 관련 연구

교통사고는 일반적인 상황에 비해 예측할 수 없는 상황으로 교통사고 기간은 관찰할 수 없는 여러 가지 잠재적 요인을 포함하여 다양한 요인에 의해 결정되기 때문에 많은 표본을 이용하는 것이 중요해서 대부분의 연구는 수년간 누적되거나 대량의 사고데이터를 이용하였다(Khattak et al., 2012; Tang et al., 2020, Zeng et al., 2023). 표본 분석 시, 현실적으로 수집이 어려운 데이터는 교통 시뮬레이션을 통해 수집하여 사고로 인한 지연이 고속도로 네트워크에 미치는 영향을 정량화하기도 하였다(Jeihani et al., 2015).

4. 기존 연구와의 차별성

기존의 교통사고 처리시간 분석에 관한 연구들은 대부분 국외에서 수행된 연구로, 해당 방법론과 다른 기하학적, 교통 조건을 가지고 있는 국내 교통환경에 적용하기에는 어려움이 있다. 또한, 기존 연구에서 활용된 데이터는 주로 과거에 집계한 데이터와 실시간성 데이터를 제한적으로 사용하여 정확한 실시간 사고 지속시간 예측에 있어 제약이 있다. 그래서 본 연구는 사고 교통류에서 포착할 수 있는 징후 인자와 정형화되지 않은 사고 기록에 내포된 잠재 변인들까지 고려할 수 있는 다양한 유형의 데이터를 바탕으로 계층별, 샘플링 기법별 실시간 교통사고 처리 지속시간 예측 모형을 개발하고 영향 요인과의 관계를 해석하였다.

연구 방법론

1. 연구 프레임워크

본 연구는 다양한 유형의 교통사고 안전 지표 및 영향 요인이 포함된 국내 고속도로 사고자료를 기준으로 사고데이터 내 관찰되지 않은 이질성을 고려하기 위해 임의 효과(Random effect)가 포함된 잠재 계층분석과 부스팅 계열 알고리즘을 통해 처리시간을 예측하였다. 또한, 불균형적인 분포를 가진 사고데이터의 한계를 개선하기 위해 거리 유사도에 따른 데이터 합성 관련 샘플링 기법을 적용하였고, 마지막으로 설명가능한 인공지능을 이용하여 실시간 사고 지속시간과 설명 요인의 관계를 해석하였다(Figure 1).

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420308/images/kst_2024_423_370_F1.jpg

Figure 1.

Overall research framework

2. 활용 데이터

본 연구는 한국도로공사에서 관리하는 9개 노선(경부선, 영동선, 서해안선, 중부선, 제2중부선, 경인선, 제2경인선, 수도권 제 1순환선)의 2021년 사고자료 801건을 이용하였고, 데이터 특성에 따라 정적(Static) 데이터와 실시간성(Dynamic) 데이터로 구분하여 설명 요인을 수집 및 가공하였다. 정적 데이터는 고속도로 노선명, 이정명이 포함된 도로 기하구조 및 사고 세부 기록을 통해 인적요인, 환경요인 변수를 생성하였고, 사고 심각도, 사고 발생 위치, 사고 차량수, 사고 직후 상황 등을 연속형 또는 범주형으로 나타냈다. 그리고 실시간성 데이터는 루프 검지기 기반 교통류 데이터, 기상 데이터로 구성되어 있는데 시·공간적 데이터 연계 단위는 관련 문헌들을 검토하여(Yang et al., 2023), 5분/ 검지기 설치 간격 단위로 자료를 결합하였다. 사고 발생 전 교통류는 사고 위험예측 정확도에 직접적으로 영향을 미친다는 기존 연구 결과(Yang et al., 2023)를 참고하여 시공간적 교통 특성 차이에 의한 안전 지표를 산출하였다. 기상 정보는 고속도로 노선별, 이정별로 구분되어 있지 않아 기상관측소와 가장 근접한 고속도로 구간으로 데이터를 결합하였다. 본 연구에서 활용한 42개의 설명 변수와 종속 변수(사고 처리시간)에 대한 요약은 Table 1에 나타냈다.

Table 1.

Summary statistics of the exploratory variable

Variable	Description	Mean	S.D
Duration time	Traffic crash clearance time (minute)	49.25	60.25
Detection time	Traffic crash detection time (minute)	4.50	27.23
Response time	Traffic crash response time (minute)	12.73	10.37
Crash record and Road geometry (Static data)
Road type	Traffic crash occurred in tunnels, bridges, and ramps =1, otherwise =0	0.18	0.39
Lane	Number of lanes	4.21	2.38
length	length of segment (km)	5.36	4.07
Day	Night(18:00~06:00) is =1, Day(06:00~18:00) =0	0.34	0.48
Injury	Traffic crah with fatal and injury damage =1, otherwise =0	0.17	0.38
Num_veh	Number of vehicles in traffic crash	1.62	1.04
Weather	Weather condition including rainy, fog, snow =1, otherwise =0	0.40	0.49
Heavy_veh	The truck was involved: no = 0; otherwise = 1	0.36	0.48
Surface	Surface is not dry =1, otherwise =0	0.31	0.46
Light	Lighting equipment not working =1, , otherwise =0	0.11	0.31
Post-acc_stop	After the crash, there is a stopped vehicle	0.75	0.54
Post-acc_over	After the crash, there is a vehicle that overturned or rollover =1, otherwise =0	0.27	0.76
Traffic characteristic and weather condition (Dynamic data)
Rain_aws	Rainfall (mm)	0.68	2.42
Wind_spd	Wind speed	1.72	1.49
Humid_aws	Humidity(%)	64.33	31.81
Vol	Average traffic Volume at traffic crash occurrence (veh/5min)	134.66	113.53
Occ	Average occupancy at traffic crash occurrence (veh/lane/5min)	8.19	10.81
Speed	Average travel speed at traffic crash occurrence (km/h)	82.93	23.87
Tsd_5	Speed at the time point –	-4.09	20.21
Tsd_10	Speed at the time point –	-4.80	19.43
Tsd_15	Speed at the time point –	-7.83	22.59
Tvd_5	Volume at the time point –	13.79	77.88
Tvd_10	Volume at the time point –	-11.20	47.38
Tvd_15	Volume at the time point –	5.93	78.62
Tod_5	Occupancy at the time point –	1.60	7.865
Tod_10	Occupancy at the time point –	1.07	7.85
Tod_15	Occupancy at the time point –	2.02	8.22
Sod	Downstream occupancy –	20.68	115.88
Svd	Downstream volume –	2.79	10.71
Ssd	Downstream speed –	5.36	40.45
Tssd_5	Downstream speed at the time point –	4.43	41.37
Tssd_10	Downstream speed at the time point –	4.88	40.33
Tssd_15	Downstream speed at the time point –	3.42	41.63
Tsvd_5	Downstream volume at the time point –	27.76	118.91
Tsvd_10	Downstream volume at the time point –	15.16	117.89
Tsvd_15	Downstream volume at the time point –	25.93	120.01
Tsod_5	Downstream occupancy at the time point –	3.19	11.02
Tsod_10	Downstream occupancy at the time point –	2.90	10.85
Tsod_15	Downstream occupancy at the time point –	3.27	10.35

note: Mean means to the average statistic of each variable, and the standard deviation of each variable is appeared as S.D.

3. 무작위 임의 효과가 포함된 잠재 계층분석

복합적인 사고 영향 요인(예: 운전자 특성, 차량 상태, 도로 환경에 의해 발생하는 교통사고 데이터는 같은 기상 조건에서도 운전자의 운전 습관이나 경험에 따라 사고 발생 가능성이 다를 수 있으므로 특정 집단 내 특정 변수가 발생할 확률이 일정하지 않을 수 있다(Uebersax, 1999; Vacek, 1985). 이러한 한계점을 보완하기 위해 본 연구에서는 정규분포를 따르는 오차항이 포함된 잠재 계층분석을 활용하였고, 모형은 Equation 1, Equation 2과 같이 표현된다(Beath, 2017). Equation 1은 오차항이 존재하는 𝑖번째 데이터가 클래스 𝑐에 속할 확률을 구하는 과정으로 오차항 $λ_{i}$ 는 정규분포를 따른다고 가정한다. $π_{c i j}$ 는 𝑖번째 데이터가 클래스 𝑐에서 j번째 변수의 특성을 가질 확률을 프로빗 함수를 기반으로 표준 정규분포 형태의 확률값을 산출하는데 Equation 2와 같다. 이때, 잠재 계층분석은 명목형 변수만을 적용할 수 있으므로 ‘사고 차량 수(Num_veh)’ 변수는 계층분석 시에는 2대 이상 연관된 경우를 1, 단독사고인 경우를 0으로 변환하여 분석을 수행하였다.

(1)

P (y, \dots y_{i k} | c_{i} = c, λ_{i} = λ) = \prod_{j = 1}^{k} π_{c i j}^{y_{i j}} (1 - π_{c i j})^{1 - y_{i j}}

(2)

π_{c i j} = Φ^{- 1} (a_{c j} + b_{c j} λ_{i})

여기서, $y_{i j}$ : 𝑖번째 데이터의 𝑗번째 설명 변수가 가지는 값

$π_{c i j}$ : 𝑖번째 데이터가 클래스 𝑐에서 j번째 변수가 가질 확률

$c_{i}$ : 𝑖번째 데이터가 속한 잠재 클래스

$λ_{i}$ : 𝑖번째 데이터의 오차항으로 무작위 임의효과(Random effect)를 의미함

$Φ^{- 1}$ : 누적 표준 정규분포 함수의 역함수

$a_{c j}$ : 특정 클래스 𝑐와 결과 j에 대한 고정된 영향

$b_{c j}$ : 임의 효과를 조절하는 계수로, 사고데이터 간 분산

오차항 포함 여부에 따른 잠재 계층분 모형 적합도 평가 및 계층 수를 선택하기 위해 AIC(Akaike's Information Criteria), BIC(Bayesian Information Criteria) 지표를 종합적으로 활용하였다. AIC 및 BIC 값이 가장 낮은 계층 수를 가진 모형이 사고데이터에 적합한 모형이라고 평가하고 해당 지표는 Equation 3, Equation 4로 나타낸다(De Ona et al., 2013).

(3)

A I C = - 2 \log L + 2 P

(4)

B I C = - 2 \log L + P \times \log (n)

여기서, $L$ : 우도(Likelihood)

$P$ : 변수 개수

$n$ : 표본 개수

4. 긴 꼬리 분포(Long-tailed distribution)에 따른 샘플링

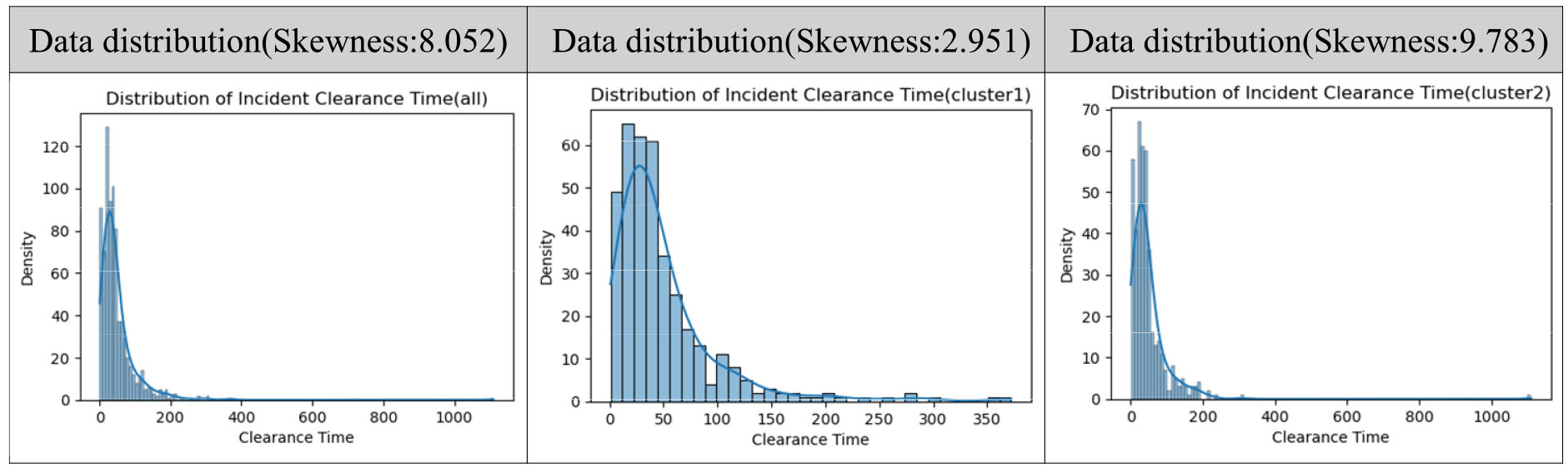
불균형적인 데이터로 인한 모형 성능과 관련된 문제는 주로 분류 예측(Classification)을 수행하는 연구들에서 언급하고 있지만, 회귀(Regression) 모형에서도 데이터 불균형 문제가 발생하는데 이는 정규분포를 따르는 이상적인 데이터와는 달리 데이터에 이상치가 포함되면서 분포의 비대칭성이 발생하는 것을 의미한다(Branco et al., 2016). 왜도(Skewness) 는 데이터 분포의 대칭성을 평가하는 지표로 해당 지표의 절대적 크기가 ‘0’에 가까울수록 중앙값과 평균값이 같은 정규분포를 가진다고 평가할 수 있고 크기 값이 ‘0.5’를 넘어가면 데이터의 편향이 있다고 판단할 수 있다(Yun and Bae, 2021). 평가지표를 기준으로 본 연구의 사고데이터 내 사고 지속시간의 데이터 분포 대칭성을 평가하였을 때, 절대적 크지는 8.052고 부호는 양수로 사고 처리시간은 오른쪽으로 긴 꼬리 분포를 하고 있음을 확인하였다(Figure 2).

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420308/images/kst_2024_423_370_F2.jpg

Figure 2.

Traffic incident clearance time data distribution and skewness value by latent class

이러한 문제를 처리하기 위해서는 훈련 데이터의 원래 데이터 분포를 변경하는 기법 적용이 필요하고, 해당 변수에 로그 함수를 취하는 방법과 달리 원본 데이터와 거리 공식을 활용한 새로운 값을 생성하는 오버샘플링 방식을 사용하고자 하였다(Yun and Bae, 2021). 본 연구에서 활용한 샘플링 기법은 무작위 언더 샘플링과 SmoteR 및 가우시안 노이즈 (Gaussian Noise) 을 결합한 SMOGN을 활용하였다(Branco et al., 2017). 제안하는 방법론은 SmoteR 모형을 기초로 데이터 합성이 되는데, SMOTE 알고리즘과 유사하게 데이터 간 거리유사도를 기반으로 Equation 5을 기반으로 종속 변수가 증강된다. 본 연구에서는 Python을 통해 종속 변수를 증강하였는데, 하이퍼파라미터는 기존 연구를 참고하여 데이터 유사성을 결정하는 파라미터 ‘k’와 가우시안 노이즈의 변동성을 나타내는 pert, 샘플링 방법을 지정하는 파라미터인 ‘samp_method’를 조정하여 구현하였다(Yun and Bae, 2021).

(5)

\hat{x} = x + λ (x_{n} - x) + N_{g} (0, σ^{2})

여기서, $\hat{x}$ : 합성된 데이터 샘플

$x$ : 극단 값을 가진 표본

$x_{n}$ : 데이터 x 주변에 있는 표본

$λ$ : 0과 1사이의 랜덤 값

$N_{g}$ : 가우시안 노이즈로, 해당 값은 정규분포를 따름

5. 실시간 사고 지속시간 예측 모형

계층별, 샘플링 기법별 실시간 사고 지속시간 예측 모형을 개발하기 위해 앙상블 계열의 3가지 기계학습 방법론을 활용하여 사고 처리시간을 예측하였고, 가장 성능이 우수한 모형을 기준으로 사고 처리시간과 관련 영향 요인과의 관계를 해석하였다.

1) Extreme Gradient Boosting(XGBoost)

XGBoost 알고리즘은 2016년에 개발된 라이브러리로 기존 그래디언트 부스팅(Gradient Boost Model) 알고리즘의 데이터 처리 시간 및 과적합 문제를 개선한 부스팅(Boosting) 계열의 모형으로, 본 논문에서는 이 알고리즘의 회귀함수를 이용하였다(Chen and Guestrin, 2016). 부스팅 알고리즘은 여러 개의 약한 학습기(weak learner)를 순차적으로 결합하고 가중치를 부여함으로써 강한 학습기를 생성한다. 또한, XGBoost 알고리즘은 훈련 손실함수와 모형의 복잡성을 제어하는 정규화 요소가 포함된 목적 함수를 바탕으로 병렬 학습이 가능하고 속도 처리가 기존 알고리즘에 비해 향상되었다. 하지만, 표본 데이터가 적을수록 과적합이 발생할 수 있어서, 알고리즘 내 매개변수 설정이 중요하다(Tang et al., 2020). 본 연구에서는 XGBoost 알고리즘 내 ‘max_deth’ 파라미터는 7로, ‘n_estimator’는 150~200으로 설정하고 사고 지속시간을 예측하였다.

2) Random Forest

Random Forest 알고리즘은 훈련 데이터에 대한 무작위 표본이 중복하여 선택하는 붓스트랩(Boostrap) 샘플링을 통해 노이즈가 많은 데이터의 분산을 감소시키는 앙상블 계열의 모형이다. 이 모형은 이상치에 영향을 받지 않고 통계적 가정 없이 활용 가능하다는 장점이 있으나, 훈련 시 메모리 소모가 크고 고차원 데이터를 활용할 때 모형의 성능이 저하될 우려가 있다(Yang et al., 2023). 또한, 하이퍼파라미터에 따라 모형 성능이 달라질 수 있어 본 연구에서는 트리의 개수를 나타내는 ‘n_estimators’는 200~300으로 설정하고 트리의 최대 깊이인 ‘max_depth’는 5로 설정하였다.

3) CatBoost

CatBoost(Prokhorenkova et al., 2017)는 순서 기반 부스팅 알고리즘으로, XGBoost 및 LightGBM과 비교하여 카테고리 기능을 효율적으로 처리하고 예측 변화를 효과적으로 해결하는 주요 이점이 있다. 기존의 부스팅 모델이 일괄적으로 모든 훈련 데이터의 잔차를 계산함으로써 모형 성능을 개선했다면, Catboost 모형은 훈련 데이터 일부만 계산하여 처리 속도가 개선되었다. 앞의 모형들과 같이 알고리즘의 성능을 결정하는 ‘n_estimators’, ‘depth' 두 가지 파라미터를 조정하였다.

6. 예측 성능 평가 및 모형 해석

계층별, 샘플링 기법별 실시간 사고처리 시간 예측 모형을 평가하기 위해 잠재 계층 적용 유/무, 데이터 합성에 따른 샘플링 기법 적용 유/무와 3가지의 예측 모형을 통해 총 9가지의 모형을 구축하였다. 모형별 성능 평가 및 최고 성능을 가진 모형을 찾기 위해 회귀 모형 평가 시 이용되는 MSE(Mean Squared Error), RMSE(Root Mean Squared Error), MAE(Mean Absolute Error), MAPE(Mean Absolute Percentage Error) 4가지 지표를 활용하였다(Yun and Bae, 2021; Zhao and Deng 2022).

모형 평가 시 가장 성능이 우수한 모형을 바탕으로 사고 처리시간과 설명 변수 간 관계를 해석하기 위해 설명가능한 인공지능 중 다양한 모델 유형(예: 트리 기반 모델, 신경망 등)에 적용할 수 있는 SHAP(SHapley Additive exPlanations)를 활용하였다. 직관적으로 해석이 가능한 통계 모형과 달리 기계학습 모형은 알고리즘 내에서 어떤 변수가 영향을 미쳤는지 확인이 어려운 Black-box 모형으로 이를 해석하려는 방법들이 고안되어왔다(Nandi and Pal, 2021). 다른 방법론들과 달리 게임 이론을 기반으로 인공지능 모형을 해석하는 SHAP 알고리즘은 Lundberg and Lee(2017)이 제안하였고, Equation 6에 의해 산출되는 Shapley Value의 조건부 기댓값에 따라 모델의 예측값 분해가 일관되게 이루어져 일관성 있는 해석이 가능하고 개별 예측에 대한 지역적 설명뿐만 아니라, 전체 데이터 세트에 대한 전역적 설명도 제공할 수 있다는 장점이 있다(Zou et al., 2023). 본 연구에서는 Python 패키지 중 SHAP 라이브러리를 사용하여 변수중요도 및 설명 요인과 사고 처리시간 변수와의 상관관계 확인하였다.

(6)

ϕ_{i} = \sum_{S \subseteq F / i} \frac{|S|! (|F| - |S| - 1)!}{|F|!} [f_{S \cup {i}} (x_{S \cup {i}}) - f_{S} (x_{s})]

여기서, $ϕ_{i}$ : i 번째 데이터에 대한 Shapley Value

$F$ : 전체 집합

$S$ : 전체 집합에서, i 번째 데이터가 빠진 나머지의, 모든 부분 집합

$f_{S \cup {i}} (x_{S \cup {i}})$ : i 번째 데이터를 포함한 기여도

$f_{S} (x_{s})$ : i 번째 데이터가 빠진, 나머지 부분 집합의 기여도

연구 결과

1. 무작위 임의효과(Random effect)를 고려한 계층분석 분석 결과

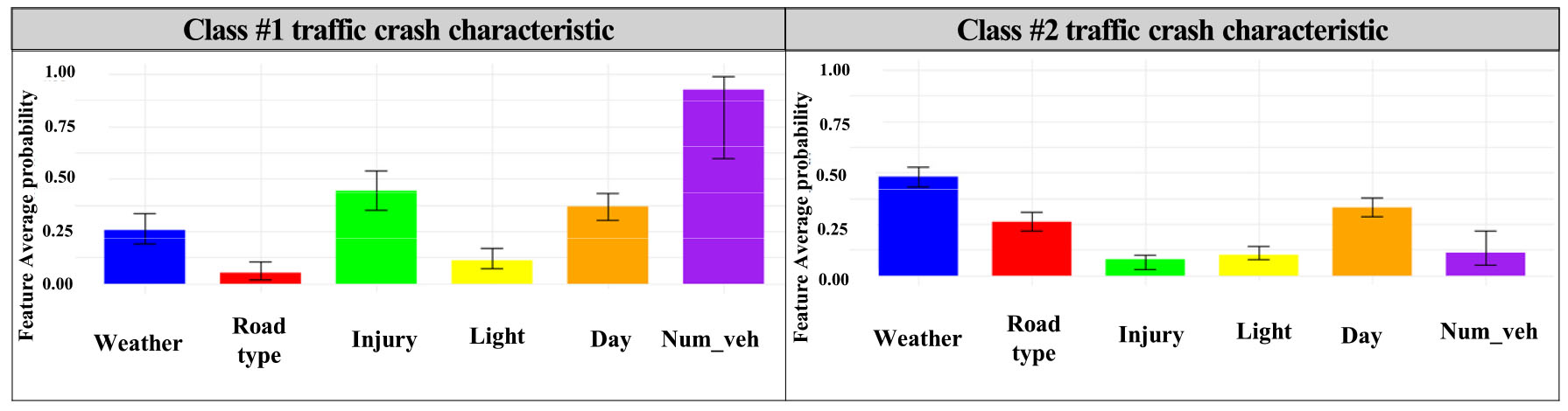
무작위 임의 효과 포함 여부에 따른 잠재 계층 분석 모형 설정 결과, 임의 효과를 가진 2개의 잠재 계층으로 구분하였을 때 모형 설정 평가지표 값이 BIC 지표 기준 4903.65로 가장 작았다(Table 2). 계층 개수별로 임의 효과 적용 여부를 비교하였을 때, 계층 구분 시 사고데이터 간 이질성을 고려하는 것이 모형 설정에 있어 성능이 우수함을 확인하였다. 이것은 여러 도로구간에서 복수의 시간에 걸쳐 누적된 사고데이터를 활용하였을 때 나타나는 이질성의 문제로, 모형 분석 시 수집된 데이터 외 설명되지 않은 요인을 고려할 필요가 있다(Mannering et al., 2016; Chung and Kim, 2020). Table 2의 계층 분석 결과를 바탕으로 도출된 이질성이 내포된 2개의 사고 잠재 계층별 세부 특성은 Figure 3과 Table 3에 나타냈다. Figure 3에 계층별 사고 특성을 나타낸 그래프는 각 사고 특성이 계층에 포함된 평균적인 크기와 신뢰구간의 상한선, 하한선이고 95% 신뢰구간 수준을 기준으로 나타냈다. 계층 1(Class #1)은 주로 고속도로 본선에서 부상자가 발생한 사고로, 최소 2대 이상 사고 차량수가 연관될 가능성이 높고 계층 2에 비해 야간 교통사고가 높은 비중을 차지하고 있음을 시사한다. 계층 2는 계층 1에 비해 강우 등 기상 조건에서 발생한 사고로 고속도로 본선 구간이 아닌 진·출입부, 터널이나 교량 등 도로 기하구조의 특징을 가지고 있다. 그리고 Table 3 중 계층 2(Class #2)의 ‘사고 차량수(Num_veh)’ 특성은 평균적으로 11.1%가 포함되어 있기에 해당 특성의 크기가 92.5 % 인 계층 1과는 달리 주로 차량 단독사고들이 포함되어 있다. 또한, 계층 1과 계층 2 모두 조명시설 요인의 확률값이 낮은 것을 확인할 수 있는데 이것은 주로 야간에 작동하는 조명시설이 미작동한 경우의 사고자료가 적기 때문에 나타난 결과로 Table 1에 나타낸 기초통계량 결과와 유사하다.

Table 2.

Results of goodness of fit for latent class analysis

Number of cluster	Latent class analysis without random effect		Latent class analysis with random effect
Number of cluster	AIC	BIC	AIC	BIC
Cluster 1	5045.03	5025.63	5029.33	5057.45
Cluster 2	4842.74	4988.99	4840.14	4903.65
Cluster 3	4856.00	4967.67	4842.73	4933.85
Cluster 4	4877.36	4974.36	4843.74	4969.26
Cluster 5	4891.53	5006.31	4849.38	5009.38
Cluster 6	4917.08	5023.77	4900.07	5038.06

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420308/images/kst_2024_423_370_F3.jpg

Figure 3.

Results of traffic crash characteristic by latent class analysis with random effect

Table 3.

Confidence interval on explanatory factors by latent class with random effect

Variable	Class #1 traffic crash			Class #2 traffic crash
Variable	Mean	2.5% CI	97.5% CI	Mean	2.5% CI	97.5% CI
Weather	0.255	0.188	0.338	0.479	0.432	0.526
Road type	0.053	0.028	0.105	0.260	0.217	0.309
Injury	0.444	0.354	0.538	0.032	0.008	0.109
Light	0.108	0.082	0.145	0.113	0.072	0.175
Day	0.367	0.304	0.435	0.332	0.289	0.377
Num_veh	0.925	0.593	0.990	0.111	0.053	0.217

note: CI means confidence interval

2. 실시간 사고처리 시간 예측 모형 개발 및 평가

실시간 사고 처리시간 예측 모형에 입력데이터를 적용하는 과정에서 이전에 수행한 잠재 계층분석 결과를 활용하여 계층이 없는 경우, 계층이 있는 경우로 구분하여 데이터 합성 샘플링 기법을 적용하였다. 예측 모형에 학습 및 검증을 위해 적용된 증강된 데이터의 크기는 Table 4에 나타냈고, 합성된 데이터와 원본 데이터 분포의 일부를 비교한 결과는 Figure 4와 같다. 계층이 없는 경우(No clustering) 학습용(Train) 데이터 560건을 SMGON 알고리즘을 적용하였을 때, 합성된 데이터는 총 487건이고 이때, 세부 파라미터는 ‘k’ 값은 5, ‘pert’은 0.1로 설정하였다.

Table 4.

Shape of dataset according to data augmentation

Dataset	Clustering	Raw dataset	Sampled dataset with SMOGN
Train	No clustering	560	1047(487)
	Class #1 with random effect	333	630(297)
	Class #2 with random effect	225	429(204)
Test	No clustering	241	629(198)
	Class #1 with random effect	143	255(112)
	Class #2 with random effect	100	189(89)

note: Raw dataset is original data and number of synthesized data in parentheses

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420308/images/kst_2024_423_370_F4.jpg

Figure 4.

Comparison of data distributions for original and augmented exploratory variables

Table 5는 계층 유/무, 샘플링 기법에 따른 모형 성능 비교 결과를 나타낸 것으로 샘플링 기법에 따른 성능을 비교하기 위해 기본 샘플링 기법(No Sampling)은 7:3 학습용/ 검증용 데이터의 분할을 의미한다. 또한, 하나의 평가지표만으로는 명확하게 검증하기 어렵기 때문에 세 가지 지표를 모두 활용하여 모형별로 예측성능을 정량적 평가하였으며(Yun and Bae, 2021), 계층이 있는 경우는 계층별 모형 성능의 평균값으로 나타냈다. 예측 결과, 가장 성능이 좋은 모형은 CatBoost 알고리즘을 기반으로 계층별 데이터가 합성되었을 때 RMSE 기준 29.997의 오차를 가지고 28.361%의 오차율을 가진다. 계층 유/무 모형 성능을 비교하였을 때, 계층이 없는 경우에 비해 계층별 데이터 미합성 시 오차가 증가하였다. 이는 계층별 사고 표본이 적어 설명력 있는 예측 모형 구축에 한계가 있다는 것을 의미한다.

Table 5.

Results of real-time traffic incident clearance time prediction model by class, by sampling techniques

Model	Clustering	Sampling	Evaluation
Model	Clustering	Sampling	MSE	RMSE	MAPE(%)
XGBoost	No clustering	No Sampling	1273.847	35.691	31.268
	Latent class with random effect	No Sampling	1444.38	38.005	38.961
	Latent class with random effect	Oversampling	1029.704	32.089	28.056
Random forest	No clustering	No Sampling	1352.621	36.778	33.884
	Latent class with random effect	No Sampling	1523.809	39.036	33.901
	Latent class with random effect	Oversampling	1081.357	32.884	31.208
CatBoost	No clustering	No Sampling	1162.059	34.089	33.075
	Latent class with random effect	No Sampling	1229.413	35.063	34.068
	Latent class with random effect	Oversampling	899.820	29.997	28.361

3. 실시간 사고처리 시간 예측 모형 해석 결과

예측 모형 중 가장 성능이 우수한 Cat Boost 알고리즘과 샘플링 기법(Oversampling)을 통해 예측된 계층별 실시간 사고 처리시간과 설명 변수와의 관계를 해석하였고, 분석 결과는 Figure 5, Figure 6에 제시하였다. Figure 5는 특성 중요도(feature importance)와 특성 효과(feature effects)를 결합한 것으로 x축 Shapley value 값이 양수일 때 빨간색으로 퍼져 있는 경우 사고 처리시간과 해당 요인은 양의 상관관계를 가지고 있다고 해석할 수 있다. 계층 1은 화물차, 시간적 교통류 차, 사고 차량 수, 현장 도착시간, 사고 직후 상황이 사고 처리시간 크기와 양의 상관관계가 있고, 계층 2는 화물차, 시간적 교통류 차, 조명시설 미작동이 상관관계가 있음을 의미한다. Figure 6은 특정 독립 변수가 설명 변수에 미치는 영향을 확인하기 위해 사용하는 것으로 계층 1의 경우, 관련 연구 결과와 유사하게(Zeng et al., 2023) 사고 직후의 정차된 차량으로 인해 시공간적 속도 차, 점유율 차가 발생하기 때문에 사고 발생 시 도로 상류부에 대한 운영방안 마련이 필요하다. 또한, 계층 2의 경우 화물차 사고 시 시공간적 속도 차가 증가할수록 사고 처리시간도 양의 상관성을 가진다고 해석할 수 있고 화물차 사고 다발 구간을 대상으로 집중적인 체계적인 사고 후 대응 전략 수립이 필요하다(Lee et al., 2015).

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420308/images/kst_2024_423_370_F5.jpg

Figure 5.

Results of summary plot by latent class crashes

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420308/images/kst_2024_423_370_F6.jpg

Figure 6.

Results of dependence plot by latent class crashes

연구 결론

본 연구는 다양한 교통 메커니즘 환경에서 발생하는 교통사고 영향 요인들의 특성을 고려하여 계량 경제학 관점의 임의 효과가 포함된 잠재 계층분석과 기계학습 관점의 부스팅 계열 알고리즘을 결합하여 실시간 사고 처리시간 예측 모형을 개발하였다. 또한, 긴 꼬리 분포 형태인 사고 처리시간 데이터의 불균형을 해결하기 위해 SMOGN 기법을 적용한 데이터 합성 관련 샘플링 기법과 기존 모형과의 비교평가를 수행하였고, 이에 대한 유효성을 검증하였다. 마지막으로 설명가능한 인공지능을 활용하여 실시간성 예측 모형 기반 사고처리 시간과 설명 변수 간 상관성을 해석함으로써 교통사고 대응 관련 안전 전략 수립을 지원하였다. 연구 결과, 잠재 계층분석에서 사고 차량 수, 기상 조건, 사고 발생 위치, 조명시설, 사상 사고 발생 여부가 통계적으로 95%의 신뢰수준으로 계층을 구분하는 주요 변수임을 확인하였다. 이는 잠재 계층분석과 위험 기간 모델링을 결합한 기존의 연구 결과와 유사하고 모델 적합성은 잠재 클래스 위험 기반 기간 모델이 관찰되지 않은 이질성을 설명하는 이점과 함께 고속도로 사고 기간 데이터를 모델링하는 유망한 도구가 될 수 있음을 시사한다(Islam et al., 2021). 또한, 일반 교통류에 비해 데이터가 적은 사고 상황은 다양한 처리시간 크기를 가지는데 정확한 처리시간 예측을 위해서는 부족한 사고 처리시간을 합성함으로써 모형 성능 개선 가능성을 평가하였다. 이러한 연구 결과를 현장 적용하기 위해서는 심층적인 연구가 필요하다. 마지막으로 실시간 교통류의 시공간적 차이가 사고 처리시간과 양의 상관성을 가지고 있음을 확인하였는데, 향후에는 통계적 모형을 기반으로 심층적인 인과관계를 추론할 수 있을 것으로 예상된다. SHAP 값 도표는 독립변수와 설명 변수 사이의 비선형 관계와 임곗값 효과를 나타내므로 SHAP 방법의 적용은 잠재적으로 지역 정책 결정의 품질과 정확성을 향상하는 데 도움이 될 수 있다(Yang et al., 2021). 따라서 본 연구에서 확인된 비선형 관계는 상황 기반 교통안전 관리 전략 수립을 지원할 수 있는 도구로 활용될 수 있다.

본 연구에서는 시·공간적 데이터 결합을 위해 2021년 고속도로 사고자료만 활용하였지만, 향후 더 많은 사고 표본을 확충한다면 더욱 신뢰성이 있는 결과로 발전할 수 있을 것으로 기대한다. 또한, 도로구간의 교통류 단위로 안전성을 평가하였지만, 향후 데이터 구득 범위가 확장됨에 따라 영상 데이터 등 수집된 개별차량 궤적과 교통사고 안전 지표를 결합하여 사고 발생 시 시공간적 사고 세부 영향권 예측 연구를 수행할 수 있을 것으로 기대한다.

Funding

This work was supported by National Research Foundation of Korea(NRF) grant funded by the Korea governmentMSIT). (No. 2022R1A2C1093424)

알림

본 논문은 대한교통학회 제90회 학술발표회(2024.03.28)에서 발표된 내용을 수정.보완하여 작성된 것입니다.

References

Beath K. J. (2017), RandomLCA: An R Package for Latent Class with Random Effects Analysis, Journal of Statistical Software, 81, 1-25.

10.18637/jss.v081.i13

Branco P., Torgo L., Ribeiro R. P. (2017), SMOGN: A Pre-processing Approach for Imbalanced Regression, In First International Workshop on Learning with Imbalanced Domains, Theory and Applications, 36-50, PMLR.

Branco R., Ribeiro P., Torgo L. (2016a), UBL: An R Package for Utility-based Learning, ArXiv Preprint ArXiv:1604.08079.

Chen T., Guestrin C. (2016), Xgboost: A Scalable Tree Boosting System, In Proceedings of the 22nd Acm sigkdd International Conference on Knowledge Discovery and Data Mining, 785-794.

10.1145/2939672.2939785

Chung Y., Kim S. (2020), Identification of Critical Factors for Crash Duration with Consideration of Unobserved Heterogeneity, J. Korean Soc. Transp., 38(6), Korean Society of Transportation, 536-546.

10.7470/jkst.2020.38.6.536

De Ona J., López G., Mujalli R., Calvo F. J. (2013), Analysis of Traffic Accidents on Rural Highways using Latent Class Clustering and Bayesian Networks, Accident Analysis & Prevention, 51, 1-10.

10.1016/j.aap.2012.10.01623182777

Depaire B., Wets G., Vanhoof K. (2008), Traffic Accident Segmentation by Means of Latent Class Clustering, Accident Analysis & Prevention, 40(4), 1257-1266.

10.1016/j.aap.2008.01.00718606254

Haule H. J., Sando T., Lentz R., Chuan C. H., Alluri P. (2019), Evaluating the Impact and Clearance Duration of Freeway Incidents, International Journal of Transportation Science and Technology, 8(1), 13-24.

10.1016/j.ijtst.2018.06.005

Hojati A. T., Ferreira L., Washington S., Charles P. (2013), Hazard Based Models for Freeway Traffic Incident Duration, Accident Analysis & Prevention, 52, 171-181.

10.1016/j.aap.2012.12.03723333698

Hou L., Lao Y., Wang Y., Zhang Z., Zhang Y., Li Z. (2014), Time-varying Effects of Influential Factors on Incident Clearance Time using a Non-proportional Hazard-based Model, Transportation Research Part A: Policy and Practice, 63, 12-24.

10.1016/j.tra.2014.02.014

Islam N., Adanu E. K., Hainen A. M., Burdette S., Smith R., Jones S. (2021), A Comparative Analysis of Freeway Crash Incident Clearance Time using Random Parameter and Latent Class Hazard-based Duration Model, Accident Analysis & Prevention, 160, 106303.

10.1016/j.aap.2021.10630334303495

Jeihani M., James P., Saka A. A., Ardeshiri A. (2015), Traffic Recovery Time Estimation under Different Flow Regimes in Traffic Simulation, Journal of Traffic and Transportation Engineering (English Edition), 2(5), 291-300.

10.1016/j.jtte.2015.08.001

Khattak A., Wang X., Zhang H. (2012), Incident Management Integration Tool: Dynamically Predicting Incident Durations, Secondary Incident Occurrence and Incident Delays, IET Intelligent Transport Systems, 6(2), 204-214.

10.1049/iet-its.2011.0013

Kuang, L., Yan, H., Zhu, Y., Tu, S., Fan, X. (2019), Predicting Duration of Traffic Accidents Based on Cost-sensitive Bayesian Network and Weighted K-nearest Neighbor, Journal of Intelligent Transportation Systems, 23(2), 161-174.

10.1080/15472450.2018.1536978

Lee S. B., Han D. H., Lee Y. I. (2015), Development of Freeway Traffic Uncident Clearance Time Prediction Model by Accident Level, J. Korean Soc. Transp., 33(5), Korean Society of Transportation, 497-507.

10.7470/jkst.2015.33.5.497

Li R., Pereira F. C., Ben-Akiva M. E. (2018), Overview of Traffic Incident Duration Analysis and Prediction, European Transport Research Review, 10(2), 1-13.

10.1186/s12544-018-0300-1

Li, R. (2015), Traffic Incident Duration Analysis and Prediction Models Based on the Survival Analysis Approach, IET Intelligent Transport Systems, 9(4), 351-358.

10.1049/iet-its.2014.0036

Lundberg S. M., Lee S.-I. (2017), A Unified Approach to Interpreting Model Predictions, Advances in Neural Information Processing Systems, 30, 4768-4777, Red Hook, NY, Curran Associates.

Ma X., Ding C., Luan S., Wang Y., Wang Y. (2017), Prioritizing Influential Factors for Freeway Incident Clearance Time Prediction using the Gradient Boosting Decision Trees Method, IEEE Transactions on Intelligent Transportation Systems, 18(9), 2303-2310.

10.1109/TITS.2016.2635719

Mannering F. L., Shankar V., Bhat C. R. (2016), Unobserved Heterogeneity and the Statistical Analysis of Highway Accident Data, Analytic Methods in Accident Research, 11, 1-16.

10.1016/j.amar.2016.04.001

Nam D., Mannering F. (2000), An Exploratory Hazard-based Analysis of Highway Incident Duration, Transportation Research Part A: Policy and Practice, 34(2), 85-102.

10.1016/S0965-8564(98)00065-2

Nandi A., Pal A. K. (2021), Interpreting Machine Learning Models: Learn Model Interpretability and Explainability Methods, Apress LP.

Park H., Haghani A., Zhang X. (2016) Interpretation of Bayesian Neural Networks for Predicting the Duration of Detected Incidents, J Intell Transp.

10.1080/15472450.2015.1082428

Prokhorenkova L., Gusev G., Vorobev A. et al. (2017), CatBoost: Unbiased Boosting with Categorical Features, ArXiv Preprint ArXiv:1706.09516.

Tang J., Zheng L., Han C., Liu F., Cai J. (2020), Traffic Incident Clearance Time Prediction and Influencing Factor Analysis using Extreme Gradient Boosting Model, Journal of Advanced Transportation.

10.1155/2020/6401082

Uebersax J.S. (1999), Probit Latent Class Analysis with Dichotomous or Ordered Category Measures: Conditional Independence/Dependence Models, Applied Psychological Measurement, 23(4), 283-297.

10.1177/01466219922031400

Vacek P.M. (1985), The Effect of Conditional Dependence on the Evaluation of Diagnostic Tests, Biometrics, 41(4), 959-968.

10.2307/25309673830260

Wei C. H., Lee Y. (2007), Sequential Forecast of Incident Duration using Artificial Neural Network Models, Accident Analysis & Prevention, 39(5), 944-954.

10.1016/j.aap.2006.12.01717303059

Won M., Chang G. L. (2019), Ensemble Model to Estimate Incident Clearance Durations using Sequential Partitioning Process and Robust Regression, Transportation Research Record, 2673(8), 554-566.

10.1177/0361198119842115

Wu W. W., Chen S. Y., Zheng C. J. (2011), Traffic Incident Duration Prediction Based on Support Vector Regression, In ICCTP 2011, Towards Sustainable Transportation Systems, 2412-2421.

10.1061/41186(421)24122097838

Yang C., Chen M., Yuan Q. (2021), The Application of XGBoost and SHAP to Examining the Factors in Freight Truck-related Crashes: An Exploratory Analysis, Accident Analysis & Prevention, 158, 106153.

10.1016/j.aap.2021.10615334034073

Yang Y., Yin Y., Wang Y., Meng R., Yuan Z. (2023), Modeling of Freeway Real-time Traffic Crash Risk Based on Dynamic Traffic Flow Considering Temporal Effect Difference, Journal of Transportation Engineering, Part A: Systems, 149(7), 04023063.

10.1061/JTEPBS.TEENG-7717

Yun G. R., Bae S. H. (2021), Analysis of Incident Impact Factors and Development of SMOGN-DNN Model for Prediction of Incident Clearance Time, Journal of the Korea Institute of Intelligent Transportation Systems, 20(4), 46-56.

10.12815/kits.2021.20.4.46

Zeng Q., Wang F., Chen T., Sze N. N. (2023), Incorporating Real-time Weather Conditions into Analyzing Clearance Time of Freeway Accidents: A Grouped Random Parameters Hazard-based Duration Model with Time-varying Ccovariates, Analytic Methods in Accident Research, 38, 100267.

10.1016/j.amar.2023.100267

Zhao H., Gunardi W., Liu Y., Kiew C., Teng T. H., Yang X. B. (2022), Prediction of Traffic Incident Duration using Clustering-based Ensemble Learning Method, Journal of Transportation Engineering, Part A: Systems, 148(7), 04022044.

10.1061/JTEPBS.0000688

Zhao Y., Deng W. (2022), Prediction in Traffic Accident Duration Based on Heterogeneous Ensemble Learning, Applied Artificial Intelligence, 36(1), 2018643.

10.1080/08839514.2021.2018643

Zou Y., Han W., Zhang Y., Tang J., Zhong X. (2023), Analyzing Freeway Traffic Incident Clearance Time using a Deep Survival Model, Journal of Transportation Engineering, Part A: Systems, 149(10), 04023101.

10.1061/JTEPBS.TEENG-7653

Journal of Korean Society of Transportation ISSN:1229-1366(Print) 2234-4217(Online) 대한교통학회지

Preview

Real-time Traffic Incident Clearance Time Prediction by Latent Class with Random Effect: Approach for Applying Imbalanced Data

ABSTRACT

MAIN

Figure 1.

Overall research framework

Table 1.

Summary statistics of the exploratory variable

(1)

(2)

(3)

(4)

Figure 2.

Traffic incident clearance time data distribution and skewness value by latent class

(5)

(6)

Table 2.

Results of goodness of fit for latent class analysis

Figure 3.

Results of traffic crash characteristic by latent class analysis with random effect

Table 3.

Confidence interval on explanatory factors by latent class with random effect

Table 4.

Shape of dataset according to data augmentation

Figure 4.

Comparison of data distributions for original and augmented exploratory variables

Table 5.

Results of real-time traffic incident clearance time prediction model by class, by sampling techniques

Figure 5.

Results of summary plot by latent class crashes

Figure 6.

Results of dependence plot by latent class crashes

Funding

알림

References