Determining the Spatial Ranges and Characteristics of Pedestrian Hot Spots in Seoul Using L-function and KDE

Junghyun Hwang; Joonho Ko

doi:10.7470/jkst.2024.42.3.313

Preview

Article

Journal of Korean Society of Transportation. 30 June 2024. 313-330
https://doi.org/10.7470/jkst.2024.42.3.313

Determining the Spatial Ranges and Characteristics of Pedestrian Hot Spots in Seoul Using L-function and KDE

L-function과 KDE를 이용한 서울시 보행교통사고 잦은 곳의 공간적 범위 설정과 특성 분석

Junghyun HWANG¹

Joonho KO²^*

황 정현¹

고 준호²^*

¹Ph.D. Course, Graduate School of Urban Studies, Hanyang University, Seoul 04763, Korea

²Professor, Graduate School of Urban Studies, Hanyang University, Seoul 04763, Korea

¹한양대학교 도시대학원 박사과정

²한양대학교 도시대학원 교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/3.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

This study aimed to undertake a comprehensive spatial analysis to delineate optimal spatial ranges for identifying frequent pedestrian crash locations. The analysis focused on pedestrian crashes that occurred within the seoul metropolitan government area between 2016 and 2022, selected due to its significantly high ratio of pedestrian fatalities compared to overall traffic accident fatalities among metropolitan jurisdictions. To investigate the spatial dependence among point patterns of pedestrian crash data, ripley's k-function and l-function were employed to analyze the degree of clustering by distance. The findings indicate that pedestrian crashes each year exhibited clustered patterns characterized by spatial dependence among individual crash points, with clustering evident within distances of 30.7 meters as indicated by the rate of increases in l-function values, gradually tapering off beyond this range. Furthermore, a similar analysis conducted on non-pedestrian crashes revealed clustering within distances of 35.7 meters, approximately 1.16 times the observed clustering range for pedestrian crashes. Based on the application of l-function selected results, which identified pedestrian crash hot spots, and reviewing the kernel density estimation within 5 meter increments up to a 50 meter radius, the total count of hot spots shows a gradual increase, with less than 10% within buffer radius of 30 to 35 meters. Beyond this distance, the rate of increase diminishes more steeply. Moreover, the results indicate that expanding the buffer radius includes accidents on adjacent roads. Therefore, selecting a minimum distance of 30 meters for hot-spot analysis is meaningful. Spatial analysis of pedestrian crash hot spots based on intersection, road width, and land use metrics revealed higher proportions of hot spots along secondary and tertiary roads compared to main arteries, with higher risk associated with unsignalized roads than signalized intersections. This underscores the necessity for ongoing pedestrian safety policies targeting residential roadways.

Keywords

hot-spot

kernel density estimation

pedestrian crash

ripley’s l-function

spatial analysis

본 연구는 보행교통사고 잦은 곳의 적정 공간적 범위 설정을 위해 보행교통사고에 대한 점 패턴 분석과 보행교통사고 잦은 곳의 공간적 특성을 분석하였다. 분석은 광역자치단체 중 전체 교통사고 사망자 대비 보행자 사망자 비율이 가장 높은 서울특별시의 2016년에서 2022년까지 발생한 보행교통사고를 대상으로 하였다. 보행교통사고 데이터의 점 패턴 간 공간 의존성을 분석하기 위해 Ripley의 K-function 및 L-function을 사용하여 거리별 군집화 정도를 분석한 결과, 각 연도별 보행교통사고는 개별 사고 간의 공간적 의존성을 지닌 군집화된 상태이며 공간적 패턴의 군집화는 30.7m 거리까지 L-function 값이 급격히 증가되고 그 이상의 거리에서는 서서히 완화되는 것으로 나타났다. 또한, 동일한 방법으로 차대차 및 차량단독 교통사고의 군집화를 분석한 결과는 35.7m의 거리로 나타나 보행교통사고의 군집 패턴보다 1.16배 큰 것으로 나타났다. L-function에 의해 선정된 결과의 적용 가능성을 Buffer 반경 5m에서 50m까지 5m 간격의 Kernel Density Estimation로 분석한 보행사고 Hot Spot을 통해 검증한 결과, Hot Spot의 총량은 Buffer 반경 30m~35m에서 10% 미만으로 완만하게 증가하고 있으며 해당 거리 이상에서 총량 증가폭은 더 완만해졌다. 하지만, Buffer 반경이 커질수록 인접도로의 교통사고를 포함하는 결과를 보여주고 있어 Hot Spot을 식별하는 최소 거리로 30m를 선택하는 것은 중요한 의미를 지닌다. 30m 반경 보행교통사고 잦은 곳의 공간적 특성 분석을 위해 교차로, 도로폭, 토지이용 등의 자료와 공간분석한 결과, 광로 및 대로 보다는 중로, 소로에서 보행교통사고 잦은 곳의 비율이 더 높으며, 교차로보다는 무신호 도로에서의 보행교통사고 위험성이 더 높은 것으로 분석되어 주거생활권 도로에 대한 보행안전정책이 지속적으로 추진되어야 함을 시사하고 있다.

키워드

사고잦은곳

밀도함수

보행교통사고

리플리의 L함수

공간분석

MAIN

서론
1. 연구의 배경 및 목적
2. 연구 범위 및 방법
선행연구
1. 국내·외 교통사고 위험지점 선정 및 개선사업
2. 선행 연구 고찰
3. 선행 연구와의 차별성 및 분석방법론 정립
점 패턴 분석(Point Pattern Analysis)
1. 서울시 보행교통사고 최근접 이웃 분석 : k nearest neighbors
2. 공간분포패턴 분석 : Ripley’s K-function, L-function
3. 집중도 분석 : Kernel Density Estimation(KDE)
4. 시사점 도출
공간적 특성 분석(Spatial Characteristics)
결론

서론

1. 연구의 배경 및 목적

우리나라의 자동차 1만대당 교통사고 사망자수는 연평균 8.4% 감소(2011년 2.4명/1만대 → 2021년 1.0명/1만대)하여, OECD 회원국 평균(2021년 기준, 1.0명) 수준으로 국가 교통안전도는 향상되어 가고 있다. 하지만, 교통사고 사망자 중 보행 중 사망자의 비율은 34.9%(2021년)로 OECD 회원국 평균 18.0%에 비해 약 2배 높은 수준이다(KoROAD, 2023). 정부는 보행자 중심 교통안전대책을 수립하고, 어린이보호구역 개선사업, 보행자우선도로, 안전속도 5030 등 다양한 도로교통안전 개선사업을 통해 보행안전 정책을 지속적으로 추진하고 있으나, 보행자 사망자 비율은 Table 1과 같이, 주요 선진국 대비 높은 비율을 지속적으로 유지하고 있다.

Table 1.

Road crashes: fatalities or pedestrian fatalities by country (Unit: Persons, %)

Year	Country	Fatalities [A]	Pedestrians fat. [B]	Proportion(%) [B/A]	Country	Fatalities [A]	Pedestrians fat. [B]	Proportion(%) [B/A]
2000	Finland	396	62	15.7%	United	3,580	889	24.8%
2010		272	35	12.9%	Kingdom	1,905	415	21.8%
2020		223	22	9.9%		1,528^P	352^P	23.0%
2000	France	8,079	838	10.4%	Japan	10,410	2,955	28.4%
2010		3,992	485	12.1%		5,828	2,016	34.6%
2020		2,541	391	15.4%		3,416	1,203	35.2%
2000	United	41,945	4,763	11.4%	Korea	10,236	3,764	36.8%
2010	States	32,999	4,429	13.4%		5,505	2,082	37.8%
2020		38,680^E	6,610^E	17.1%		3,081	1,093	35.5%

note : P (Provisional value), E (Estimated value)

source : OECD Stat Homepage (http://stat.oecd.org), 2022.11.29

교통사고 감소를 위해서는 사고가 많이 발생하는 위험지점(Black Spot or Hot Spot)을 선정하고 사고발생 요인 및 문제점을 진단한 후 개선계획을 수립하여 개선공사를 추진하여야 한다. 이러한 절차는 미국 HSM(Highway Safety Manual)과 호주 EBSP(Evaluation of the Black Spot Program)에서 제시하고 있고, 우리나라는 교통사고 잦은 곳 개선사업 등을 통해 교통사고 위험지점을 선정하여 개선사업을 추진하고 있다(AASHTO, 2010; BTE, 1995).

하지만 보행교통사고 만을 한정하여 볼 때, 개선사업의 첫 번째 단계인 Network Screening을 통한 위험지점 선정과정에서 사고건수, 사고율 등의 정량적 기준이 어린이보호구역사고다발지점 2건, 노인보행교통사고다발지점 5건 등 개선사업 테마별로 차이가 있고, 공간적 범위도 사업별로 반경 100m~300m로 차이가 있는 현실이다. 또한, 기존의 교통사고 잦은 곳 개선사업을 통해 보행교통사고 비율이 높은 곳을 대상지로 선정하여 위험지점을 개선할 수도 있지만, 2020년 서울특별시 교통사고 35,227건 중 차대사람 사고는 7,671건으로 21.8% 차지하나, 교통사고 잦은 곳 개선사업의 서울특별시 1,096개 관리지점의 전체 사고건수 11,421건 중 차대사람 사고는 1,447건으로 12.7%에 불과하여 개선사업에 선정될 확률이 낮은 현실이다(KoROAD, 2021).

이러한 수치는 보행교통사고 잦은 곳 선정을 위한 적정거리, 사고건수 등 기준 재정립의 필요성을 보여준다. 본 연구는 기존 사고위험도 선정방법론을 비교·분석하여 보행교통사고 예방 효과 극대화를 위한 보행교통사고 잦은 곳의 공간적 군집도와 해당 지점의 공간적 특성을 분석하여 최적의 보행교통사고 잦은 곳 선정 범위를 제시하고자 한다.

2. 연구 범위 및 방법

우리나라 광역 지방자치단체별로 교통사고 통계자료를 보면, Table 2와 같이 전체 사망자 대비 2019년~2021년의 3년간 전국 차대사람 교통사고 사망자수 비율은 35.5%이나, 서울특별시의 경우 차대사람 교통사고 사망자수 비율이 52.2%로 가장 높게 나타났다.

Table 2.

Road crashes: fatalities or pedestrian fatalities by region (Unit: Persons, %)

3Years(2019~2021)	Korea	Seoul	Daejeon	Busan	Gwangju	...	Jeon-nam	Chung- buk	Gyeong- buk	Sejong
Fatalities [A]	9,346	712	202	329	161	...	822	519	1,042	38
Pedestrians fat. [B]	3,318	372	105	154	73	...	246	152	303	6
Proportion(%) [B/A]	35.5%	52.5%	52.0%	46.8%	45.3	...	29.9%	29.3%	29.1%	15.8%

source : KoROAD TAAS Homepage (http://taas.koroad.or.kr), 2022.12.02.

따라서 차대사람 교통사고 사망자 비율이 높은 서울특별시를 공간적 범위로 2016년~2022년의 기간을 시간적 범위로 설정하여 분석하였다. 분석에 사용된 자료는 도로교통공단의 교통사고분석시스템에서 Hong et al.(2021)이 제시한 자바스크립트 기반의 웹크롤링을 통해 서울특별시의 2016년~2022년 기간 동안 전체 교통사고 공간데이터를 수집하였다. Figure 1의 연구흐름 같이 기존의 교통사고 다발지점 선정방법(Hot Spot Identification, HSID) 등을 검토하고, 보행교통사고를 대상으로 Ripley’s K & L-function과 Kernel Density Estimation(KDE) 등을 통한 점 패턴분석을 실시하여 보행교통사고 잦은 곳(Pedestrian Hot Spot, Ped-HS) 선정을 위한 최적의 공간적 범위를 도출하였다. 또한, KDE 기반의 Ped-HS_KDE를 대상으로 도로폭, 교차로, 토지이용 등 도로현황 데이터와 공간분석을 실시하여 Ped-HS_KDE의 공간적 특성에 대해 분석하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F1.jpg

Figure 1.

Research flow

선행연구

1. 국내·외 교통사고 위험지점 선정 및 개선사업

우리나라의 도로교통 안전개선사업은 점, 선, 면 단위로 관리지점을 선정하여 개선사업을 추진하고 있다. 일반적으로 점 단위 사업은 사고건수 위주로, 선 단위 사업은 사고건수와 기하구조 위주로, 면 단위 사업은 구역 전체의 사고예방을 목적으로 대상지를 선정하고 선정된 곳에 대한 시설을 개선하고 있다.

교통사고 위험지점을 선정하여 개선하는 대표적인 사업으로는 ‘교통사고 잦은 곳 개선사업’이 있다. 1987년 국무총리실 주관 ‘교통안전종합대책’의 첫 번째 과제로 선정된 이후, 1991년부터 2021년까지 해당 사업 개선공사 완료지점의 사고건수는 28.7% 감소, 사망자수는 45.1% 감소했다(KoROAD, 2022). 사업 대상지는 교차로에서는 차량 정지선에서 후방으로 30m 이내, 횡단보도는 차랑 정지선에서 후방으로 30m 이내, 시가지 단일로는 반경 100m 이내, 고속도로 및 기타 단일로는 반경 200m 이내에서 1년 동안 교통사고 발생건수 5건 이상(일반시 3건 이상)인 지점을 기준으로 관리하고 있다.

다음으로 『교통안전법』에 따라 2008년부터 시행된 ‘교통사고원인조사’ 및 ‘교통시설 안전진단사업’이 있다. 대상지는 교차로는 반경 150m 이내, 단일로는 도시지역 600m, 도시지역외 1,000m의 도로구간에서 3년 동안 사망사고 3건 이상이거나, 중상이상사고 10건 이상 발행한 지점을 대상으로 추진하는 사업이며 아직까지 전체적인 사업 효과분석 결과는 공표되지 않고 있다. 다음으로 『국가균형발전특별법』, 『농어촌도로정비법』에 의해 실시되는 지방부 도로에 대한 ‘위험도로 구조개선 사업’으로 지방부 도로의 종단경사, 편경사, 곡선반경, 차로폭 등 기하구조, 교통사고 심각도지수, 일교통량, 지자체 사업요구도 등에 따라 지점별 위험도를 평가하고 대상지점 우선순위를 선정하여 개선하는 사업이 있다(Korea MOIS, 2022a).

또한, 행정안전부, 경찰청 등에서 추진하는 테마형 보행교통사고 다발지점 개선사업으로 ‘스쿨존 내 어린이 교통사고 다발지점 개선사업’, ‘노인보행교통사고 다발지점 개선사업’ 등이 있으며, 해당사업은 사고 테마별로 반경 100m, 200m, 300m의 범위에서 사고건수 2건에서 5건 이상인 지점을 대상으로 하고 있다(Korea MOIS, 2022b).

이와 달리, 『도로교통법』, 『보행안전 및 편의증진에 관한 법률』, 『교통약자의 이동편의 증진법』 등에 의한 ‘어린이보호구역’, ‘노인보호구역’, ‘장애인보호구역’, ‘보행환경개선지구’, ‘보행우선구역’ 등은 교통약자의 통행빈도가 높은 지점을 대상으로 교통사고 예방적 차원에서 구역을 지정하고 관리하는 사업이다.

해외 사례로는 호주의 ‘Black Spot Program’(BSP)을 들 수 있다. 우리나라의 교통사고 잦은 곳 개선사업과 유사한 사업으로 교차로, MidBlock, 작은도로 구간에서 사고건수가 5년간 최소 3건 이상, 도로구간은 5년 동안 1km 당 연평균 0.2건 이상인 도로를 대상으로 사업을 시행한다(Australian Gov, 2022). 또한 구역 단위로는 잠재적인 교통사고 예방을 위해 영국의 Home-Zone, 일본의 커뮤니티존, 독일의 Zone 30 등의 사업이 추진되고 있다(Korea MOIS, 2013).

2. 선행 연구 고찰

선행 연구를 보면, HSID를 위해 Hot Spot(HS) 대상구간의 적정 범위를 선정하는 방법과 HS의 우선순위를 결정하는 방법에 대한 연구로 구분할 수 있다. 대상구간 적정 범위 선정을 위해 주로 Screening, Clustering, Crash Prediction 등의 3가지 기법이 사용되고 있고, 사고건수, 사고율, 사고심각도, 잠재개선편익과 같은 지표를 통해 위험지점의 우선순위를 결정하고 있다. 우리나라 교통사고 잦은 곳 개선사업 등은 Figure 2의 Screening Methods 방식의 사고건수 기반으로 사업후보 대상지를 관리하고 EPDO(Equivalent Property Damage Only) 등을 반영하여 개선사업의 우선순위를 결정한다.

HS 선정의 분할 방법론과 우선순위 결정방법론에 따른 유의미한 상관관계가 없으며, 도로구간의 특성에 따른 적정방법론 선정이 중요한 것으로 요약할 수 있다. 이러한 결과는 적정한 HSID를 통해 교통안전 측면에서의 공학적 개선안 제시와 올바른 정책결정 도출의 타당한 근거 제시를 위한 논거들로 사용된다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F2.jpg

Figure 2.

The concept of the screening method (Sliding Window, SLW)

선행연구는 HS 선정의 분할 방법론과 우선순위 결정 방법론을 혼합한 연구가 많다. Table 3과 같이 EB 및 통계적 분석 기법, KDE, 클러스터링 및 공간분석 기법, 동적 및 머신러닝 기법으로 구분되며, 이 중 EB 및 통계적 분석 기법으로 Cheng et al.(2005)은 HSID에서 SR, CI, EB 방법을 비교해 EB의 유의미함을 도출하였다. Ghadi et al. (2017)은 EB, ExEB, AF, AR 중 EB가 가장 우수함을 밝혔고, SC, CL, CTV, HSMsm 등 4가지 도로 분할 방법의 장단점을 분석하였다. Ghadi et al.(2019)은 SLW와 SPA 방법론을 비교하여, 저속 도시부 도로는 SPA, 고속의 도로는 SLW가 효과적임을 밝혔다. 또한 EB를 활용한 타당성 분석에서 저속의 도로는 AADT 요인이, 고속의 도로는 통행 속도의 분포가 사고에 큰 영향을 미친다는 결과를 도출하였다.

Table 3.

Summary of studies

Classification	Authors	Year	Spatial ranges	Study years	Method	Number of accident	Remark
EB and statistical analysis	Borsos et al.	2016		3 year	CF, CR, EB, PSI, CCR		Different result of measure
	Cheng et al.	2005		3 year	SR, CI, EB		EB is outperform
	Cui et al.	2021	Model based	3 year	SD	Model based	One expressway road
	Debrabant et al.	2018	1km²	6 year	SAM (PTM)	Model based	Large area
	Dereli et al.	2017	1km	9 year	NBR, PR, EB	Model based	Long distance
	Elyasi et al.	2016	5~10km	3 year	CF, CR, EPDO, EACF-EB	10(3 year)	Long distance
	Ghadi et al.	2019	Model based	3 year	Urban: SPA, Expressway: SLW / EB	Model based	AADT, Speed factor
	Ghadi et al.	2017	Model based	3 year	SC, CL, CTV, HSMsm, EB, ExEB, AF, AR	Model based	SC and EB are the best
	Washington et al.	2014		3 year	EPDO, QBR, NBR		EPDO
	Yang and Loo	2016	100m	6 year	CC, EX, EB	Model based	Land use impact EB
KDE, clustering, and spatial analysis	Baranyai et al.	2022	300m	3 year	KDE and AADT	Model based	One main road
	Flahaut et al.	2003	100m	5 year	SAM (LSA), KM	Model based	One main road
	Lee and Chang	2005	Model based	3 year	K-Means	Not defined	One expressway road
	Lee and Yu	2010	100m~300m	10 year	CRP	3	One expressway road
	Murat et al.	2017	Model based	Not defined	CA, SE	Model based	-
	Nam and Kang	2007	1km²	3 year	KDE	Not defined	Large area
	Song et al.	2019	300m, 1km grid	1 year	LSA, KDE, Network KDE	Model based	Getis-ord Gi*
	Yang et al.	2016	Model based	5 year	LSA, KDE	Model based	Getis-ord Gi*
Dynamic, machine learning	Chang et al.	2022	50m	8 year	XGBoost, SHAP		Fatal pedestrian crash
	Fan et al.	2019	Model based	Model based	ML (SVM), DNN	Model based	DNN is better
	Gregoriades et al.	2013		Not defined	BNs, VISTAa, DTA		Traffic flow, Apeed factor
	Lee et al.	2020	160~480m (272m)	5 year	SLW, CRP, DSL	Not defined	DSL is best
	Medury et al.	2016	40m	6 year	Dynamic-HSID, SLW	2	Smaller HS lengths

note : AADT(Annual Average Daily Traffic); AF(Accident Frequency); AR(Accident Ratio); ARI(Accident Risk Index); BNs(Bayesian Networks); CA(Cluster Analysis); CC(pure Collision Count); CCR(Critical Crash Rate); CF(Crash Frequency); CI(Conﬁdence Interval); CL(Constant Length); CR(Crash Rate); CRP(Continuous Risk Profile); CTV(Constant Traffic Volume); DNN(Deep Neural Network); DSL(Dynamic Site Length); DTA(Dynamic Trafﬁc Assignment); Dynamic-HSID; EACF-EB(Expected Average Crash Frequency with Empirical Bayes); EB(Empirical Bayesian); EPDO(Equivalent Property Damage Only); EX(Excess Collision Count); ExEB(Excess Empirical Bayesian); HSMsm(Highway Safety Manual segmentation method); KDE(Kernel Density Estimation); KM(Kernel Method); K-Means; LSA(Local Spatial Autocorrelation); ML(Machine Learning); NBR(Negative Binomial Regression); Network KDE; PR(Poisson Regression); PSI(Potential for Safety Improvement); PTM(Poisson-Tweedie Models); QBR(Quantile Binomial Regression); SAM(Spatial Autoregressive Model); SC(Spatial Clustering); SD(Spacing Distribution); SE(Shannon Entropy); SHAP(Shapley Additive Explanations); SLW(Sliding Window); SPA(Spatial Auto-Correlation); SR(Simple Ranking); SVM(Support Vector Machine); VISTAa(Visual Interactive Systems for Transport Algorithms); XGBoost

Elyasi et al.(2016)은 동적 분할된 도로 구간을 CF, CR, EPDO 등의 방법으로 분석하여 사고 위험이 높은 도로 구간을 판별하였다. Cui et al.(2021)은 포아송 이론에 근거한 SD를 기반으로 HS의 적정 거리와 건수를 선정하고 이를 베이징-하빈 도로에 적용하였다. Dereli et al.(2017)은 터키 도로의 2005년~2013년 교통사고를 1km 단위로 NBR, PR, EB 방법을 활용해 각각의 HS를 비교 분석하였다. Washington et al.(2014)은 EPDO와 분할 회귀 기법 등을 적용해 HSID를 선정하고 이를 EB 방법과 비교하였다. Yang and Loo (2016)은 교통사고와 주변토지이용 특성을 반영한 EB 분석을 통해 HS을 선정하여 토지이용과 사고유형의 관계를 확인하였다.

KDE, 클러스터링 및 공간분석 기법으로는 Flahaut et al.(2003)은 벨기에 59km 구간에서 SPA와 KDE를 적용하여 유사한 특징을 도출하였으나 SPA가 더 현실적인 결과임을 밝혔다. Nam and Kang(2007)은 부산의 음주운전 사고를 KDE로 분석해 주점 밀집 지역과 사고 빈도의 높은 상관성을 확인하였다. Baranyai et al.(2022)은 KDE와 AADT를 활용해 개선 가능성이 높은 HS를 선정하는 모델을 제시하였다. Murat et al.(2017)은 군집 분석과 SE를 활용해 HS별 위험 수준을 도출하였다. Lee and Chang(2005)은 사고 위험 지점 선정을 위해 K-Means를 사용해 기존의 균일 간격 방식과 비교·분석하고, 경부선 부산 방향에 적용해 효율성을 검증하였다. Lee and Yu(2010)는 CRP 기법을 활용하여 경부선 영천IC~언양JCT 구간을 분석하여, 기존 사고 잦은 곳 선정 지점과 유사한 결과를 도출하였고 선정 구간의 위험도를 산출해 개선 사업 시 우선순위를 제시하였다. Yang et al.(2016)은 서울시를 50m 그리드로 나누고 Getis-Ord Gi*를 사용해 우선순위가 높은 지점을 선정하고 KDE로 미시적 지점을 분석하는 방법론을 제시하였다. Song et al.(2019)은 로드킬 다발 구간에 대해 300m 및 1km의 Getis-Ord Gi* 분석과 일반 KDE 및 네트워크 KDE를 실시하여 구역 단위 분석보다 로드킬 다발 구간의 시각적 확인이 용이함을 확인하였다.

마지막으로 동적 및 머신러닝 기법으로 Medury et al.(2016)은 보행 교통사고를 위한 Dynamic-HSID를 제시해 기존 SLW 기법보다 더 많은 사고를 포함하는 HS를 선정하였다. Lee et al.(2020)은 DSL을 통한 HS 선정 기법을 제시해 샌프란시스코 도로교통사고 자료를 기존의 SLW, CRP 방법과 비교하고 시공간적 연관성을 분석해 HS의 정확성을 확인하였다. Fan et al.(2019)은 벡터 기반 학습과 신경망 이론을 적용해 기상 상태에 따른 실시간 HS를 예측하였다. Chang et al.(2022)은 XGBoost와 SHAP를 활용한 머신러닝 기법으로 보행 사망사고 지점의 장소적 특징에 따른 위험도를 예측하였다.

EB 등의 통계적인 기법은 위험지역을 식별하는 가장 효과적인 방법이다.(Elvik, 2007) 하지만, KDE, 클러스터링 및 공간분석 기법은 지리학에서 많이 사용되는 방법으로 개별 교통사고의 공간적 군집성을 판단하는데 유용하다. 이는 Tobler의 지리학 제1법칙 “모든 것은 다른 모든 것과 관련이 되어 있다. 그러나 가까운 것은 먼 것보다 더욱더 관련이 되어 있다”로 설명되며, 공간상의 한 지점에서 측정된 현상이 다른 지점에서의 측정값과 서로 관련이 있는 공간 의존성을 기반으로 분석한다. 이를 측정하는 방법은 일반적으로 점형 자료는 K-function, KDE, 면형 자료는 Moran’s I, LISA 등의 방법을 사용한다.

3. 선행 연구와의 차별성 및 분석방법론 정립

많은 연구에도 불구하고 전 세계 34개국 중 32개 국가의 HS 선정이 단순건수법에 의해 수행되며, HS의 공간적 범위도 30m, 100m, 150m, 200m, 250m, 300m, 500m, 1km 이상 등 다양하다(Aziz et al., 2022). 또한 대다수의 분석법이 고속도로와 같은 연속류 또는 교차로 간 거리가 긴 국도구간을 대상으로 HS를 선정하는 기법을 제시하고 있다.

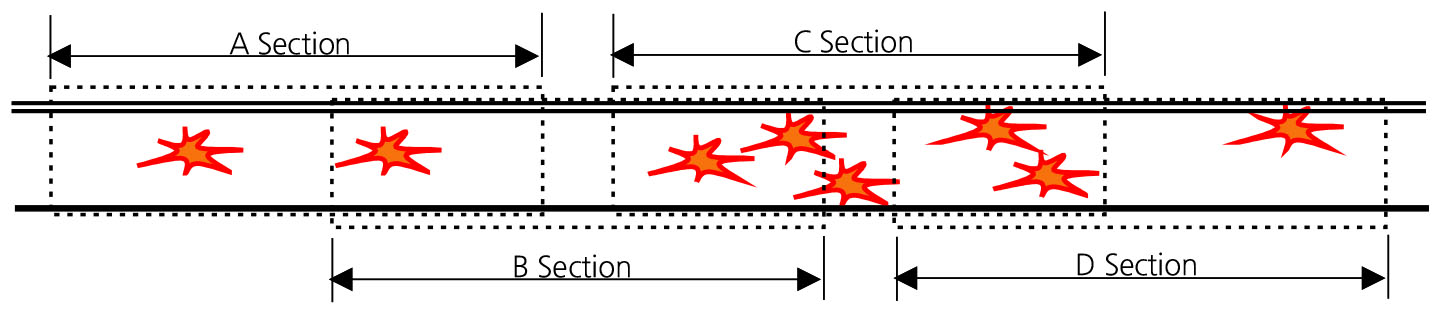
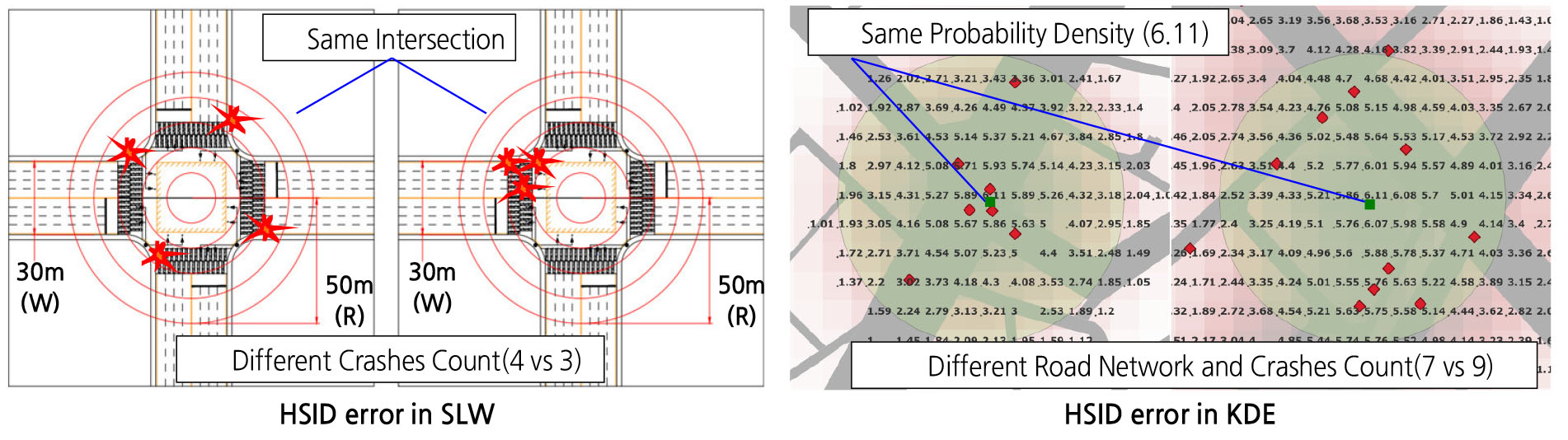
단순건수법에 많이 활용되는 SLW 또는 KDE의 경우, 도심의 복잡한 네트워크 망에서 HS 선정 시, 탐색반경에 따라 교통특성이 다른 두 개의 교차로가 인접한다거나, 연속된 두 개 도로구간을 포함하여 대상지가 선정되는 오류가 발생된다. 또한, Figure 3과 같이 SLW는 사고의 군집성보다는 특정 거리 이내의 단순 사고건수가 많은 곳에서 HS이 선정되며, KDE의 경우 탐색반경에 따라 확률밀도가 계산되어 다른 도로망에서 난 교통사고를 포함한 확률밀도 결과로 인해 HS을 판별하기 어려운 경우도 많다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F3.jpg

Figure 3.

Hot spot identification (HSID) error

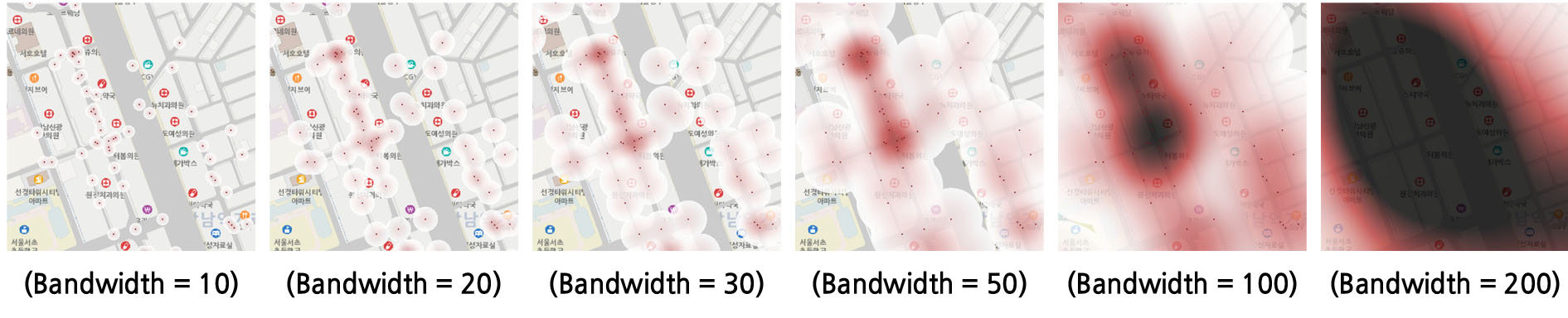
KDE는 HS를 시각적으로 확인하는데 유용하지만 통계적 유의성 검증에 어려움이 있다. Figure 4의 샘플과 같이 탐색반경인 평활계수(Bandwidth)가 작으면 적절한 HS를 선정하는데 한계가 있고, 탐색반경이 커질수록 인근 도로망 사고도 포함하는 확률밀도 값을 제시하여, 구도심의 복잡한 도로망에서는 부적절한 HS이 선정되는 문제가 발생한다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F4.jpg

Figure 4.

Sample heatmap (KDE) of Gangnam station by bandwidth

교통사고 HS 관련해서 사고밀집도와 위험지역에 관한 공간적 분석 연구는 많이 이루어져 왔다. 점형 데이터 분석인 K-function과 교통사고의 군집화에 대해서도 평면 및 네트워크 K-function을 적용한 Yamada and Thill(2004) 연구와 같이 다양하다. 하지만, 보행교통사고 간 군집에 기반한 HS의 적정거리에 대한 국내 연구는 미비하다. 앞선 Song et al.(2019)의 로드킬에 대한 연구도 국외 사례와 같이 향후 K-function의 적용 등 공간분석을 제언하고 있다. K-function을 통한 HS 선정 방법은 여러 이점이 있다. 우선 다양한 규모의 공간 관계를 분석하여 여러 거리에서의 클러스터링을 감지할 수 있다. 공간 패턴을 구분할 수 있어 사고가 집중되는 지점을 정확히 파악할 수 있다. 또한 공간 구조에 대한 민감도가 높아 HS을 정확하게 감지할 수 있다.

앞선 문제점을 종합해 보면, 연속류 도로와 달리 도심과 같이 신호교차로로 교통특성이 구분되는 단속류 도로에 대한 Ped-HS의 적정거리에 대한 기준 정립이 필요한 상황이다. 또한 구도심의 경우 교차로가 100m 이내로 서로 인접하여 위치한 교통특성을 가지고 있고, 보행자의 경우 교통상황에 인지반응하여 이동할 수 있는 거리가 짧은 특성을 지니고 있기 때문에 광범위한(Macro) 범위보다는 세밀한(Micro) 공간적 범위로 Ped-HS을 선정하는 연구가 필요하다.

이를 위해 점형 데이터인 교통사고 분포패턴을 지리학의 공간의존성 분석방법인 Ripley(1976)의 K-function과 L-function 등을 사용하여 포아송에 근거한 완전공간임의성(CSR, Complete Spatial Randomness)인 점패턴과 보행교통사고 분포패턴을 비교하였다. 이를 통해 어느 정도의 공간적 범위가 군집된 공간인지 균질한 분포인지에 대한 분석을 실시하고 보행교통사고가 군집되는 최소 거리를 제시하였다. L-fucntion에 의해 선정된 결과의 적용 가능성을 검토하기 위해, KDE를 통해 제시된 확률밀도 값을 기준으로 5m에서 50m까지 5m 간격의 Buffer 반경에 따른 Ped-HS_KDE를 선정하였고, Buffer 반경에 따른 Ped-HS_KDE의 총량 증가를 비교하였다.

분석된 결과를 바탕으로 서울특별시의 보행교통사고와 Ped-HS_KDE자료를 도로폭, 교차로 등의 도로환경 특성과의 공간조인을 통해 보행교통사고와 Ped-HS_KDE의 공간적 특성을 분석하였다.

점 패턴 분석(Point Pattern Analysis)

1. 서울시 보행교통사고 최근접 이웃 분석 : k nearest neighbors

서울시의 2016~2022년 전체 보행교통사고 자료를 대상으로 각 연도별 개별 교통사고 간 이격된 거리에 대해 분석하였다. 분석은 각 데이터 포인트에 대해 k개의 최근접 이웃을 찾는 k 최근접 이웃(k nearest neighbors) 방법을 사용하였다. 또한, 단속류 도로의 교통특성을 반영하기 위해 서울시 열린데이터광장의 6,765개 교차로 공간데이터(2021년말 기준) 간 평균 이격거리(128.2m)와 교차로 면적 등을 고려하여 개별 교통사고 간 거리가 100m 이내인 지점으로 구분하여 분석하였다.

교통사고 발생년도의 개별 i사고와 가장 가까운 거리에 있는 j사고를 k최근접 이웃(k=1)으로 하여 개별 보행교통사고의 최근접 사고 간 평균 거리를 계산하면, Table 4과 같이 각 연도별 전체 보행교통사고 위치 간 최단거리의 평균은 68.5m~90.5m이고 100m 이내 사고의 개별 사고 간 최단거리 위치 간 평균은 37.7m~42.7m로 나타났다.

Table 4.

Shortest distance between pedestrian crash positions: all pedestrian crashes vs pedestrian crashes within 100m (Unit: Numbers, m)

		2016	2017	2018	2019	2020	2021	2022
All Ped. Crashes	Num. of Crashes	10,683	10,249	9,978	9,896	7,671	7,075	7,807
	Average distance	68.5	72.2	70.8	72.5	86.1	90.5	86.0
	StDev.	76.9	77.5	82.0	84.0	89.6	89.7	93.6
Ped. Crashes within 100m	Num. of Crashes	8,209	7,762	7,564	7,416	5,294	4,656	5,343
	Average distance	37.7	39.1	38.5	38.6	42.7	42.4	41.7
	StDev.	27.7	27.1	27.0	26.9	28.0	28.0	28.3

source : Koroad TAAS (http://taas.koroad.or.kr), 2023.10.13

2. 공간분포패턴 분석 : Ripley’s K-function, L-function

Ripley’s K-function을 통해 개별 사고 간의 공간적 의존성을 분석하고, 점들이 군집되어 있는지 무작위로 분포되어 있는지 판단할 수 있다. 이론적으로는 포아송분포 등에 따른 규칙적인 점의 수와 일정 거리 내의 실제 분포하는 점의 수를 비교함으로써, 점이 군집되어 있는지 무작위로 분포되어 있는지 판정한다. K-function 곡선의 변곡점이 되는 지점은 개별 사고 간의 공간적 의존성을 지니는 지점으로 Equation 1로 표현한다.

(1)

K (r) = \frac{1}{λ N} \sum_{i} \sum_{j} I_{r} (d_{i j})

$K (r)$ : 거리 r까지 Ripley의 K값

N : R지역의 사고수

$λ$ : R지역의 사고밀도

$I_{r}$ : indicator( $d_{i j}$ ≦r인 경우 1, 아니면 0)

$d_{i j}$ : i사고와 j사고 간 거리( $i \neq j$ )

여기서 N은 R지역의 사고수이고, $λ$ 은 면적 R인 분석지역의 사고밀도로 N/R로 계산된다. ( $d_{i j}$ )는 두 점 사이의 거리 $d_{i j}$ 가 r보다 작으면 1, 아니면 0의 값을 지니는 판별지표이다. K(r)가 0인 경우, 관측된 패턴이 무작위 분포를 나타내고 K(r)가 양수인 경우에는 무작위 분포보다 더 밀집된 클러스터링 된 패턴으로 나타난다.

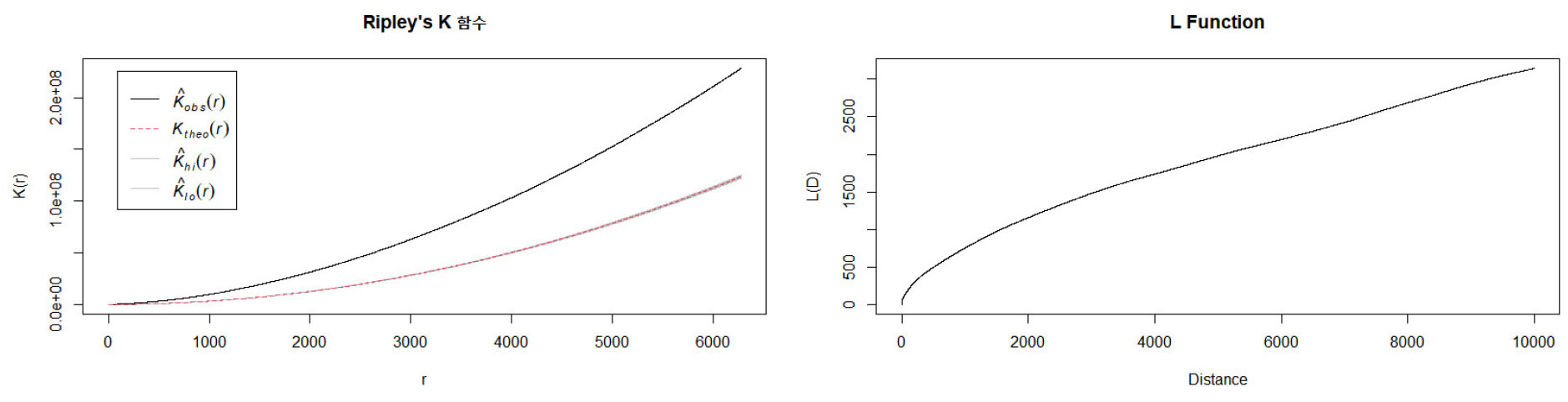
개별사고 간 공간적 의존성을 산출하기 위해 통계분석 패키지인 R을 이용하여 Ripley’s K-function, L-function 분석을 실시하였다. 여기서 K-function은 반경 내에 사고의 개수를 측정 분석하고, L-function은 특정 거리 내에 포함된 사고 간의 평균 거리를 측정하여 공간적 클러스터링을 분석한다. K-function의 결과는 반경 내 사고의 분포를 나타내고, L-function의 결과는 거리에 따른 사고의 평균 거리로 나타난다. 분석 결과, Figure 5와 같이 보행교통사고 데이터의 포인트 패턴 곡선인 ${\hat{K}}_{o b s} (r)$ 은 포와송분포에 근거한 CSR곡선인 ${\hat{K}}_{t h e o} (r)$ 보다 큰 값으로 나타나 개별 보행교통사고 간의 공간적 의존성을 지닌 클러스터링 된 상태임을 알 수 있다. 이러한 수치는 2016년에서 2022년의 모든 보행교통사고 데이터에서 동일하게 나타났다.

또한, K-function 값을 L-function으로 변환하여 공간 패턴을 분석할 수 있는데, 이는 특정 거리 내에 포함된 사고 간의 평균 거리를 측정하여 분석하는 방법으로 L-function를 통해 교통사고 데이터가 클러스터링 되어 있는지 시각화하여 비교할 수 있으며, Equation 2로 구해진다.

(2)

L (D) = \sqrt{\frac{K (D)}{π}} - D

D : 분석에 사용된 거리

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F5.jpg

Figure 5.

Pedestrian crash point pattern analysis by Ripley’s K-function and L-function in Seoul, 2022

2016년에서 2022년까지의 보행교통사고 점 데이터를 분석한 결과, L-function 그래프는 모든 연도에서 유사한 점 패턴으로 나타났고, 전체적인 군집성도 거리가 증가함에 따라 일정한 군집성을 유지하며 증가하는 것으로 나타났다. 개별 보행교통사고 간 세밀한 변화지점을 찾기 위해 100m 이하의 거리를 분석거리로 설정하고 L-function를 이용하여 Figure 6과 같이 보행교통사고와 차대차 및 차량단독 교통사고의 군집성을 시각화하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F6.jpg

Figure 6.

L-function plot between pedestrian crashes and non-pedestrian crashes

보행교통사고의 최소 군집성은 곡선의 변화율을 추정하는 방법을 적용하여, 거리(D) 값의 변화에 따라 L(D)의 값을 L(D-1)의 값과 비교하여 해당 점 곡선의 기울기가 상수에 가까워지는 거리(D)를 선정하였다. 기울기가 상수에 가까워지는 것은 기울기가 느리게 변화하는 구간을 의미하며 Figure 7 좌측 기울기 변화량 곡선의 잡음을 제거하기 위해 통계분석프로그램 R을 활용하여 비모수적인 회귀 분석 기법 중 하나인 lowess(LOcally WEighted Scatterplot Smoothing)를 통해 기울기가 안정적으로 형성되는 변화율의 절댓값이 0.05보다 작은 지점을 Figure 7 우측과 같이 추정하여 Table 5와 같은 결과를 도출하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F7.jpg

Figure 7.

Curve of change in slope and curve of smoothed gradient change rate, L-function plot 2022

Table 5.

The distance at which the smoothed rate of change in the gradient of L(D) for Ped. Crashes and Non-Ped. Crashes

Classification	Ped. Crashes							Non-Ped. Crashes
Classification	2016	2017	2018	2019	2020	2021	2022	2016	2017	2018	2019	2020	2021	2022
Distance	28m	34m	33m	32m	32m	31m	25m	36m	36m	37m	37m	36m	34m	34m

각 연도별 교통사고의 최소 군집거리 평균은 보행교통사고 30.7m으로 나타났고, 차대차 및 차량단독 교통사고는 35.7m로 보행교통사고에 비해 1.16배 큰 것으로 나타났다.

이러한 결과는 Ped-HS의 세밀한(Micro) 공간적 범위 설정이라는 연구 목적과 L-function에 따른 분석 값, 단속류 도로 특성 등을 고려할 때, 보행교통사고 HS의 최소 군집거리를 30m로 선택하는 것이 의미가 있음을 시사한다.

3. 집중도 분석 : Kernel Density Estimation(KDE)

KDE는 교통사고 분포 위치에 대해 단위 면적당 사고가 발생할 확률밀도로 산출하는 방법으로 확률밀도가 높은 지점은 단위 Kernel 당 사고 위험성이 높은 지점으로 나타난다. 이는 점 패턴의 공간적 집중도를 알아보기 위한 유용한 방법 중 하나로 HeatMap(열지도) 등으로 시각화되어 표현되며 일반적으로 Equation 3, 4로 구해진다.

(3)

\hat{f} (x) = \frac{1}{n} \sum_{i = 1}^{n} K_{h} (x - x_{i})

$\overset{⏜}{f} (x)$ : 추정된 확률밀도함수

$K_{h}$ : 확률밀도를 근사화하는데 사용한 가우시안 커널 함수

n : 데이터 점의 개수

(4)

K_{h} (x) = \frac{1}{\sqrt{2 π h}} \exp (- \frac{x^{2}}{2 h^{2}})

h : 평활계수(Bandwidth), 커널 함수의 반경을 결정

x : 데이터 점과 평가 지점 사이의 거리

서울시 보행교통사고 발생 지점에 대한 KDE는 공간분석프로그램인 Q-GIS를 활용하여 앞선 Figure 4에서 제시한 방법처럼 탐색반경에 따른 확률밀도를 HeatMap의 형태로 시각화할 수 있다. 적절하게 분석된 KDE는 도로망 주변으로 보행교통사고 위험지점의 확률밀도가 높게 나타난다. 하지만, KDE의 결과로 나타나는 HeatMap은 지도상의 래스터(사각형 등 격자)의 구조로 나타나며 교통사고가 많이 발생하는 곳을 진하고 흐린 정도로만 제시해 주고 정확한 HS의 개수와 위치를 제시해 주지 못한다.

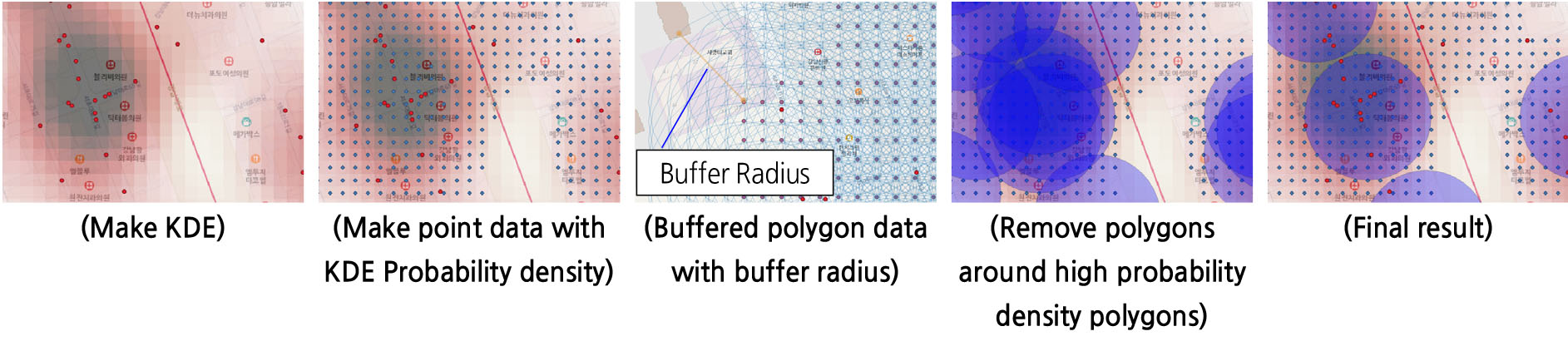
실무적으로는 HS_KDE선정은 Figure 8와 같이 KDE를 생성하고 산출된 확률밀도를 가진 모든 중심점을 Point로 생성하여 위치 및 속성데이터로 기록한다. 각각의 포인트를 중심으로 Buffer 반경의 Polygon으로 변환하고 가장 높은 확률밀도를 가지는 Polygon을 기준으로 영역이 겹치는 확률밀도가 낮은 주변의 Polygon을 제거한다. 반복적인 작업을 통해 독립적으로 남은 Polygon만을 HS_KDE로 최종 선정한다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F8.jpg

Figure 8.

Convert heatmap (KDE) data to buffered polygon data

앞 절에서 Ripley’s L-function에 의한 보행교통사고의 최소 군집거리를 선택하였다면, 이번 절에서는 KDE를 활용하여 Buffer 반경에 따른 Ped-HS_KDE를 생성하고 HS의 총량 증가에 따른 민감도를 검토하여 L-fucntion에 의해 선정된 결과의 적용가능성을 검증하고자 한다. 이를 위해 Figure 9와 같이 Buffer 반경을 5m에서 50m까지 5m 간격으로 증가시키며 Ped-HS_KDE를 산출하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F9.jpg

Figure 9.

Gangnam station Ped-HS_KDE sample by buffer radius, 2022

또한 각 연도의 Buffer 반경에 따른 Ped-HS_KDE의 총량 변화비율을 Equation 5와 같이 $R_{i}$ 로 정의하고 Buffer 반경에 따른 총량 증감률을 제시하였다. 산출된 결과는 Table 6과 같이 나타났다.

(5)

R_{i} = \frac{N umber of Ped ‐ {HS}_{i} - N umber of Ped ‐ {HS}_{i - 1}}{N umber of Ped ‐ {HS}_{i - 1}} \times 100

i = Buffer Radius Index

그 결과 분석 연도 별 Buffer 반경이 증가함에 따라 선정되는 Ped-HS_KDE의 총량도 증가한다. Buffer 반경 25m 이상에서 $R_{i}$ 가 약 20% 미만으로 증가하고, 30~35m 이상에서 $R_{i}$ 가 10% 미만으로 증가하였다.

KDE를 통한 Ped-HS_KDE 선정 시 Ped-HS_KDE 총량은 Buffer 반경 30m~35m에서 10% 미만으로 완만하게 증가하고 있으며 해당 거리 이상에서 Ped-HS_KDE 총량의 증가폭은 더 완만해지지만, Figure 9와 같이 Buffer 반경이 커질수록 인접 도로의 교통사고를 포함하는 HS이 선정되는 결과도 보여주고 있다.

Table 6.

Ped-HS_KDE containing 2 or more pedestrian crashes by year by buffer radius

Years Buffer radius		2016	2017	2018	2019	2020	2021	2022
Num. of All Ped. Crashes		10,683	10,249	9,978	9,896	7,671	7,075	7,807
5m (R₁)	Num. of Ped-HS	456(-)	290(-)	257(-)	270(-)	153(-)	112(-)	190(-)
10m (R₂)	Num. of Ped-HS	727(59.4%)	540(86.2%)	533(107.4%)	523(93.7%)	366(139.2%)	371(231.3%)	460(142.1%)
15m (R₃)	Num. of Ped-HS	1,283(76.5%)	1,075(99.1%)	1,079(102.4%)	1,027(96.4%)	633(73.0%)	573(54.4%)	706(53.5%)
20m (R₄)	Num. of Ped-HS	1,550(20.8%)	1,395(29.8%)	1,358(25.9%)	1,289(25.5%)	872(37.8%)	790(37.9%)	919(30.2%)
25m (R₅)	Num. of Ped-HS	1,808(16.6%)	1,654(18.6%)	1,645(21.1%)	1,549(20.2%)	1,040(19.3%)	938(18.7%)	1,051(14.4%)
30m (R₆)	Num. of Ped-HS	1,923(6.4%)	1,795(8.5%)	1,769(7.5%)	1,685(8.8%)	1,180(13.5%)	1,100(17.3%)	1,213(15.4%)
35m (R₇)	Num. of Ped-HS	2,072(7.7%)	1,930(7.5%)	1,910(8.0%)	1,828(8.5%)	1,291(9.4%)	1,196(8.7%)	1,292(6.5%)
40m (R₈)	Num. of Ped-HS	2,161(4.3%)	2,009(4.1%)	1,982(3.8%)	1,916(4.8%)	1,419(9.9%)	1,274(6.5%)	1,408(9.0%)
45m (R₉)	Num. of Ped-HS	2,199(1.8%)	2,039(1.5%)	2,040(2.9%)	1,971(2.9%)	1,483(4.5%)	1,337(4.9%)	1,445(2.6%)
50m (R₁₀)	Num. of Ped-HS	2,255(2.5%)	2,065(1.3%)	2,067(1.3%)	1,995(1.2%)	1,564(5.5%)	1,394(4.3%)	1,509(4.4%)

note : R_i = (Num. of Ped-HS_i — Num. of Ped-HS_i-1) / (Num. of Ped-HS_i-1) × 100, i = Buffer Radius Index

4. 시사점 도출

보행교통사고에 대한 Ripley's L-function 결과 값은 거리(D)가 증가할수록 더 많은 군집화가 이루어져 사고가 무작위 분포보다 더 빈번하게 군집되어 발생한다는 것을 의미한다. Ped-HS의 세밀한(Micro) 공간적 범위 설정이라는 연구 목적과 L-function에 따른 L(D) 값의 경미한 변동을 고려하여, 보행교통사고 HS의 최소 군집거리를 반경 30m로 결정하였다. 이를 KDE를 활용한 Ped-HS_KDE 선정 방법을 이용하여 검증한 결과, 30m~35m의 Buffer 반경에 따라 Ped-HS_KDE 총량이 완만하게 증가하는 것을 확인할 수 있었다.

Figure 10은 2022년 보행교통사고에 대한 KDE, Buffer 반경 30m의 Ped-HS_KDE와 Buffer 반경 50m의 Ped-HS_KDE에 대한 결과이다. KDE 결과는 도로망 주변으로 보행교통사고 다발지점에 대한 확률밀도가 높게 나타나는 것을 알 수 있으며, 대로보다는 보행자가 많은 중로 또는 소로 등의 도로망에서 보행교통사고의 밀도가 높은 것을 직관적으로 알 수 있다. 하지만, Buffer 반경 30m와 달리 Buffer 반경 50m의 Ped-HS_KDE에서는 인접 도로에서 발생한 보행교통사고도 동일한 지점의 Ped-HS_KDE에 포함됨을 알 수 있다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420305/images/kst_2024_423_313_F10.jpg

Figure 10.

Gangnam station KDE and Ped-HS_KDE (Buffer radius:30), errors of Ped-HS_KDE (Buffer radius:50)

결과적으로 최소군집거리 30m의 Buffer 반경 분석은 기존 HS_KDE 문제점인 인접도로 보행교통사고로 인한 확률밀도 증가로 HS이 선정되는 오류 등 기존 다발지점 선정 한계를 일정 부문 보완해 줄 수 있다. 또한, 보행교통사고 HS에 대한 최소거리 적용은 앞선 Figure 3과 같이 모든 방향에서 우회전 사고가 발생하는 Ped-HS 보다는 특정방향으로 우회전사고가 많이 발생하는 더 위험한 Ped-HS이 선정될 가능성이 높아진다. 마지막으로 주행속도에 따른 차량의 이동거리보다 매우 작은 보행자 이동거리를 반영한 세밀한(Micro) Ped-HS 선정 등의 장점이 있다.

공간적 특성 분석(Spatial Characteristics)

앞서 선정된 Buffer 반경 30m 이내의 Ped-HS_KDE와 주변 교통환경과의 특성을 분석하기 위해 Q-GIS를 활용하여 교차로, 도로폭, 토지이용 등의 공간데이터와 공간적 위치를 기반으로 ‘내부위치’(are within), ‘최단거리’(Shortest Distance) 등의 방법으로 공간 속성을 결합하여 분석하였다.

Table 7은 서울시 열린데이터광장의 교차로 공간데이터를 기준으로 Ped-HS_KDE의 중심점 및 개별 보행교통사고의 거리를 공간분석을 통해 산출한 결과이다. 교차로 기준은 교통신호기로 신호제어가 되는 곳으로 1R은 횡단보도 등이 있는 단일로에 경보등을 포함한 교통신호기가 설치된 곳이고, 3R은 3지교차로, 4R은 4지교차로를 말한다. 무신호 도로는 교통신호기로 제어되지 않는 일반적인 단일로와 생활도로 교차지점을 포함한다. 신호기가 설치된 교차로 경계면과 교차로 부근 공간위치를 획득하기 위해 행정안전부 새주소전자지도의 도로폭 데이터를 공간 결합한 가상자료를 통해 분석하였다.

공간분석 결과 개별 보행교통사고는 무신호 도로에 50~60%가 위치하고 있다. 대다수 지점이 신호교차로로 선정되는 교통사고 잦은 곳과 달리 Ped-HS_KDE은 교차로 부근에서 30m 이상 이격된 무신호 도로 중심으로 40~50%의 Ped-HS_KDE이 선정되고, 신호기가 설치된 단일로(1R)에서 다음으로 많은 Ped-HS_KDE이 선정됨을 알 수 있다. 또한 3지교차로보다 4지교차로의 Ped-HS_KDE가 많이 나타났다.

Table 7.

Number of Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by year by road type

Years Type			Ped-HS_{KDE(Rad.=30m)}							Ped. Crashes
Years Type			2016	2017	2018	2019	2020	2021	2022		2016	2017	2018	2019	2020	2021	2022
Nearest the		Num.	1,127	1,045	1,015	963	643	588	638		5,017	4,688	4,709	4,439	3,358	3,000	3,327
Sig. Intersection		%	58.6%	58.2%	57.4%	57.2%	54.5%	53.5%	52.6%		47.0%	45.7%	47.2%	44.9%	43.8%	42.4%	42.6%
	1R		602	521	521	517	338	335	310		2,656	2,441	2,470	2,377	1,783	1,671	1,735
	3R		157	153	157	125	81	79	92		744	682	703	626	451	407	486
	4R		359	363	328	309	218	168	227		1,584	1,534	1,500	1,403	1,093	900	1,081
	5R		8	8	9	11	6	6	7		31	30	34	31	28	22	20
	6R		1	-	-	1	-	-	2		2	1	2	2	3	-	5
Unsignalized roads		Num.	796	750	754	722	536	512	575		5,666	5,561	5,269	5,457	4,313	4,075	4,480
Unsignalized roads		%	41.4%	41.8%	42.6%	42.8%	45.5%	46.5%	47.4%		53.0%	54.3%	52.8%	55.1%	56.2%	57.6%	57.4%

note : Sig. Intersection is controlled by traffic signals. Unsignalized roads are not controlled by traffic signals. 1R(One-way street), 3R(3 Right-Turn), 4R(4 Right-Turn), 5R(5 Right-Turn), 6R(6 Right-Turn)

Table 8은 도로폭 자료가 있는 행정안전부 새주소전자지도 도로망 데이터와의 공간분석을 통해 산출한 결과이다. 각 연도별 보행교통사고는 12m 미만의 소로에서 50% 이상이 발생하는 것으로 나타났고, Ped-HS_KDE도 12m 미만의 소로에서 약 50%의 수치로 선정됨을 알 수 있다. 2022년 기준 25m 이하의 소로와 중로에서 약 75%가 Ped-HS_KDE가 선정되는 것으로 나타났다.

Table 8.

Number of Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by year by road width

Years Road width		Ped-HS_{KDE(Rad.=30m)}							Ped. Crashes
Years Road width		2016	2017	2018	2019	2020	2021	2022	2016	2017	2018	2019	2020	2021	2022
< 12m	Num.	862	821	850	823	595	588	630	5,371	5,347	5,280	5,359	4,272	3,974	4,458
< 12m	%	44.8%	45.7%	48.0%	48.8%	50.5%	53.5%	51.9%	52.2%	52.9%	54.2%	55.7%	56.2%	57.1%	53.8%
12m ≦	Num.	450	448	433	412	289	256	302	2,518	2,351	2,337	2,237	1,687	1,622	1,701
12m ≦	%	23.4%	25.0%	24.5%	24.5%	24.5%	23.3%	24.9%	22.9%	23.4%	22.6%	22.0%	22.9%	21.8%	22.8%
25m ≦	Num.	460	396	363	333	219	199	218	2,040	1,901	1,721	1,686	1,210	1,092	1,252
25m ≦	%	23.9%	22.1%	20.5%	19.8%	18.6%	18.1%	18.0%	18.5%	17.2%	17.0%	15.8%	15.4%	16.0%	17.2%
40m ≦	Num.	151	130	123	117	76	57	63	754	650	640	614	502	387	396
40m ≦	%	7.9%	7.2%	7.0%	6.9%	6.4%	5.2%	5.2%	6.3%	6.4%	6.2%	6.5%	5.5%	5.1%	6.2%

Table 9는 도로폭에 따른 2022년 보행교통사고의 사고유형별 결과로, Ped-HS_KDE의 교통사고와 보행교통사고 모두 보행자의 횡단중 사고비율이 높으며, 도로폭에 따른 사고유형은 광로와 달리 소로에서는 차도통행중, 길가장자리통행중 사고 비율이 높은 것으로 나타났다.

Table 9.

Number of pedestrian crashes in Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by road width, 2022

Years Road width	Ped. Crashes in Ped-HS_{KDE(Rad.=30m)}						Ped. Crashes
Years Road width	Sub total	Crossing	Passing on road	Passing on roadside	Passing on sidewalk	Others		Sub total	Crossing	Passing on road	Passing on roadside	Passing on sidewalk	Others
< 12m	1,520	372	178	129	83	758		4,458	939	515	393	275	2,336
12m ≦	705	332	52	23	56	242		1,701	718	144	41	153	645
25m ≦	502	235	22	6	51	188		1,252	532	65	14	171	470
40m ≦	141	55	8	1	18	59		396	147	20	3	47	179

Table 10은 토지이용 자료가 있는 국토교통부의 용도지역 데이터와 공간분석을 통해 산출한 결과로 보행교통사고와 Ped-HS_KDE 모두 주거지역에서 75% 이상 발행하고 있는 것으로 나타났다.

Table 10.

Number of Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by year by zoning

Years Zoning		Ped-HS_{KDE(Rad.=30m)}							Ped. Crashes
Years Zoning		2016	2017	2018	2019	2020	2021	2022		2016	2017	2018	2019	2020	2021	2022
Residential area	Num.	1,493	1,377	1,357	1,271	911	845	909		8,335	7,817	7,746	7,593	5,913	5,508	6,062
Residential area	%	77.6%	76.7%	76.7%	75.4%	77.3%	76.8%	74.9%		78.0%	76.3%	77.6%	76.7%	77.1%	77.9%	77.6%
Commercial areas	Num.	305	312	293	293	182	177	240		1,504	1,635	1,471	1,494	1,082	915	1,177
Commercial areas	%	15.9%	17.4%	16.6%	17.4%	15.4%	16.1%	19.8%		14.1%	16.0%	14.7%	15.1%	14.1%	12.9%	15.1%
Industrial areas	Num.	74	67	77	82	58	52	43		446	387	432	464	360	343	282
Industrial areas	%	3.8%	3.7%	4.4%	4.9%	4.9%	4.7%	3.5%		4.2%	3.8%	4.3%	4.7%	4.7%	4.8%	3.6%
Green areas	Num.	43	31	29	32	26	22	15		347	369	284	310	295	284	245
Green areas	%	2.2%	1.7%	1.6%	1.9%	2.2%	2.0%	1.2%		3.2%	3.6%	2.8%	3.1%	3.8%	4.0%	3.1%
ETC	Num.	8	8	13	7	2	4	6		51	41	45	35	21	25	41
ETC	%	0.4%	0.4%	0.7%	0.4%	0.2%	0.4%	0.5%		0.5%	0.4%	0.5%	0.4%	0.3%	0.4%	0.5%

교차로, 도로폭, 토지이용 등의 공간데이터와 공간 위치를 기반으로 공간 통계분석 한 결과 단일로, 소로, 주거지역 등에서 보행교통사고 비율이 높게 나타나 주거생활권 도로에 대한 보행안전정책이 지속적으로 추진되어야 함을 시사해 주고 있다.

결론

본 연구는 보행교통사고 다발지점 선정을 위해 보행교통사고의 점 패턴 자료에 대한 공간분석을 시도하였다. 이를 위해 전체 교통사고 사망자 대비 보행사망자 비율이 높은 서울특별시를 대상으로 2016년에서 2022년까지 발생한 보행교통사고를 분석하였다.

우선, 보행교통사고 자료의 발생 패턴 간 공간적 의존도를 분석하기 위해 Ripley의 K-function과 L-function를 통해 거리별 군집정도를 분석하였다. 분석 결과, 각 연도별 보행교통사고는 개별 사고 간의 공간적 의존성을 지닌 군집화된 상태이며, 공간적 패턴의 군집화는 30.7m 이내 거리까지 L-function 값이 급격히 증가되고 그 이상의 거리에서는 증가폭이 서서히 완화되는 것으로 나타났다. 또한, 동일한 방법으로 차대차 및 차량단독 교통사고의 군집화를 분석한 결과는 35.7m로 나타나 보행교통사고의 군집 패턴보다 1.16배 큰 것으로 나타났다.

또한, KDE를 이용하여 5m~50m까지 5m 간격의 Buffer 반경에 따른 Ped-HS_KDE를 선정하고, L-fucntion에 의해 선정된 결과의 적용 가능성을 검토한 결과 Ped-HS_KDE의 총량은 Buffer 반경 30m~35m에서 10% 미만으로 완만하게 증가하고 있으며 해당 거리 이상에서 Ped-HS_KDE 총량의 증가폭은 더 완만해지지만, Buffer 반경이 커질수록 인접 도로의 사고를 포함하는 결과도 보여주고 있다.

이러한 결과는 보행교통사고 잦은 곳의 최소 공간적 군집거리를 Ripley의 K-function과 L-function에서 도출된 반경 30m를 선택할 때 의미가 있음을 보여준다. Buffer 반경 30m의 분석은 기존 HS_KDE 문제점인 인접도로 보행교통사고로 인한 확률밀도 증가로 HS이 선정되는 오류 보완 및 특정방향으로의 더 위험한 HS 선정, 순간 이동거리가 작은 보행자 교통특성을 고려한 세밀한(Micro) HS 선정 등의 장점이 있다.

선정된 30m 반경의 Ped-HS_KDE을 교차로, 도로폭, 토지이용 등 교통지표와의 공간분석한 결과는, 기존 교통사고 잦은 곳과 다르게 Ped-HS_KDE은 광로보다는 소로 또는 중로에서 많이 선정되고, 신호교차로 중심으로 선정되는 교통사고 잦은 곳과 달리 무신호 도로와 주거지역에서 Ped-HS_KDE이 가장 많이 선정됨을 알 수 있었다. 이러한 결과는 주거생활권 도로에 대한 보행안전정책이 지속적으로 추진되어야 함을 시사해 주고 있다.

본 연구에서 사용한 K-function, L-function과 KDE의 방법은 개별사고를 동일한 가중치로 분석하는 것으로 사망사고, 중상사고, 경상사고 등 개별 보행교통사고 심각도를 반영하는 것에는 한계가 있다. 단순 보행사고건수가 많은 곳 중심으로 선정된 Ped-HS_KDE을 통해서는 개선대책 수립지점의 우선 순위를 결정하는 문제나, 시설개선 비용 등 B/C를 고려한 사업의 우선 순위를 제시하는 문제에 있어 한계를 가진다. 또한, 고령사회에 대비하여 노인보행교통사고 다발지점 등 테마형 보행교통사고 잦은 곳 선정의 적정 기준에 대한 연구도 필요하다.

향후 개별 보행교통사고 심각도를 고려하여 사고별 가중치를 반영한 Ped-HS_KDE 우선순위 선정기준을 마련할 필요가 있으며, Ped-HS_KDE의 공간적 인접 지역에 인구구조, 주변 토지이용 현황, 도로시설물 등의 세밀한(Micro) 자료와의 공간분석이 추가적으로 연구되어야 할 것이다.

References

AASHTO (2010), Highway Safety Manual, 1st Edition, American Association Of State Highway and Transportation Officials, USA.

Australian BTE (1995), Evaluation of The Black Spot Program, Bureau of Transport And Communications Economics, Australian Government Publishing Service, Canbera, Australian.

Australian Gov. DITRDCA(Dep. Infrastruct. Transp. Reg. Dev. Commun. Arts) Homepage - Local Initiatives - Black Spot Program - Site Eligibility, https://investment.infrastructure.gov.au, 2022.12.12.

Aziz S., Ram S. (2022), A Meta-analysis of the Methodologies Practiced Worldwide for the Identification of Road Accident Black Spots, Transp. Res. Procedia, 62, 790-797.

10.1016/j.trpro.2022.02.098

Baranyai D., Sipos T. (2022), Black-Spot Analysis in Hungary Based on Kernel Density Estimation, Sustain., 14, 8335.

10.3390/su14148335

Borsos A., Cafiso S., D'Agostino C., Miletics D. (2016), Comparison of Italian and Hungarian Black Spot Ranking, Transp. Res. Procedia, 14, 2148-2157.

10.1016/j.trpro.2016.05.230

Chang I. J., Park H. T., Hong E. G., Lee J. D., Kwon N. J. (2022), Predicting Effects of Built Environment on Fatal Pedestrian Accidents at Location-Specific Level: Application of XGBoost and SHAP, Accid. Anal. Prev., 166, 106545.

10.1016/j.aap.2021.10654534995959

Cheng W., Washington S. P. (2005), Experimental Evaluation of Hotspot Identification Methods, Accid. Anal. Prev., 37, 870-881.

10.1016/j.aap.2005.04.01515963449

Cui H., Dong J., Zhu M., Li X., Wang Q. (2021), Identifying Accident Black Spots Based on the Accident Spacing Distribution, J. Traffic Transp. Eng.

10.1016/j.jtte.2021.02.006

Debrabant B., Halekoh U., Bonat W. H., Hansen D. L., Hjelmborg J., Lauritsen J. (2018), Identifying Traffic Accident Black Spots with Poisson-Tweedie Models, Accid. Anal. Prev., 111, 147-154.

10.1016/j.aap.2017.11.02129202323

Dereli M. A., Erdogan S. (2017), A New Model for Determining the Traffic Accident Black Spots using GIS-aided Spatial Statistical Methods, Transp. Res. Part A, 103, 106-117.

10.1016/j.tra.2017.05.031

Elvik R. (2007), State-of-the-art Approaches to Road Accident Black Spot Management and Safety Analysis of Road Networks, The Institute of Transport Economics(TOI), Oslo, Norway.

Elyasi M. R., Saffarzade M., Boroujerdian A. M. (2016), A Novel Dynamic Segmentation Model for Identification and Prioritization of Black Spots Based on the Pattern of Potential for Safety Improvement, Transp. Res. Part A, 91, 346-357.

10.1016/j.tra.2016.06.020

Fan Z., Liu C., Cai D., Yue S. (2019), Research on Black Spot Identification of Safety in Urban Traffic Accidents Based on Machine Learning Method, Saf. Sci., 118, 607-616.

10.1016/j.ssci.2019.05.039

Flahaut B., Mouchart M., Martin E. S., Thomasa I. (2003), The Local Spatial Autocorrelation and the Kernel Method for Identifying Black Zones A Comparative Approach, Accid. Anal. Prev., 35, 991-1004.

10.1016/S0001-4575(02)00107-012971934

Ghadi M., Torok A. (2017), Comparison Different Black Spot Identification Methods, Transp. Res. Procedia, 27, 1105-1112.

10.1016/j.trpro.2017.12.104

Ghadi M., Torok A. (2019), A Comparative Analysis of Black Spot Identification Methods and Road, Accid. Anal. Prev., 128, 1-7.

10.1016/j.aap.2019.03.00230953947

Gregoriades A., Mouskos K. C. (2013), Black Spots Identification through a Bayesian Networks Quantification of Accident Risk Index, Transp. Res. Part C, 28, 28-43.

10.1016/j.trc.2012.12.008

Hong K. M., Im I. J., Kim J. H., Song J. I. (2021), Research on Selection of Vulnerable Areas to Walking Traffic Accidents for the Elderly Considering Jaywalking Accidents, J. Korean Soc. Disaster Inf., 17(2), 341-350.

Korea MOIS (2013), Guidelines of Designation and Promotion on Pedestrian Environment Improvement District, Ministry of the Interior and Safety, Sejong, South Korea.

Korea MOIS(Minist. Inter. Saf.) (2022a), Homepage - Business Information - Dangerous Road Structure Improvement Project, https://mois.go.kr, 2022.12.12.

Korea MOIS(Minist. Inter. Saf.) (2022b), Homepage - Press Release, https://mois.go.kr, 2022.12.12.

KoROAD (2021), Seoul Improvement Project at Black Spot, Korea Road Traffic Authority Seoul Branch, Seoul, South Korea.

KoROAD (2023), A Comparison of Traffic Accidents in Member States of OECD, Korea Road Traffic Authority, Wonju, South Korea.

KoROAD Homepage - Business Information - Black Spot Improvement Program, http://www.koroad.co.kr, 2022.12.05.

KoROAD TAAS(Traffic Accident Analysis System) Homepage, http://taas.koroad.co.kr, 2022.12.05.

Lee J. W., Chung K. H., Papakonstantinou I., Kang S.M., Kim D. K. (2020), An Optimal Network Screening Method of Hotspot Identification for Highway Crashes with Dynamic Site Length, Accid. Anal. Prev., 135, 105358.

10.1016/j.aap.2019.10535831765928

Lee K. Y., Chang M. S. (2005), Selecting Technique of Accident Sections using K-mean Method, Int. J. Highw. Eng., 7(4), 211-219.

Lee S. I., Yu J. S. (2010), An Analysis of the Hazardous Highway Segments using Continuous Risk Profile Method, J. Korean Soc. Safety, 25(6), 180-185.

Medury A., Grembek O. (2016), Dynamic Programming-based Hot Spot Identification Approach for Pedestrian Crashes, Accid. Anal. Prev., 93, 198-206.

10.1016/j.aap.2016.04.03727209154

Murat Y. S., Cakici Z. (2017), An Integration of Different Computing Approaches in Traffic Safety Analysis, Transp. Res. Procedia, 22, 265-274.

10.1016/j.trpro.2017.03.033

Nam K. W., Kang I. J. (2007), Verifying the Voluntariness of the Location of Drunk Driving Accidents, J. Korean Assoc. Geogr. Inf. Stud., 10(2), 129-138.

Ripley B. (1976), The Second-order Analysis of Stationary Point processes, J. Appl. Probab., 13(2), 255-266.

10.2307/3212829

Song E. G., Seo H. J., Kim K. M., Woo D. G., Park T. J., Choi T. Y. (2019), Analysis of Roadkill Hotspot According to the Spatial Clustering Methods, J. Environ. Impact Assess., 28(6), 580-591.

Washington S., Haqueb Md. M., Oh J. T., Lee D. M. (2014), Applying Quantile Regression for Modeling Equivalent Property Damage Only Crashes to Identify Accident Black Spots, Accid. Anal. Prev., 66, 136-146.

10.1016/j.aap.2014.01.00724531115

Yamada I., Thill JC. (2004), Comparison of Planar and Network K-functions in Traffic Accident Analysis, J. Transp. Geogr., 12, 149-158.

10.1016/j.jtrangeo.2003.10.006

Yang B. Z., Loo B. P. Y. (2016), Land Use and Traffic Collisions: A Link-attribute Analysis using Empirical Bayes Method, Accid. Anal. Prev., 95, 236-249.

10.1016/j.aap.2016.07.00227454868

Yang J. H., Kim J. O., Yun K. H. (2016), A Selection of High Pedestrian Accident Zones using Traffic Accident Data and GIS: A Case Study of Seoul, J. Korean Soc. Surv. Geod. Photogramm. Cartogr., 34(3), 221-230.

10.7848/ksgpc.2016.34.3.221

Journal of Korean Society of Transportation ISSN:1229-1366(Print) 2234-4217(Online) 대한교통학회지

Preview

Determining the Spatial Ranges and Characteristics of Pedestrian Hot Spots in Seoul Using L-function and KDE

ABSTRACT

MAIN

Table 1.

Road crashes: fatalities or pedestrian fatalities by country (Unit: Persons, %)

Table 2.

Road crashes: fatalities or pedestrian fatalities by region (Unit: Persons, %)

Figure 1.

Research flow

Figure 2.

The concept of the screening method (Sliding Window, SLW)

Table 3.

Summary of studies

Figure 3.

Hot spot identification (HSID) error

Figure 4.

Sample heatmap (KDE) of Gangnam station by bandwidth

Table 4.

Shortest distance between pedestrian crash positions: all pedestrian crashes vs pedestrian crashes within 100m (Unit: Numbers, m)

(1)

(2)

Figure 5.

Pedestrian crash point pattern analysis by Ripley’s K-function and L-function in Seoul, 2022

Figure 6.

L-function plot between pedestrian crashes and non-pedestrian crashes

Figure 7.

Curve of change in slope and curve of smoothed gradient change rate, L-function plot 2022

Table 5.

The distance at which the smoothed rate of change in the gradient of L(D) for Ped. Crashes and Non-Ped. Crashes

(3)

(4)

Figure 8.

Convert heatmap (KDE) data to buffered polygon data

Figure 9.

Gangnam station Ped-HSKDE sample by buffer radius, 2022

(5)

Table 6.

Ped-HSKDE containing 2 or more pedestrian crashes by year by buffer radius

Figure 10.

Gangnam station KDE and Ped-HSKDE (Buffer radius:30), errors of Ped-HSKDE (Buffer radius:50)

Table 7.

Number of Ped-HSKDE(Rad.=30m) and pedestrian crashes by year by road type

Table 8.

Number of Ped-HSKDE(Rad.=30m) and pedestrian crashes by year by road width

Table 9.

Number of pedestrian crashes in Ped-HSKDE(Rad.=30m) and pedestrian crashes by road width, 2022

Table 10.

Number of Ped-HSKDE(Rad.=30m) and pedestrian crashes by year by zoning

References

Gangnam station Ped-HS_KDE sample by buffer radius, 2022

Ped-HS_KDE containing 2 or more pedestrian crashes by year by buffer radius

Gangnam station KDE and Ped-HS_KDE (Buffer radius:30), errors of Ped-HS_KDE (Buffer radius:50)

Number of Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by year by road type

Number of Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by year by road width

Number of pedestrian crashes in Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by road width, 2022

Number of Ped-HS_{KDE(Rad.=30m)} and pedestrian crashes by year by zoning