Modeling Pedestrian Movement Behavior Using Social Force Model and Fuzzy Inference

Myungjoo Han; Dongjae Jung; Young-Ihn Lee; Soongbong Lee

doi:10.7470/jkst.2022.40.2.218

Preview

Article

Journal of Korean Society of Transportation. 30 April 2022. 218-229
https://doi.org/10.7470/jkst.2022.40.2.218

Modeling Pedestrian Movement Behavior Using Social Force Model and Fuzzy Inference

퍼지추론을 반영한 Social Force Model 기반의 보행자 이동행태 모형 개발

Myungjoo HAN¹

Dongjae JUNG²^*

Young-Ihn LEE³

Soongbong LEE⁴

한 명주¹

정 동재²^*

이 영인³

이 숭봉⁴

¹Research Fellow, Gyeonggi Public Investment Management Center, Gyeonggi Research Institute, Gunpo 15880, Korea

²Research Fellow, Department of Transportation and Logistics Research, Incheon Research Institute, Incheon 22711, Korea

³Professor, Graduate School of Environmental Studies, Seoul National University, Seoul 08826, Korea

⁴Research Fellow, Division for AI and Big Data Platform, The Korea Transport Institute, Sejong 30147, Korea

¹경기연구원 공공투자관리센터 투자분석위원

²인천연구원 교통물류연구부 부연구위원

³서울대학교 환경대학원 명예교수

⁴한국교통연구원 AI ‧ 빅데이터플랫폼연구팀 부연구위원

^{*Corresponding Author}

ABSTRACT

The aim of this paper is to develop a microscopic pedestrian movement behavior model reflecting the walking speed and direction of pedestrians through fuzzy inference approach and social force model. The model can analyze the movement of each pedestrian and the interaction between pedestrians by using individual pedestrians as the unit of analysis, which would complement the limitations of existing studies have analyzed pedestrians as homogeneous and continuous flow. In addition, by reflecting the pedestrian’s probabilistic decision-making process on the change of walking speed and direction, the limited assumption of the social force model that assumes the pedestrian’s movement is deterministic has been alleviated in this model. In the process, fuzzy inference approach was applied to process pedestrians’ subjective and ambiguous information about the pedestrian’s decision-making factors. The model was verified by comparing simulated model values and actual observations using object-oriented programming for each macroscopic and microscopic characteristics. The results of verification would show the error in the explanatory power of the model was low, and the explanatory power of the model was high.

Keywords

decision-making process

fuzzy inference

pedestrian movement behavior

pedestrian simulation

social force model

이 연구는 퍼지추론을 적용한 보행속력 또는 이동방향 변경확률 모형을 사회역학모형 기반의 반응행태 모형에 반영한 미시적 보행자 이동행태 모형을 개발하였다. 이 모형은 개별 보행자를 분석 단위로 하여 보행자 특성별 움직임과 보행자간 상호작용을 분석할 수 있다는 점에서 보행자 집단을 동질적이고 연속된 흐름으로 간주하고 집계된 평균 특성으로 보행행태를 분석하는 거시적 접근법 연구의 한계를 보완한다. 또한 보행속력 또는 이동방향 변경에 대한 보행자의 확률적 의사결정 행태를 반영함으로써 보행자의 움직임을 결정적이라 전제하는 사회역학모형의 이론적 가정을 완화하였다. 이 과정에서 보행자의 의사결정 요인에 관한 보행자의 주관적이고 애매한 정보를 처리하기 위하여 퍼지추론이 적용되었다. 모형의 검증은 객체지향 프로그래밍을 활용하여 시뮬레이션한 모형치와 실제 관측치를 비교하며 이루어졌다. 두 가지 관점의 보행특성, 즉 거시적 보행특성과 미시적 보행특성에 대한 설명력을 검토하였는데, 모두 오차가 크지 않고 관측치에 대한 모형치의 설명력이 높게 도출되었다.

키워드

의사결정과정

퍼지추론

보행이동행태

보행시뮬레이션

사회역학모형

MAIN

서론
선행연구 고찰
연구 방법론
1. 퍼지추론을 활용한 의사결정 모형
2. 사회역학모형 기반의 확률적 반응행태 모형
퍼지추론 적용 및 결과
모형 검증
결론

서론

최근 보행교통과 그 공간의 중요성에 대한 공감이 높아지고 있다. 보행자의 이동행태를 정밀하게 모사할 수 있는 보행행태 모형은 보행공간의 계획과 관리, 그리고 관련 정책사업 평가에서 활용도가 높을 것이다. 보행행태 모형은 보행자의 의사결정 과정에 따라 크게 세 단계, 즉 전략단계(strategic level), 전술단계(tactical level), 실행단계(operational level)모형으로 구분되는데(Hoogendoorn et al., 2002), 이 연구의 논의 대상인 실행단계 모형은 전략단계, 전술단계 모형에 비해 상대적으로 연구가 부족하다. 또한 실행단계 모형에 관한 대부분의 연구는 보행자 집단을 동질적이고 연속된 흐름으로 간주하고 집계된 평균 특성으로 보행행태를 분석하는 거시적 접근법(macroscopic approaches) 연구로 분류된다. 거시적 관점의 연구는 적용이 쉬워 광범위하게 사용되고 있으나, 보행자간 또는 보행자와 장애물간 상호작용을 고려하기에는 한계가 있다.

이 연구는 보행자의 실행단계에 대한 미시적 보행자 이동행태 모형을 개발하고자 한다. 여기서 ‘미시적’이라 함은 앞서 거시적 접근법과 대비되는, 개별 보행자를 분석 단위로 하는 것을 의미한다. 보행자들을 하나의 동질적 집단이 아닌 자율성(autonomy)을 가진 개별 지적 행위자(intelligent agent)로 전제하여 보행자 특성별 움직임과 보행자 간 상호작용을 고려할 수 있다. 한편 각 보행자가 이동방향과 속력을 변경하는 행태를 구현하기 위해서는 의사결정에 영향을 끼치는 요인에 대한 보행자의 주관적이고 애매(fuzzy)한 정보를 처리하는 과정이 요구된다. 또한 이 의사결정이 실제 이동행태로 드러나고 다시 다른 보행자와 상호작용하는 이동행태가 구현될 수 있어야 한다. 이 연구는 퍼지추론법(Fuzzy Inference)을 적용하여 보행자가 이동방향 또는 속력을 수정하는 의사결정 확률 모형을 개발하고, 이 의사결정 확률을 보행자 반응행태 모형 중에서 대표적인 사회역학모형에 반영하여 시뮬레이션 및 검증을 수행하고자 한다.

이 연구는 먼저 2장 선행연구 고찰을 통해서 보행행태 모형의 범위와 이 연구의 대상을 설정한다. 또한 미시적 보행행태 모형의 필요성과 함께 해당 모형의 개선을 위한 확률적 의사결정 개념과 퍼지추론의 필요성을 제시한다. 3장은 이 연구의 보행자 이동행태 모형을 구성하는 두 하부 모형, 즉 보행자가 이동 방향 또는 속력을 변경할 것인지 여부를 정하는 확률적 의사결정 모형과 이 의사결정을 실제 행동으로 옮기는 반응행태 모형에 관해 설명한다. 의사결정 모형은 퍼지추론법을 활용하고, 반응행태 모형은 사회역학모형에 의사결정 확률을 반영하여 보행자 간 상호작용 및 이동행태를 분석한다. 이어서 4장은 퍼지추론 적용 및 결과를 제시하고, 5장에서는 모형을 시뮬레이션하고 검증 결과를 제시한다. 마지막 6장은 연구내용을 요약하고 연구의 의의와 향후 연구과제를 정리한다.

선행연구 고찰

보행자의 행태를 체계적으로 분석하기 위하여 보행행태 연구는 보행자의 의사결정 과정을 기준으로 크게 세 단계로 구분한다(Hoogendoorn et al., 2002). 첫 번째 단계는 출발시간 또는 보행공간 내 목적지를 선택하는 단계(전략 단계, strategic level), 두 번째 단계는 활동스케쥴 및 경로를 결정하는 단계(전술 단계, tactical level), 세 번째 단계는 이동을 하면서 다른 보행자 또는 장애물과 상호작용하는 단계(실행 단계, operational level)이다. 이 연구가 초점을 두는 실행단계에서의 보행자 이동행태는 거시적 접근법(macroscopic approaches)과 미시적 접근법(microscopic approaches)으로 분석할 수 있다. 거시적 접근법은 보행자들을 동질적이고 연속된 흐름(flow)으로 가정하고 보행량-밀도-속도 관계식에 기반을 둔 분석 방법이다(Fruin, 1971). 거시적 접근법은 적용이 간단하고 쉽지만 보행자 및 장애물 간 상호작용을 고려하지 못한다. 따라서 보행공간의 운영기법에 따른 서비스수준 차이를 설명하지 못하는 한계가 있다(Helbing and Molnar, 1998).

반면 미시적 접근법은 개별 보행자 단위의 움직임과 상호작용을 분석한다(Helbing and Molnar, 1995; Werner and Helbing, 2003; Seyfried et al., 2006). 초기에는 보행자의 이동과 상호작용을 기체 및 유체의 입자(Henderson, 1974; Helbing, 1992) 또는 자기력(Okazaki, 1979)에 비유해 설명하는 방식이 제안되었다. 이후 개발된 사회역학모형(Social Force Model; Helbing and Molnar, 1995)은 세 종류의 힘, 즉, 목적지를 향해 속도를 유지하려는 힘(driving force), 다른 보행자나 장애물과 적정 거리를 유지하려는 척력(repulsive force), 동반자나 상점 등 매력 요인에 더 가까이 가려는 인력(attractive force)의 합을 의미하는 사회역학(social force)으로 보행자의 움직임과 상호작용을 설명한다. 사회역학모형은 Vissim과 같은 상용 시뮬레이터에 적용되는 등 보행자의 이동과 상호작용을 구현하는 대표적인 모형으로 자리 잡았다.

다만 사회역학모형은 보행자의 움직임을 결정적(deterministic)이라 가정한다. 보행자의 이동행태는 보행자의 특성, 행동 규칙, 보행환경 등과 같은 다양한 요인에 따라 확률적이라 가정하는 것이 이론적으로 합리적이다. 사회역학모형에 보행자의 확률적 이동행태를 반영하기 위한 논의가 추가로 필요한 이유이다. 한편, 보행자의 확률적 이동 행태를 분석하기 위해서는 보행자들의 의사결정 및 반응 행태 요인에 관한 보행자들의 주관적이고 애매(fuzzy)한 정보를 처리하는 과정이 선행되어야 한다. 그 방법으로 퍼지추론이 적합한 것으로 알려져 있다. 퍼지추론은 Zadeh(1975)이 제안한 이론으로서, 명확하지 않은 값을 정량화하여 수학적으로 다루고자 할 때 유용한 방법론이다. 특히 인간의 언어와 사고에 관련된 부정확성과 애매함을 수리적으로 처리할 수 있는 강점이 있다(Zadeh, 1975; Ross, 1995; Tsoukalas and Uhrig, 1997; Mathworks, 2014; Peeta and Zhou, 2004). 교통분야에서는 Pappis and Mamdani(1977)가 독립교차로의 신호제어전략 수립에 퍼지추론을 적용한 이래로 경로선택 영향요인 분석(Teodorovic and Kikuchi, 1991; Lotan and Koutsopoulos, 1993), 교통사고 예측모형(Kim et al., 2006), 차량추종 및 차로변경 행태에 영향을 미치는 주관적이고 애매한 요인의 정량화(Peeta and Zhou, 2004; Park et al., 2008), 보행자의 보행공간 및 환경을 인지하는 행태(Golledge et al., 1993; Gerdelan and O'Sullivan, 2010; Nasir et al., 2014) 등 다양한 부문에서 활용된 바 있다.

연구 방법론

이 연구에서 제시하는 보행자 이동행태 모형은 두 단계의 하부 모형 즉, 보행자가 이동 방향 또는 속력을 변경할 것인지 여부를 정하는 확률적 의사결정 모형과 이 의사결정을 실제 행동으로 옮기는 반응행태 모형으로 구성된다. 의사결정 모형은 퍼지추론법을 활용하여 보행자의 특성, 보행공간의 속성, 다른 보행자 및 장애물과 상호작용 등이 보행자의 의사결정 과정에 미치는 영향을 추정하고, 이동방향 또는 속력을 수정할 확률을 산출한다. 반응행태 모형은 사회역학모형에 퍼지추론으로 도출된 의사결정 확률을 반영하여 보행자 이동과 보행자 간, 또는 장애물과 상호작용을 분석한다.

1. 퍼지추론을 활용한 의사결정 모형

이 연구는 보행자가 이동방향 또는 속력을 수정하는 의사결정 확률 $A$ 를 Equation 1과 같이 퍼지추론 모형 $g (∙)$ 으로 수리화한다. 또한 그 확률은 보행자의 특성 요인, 보행공간의 물리적 환경 요인, 다른 보행자 및 장애물과의 상호작용 요인에 영향을 받는 것으로 설정한다.

(1)

A_{k, t} = g (Ω (X_{k}), Ω (Y_{k}), Ω (Z_{k})) = \sum_{l = 1}^{L} Ω_{l} Ω_{l} (X_{k}^{l}) + \sum_{m = 1}^{M} Ω_{m} Ω_{m} (Y_{k}^{m}) + \sum_{n = 1}^{N} Ω_{n} Ω_{n} (Z_{k}^{n})

여기서, $A_{k, t}$ 는 보행자 $k$ 가 시점 $t$ 에서 이동 방향 또는 속력을 변경할 확률, $X_{k}^{l}$ 는 보행자 $k$ 의 특성 $l$ , $Y_{k}^{m}$ 는 보행자 $k$ 가 보행하고 있는 공간의 물리적 환경 요인 $m$ , $Z_{k}^{n}$ 는 보행자 $k$ 의 다른 보행자 및 장애물과의 상호작용 요인 $n$ 을 의미한다. 또한, $Y_{k}$ 와 $Z_{k}$ 는 보행자의 현재위치 ${\vec{x}}_{k, t}$ 에 의해 결정된다. 세 영향 요인 $X_{k}^{l}$ , $Y_{k}^{m}$ , $Z_{k}^{n}$ 이 내포한 주관성과 애매함은 퍼지연산 및 비퍼지화 과정 $Ω (∙)$ 과 가중치 $ω$ 로 가중합산하는 과정을 통해 처리된다.

$A_{k, t}$ 의 퍼지추론 모형 $g (∙)$ 는 크게 5단계 즉, IF-THEN 규칙 생성, 소속도 함수 구축, 퍼지연산, 비퍼지화, 가중치 적용 과정을 거치며 추정된다. 첫 번째 IF-THEN 규칙 생성 단계에서는 독립변수 역할을 하는 조건부와 종속변수 역할을 하는 결론부간의 관계를 설정한다. 즉, 조건부는 영향요인 $X_{k}^{l}$ , $Y_{k}^{m}$ , $Z_{k}^{n}$ 별 상태 수준이며, 결론부는 조건부에 대해 보행자가 이동 방향 또는 속력을 변경할 확률 $A_{k, t}$ 의 수준으로 구성된다. 일반적으로 IF-THEN 규칙은 직관적 추론을 근거로 생성하지만 이 연구에서는 Han et al.(2018)의 연구 결과를 참고하여 보행자 특성 요인 $X_{k}^{l}$ 에는 연령, 성별, 보행목적을, 보행공간의 물리적 환경 요인 $Y_{k}^{m}$ 에는 보행공간의 폭을, 상호작용 요인 $Z_{k}^{n}$ 에는 다른 보행자 및 장애물과의 거리, 장애물이 위치한 각도, 상대속도를 포함한다. 조건부 및 결론부 변수의 수준은 상, 중, 하 등 복수의 주관적 등급으로 구분할 수 있는데, 이 연구에서는 성별처럼 구분이 명확한 변수의 경우 그 구분을 따르고, 이외의 변수는 3개의 수준으로 구분한다.

두 번째 단계에서는 성별 등 경계가 명확한 변수를 제외한 모든 변수에 대해 소속도 함수를 구축한다. 소속도 함수는 IF-THEN 규칙의 조건부 및 결론부에 포함된 각 변수에 대하여 보행자 $k$ 의 값이 해당 변수의 어느 수준에 속하는지를 0과 1사이의 확률로 산출하는 함수로서, 언어 정보를 수학적으로 구현하여 정량화한다. 예컨대 소속도 함수는 다른 보행자 및 장애물과의 거리 변수의 관측값이 이 변수의 세 수준 즉, ‘가깝다’, ‘보통이다’, ‘멀다’에 각각 얼마의 확률로 소속되는지를 산출한다. 소속도 함수는 일반적으로 휴리스틱 또는 주관적 기준으로 설정하는 경우가 많은데, 이 연구에서는 장애물과의 거리, 장애물이 위치한 각도와 같은 변수는 보행 영상 자료 분석을 토대로 소속도 함수를 설정하고, 이 외의 변수는 다른 연구들에서처럼 휴리스틱 또는 사회적 합의(예컨대 나이가 많음은 60세를 기준으로 설정)를 참고해 설정한다.

세 번째로 퍼지연산 단계는 IF-THEN 규칙의 조건부와 결론부 관계를 규명한다. 퍼지연산은 일반적으로 두 퍼지집합에 대한 합집합 연산의 경우 큰 값을 취하는 ‘max연산’(최대), 교집합 연산일 경우 작은 값을 취하는 ‘min연산’(최소)이 주로 사용된다. 또한 이 외에도 ‘product연산’(곱) 등 다양한 종류가 활용된다. 대표적인 추론연산방식으로는 Mamdani 방식과 Larsen 방식이 있는데, Mamdani 방식은 max-min 방식이라고도 하며, 가장 흔히 이용되고 있다. Mamdani 방식은 퍼지 함축(implication)시 min연산을 사용하고 합성(composition)시 max-min연산을 사용한다. 반면, Larsen 방식은 퍼지 함축시 product연산를 이용하고 합성시 max-product연산을 이용한다.

네 번째, 비퍼지화는 퍼지추론에서 얻어진 퍼지 결과값을 애매성이 존재하지 않는 비퍼지값(crisp value)으로 변환한다. 추론된 출력 퍼지값들에 대응되는 수치들 중에서 가장 적당한 값을 선택하는 과정으로, 일반적으로 널리 이용되는 비퍼지화 방법은 무게중심법(centroid of area method), 최대값평균법(mean of maximum method) 등이 있다. 마지막 다섯 번째 단계에서는 각 요인의 비퍼지값에 가중치를 적용하고 합산한다. 즉, 이동방향 또는 속력 확률을 여러 요인의 중요도(가중치)를 고려하여 산출한다.

2. 사회역학모형 기반의 확률적 반응행태 모형

이 연구에서 반응행태 모형은 사회역학모형(Helbing and Molnar, 1995)을 기반으로 하되, 앞서 살펴본 퍼지추론을 활용한 의사결정 모형을 접목하여 확률개념을 도입한다. 즉, 시점 $t$ 에서 보행자 $k$ 의 이동가속도 $S F_{k, t}^{*}$ 는 Equation 2와 같이 사회역학 $S F_{k, t}$ 와 의사결정 모형으로 도출되는 보행자의 이동방향 또는 속력 수정확률 $A_{k, t}$ 로 결정된다.

(2)

S F_{k, t}^{*} = A_{k, t} \cdot S F_{k, t}

여기서, 사회역학 $S F_{k, t}$ 는 보행자와 주변의 다른 보행자, 또는 물리적, 환경적 요인들간 상호작용으로 인해 보행자의 속도에 영향을 미치는 힘을 정의한 개념으로서, Equation 3과 같이 보행자가 목적지로 향하며 속도를 유지하려는 힘 ${\vec{f}}_{k}^{o}$ , 다른 보행자나 물체 $β$ 들로부터 멀어지려는 힘 $\sum_{β} {\vec{f}}_{k β}$ , 동반자, 상점 등의 매력 요인 $A T T$ 로 향하려는 힘 $\sum_{γ} {\vec{f}}_{k γ}^{A T T}$ 의 합으로 표현된다.

(3)

S F_{k, t} = {\vec{f}}_{k}^{o} + \sum_{β} {\vec{f}}_{k β} + \sum_{γ} {\vec{f}}_{k γ}^{A T T}

퍼지추론 적용 및 결과

보행자가 이동방향 또는 속력을 수정하는 확률 $A$ 에 관한 퍼지추론 결과는 다음과 같다. 우선 IF-THEN 규칙은 Table 1과 같이 설정하였다. IF-THEN 규칙의 조건부는 보행자 특성 요인 $X_{k}^{l}$ 인 연령, 성별, 보행목적을, 보행공간의 물리적 환경 요인 $Y_{k}^{m}$ 인 보행공간의 폭을, 상호작용 요인 $Z_{k}^{n}$ 인 다른 보행자 및 장애물과의 거리, 장애물이 위치한 각도, 상대속도를 포함하였다. IF-THEN 규칙의 결론부는 보행자가 이동 방향 또는 속력을 변경할 확률 $A_{k, t}$ 을 ‘높음’, ‘보통’, ‘낮음’으로 설정하였다. 퍼지 개념이 적용되지 않는 성별과 통행목적 요인은 각각 남/녀, 업무/여가 목적의 2개 수준으로, 이외의 요인은 3개 수준으로 구분하였다.

Table 1.

IF-THEN rules for modeling pedestrian movement behavior

IF (LHS)		THEN (RHS)
Age	Young	High chance of changing walking direction or speed
	Middle	Medium chance of changing walking direction or speed
	Old	Low chance of changing walking direction or speed
Gender*	Male	High chance of changing walking direction or speed
Gender*	Female	Low chance of changing walking direction or speed
Trip purpose*	Business	High chance of changing walking direction or speed
Trip purpose*	Non-business	Low chance of changing walking direction or speed
Distance	Near	High chance of changing walking direction or speed
	Medium	Medium chance of changing walking direction or speed
	Far	Low chance of changing walking direction or speed
Angle	Front	High chance of changing walking direction or speed
	Medium	Medium chance of changing walking direction or speed
	Side	Low chance of changing walking direction or speed
Relative speed	Approach	High chance of changing walking direction or speed
	Same	Medium chance of changing walking direction or speed
	Far away	Low chance of changing walking direction or speed
Width	Narrow	High chance of changing walking direction or speed
	Medium	Medium chance of changing walking direction or speed
	Wide	Low chance of changing walking direction or speed

note: * indicates variables that belong crisp sets.

IF-THEN 규칙에 포함된 각 변수의 소속도 함수는 Table 2와 같이 설정하였다. 변수 중에서 ‘장애물과의 거리’, ‘장애물이 위치한 각도’ 변수의 소속도 함수는 보행자 영상자료를 분석한 결과를 참고해 설정하였고, 이 외에 소속도 함수 형태에 관한 별도의 자료분석이 어려운 변수는 다른 연구들에서처럼 휴리스틱 또는 사회적 합의(예컨대 나이가 많음은 60세를 기준으로 설정)를 참고하여 설정하였다. 소속도 함수의 형태는 퍼지수의 표현과 연산이 비교적 간단하여 문헌에서도 경험적으로 선호되는 삼각형 형태와 사다리꼴 형태를 적용하였다. ‘장애물과의 거리’, ‘장애물이 위치한 각도’ 변수의 소속도 함수 설정에 활용된 영상자료는 국가교통핵심기술개발사업인 ‘교통연계 및 환승시스템 기술개발’ 연구과제에서 수집된 것으로서 장애물이 있는 공간에서 보행자 이동행태를 촬영한 것이다(상세한 실험 개요는 Sung et al.(2011) 참조). 영상자료에서 보행자의 궤적 정보를 Matlab의 Motion-Based Multiple Object Tracking 기능을 활용하여 추출하고, 궤적 정보를 이용해 보행자가 다른 보행자와 장애물에 반응하여 속도가 크게 변하는 시점에서의 다른 보행자 및 장애물과의 거리, 장애물이 위치한 각도를 분석하였다. 그 결과는 회피시작 시점에서 장애물까지 거리의 평균은 3.423m, 장애물이 위치한 각도는 보행자의 진행방향을 기준으로 평균 13.331°로 도출되었다. 이 결과를 참고하여 두 변수의 소속도 함수의 파라미터를 설정하였다.

Table 2.

Membership functions

Variables		Membership functions
Variables		Category	Shape	Parameter
RHS (THEN-)	Changing walking direction or speed	Low	Triangle	[0, 0, 0.4]
		Medium	Triangle	[0.1, 0.5, 0.9]
		High	Triangle	[0.6, 1, 1]
LHS (IF-)	Age	Young	Trapezoid	[0, 0, 20, 40]
		Middle	Triangle	[30, 45, 60]
		Old	Trapezoid	[50, 70, 100, 100]
	Distance*	Near	Trapezoid	[0, 0, 1, 3.5]
		Medium	Triangle	[1, 3.5, 6]
		Far	Trapezoid	[3.5, 6, 10, 10]
	Angle*	Front	Trapezoid	[0, 0, 5, 20]
		Medium	Triangle	[5, 20, 35]
		Side	Trapezoid	[20, 35, 90, 90]
	Relative speed	Approach	Triangle	[-3, -3, 0]
		Same	Triangle	[-1, 0, 1]
		Far away	Triangle	[0, 3, 3]
	Width	Narrow	Trapezoid	[0, 0, 2, 3]
		Medium	Triangle	[2, 4, 6]
		Wide	Trapezoid	[3, 6, 10, 10]

note: * is based on observed data.

퍼지연산 단계에서는 퍼지추론에서 대표적으로 활용되는 Mamdani 형태의 추론연산을 사용하였다. 또한 비퍼지화 과정은 Mamdani 형식 추론법에서 주로 활용되는 무게중심법을 활용하였다. 퍼지연산과 비퍼지화 과정을 통해 각 변수 값의 비퍼지값(crisp value)을 도출한 후, 각 변수의 중요도를 반영하여 최종적으로 보행자별 이동방향 또는 속력 수정확률을 산출하였다. 여기서 변수의 중요도 가중치는 Table 3에 정리한 바와 같이 Han et al.(2018)에서 같은 변수에 대해 영향요인 분석을 한 결과인 표준화 계수의 적용하였다.

Table 3.

Attribute weights

Variables	Standardized coefficients	Weights
Age	-0.250	0.122
Gender	0.124	0.060
Trip purpose	0.085	0.041
Distance	0.673	0.327
Angle	0.214	0.104
Relative speed	0.570	0.277
Width	0.142	0.069

note: Han et al. (2018)

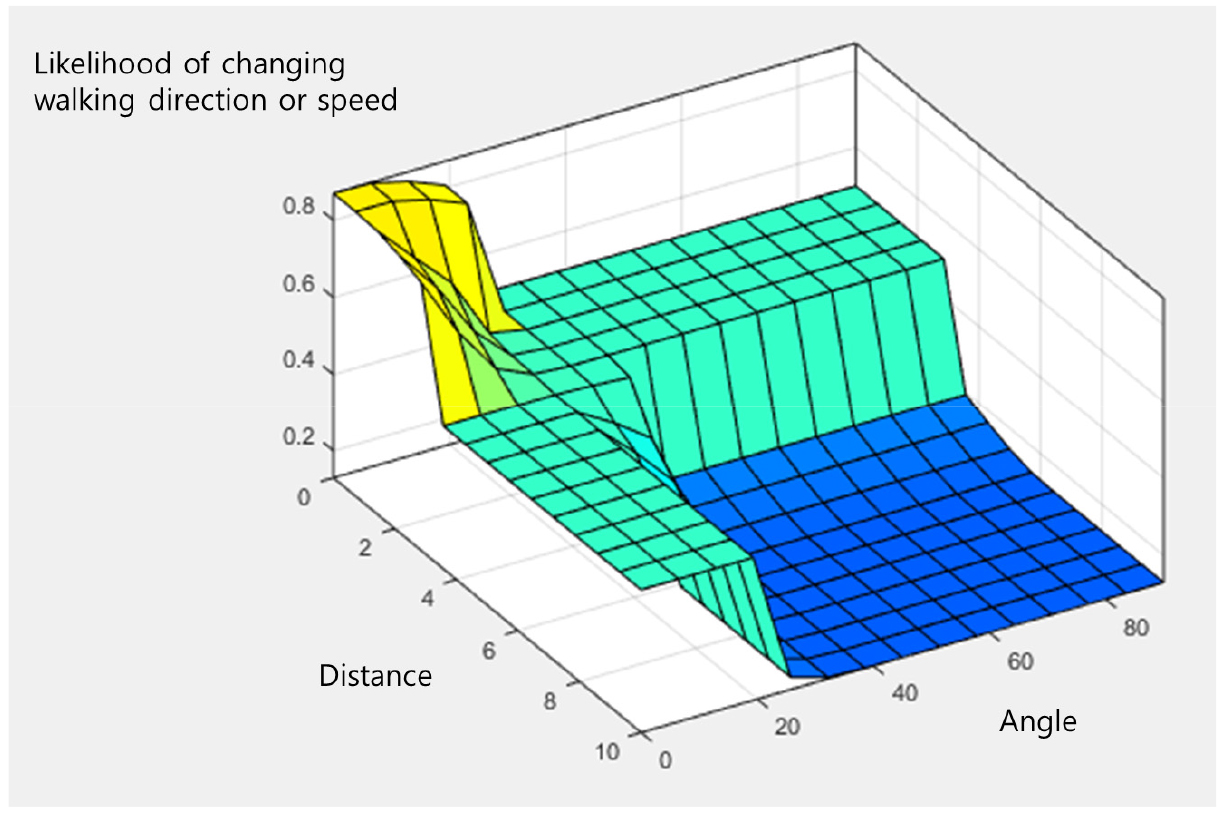
Figure 1은 다른 변수가 통제된 조건에서 장애물까지의 거리와 장애물이 위치한 각도에 따른 보행자의 이동방향 또는 속력 변경확률 $A$ 를 퍼지추론 결과를 적용하여 산출한 것이다. 또한 Table 4는 연령이 35세인 남성이 폭이 5m인 보행공간에서 업무목적의 통행을 하고 있을 때, 장애물과의 거리가 3m이며, 장애물이 정면 10°이내에서 상대속도 –2m/s로 다가오는 경우, 현재 보행 속력 및 방향을 수정할 확률이 67.5%로 산출되는 것을 보여준다.

https://static.apub.kr/journalsite/sites/kst/2022-040-02/N0210400207/images/kst_40_02_07_F1.jpg

Figure 1

The contour lines representing the likelihood of changing walking direction or speed

Table 4.

Calculating likelihood of changing walking direction or speed

Variables		Likelihood of changing walking direction or speed (A)	Weight (B)	A×B
Age	35 years	0.563	0.005	0.003
Gender	Male	0.870	0.065	0.057
Trip purpose	Business	0.870	0.055	0.048
Distance	3m	0.530	0.365	0.194
Angle	10 degree	0.647	0.125	0.081
Relative speed	-2m/s	0.858	0.308	0.264
Width	5m	0.380	0.076	0.029
Likelihood of changing walking direction or speed				0.675

모형 검증

퍼지추론을 적용한 의사결정 모형을 사회역학모형 기반의 반응행태 모형에 반영하고 객체지향 프로그래밍을 활용하여 시뮬레이션함으로써 모형을 검증하였다. 모형을 검증하기 위해 사용된 관측자료는 2012년 10월 12일에 서울시 중구 명동 엠플라자 앞 횡단거리 14m, 보도폭 9m의 보행공간을 촬영한 유동인구 영상자료에서 추출한 보행자의 궤적 정보다. 이 보행공간은 인근 지역이 중심 상업지역으로 보행량이 많고 차량통행은 제한되어 보행자간 상호작용 외의 영향은 배제할 수 있다. 분석시간은 보행량이 많은 12-13시, 16-18시, 19-20시로 선정하였다. 이 영상에서 추출된 보행자는 총775명(남자 364명, 여자 411명이고, 평균 통과시간은 14초, 평균 보행속도는 1.03m/s 수준으로 나타난다. 평균 보행속도가 기존 연구의 평균 보행속도 1.33m/s(Minister of Land, Infrastructure and Transport, 2011), 1.34m/s(Daamen, 2004)에 비해 느린 것은 분석 대상지가 중심 상업지역으로 쇼핑, 관광 등 비업무 통행목적의 보행자가 다수 포함되어 있기 때문이라 판단된다.

검증은 크게 두 가지 관점의 보행특성, 즉 거시적 보행특성과 미시적 보행특성에 대한 설명력을 검토하였다. 거시적 보행특성 검증을 위해 속도, 밀도, 보행교통류율을 5분 단위로 집계하여 48개 관측치와 모형치를 비교하였다. 미시적 보행특성 검증은 관측치와 모형치의 개별 보행자 궤적정보를 추출하여 1초 단위의 속력과 이동방향변화량 수치 600개의 분포를 비교하며 수행하였다. 한편, 보행밀도에 따른 보행특성 차이와 그 영향을 살펴보기 위하여 보행밀도가 서비스수준 A 이상의 상황과 서비스수준 B 이하의 상황을 구분하여 거시적, 미시적 보행특성을 각각 비교하였다. 여기서 서비스수준은 도로용량편람(Minister of Land, Infrastructure and Transport, 2013)을 기준으로 한다.

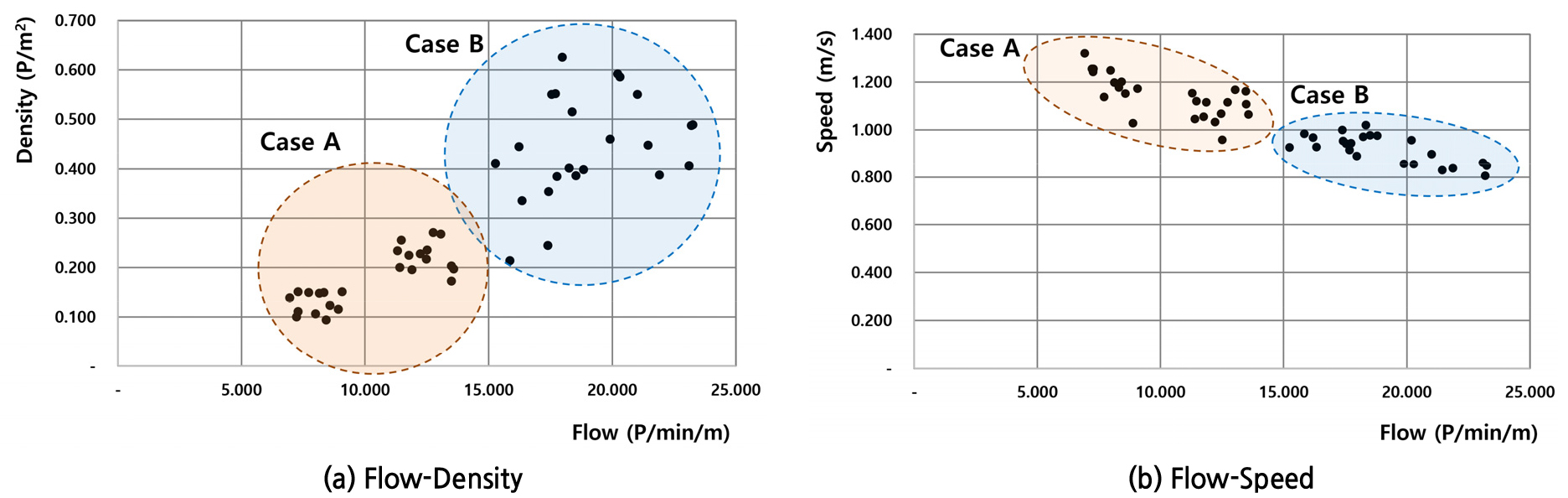
우선 검증에 사용된 관측자료의 5분 단위 집계된 개괄적인 특성을 정리하면 Figure 2, Table 5와 같다. Case A 평균 보행교통류율은 10.19인/분/m, 속력의 평균과 표준편차는 각각 1.15m/s, 0.08m/s, 평균 밀도는 0.18인/m²이다. Case B의 평균 보행교통류율은 23.25인/분/m, 속력의 평균과 표준편차는 각각 0.92m/s, 0.06m/s, 평균 밀도는 0.44인/m²이다.

https://static.apub.kr/journalsite/sites/kst/2022-040-02/N0210400207/images/kst_40_02_07_F2.jpg

Figure 2

Pedestrian traffic flow relationship (macroscopic approaches)

Table 5.

Characteristics of the macroscopic pedestrian traffic flow (observational data)

		Sample size	Min	Max	Average	s.d.
Case A	Flow (P/min/m)	24	6.93	13.58	10.19	2.38
	Density (P/m²)	24	0.10	0.27	0.18	0.06
	Speed (m/s)	24	1.03	1.32	1.15	0.08
Case B	Flow (P/min/m)	24	12.51	23.25	18.75	2.70
	Density (P/m²)	24	0.22	0.63	0.44	0.11
	Speed (m/s)	24	0.80	1.02	0.92	0.06
All	Flow (P/min/m)	48	6.93	23.25	14.47	5.01
	Sensity (P/m²)	48	0.10	0.63	0.31	0.16
	Speed (m/s)	48	0.80	1.32	1.03	0.14

note: Min, minimum; Max, maximum; s.d., standard deviation.

거시적 보행교통류 특성을 검증한 결과는 다음과 같다. 먼저 Figure 3은 전체 표본에 대해 관측치와 모형치의 속도-밀도-보행교통류율 관계를 살펴본 것이다. 관측치와 모형치가 모두 거시적 보행교통류 이론을 따르고 있다. 선형 회귀선도 이를 뒷받침한다. 특히 모형치의 속도-밀도-보행교통류율 관계 그래프에서 결정계수 $R^{2}$ 가 0.7 이상으로 도출되며 거시적 보행특성을 높은 설명력으로 구현하고 있음을 보여준다.

https://static.apub.kr/journalsite/sites/kst/2022-040-02/N0210400207/images/kst_40_02_07_F3.jpg

Figure 3

Macroscopic characteristics of pedestrian flows

관측치와 모형치의 보행교통류율-속도 관계와 보행교통류율-밀도 관계의 오차를 검증한 결과는 Table 6과 같다. 전체 표본 48개에 대한 모형치의 오차는 보행교통류율-밀도 관계의 경우 MAE 0.069, RMSE 0.100으로, 보행교통류율-속도 관계의 경우 MAE 0.059, RMSE 0.077로 나타난다. Theil의 부등계수는 보행교통류율-밀도 관계에서는 0.269, 보행교통류율-속도 관계에서는 0.136으로 나타난다. 보행교통류율-속도 관계와 보행교통류율-밀도 관계에서 모두 각 오차 평가지표의 수치가 0에 가깝게 나타나며 모형치의 설명력이 높음을 보여준다. 두 Case에 대한 오차도 0에 가깝게 나타나는 한편, 두 Case에 대한 오차를 비교하면 보행교통류율-밀도 관계의 경우 Case B에 비해 Case A의 오차가 작고, 보행교통류율-속도 관계의 경우 Case B가 Case A보다 오차가 작게 나타난다. 이는 관측자료에서 보행밀도가 높아질수록 속도의 표준편차가 작아지는 것과 무관하지 않은 것으로 판단된다.

Table 6.

Validation results

		Flow-Density	Flow-Speed
All	MAE	0.069	0.059
	RMSE	0.100	0.077
	U	0.269	0.136
Case A	MAE	0.032	0.065
	RMSE	0.047	0.089
	U	0.247	0.140
Case B	MAE	0.107	0.054
	RMSE	0.134	0.063
	U	0.272	0.129

note: MAE, mean absolute error; RMSE, root mean square error; U, Theil’s U statistic.

모형의 미시적 보행행태에 대한 설명력을 검증하기 위해서 먼저 관측 속도와 모형으로 산출된 속도의 Case별 분포를 비교하였다¹⁾. Figure 4는 Case별 관측치와 모형치의 분포를 나타낸 것이고, Table 7은 관측치와 모형치의 분포 동일성을 $χ^{2}$ 검정으로 분석한 결과다. $χ^{2}$ 검정에서 귀무가설은 ‘관측치와 모형치의 분포에 차이가 없다’로 세웠다. Case A와 Case B에서 $χ_{0}^{2}$ 가 각각 7.10, 4.82로 유의수준 0.05의 임계값 $χ^{2} (d f, 0.05)$ 인 16.92, 14.07보다 작게 나타났다. 즉, 두 Case에서 모두 귀무가설을 기각할 수 없고 관측치와 모형치의 분포가 같지 않다고 판단할 수 있는 통계적으로 유의한 차이가 발견되지 않는다.

https://static.apub.kr/journalsite/sites/kst/2022-040-02/N0210400207/images/kst_40_02_07_F4.jpg

Figure 4

Distribution of speed

Table 7.

Microscopic characteristics of pedestrian

		$d f$	$χ_{0}^{2}$	$χ^{2} (d f, 0.05)$
Distribution of speed	Case A	9	7.10	16.92
Distribution of speed	Case B	7	4.82	14.07
Distribution of walking direction	Case A	4	7.21	9.49
Distribution of walking direction	Case B	6	5.56	12.59

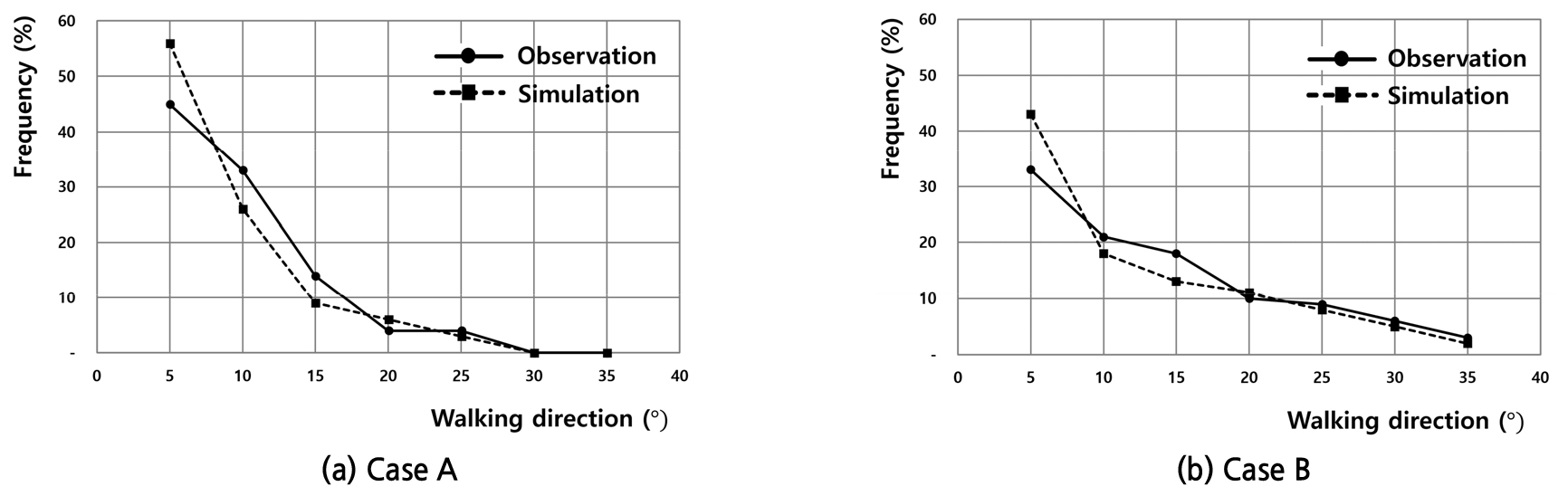
이동방향 변화량의 관측치와 모형치의 분포를 Case별로 비교²⁾하면 Figure 5와 같다. 두 Case에서 모두 관측치와 모형치의 분포가 유사하게 나타나는 한편, Case B가 Case A에 비해 관측치와 모형치 모두 크게 나타난다. 보행밀도가 용량에 도달하지 않는 수준에서 밀도가 높을수록 주변 보행자와의 상호작용이 증가해 이동방향 변경이 잦은 것으로 해석된다. 관측치와 모형치의 분포 동일성을 $χ^{2}$ 검정으로 검토한 결과는 Table 7과 같다. 귀무가설인 ‘관측치와 모형치의 분포에 차이가 없다’에 대하여 Case A와 Case B에서 $χ_{0}^{2}$ 가 각각 7.21, 5.56으로 유의수준 0.05의 임계값 $χ^{2} (d f, 0.05)$ 인 9.49, 12.59보다 작고 귀무가설을 기각하지 못한다. 즉, 관측치와 모형치의 분포가 같지 않다고 판단할 수 있는 유의한 차이가 나타나지 않는다.

https://static.apub.kr/journalsite/sites/kst/2022-040-02/N0210400207/images/kst_40_02_07_F5.jpg

Figure 5

Distribution of walking direction

결론

최근 보행교통과 그 공간의 중요성에 대한 공감이 높아지고 있다. 보행자의 이동행태를 정밀하게 모사할 수 있는 보행행태 모형은 보행공간의 계획과 관리, 그리고 관련 정책사업 평가에서 활용도가 높을 것이다. 거시적 접근법 기반의 모형은 보행공간의 용량분석에 활용도가 제한되지만, 미시적 보행자 이동행태 모형은 보행시설 설치 또는 보행정책 도입에 따른 보행공간 변화 효과와 보행자간 상호작용 효과를 분석할 수 있는 장점이 있다. 이 연구는 향후 증가할 것으로 예상되는 보행공간 평가 툴에 대한 요구에 대비하여, 미시적 보행자 이동행태 모형에 관한 논의를 진행하였다는 점에서 의의가 있다. 한편, 개별보행자 단위의 미시적 보행행태는 보행자의 특성, 주변 상황, 목적지 및 경로 특성 등 다양한 요인이 복합적으로 영향을 미칠 것으로 판단된다. 이 연구에서 다룬 요인 외에 향후 다양한 요인을 추가로 검토하여 모형의 신뢰성을 높일 수 있을 것이다. 또한 보행자 의사결정 과정에 퍼지추론을 적용하고 그 결과를 검증한 것에 연구의 의미가 있으나, 퍼지추론 각 단계에서 전제한 조건의 변화에 따른 모형 결과의 차이를 검토하지 않은 것은 연구의 한계로 남긴다.

References

Daamen W. (2004), Modelling Passenger Flows in Public Transport Facilities, Ph.D. Thesis, Delft University of Technology.

Fruin J. J. (1971), Pedestrian Planning and Design.

Gerdelan A., O'Sullivan C. (2010), A Genetic-fuzzy System for Optimizing Agent Steering, Computer Animation and Virtual Worlds, 21(3-4), 453-461. 10.1002/cav.360

Golledge R. G., Ruggles A. J., Pellegrino J. W., Gale N. D. (1993), Integrating Route Knowledge in an Unfamiliar Neighborhood: Along and Across Route Experiments, Journal of Environmental Psychology, 13(4), 293-307. 10.1016/S0272-4944(05)80252-X

Han M. J., Jung D. J., Lee Y. I., Shin S. I. (2018), Analysis of Affecting Factors to Velocity Changes of Pedestrian, J. Korean Soc. Transp., 36(5), Korean Society of Transportation, 360-370. 10.7470/jkst.2018.36.5.360

Helbing D. (1992), A Fluid-dynamic Model for the Movement of Pedestrians, Complex Systems, 6, 391-415.

Helbing D., Molnar P. (1995), Social Force Model for Pedestrian Dynamics, Physical Review E, 51(5), 4282-4286. 10.1103/PhysRevE.51.42829963139

Helbing D., Molnar P. (1998), Self-organization Phenomena in Pedestrian Crowds, Self-organization of Complex Structures: From Individual to Collective Dynamics, Gordon and Breach.

Henderson L. F. (1974), On the Fluid Mechanic of Human Crowd Motions, Transportation Research, 8, 509-515. 10.1016/0041-1647(74)90027-6

Hoogendoorn S. P., Bovy P. H. L., Daamen W. (2002), Microscopic Pedestrian Wayfinding and Dynamics Modelling, Pedestrian and Evacuation Dynamics, 123-154.

Kim J. W., Namgung M., Kim J. H., Lee S. B. (2006), Development of Traffic Accidents Prediction Model with Fuzzy and Neural Network Theory, J. Korean Soc. Transp., 24(7), Korean Society of Transportation, 81-90.

Lotan T., Koutsopoulos H. (1993), Models for Route Choice Behaviour in the Presence of Information Using Concepts from Fuzzy Set Theory and Approximate Reasoning, Transportation, 20(2), 129-155. 10.1007/BF01307056

MathWorks (2014), MATLAB Fuzzy Logic Toolbox: User's Guide.

Minister of Land, Infrastructure and Transport (2011), Technology Development of Intermodal Connectivity and Transfer Systems (The R&D Project).

Minister of Land, Infrastructure and Transport (2013), Highway Capacity Manual.

Nasir M., Lim C. P., Nahavandi S., Creighton D. (2014), A Genetic Fuzzy System to Model Pedestrian Walking Path in a Built Environment, Simulation Modelling Practice and Theory, 45, 18-34. 10.1016/j.simpat.2014.03.002

Okazaki S. (1979), A Study of Pedestrian Movement in Architectural Space, Part 1: Pedestrian Movement by the Application on of Magnetic Models, Transactions of Architectural Institute of Japan, 283, 111-119. 10.3130/aijsaxx.283.0_111

Pappis C., Mamdani E. (1977), A Fuzzy Controller for a Traffic Junction, IEEE Transactions on Systems, Man and Cybernetics, 7(10), 707-717. 10.1109/TSMC.1977.4309605

Park H. J., Bae S. H., Jung H. J. (2008), Development of Car Following Model of Adaptive Cruise Controlled Vehicle Considering Human Factors, J. Korean Soc. Transp., 26(2), Korean Society of Transportation, 121-133.

Peeta S., Zhou W. (2004), Minimizing Truck-car Conflicts on Highway, JTRP Technical Reports. 10.5703/1288284313270

Ross T. J. (1995), Fuzzy Logic with Engineering Applications, McGraw-Hill.

Seyfried A., Steffen B., Lippert T. (2006), Basics of Modelling the Pedestrian Flow, Physica A, 368(1), 232-238. 10.1016/j.physa.2005.11.052

Sung G. B., Han M. J., Lee Y. I., No M. S. (2011), Analysis of Obstacle Avoidance Behavior of Pedestrian from Field Survey Using Video Tracking Data, Journal of Transport Research, 18(2), 61-75. 10.34143/jtr.2011.18.2.61

Teodorovic D., Kikuchi S. (1991), Application of Fuzzy Sets Theory to the Saving Based Vehicle Routing Algorithm, Civil Engineering Systems, 8(2), 87-93. 10.1080/02630259108970611

Tsoukalas L. H., Uhrig R. E. (1997), Fuzzy and Neural Approaches in Engineering, Wiley.

Werner T., Helbing D. (2003), The Social Force Model Applied to Real Life Scenarios, Pedestrian and Evacuation Dynamics 2003, Proceedings of the 2nd International Conference, 17-26. 12741139

Zadeh L. A. (1975), The Concept of Linguistic Variable and Its Application to Approximate Reasoning, Information Sciences, 8(3), 199-249. 10.1016/0020-0255(75)90036-5

각주

[6] 1) 샘플의 보행속도는 0.1-1.7m/s로 나타나 이를 17개 구간으로 나누어 빈도수를 비교함.

[7] 2) 이동방향 변화량은 1초 단위의 개별보행자 진행방향 차이를 의미하며 변화량 계급은 5° 단위로 구분함.

Journal of Korean Society of Transportation ISSN:1229-1366(Print) 2234-4217(Online) 대한교통학회지

Preview

Modeling Pedestrian Movement Behavior Using Social Force Model and Fuzzy Inference

ABSTRACT

MAIN

(1)

(2)

(3)

Table 1.

IF-THEN rules for modeling pedestrian movement behavior

Table 2.

Membership functions

Table 3.

Attribute weights

Figure 1

The contour lines representing the likelihood of changing walking direction or speed

Table 4.

Calculating likelihood of changing walking direction or speed

Figure 2

Pedestrian traffic flow relationship (macroscopic approaches)

Table 5.

Characteristics of the macroscopic pedestrian traffic flow (observational data)

Figure 3

Macroscopic characteristics of pedestrian flows

Table 6.

Validation results

Figure 4

Distribution of speed

Table 7.

Microscopic characteristics of pedestrian

Figure 5

Distribution of walking direction

References

각주