Performance Measurement and Determination of Introduction Criteria for Peak Demand Responsive Transit Service

Sedong Moon; Dong-Kyu Kim; Seung-Young Kho; Shin-Hyung Cho

doi:10.7470/jkst.2021.39.1.100

Preview

Article

Journal of Korean Society of Transportation. 28 February 2021. 100-114
https://doi.org/10.7470/jkst.2021.39.1.100

Performance Measurement and Determination of Introduction Criteria for Peak Demand Responsive Transit Service

첨두 수요 응답형 대중교통 서비스의 효과평가 및 도입 기준 수립

Sedong MOON¹

Dong-Kyu KIM²

Seung-Young KHO³

Shin-Hyung CHO⁴^*

문 세동¹

김 동규²

고 승영³

조 신형⁴^*

¹The Ph.D. Program, Department of Civil and Environmental Engineering, Seoul National University, Seoul 08826, Korea

²Associate Professor, Department of Civil and Environmental Engineering, Seoul National University, Seoul 08826, Korea

³Professor, Department of Civil and Environmental Engineering, Seoul National University, Seoul 08826, Korea

⁴Researcher, School of Civil and Environmental Engineering, Geogia Institute of Technology, GA 30332, USA

¹서울대학교 건설환경공학부 석박사통합과정

²서울대학교 건설환경공학부 부교수

³서울대학교 건설환경공학부 교수

⁴조지아공과대학교 건설환경공학부 박사후연구원

^{*Corresponding Author}

ABSTRACT

Peak demand responsive transit (peak DRT) services are being proposed recently to supplement urban public transportation systems’ limitations. The peak DRT aggregates passengers with similar origins, destinations, and departure times into groups and provides a demand-responsive and express service for each group. This study evaluated the performance of introducing the peak DRT, then established the criteria to determine O-D pairs to introduce the DRT service. To achieve this, we assumed that the DRT should be introduced for O-D pairs with great demands and inferior public transportation services and identified O-D pairs to introduce the DRT under varying criteria: the minimum demand and the minimum difference of generalized travel time between private car and public transportation. We clustered individual public transportation trips on smartcard data by origins, destinations, and departure times, then generated a DRT route for each cluster and evaluated its cost and benefit. This procedure was repeated under varying criteria, and a criterion that maximizes the benefit-to-cost (B/C) ratio or maximizes the benefit while maintaining B/C at least one was selected. As a result, the number of DRT passengers as well as the benefit of DRT introduction were higher under a criterion maximizing the benefit than a criterion maximizing the B/C. This result implies that the criterion for peak DRT introduction should be determined to maximize the benefit than the B/C to provide the DRT service for more people.

Keywords

demand-responsive transportation (DRT)

introduction criteria

peak demand responsive transit service (peak DRT)

performance evaluation

smartcard data

도시 대중교통 시스템의 한계점을 보완하기 위하여, 기점, 종점, 출발시각이 유사한 승객들을 하나의 그룹으로 묶고, 각 그룹 단위로 수요에 응답하면서도 급행처럼 빠른 서비스를 제공하는 첨두 수요 응답형 대중교통 서비스(첨두 DRT)가 최근 제안되고 있다. 본 연구에서는 첨두 DRT에 대해 도입 효과를 평가하고, 이를 기반으로 DRT를 어떠한 O-D 쌍에 도입할지를 결정하기 위한 기준을 수립하였다. 이를 위하여 본 연구에서는 수요가 많으면서 대중교통 서비스가 불량한 O-D 쌍에 DRT를 도입하는 것으로 가정하고, DRT의 도입 기준이 되는 수요의 최솟값 및 대중교통과 승용차의 일반화 통행시간 차의 최솟값을 여러 가지로 변화시키면서 DRT를 도입할 O-D 쌍들을 판별하였다. 그리고 스마트카드 데이터에 나타난 개별 대중교통 통행을 기점, 종점, 출발시각에 따라 클러스터링한 뒤, 각 클러스터 단위로 DRT 노선을 생성하고 그 비용과 편익을 산출하였다. 이를 DRT 도입 기준을 변화시키면서 반복하였으며, 비용 대 편익 비(B/C)를 최대화하거나, B/C를 1 이상으로 유지하면서 편익을 최대화하는 기준을 최적의 DRT 도입 기준으로 선정하였다. 그 결과 B/C를 최대화할 때에 비해서 편익을 최대화할 때 DRT의 편익뿐만 아니라 DRT를 이용하는 승객 수 역시 더 높게 나타났다. 이는 실제 DRT 도입 시 편익을 최대화하는 방향으로 도입 기준을 수립하는 것이 B/C를 최대화하는 방향에 비해 더 많은 사람들에게 DRT 서비스를 제공한다는 측면에서 좀 더 바람직함을 의미한다.

키워드

수요응답형 교통체계(DRT)

첨두 수요 응답형 대중교통 서비스(첨두 DRT)

도입 기준

효과평가

스마트카드 데이터

MAIN

서론
선행연구
연구 방법
1. DRT 서비스를 도입하기 위한 O-D 쌍의 결정
2. O-D 쌍 클러스터링
3. DRT 경로 생성 및 효과평가
사례연구
1. 네트워크 및 분석 데이터
2. DRT 서비스 도입 기준 선정결과
논의
1. DRT 서비스 도입 전략
2. 민감도 분석
결론

서론

대중교통은 그 경로 및 시간표가 고정되어 있어 다른 교통수단에 비해 편의성이 낮은 편이다. 이것은 자가용 및 택시 이용자들에게 대중교통으로 수단을 전환할 만한 충분한 매력을 제공하지 못한다. 특히 카셰어링이나 라이드셰어링 같이 개인화된 서비스를 제공할 수 있는 새로운 모빌리티 서비스가 등장하면서 개인화된 서비스를 제공하지 못하는 대중교통의 매력도는 더욱 감소하였다. 그러나 대중교통은 이산화탄소 및 오염물질의 배출과 에너지 소비가 적은 효율적인 교통수단이므로 현재의 대중교통 수요를 유지함과 동시에 자가용 및 택시 이용자를 대중교통 또는 그와 비슷한 수단으로 전환시킬 필요가 있으며, 따라서 대중교통의 단점은 해결될 필요가 있다.

이를 위해, 자가용처럼 편리하면서 현재의 대중교통처럼 효율적인 새로운 서비스가 필요하다. 이 서비스는 기존의 대중교통보다 통행시간이 짧고 환승횟수가 적으면서도 현재의 대중교통처럼 다량의 수요를 처리할 수 있어야 한다. 수요응답형 교통체계(demand-responsive transportation, DRT) 및 급행 서비스는 이 조건을 만족한다. DRT는 고정된 경로나 시간표 없이 이용자의 수요가 발생했을 때 이에 맞춰서 운행되며, 따라서 기존의 대중교통보다 이용자의 환승 횟수 및 환승에 소요되는 시간이 줄어든다. 또한, 급행은 기존 대중교통 노선에서 정류장의 개수를 줄임으로써 이용자의 차내시간을 단축한다.

일반적으로 DRT는 농어촌 등 통행 수요의 밀도가 낮은 지역에서 발생하는 대중교통 운영의 비효율을 해결하기 위해 도입되며, 수요의 밀도가 높은 도시 지역에서는 DRT에 비해 대중교통이 더 효율적임이 알려져 있다(Diana et al., 2009; Quadrifoglio and Li, 2009; Li and Quadrifoglio, 2010; Edwards and Watkins, 2013; Navidi et al., 2018). 그러나 도시에서의 대중교통 시스템은 통행시간 및 편의성 측면에서 모든 승객을 만족시키기는 어려우며, 특히 일부 기종점쌍(origin-destination pair, O-D 쌍)에 대해서는 통행시간이 길거나 환승이 많이 필요하여 대중교통 통행이 불편해지는 경우도 발생한다. 이러한 도시 대중교통의 한계점을 보완하기 위하여, 기점, 종점, 출발시각이 유사한 승객들을 하나의 그룹으로 묶고 각 그룹 단위로 서비스를 제공함으로써 수요에 응답하면서도 도시에서 자주 나타나는 첨두 시 수요를 한 번에 처리할 수 있는 도시 대중교통으로서의 DRT 서비스가 제안되고 있다(Lyu et al., 2016, 2019; Ma et al., 2017; Li et al., 2018; Chen et al., 2018; Guo et al., 2018, 2019; Zheng et al., 2019). 선행 연구에서는 이러한 서비스를 ‘맞춤형 버스(customized bus, CB)’ 또는 ‘대규모 첨두 수요응답형 고속 셔틀(large-scale instantaneous peak demand responsive express shuttle)’ 등의 여러 명칭으로 지칭하고 있으며, 본 연구에서는 첨두 시간대의 통행 수요에 응답하는 대중교통이라는 점에서 ‘첨두 수요 응답형 대중교통 서비스(이하 첨두 DRT)’라고 칭하고자 한다. 첨두 DRT는 “기점 구역”과 “종점 구역”으로 지정된 구역 내의 정류장에서만 정차하며 각 정류장은 이용자들의 출발지와 도착지에 가깝게 배치되어 있어서 도보 거리가 짧으면서 환승도 필요하지 않은 문전 수송(door-to-door) 서비스를 제공할 수 있다(Liu and Ceder, 2015). 또한, 기점 구역과 종점 구역 사이에서는 정차하지 않거나 적은 수의 정류장에만 정차함으로써 급행처럼 빠른 서비스를 제공할 수 있다(Lyu et al., 2019).

현재까지의 첨두 DRT에 대한 연구는 주로 정류장 선택, 노선 계획, 경로 선정을 중심으로 이루어져왔으며, 첨두 DRT의 도입 효과를 평가하고 DRT를 어떠한 O-D 쌍에 도입할지를 결정하기 위한 연구는 아직 부족한 상황이다. 따라서, 본 연구에서는 첨두 DRT에 대해 효과평가를 수행하고, 이를 기반으로 DRT 서비스를 도입하기 위한 기준을 결정하는 것을 목적으로 한다. 이를 위하여 수요가 많으면서 대중교통 서비스가 불량한 O-D 쌍에 DRT를 도입하는 것으로 가정하고, DRT의 도입 기준을 여러 가지로 변화시키면서 DRT를 도입할 O-D 쌍들을 판별한다. 여기서 대중교통 서비스는 이용자의 일반화된 통행시간(generalized travel time)으로 평가하며, 여기에는 통행시간 및 환승 페널티가 포함된다. 다음으로, 기점, 종점, 출발시각이 비슷한 O-D 쌍들을 클러스터링한 뒤 각각의 클러스터별로 DRT 노선을 생성한다. 여기서 DRT의 수요는 현재의 대중교통 수요에 비례하는 것으로 가정하며, 그 전환율은 여러 가지 시나리오로 설정한다. 그리고 각각의 DRT 도입 기준에 대해 이용자, 운영자, 사회적 비용 및 편익을 산정한 뒤, 여러 가지 DRT 도입 기준의 비용과 편익을 비교함으로써 최적의 도입 기준을 결정한다.

본 논문의 구성은 다음과 같다. 먼저 DRT 서비스에 대한 선행연구를 고찰하며, 특히 첨두 DRT 서비스에 대해 중점적으로 다룬다. 그 뒤, 본 연구의 방법론과 이 방법론을 실제 데이터에 대해 적용한 결과에 대하여 설명한다. 그리고 논의와 본 연구의 결론에 대하여 언급할 것이다.

선행연구

DRT는 크게 dial-a-ride(DAR), 지선 서비스(feeder service), 첨두 DRT 등 세 가지 유형으로 분류할 수 있다. 먼저 DAR은 협의의 DRT로 볼 수 있으며 요청이 발생하는 대로 차량이 배차되는 시스템이다. DAR은 주로 농어촌 지역에서 낮은 빈도로 나타나는 개별 수요를 처리하는 데 적합하며, 도시에서 나타나는 대량의 동시다발적 수요를 처리하는 데는 부적합하다(Zheng et al., 2019). 그리고 지선 서비스는 개별 이용자들의 기점이나 종점을 간선 대중교통 정류장(철도역 또는 간선버스 정류장)과 연계하는 라스트 마일(last-mile) 서비스이다(Quadrifoglio et al., 2008; Quadrifoglio and Li, 2009; Li and Quadrifoglio, 2010; Beaudry et al., 2010; Edwards and Watkins, 2013). 지선 서비스는 개별 이용자의 기점과 종점을 직접 연결하지 않으므로 환승을 필요로 한다. 그러나 첨두 DRT는 DAR 및 지선 서비스와는 달리 승하차 정류장을 기점 구역과 종점 구역 내로 제한함으로써 유사한 통행 수요를 통합하고 대량의 수요를 처리할 수가 있다. 또한, 중간 정차를 최소화함으로써 DAR 및 지선 서비스에 비해 차내시간이 단축된다. DAR 및 지선 서비스의 경로 선정 및 스케줄링 방법론에 대해서는 많은 연구에서 다루어 왔으며(Quadrifoglio et al., 2008; Diana et al., 2009; Quadrifoglio and Li, 2009; Li and Quadrifoglio, 2010; Beaudry et al., 2010; Edwards and Watkins, 2013; Navidi et al., 2018), 첨두 DRT에 대해서는 최근 들어 방법론이 개발되는 추세이다.

첨두 DRT에 대한 정류장 선택, 노선 계획, 경로 선정 등을 수행한 선행 연구는 다음과 같다. Ma et al.(2017)은 bottom-up clustering 방법으로 기점 및 종점을 클러스터링하여 기점 및 종점 구역을 선정하였다. 해당 연구에서는 단순히 두 구역을 연결한 것을 DRT 노선으로 간주하였다. 이 중 최소 노선 길이 제약을 만족하면서 운영 비용, 환경 비용, 교통 혼잡 비용의 총합을 최소로 하는 DRT 노선들의 조합을 탐색하였다. Li et al.(2018)은 버스 정류장들을 기점 및 종점 구역들로 클러스터링한 뒤, 최소 수요 및 거리 기준을 만족하는 O-D 쌍들에 DRT를 도입하는 것으로 선정하였다. Chen et al.(2018)은 수요가 발생한 지점들을 클러스터링하여 DRT 정류장으로 선정하였으며, 각 정류장의 영향권은 반경 200-500m로 설정하였다. 그 뒤 DRT에 의해 수송되는 인원을 최대화하면서 통행시간의 합을 최소화하는 노선을 유전알고리즘을 통해 설계하였다. Lyu et al.(2016, 2019)은 교통 수요 클러스터링, 정류장 배치, 노선 계획의 3단계 과정을 거쳐서 DRT의 총 이익을 최대화하였다. 각 단계에서 grid-density based clustering, k-medoid 및 동적 프로그래밍 알고리즘을 적용하였다. Guo et al.(2018)은 유전 알고리즘을 이용하여 이용자 비용과 차량 운영 비용의 총합을 최소화하는 DRT 노선을 설정하였다. 같은 연구자들에 의한 다른 연구(Guo et al., 2019)에서는 time window 제약을 추가하고 서비스를 이용하지 못한 승객에 대한 페널티를 추가하였다. Zheng et al.(2019)은 전체 수요를 서비스 단위(service unit)들로 분류하고 각각의 서비스 단위마다 차량 배정, 경로 설정, 시간표 설정을 시행하여 운영 비용을 최소화하였다. 이와 같이, 지금까지의 첨두 DRT 계획을 위한 연구에서는 대부분 통행 수요를 기점, 종점, 출발 시각이 비슷한 것끼리 클러스터링하여 서비스 단위로 분류한 뒤, DRT의 경로나 스케줄을 각 서비스 단위별로 최적화하였다.

선행 연구에서는 DRT의 효과평가 및 대중교통과의 비교 역시 수행되었으며, 그 사례는 다음과 같다. Diana et al.(2009)은 대중교통과 DAR의 통행거리, 통행시간, 대기시간, 환승 승객의 비율을 여러 가지 시나리오(네트워크 형태, 대중교통 운행 빈도, 수요의 밀도 등)에 대해 비교하였다. Navidi et al.(2018)은 대중교통과 DAR의 통행시간과 운영 비용을 여러 시나리오에 대해 비교하였다. 해당 연구에서는 각 통행자의 통행을 시뮬레이션할 때 행위자 기반 교통 시뮬레이션 및 동적 경로생성(dynamic routing)을 이용하였다. Quadrifoglio and Li(2009) 및 Li and Quadrifoglio(2010)에서는 총비용, 도보시간, 대기시간, 차내시간을 대중교통과 지선 서비스 형태의 DRT에 대해 비교하였다. 해당 연구에서 도로의 네트워크는 격자형, 대중교통 노선은 직선으로 가정하고, 서비스 존의 크기, 수요의 밀도, 도보시간의 가치, 차량의 운행비용에 따라 시나리오를 세워서 대중교통과 지선 서비스에 대한 시뮬레이션을 수행하였다. Edwards and Watkins(2013)에서는 실제 도로 네트워크의 대중교통과 지선 서비스에 대해서 통행시간과 운영 비용을 비교하였다. 해당 연구에서는 대중교통과 지선 서비스에 대해 네트워크 형태에 영향을 주는 지역 및 여러 가지 수요 밀도에 대해 시뮬레이션하였다. DRT의 효과를 평가하고 대중교통과 비교한 지금까지의 연구에서는 수요의 밀도가 낮을 때는 DRT가 유리하며, 수요의 밀도가 높을 때는 대중교통이 유리하다는 결과가 도출되었다. 이는 수요의 밀도가 낮은 지역에 DRT가 도입되어야 함을 시사하고 있다. 그러나 이러한 결과는 DAR 및 지선 서비스 형태의 DRT에만 국한된 것이며, 본 연구에서 다룰 첨두 DRT에 대해서는 DRT의 효과평가를 수행하거나, DRT를 대중교통과 비교함으로써 어떠한 지역 및 O-D 쌍에 도입되어야 하는지를 결정한 연구가 아직 부족하다.

현재까지 DAR 및 지선 서비스 형태의 DRT에 대해서는 경로 및 스케줄을 최적화하는 연구 및 효과평가를 수행하고 어떤 지역 또는 O-D 쌍에 도입되어야 하는지를 결정하는 연구가 수행되었다. 이에 비해 첨두 DRT에 대해서는 정류장 선택, 노선 계획, 경로 선정 등에 대한 연구가 주로 이루어졌으나, 효과평가를 수행하고 어떤 O-D 쌍에 도입할지를 결정한 연구는 부족한 상황이다. 따라서 본 연구에서는 첨두 DRT에 대해 효과평가를 수행하고, 이를 기반으로 첨두 DRT를 도입하기 위한 O-D 쌍을 결정하는 기준을 제시하고자 한다.

연구 방법

본 연구에서의 첨두 DRT는 Figure 1과 같이 기점, 종점, 출발시각이 유사한 개별 통행자들의 기점들을 기점 구역(origin area), 종점들을 종점 구역(destination area)으로 클러스터링함으로써 O-D 클러스터들을 생성하고, 각 O-D 클러스터 단위로 수요응답형 서비스를 제공하는 것으로 가정한다. 또한, 본 연구에서 DRT를 도입하기 위한 O-D 쌍들을 결정하고, O-D 쌍 클러스터링을 시행하며, DRT의 경로를 생성하고 효과평가를 수행하는 과정을 요약하면 Figure 2와 같다.

https://static.apub.kr/journalsite/sites/kst/2021-039-01/N0210390108/images/kst_39_01_08_F1.jpg

Figure 1

Schematic diagram of a peak DRT service

https://static.apub.kr/journalsite/sites/kst/2021-039-01/N0210390108/images/kst_39_01_08_F2.jpg

Figure 2

Procedure of this study’s methodology

1. DRT 서비스를 도입하기 위한 O-D 쌍의 결정

본 연구에서는 DRT 서비스가 대중교통의 서비스가 불량하면서 수요가 많은 O-D 쌍에 도입되어야 한다고 가정한다. 여기서 서비스가 불량하다는 것은 대중교통 통행 시 승용차에 비해 오랜 시간이 소요되거나 환승이 많이 필요한 것을 의미한다. 본 연구에서 O-D 쌍의 대중교통의 서비스는 대중교통과 승용차의 ‘일반화 통행시간’의 차이를 통해 평가하며, 일반화 통행시간은 Equations 1,2,3과 같이 차내시간과 환승횟수를 통해 산정한다.

(1)

G T_{t} = t_{t} + p_{t r a n s} n_{t}

(2)

G T_{a} = t_{a}

(3)

△ G T = G T_{t} - G T_{a}

여기서, $G T_{t}$ 와 $G T_{a}$ 는 각각 대중교통과 승용차의 일반화 통행시간이며, $t_{t}$ 와 $t_{t}$ 는 각각 대중교통과 승용차의 차내시간이며, $p_{t r a n s}$ 는 ‘환승 페널티’로서 1회의 환승으로 인해 이용자가 느끼는 불편을 동등한 수준의 추가 차내시간으로 표현한 값이다. $n_{t}$ 는 환승 횟수이며 $△ G T$ 는 일반화 통행시간의 차이이다. 하나의 O-D 쌍에 대한 대중교통 통행의 차내시간 및 환승 횟수는 개개인에 따라 달라질 수 있으며, 본 연구에서는 이를 O-D 쌍별로 평균한 것을 및 $n_{t}$ 의 값으로 적용하였다. 또한, Equation 3에서 볼 수 있듯이, $△ G T$ 의 값이 클수록 대중교통 서비스가 불량함을 의미한다.

DRT가 도입되면 대중교통 수요 중 일부가 DRT로 전환될 것으로 기대할 수 있다. 이때의 수요 전환량은 통행시간, 대기시간, 접근시간, 요금, 서비스 이용 편의성, 차내혼잡, 환승 횟수, 운행 시간표 등 다양한 요소에 영향을 받는다. 그러나 이러한 요소들이 대중교통과 DRT 사이의 수단 선택에 미치는 영향에 대해서는 기존의 승용차, 버스, 철도 등에 대해 개발되어 있는 수단 선택 모형을 그대로 적용하기 곤란하며, DRT에 대해서는 아직 국내에서 공인된 수단 선택 모형이 개발되어 있지 않은 실정이다. 따라서 본 연구에서는 대중교통 수요 중에서 일정 비율이 DRT로 전환된다고 가정하였으며, 그 비율에 대해서는 5가지 시나리오를 수립하여 시나리오 1에서 10%, 시나리오 2에서 20%, 시나리오 3에서 30%, 시나리오 4에서 40%, 시나리오 5에서 50%로 가정하였다. 또한, 대중교통에서 DRT로의 수단 전환은 모든 O-D 쌍에서 동일한 비율로 전환된다고 가정하였다. 이후 DRT 서비스를 도입할 O-D 쌍을 결정하였으며, 본 연구에서 DRT는 Equation 4와 같이 $△ G T$ 의 값 및 DRT의 수요가 어떤 특정 기준보다 큰 O-D 쌍 $(O, D)$ 에 도입되는 것으로 한다.

(4)

Δ G T_{(O, D)} \geq Δ G T_{m i n} a n d D_{(O, D)} \geq D_{m i n}

여기서, $Δ G T_{(O, D)}$ 와 $Δ G T_{m i n}$ 은 각각 O-D 쌍 $(O, D)$ 의 $△ G T$ 와 DRT를 도입하기 위한 $△ G T$ 의 최솟값이며, $D_{(O, D)}$ 와 $D_{m i n}$ 은 각각 O-D 쌍 $(O, D)$ 의 DRT 수요와, DRT를 도입하기 위한 DRT 수요의 최솟값이다. 이에 따라 DRT의 도입 기준은 순서쌍 $(Δ G T_{m i n}, D_{m i n})$ 으로 표현할 수 있다. 본 연구에서 $△ G T_{m i n}$ 은 상위 20% 값에서 상위 5% 값까지로 하였으며, $D_{m i n}$ 은 상위 30% 값에서 상위 1% 값까지로 하였다.

2. O-D 쌍 클러스터링

첨두 DRT의 효율적인 운영을 위해서는 유사한 통행 수요끼리 군집화하는 것이 중요하다. 본 연구에서는 이를 O-D 쌍 클러스터링 과정을 통해 수행한다. 클러스터의 크기(클러스터당 원소의 개수)는 차량 경로 생성 문제(vehicle routing problem, VRP)에 소요되는 계산 시간을 단축하기 위해서 충분히 작아야 한다. 그러면서도 한 클러스터의 승객 수가 차량 한 대의 용량보다 적다면 비효율이 발생하므로, 클러스터당 수요는 최소한 차량 한 대의 용량 이상은 되어야 한다. 두 가지를 모두 고려하면 클러스터당 수요는 차량 한 대의 용량 수준으로 일정하여야 한다. 본 연구에서는 비교적 균등한 크기의 O-D 쌍 클러스터를 생성하기 위해, 계층적 군집화(hierarchical clustering)의 한 방법인 iterative dichotomy(R Documentation, 2019)를 사용하였다. 이 방법은 다음과 같으며, 비교적 간단하면서도 균등한 크기의 클러스터를 만들 수 있다는 장점이 있다.

Step 1. 처음에 모든 원소(O-D 쌍)는 동일한 클러스터에 속한다.

Step 2. 만약 차량 한 대의 용량보다 수요가 많은 클러스터가 있다면, 그 중 가장 수요가 많은 클러스터를 다음과 같은 과정을 통해 두 개로 분할한다.

Step 2-1. 다음과 같은 과정으로 계층적 군집화 트리(hierarchical clustering tree)를 생성한다.

Step 2-1-1.모든 원소 간의 거리 메트릭(distance metric)을 측정한다. 본 연구에서는 원소들이 단일 점이 아니라 O-D 쌍임을 고려하여, O-D 쌍들의 기점 사이의 거리와 종점 사이의 거리의 합을 거리 메트릭으로 간주하였다.

Step 2-1-2. 거리가 가장 가까운(거리 메트릭의 값이 가장 작은) 두 개의 원소를 하나의 새로운 O-D 쌍으로 통합하고, 통합된 원소의 기점 및 종점의 좌표는 원래 원소들의 기점 및 종점 좌표의 평균으로 한다. 통합되기 전의 원소들과 그들 사이의 거리 메트릭 값을 트리에 표시한다.

Step 2-1-3. 모든 원소가 통합될 때까지 Step 2-1-2처럼 가장 가까운 두 개의 원소를 통합하는 작업을 반복한다.

Step 2-2. 군집화 트리를 맨 위에서 양쪽으로 나눈다.

Step 2-3. 나뉜 각 트리에 속한 원소들은 새로운 클러스터로 분류된다.

Step 3. 모든 클러스터의 수요가 차량 한 대의 용량보다 낮아질 때까지 Step 2를 반복한다.

3. DRT 경로 생성 및 효과평가

본 연구에서는 DRT 차량은 현재 존재하는 대중교통 정류장(버스정류장 및 지하철역)에서 승객을 태우거나 내리는 것으로 가정하였다. 실제 대중교통 네트워크에서는 서로 반대 방향의 버스정류장이 도로를 사이에 두고 마주보는 경우가 많으며 이 경우 두 정류장은 같은 정류장으로 취급할 수 있다. 또한, 지하철역의 경우에는 거의 모든 지하철역이 근처에 버스정류장을 동반하며, 이 경우 근처 버스정류장에 DRT 차량을 정차시킴으로써 DRT와 지하철역의 연계가 가능하다. 이 점을 고려하여 대중교통 정류장들은 density-based spatial clustering of applications with the noise(DBSCAN) 알고리즘(Ester et al., 1996)으로 클러스터링함으로써 정류장 군집을 생성하였다. DBSCAN의 수행 과정은 다음과 같다.

Step 1. 주어진 모든 점들에 대해 반지름 ε 안에 있는 점의 개수를 센다. 만약 어떤 점 p를 중심으로 하고 반지름이 ε인 원 안에 minPts개 이상의 점이 포함된다면, 점 p는 core point가 되며 원 안에 포함되는 다른 점들은 p와 같은 군집으로 묶인다. 여기서 ε 및 minPts는 사전에 정의되어야 한다.

Step 2.만약 점 p₁을 중심으로 하는 군집 안에 다른 core point p₂가 포함된다면, p₁을 중심으로 하는 군집과 p₂를 중심으로 하는 군집은 한 군집으로 통합된다.

Step 3. Step 2를 모든 core point에 대해서 수행한다.

Step 4. 어느 군집에도 속하지 않는 점들은 노이즈로 취급한다.

본 연구에서 DBSCAN을 수행할 때 도로의 폭이 최대 100m를 넘지 않는다는 것을 고려하여 ε=100m으로 설정하였으며, 왕편과 복편이 일치하지 않는 일부 버스 노선은 버스 정류장이 도로 한 쪽에만 존재할 수도 있으며 이 경우는 별도의 독립된 정류장으로 취급되어야 한다는 점을 고려하여 minPts=1로 설정하였다. 클러스터링 이후에는 각 정류장 군집마다 군집에 소속된 정류장들의 기하학적 중심을 DRT 차량의 정류장으로 간주하고 각각의 O-D 클러스터에 대해 DRT 차량의 경로를 생성하였다. 여기서 경로 생성의 목적함수는 운행 거리를 최소화하는 것으로 하였다. 차량의 경로를 생성하는 문제(vehicle routing problem, VRP)는 NP-난해(NP-hard) 최적화 문제로서 전역(global) 최적해를 구하는 데에는 많은 계산 시간이 소요되고, 따라서 휴리스틱 알고리즘으로 해결하는 것이 일반적이다. 본 연구에서는 초기 해 탐색에는 평행 최소비용 삽입(parallel cheapest insertion) 알고리즘(Chapleau et al., 1984)을 사용하였으며, 이 알고리즘은 주어진 링크를 현재의 차량 운행 노선에 삽입하고자 할 때, 삽입 후 우회로 인해 발생하는 노선의 길이 증가가 최소화되도록 삽입한다. 또한, 지역해 탐색 과정에는 타부 서치(tabu search) 알고리즘(Glover, 1989, 1990)을 사용하였다. 타부 서치는 지역 탐색(local search) 과정에서 현재 해의 주변에 있는 모든 해를 탐색한 뒤 이전 단계의 해는 타부 리스트(tabu list)라는 목록으로 저장하여 더 이상 탐색하지 않도록 한 것이며, 그 구체적인 수행 과정은 다음과 같다.

Step 1. 현재 후보 해 $x_{c}$ 의 주변에 있는 해 중 타부 리스트에 등재되지 않은 해 $x$ 에 대해서 다음을 반복한다.

Step 1-1. 목적함수를 $f (x)$ 를 최소화하고자 하는 경우, $f (x) < f (x_{c})$ 일 때 $x_{c}$ 의 값을 $x$ 로 변경한다.

Step 2. 현재까지의 최적해를 $x^{*}$ 라고 하면, $f (x_{c}) < f (x^{*})$ 일 때 $x^{*}$ 의 값을 $x_{c}$ 로 변경한다.

Step 3. $x_{c}$ 는 탐색을 수행한 해이므로 타부 리스트에 등재하여 더 이상 탐색하지 않도록 한다.

Step 4. Step 1-Step 3을 정해진 반복 종료 조건을 만족할 때까지 반복한다.

DRT 경로 생성 이후에는 DRT 도입의 편익 및 비용을 산정하여 DRT 도입의 효과를 평가하였다. 편익은 Equations 5-6과 같이 DRT를 이용한 개별 이용자의 일반화 통행 비용의 감소량을 구한 뒤, 그 총합으로 산정하였다.

(5)

B^{i} = G C_{t}^{i} - G C_{d}^{i}

(6)

G C_{t}^{i} = V O T (G T_{t}^{i})

여기서, 는 대중교통에서 DRT로 수단 전환된 이용자 i의 편익이고, $G C_{t}^{i}$ 와 $G C_{d}^{i}$ 는 각각 이용자 의 대중교통 및 DRT 이용 시의 일반화 통행 비용이며, $V O T$ 는 통행시간가치이고, $G T_{t}^{i}$ 와 $G T_{d}^{i}$ 는 각각 이용자 i의 대중교통 및 DRT 이용 시의 일반화 통행시간이다. DRT 이용 시에는 개별 이용자의 기점과 종점이 한 노선으로 연결되므로 환승은 없다고 간주하였으며, 이에 따라 DRT 이용 시의 일반화 통행시간인 $G T_{d}^{i}$ 는 Equations 7 -8과 같이 DRT의 차내 시간(주행 시간과 정차 시간의 합)으로 산정하였다.

(7)

G C_{d}^{i} = V O T (G T_{d}^{i}) = V O T (t_{d}^{i}) = V O T (\frac{l_{d}^{i}}{v_{d}} + \sum_{S \equiv P_{i}}^{} s (S))

(8)

s (S) = δ + m a x (τ_{b} b (S), τ_{a} a (S))

여기서, $t_{d}^{i}$ 및 $l_{d}^{i}$ 는 각각 DRT를 탑승한 이용자 i의 차내시간과 통행거리이고, $v_{d}$ 는 DRT 차량의 주행 속도이며, $S$ 는 DRT 정류장이고, $P_{i}$ 는 DRT를 탑승한 이용자 i의 이동 경로이며, 는 정류장 $S$ 에서의 DRT 차량의 정차 시간이다. $d e l t a$ 는 매 정류장마다 DRT 차량의 가속, 감속, 문 열기 및 문 닫기로 인한 시간 지연이며, $τ_{b}$ 및 $τ_{a}$ 는 각각 승차 및 하차 승객 1명마다 소요되는 정차 시간이고, $b (S)$ 및 $a (S)$ 는 각각 정류장 $S$ 에서의 승차 및 하차 승객 수이다.

또한, 비용은 Equation 9와 같이 개별 DRT 노선의 비용을 구한 뒤, 이를 네트워크상의 모든 DRT 노선에 대해 합산하였다. 개별 DRT 노선의 비용은 차량의 운행 거리에 비례하는 것으로 가정하였다.

(9)

C^{r} = L^{r} (c_{o} + c_{s})

여기서, $C^{r}$ 및 $L^{r}$ 은 각각 DRT 노선 r의 비용 및 길이이며, $c_{o}$ 및 $c_{s}$ 는 각각 DRT 차량의 단위 운행 거리당 운영자 비용 및 사회적 비용이다.

본 연구에서는 두 가지 방법으로 DRT의 최적 도입 기준을 결정하였다. 첫 번째 방법은 비용 대 편익비(benefit-to-cost ratio, B/C)를 최대화하는 것이다. B/C는 편익을 비용으로 나눈 값으로, 클수록 투자 대비 편익이 많이 발생함을 의미한다. 두 번째 방법은 타당성을 유지하는(즉, B/C≥1) 한에서 편익의 크기를 최대화하는 것이다.

사례연구

1. 네트워크 및 분석 데이터

본 연구에서는 앞서 설명한 방법론을 실제 도시의 교통 네트워크 및 데이터에 적용하는 사례연구(case study)를 진행하였다. 사례연구의 공간적 범위는 서울시, 시간적 범위는 2017년 5월 16-22일 중 평일(16, 17, 18, 19, 22일) 오전 첨두 시간대(오전 7-9시)로 하였다. 이를 위해 대중교통의 통행시간 및 환승 횟수 데이터, 승용차 통행시간 데이터, 대중교통 정류장의 공간 정보, 도로 네트워크의 공간 정보를 사용하였다.

먼저 대중교통의 통행시간 및 환승 횟수는 2017년 5월 평일 오전 7-9시의 스마트카드 데이터에서 추출하였다. 스마트카드 데이터는 각각의 대중교통 통행에 대해 이용한 수단, 노선 번호, 승차 시각 및 정류장, 하차 시각 및 정류장, 이동거리, 차내시간, 환승횟수 등의 정보를 포함하고 있다. 특히 환승이 발생한 경우 개별 수단통행을 목적통행별로 집계하여 통행사슬(trip chain) 데이터로 변환할 수 있으며, 이 경우에는 한 번의 목적통행이 이루어지는 동안 발생한 환승의 횟수, 환승한 정류장, 환승에 소요된 시간 등을 알 수 있다. 본 연구에서는 스마트카드 데이터를 통행사슬로 변환한 데이터를 사용하였으며, 5일 간의 오전첨두 시간대에 발생한 9,172,359건의 수단통행 및 6,847,672건의 목적통행에 대하여 분석을 수행하였다.

승용차 통행시간은 평일의 같은 시간대(오전 9시 도착)에 대한 자동차 내비게이션 길찾기 데이터(T map API)에서 추출하였다. 내비게이션 데이터는 주어진 출발지 및 도착지 사이의 최적 길찾기 결과 및 예상 통행시간을 포함하고 있다. 본 연구에서는 서울시내 424개 행정동의 동별 중심 좌표를 출발지 또는 도착지로 하는 179,776개의 O-D 쌍에 대한 승용차 통행의 길찾기 결과 및 통행시간을 사용하였다.

대중교통 정류장의 공간 정보는 서울시내 버스정류장 및 지하철역의 경위도 좌표를 포함하고 있다. 서울시내 버스정류장의 개수는 46,949개, 지하철역의 개수는 376개이며 DBSCAN 수행 결과 3,953개의 정류장 군집이 생성되었다. 그리고 3,953개의 정류장 군집 사이의 O-D 쌍들 중 실제로 대중교통 통행이 발생한 O-D 쌍의 개수는 694,732개로 나타났다. 또한, 도로 네트워크의 공간 정보는 DRT 정류장 사이의 도로 상 거리를 도출하는 데 사용하였으며, 이는 DRT 경로 생성에 활용되었다.

본 연구에서 사용한 파라미터에 적용된 값은 Table 1과 같다. 표에서 환승 페널티( $p_{t r a n s}$ ), 단위 거리당 운영자 비용( $c_{o}$ ) 및 사회적 비용( $c_{s}$ )은 선행 연구(Yoo, 2015; Jeon, 2016)의 값을 사용하였다. 통행시간가치( $V O T$ )는 교통시설 투자평가지침(Ministry of Land, Infrastructure and Transport, 2017)의 버스 통행에 대한 업무, 출근, 비업무 통행 시간가치를 수도권 오전첨두시의 업무, 출근, 비업무 통행 비율로 가중평균한 값을 사용하였다. 또한, 정류장 당 시간지연( $δ$ ), 승차 및 하차 승객 1인당 소요 시간( $τ_{b}$ , $τ_{a}$ )은 도로용량편람(Ministry of Land, Transport and Maritime Affairs, 2013)의 값을 사용하였다. 그리고 DRT 차량의 주행 속도( $v_{d}$ )는 내비게이션 데이터의 평일 오전 9시의 평균 승용차 통행 속도를 적용하였다. 또한, DRT 차량의 용량은 일반적인 도시형 버스 차량의 승객 정원을 고려하여 60인으로 가정하였다.

Table 1.

Values assigned to the parameters in this study

Parameter	Explanation	Value	Reference
$p_{t r a n s}$	Unit transfer penalty	11.24 min/transfer	Yoo (2015)
$V O T$	Value of time	7,656 won/hr	*
$δ$	Delay per stop	19 s	**
$τ_{b}$	Dwell time needed per each boarding passenger	3.2 s	**
$τ_{a}$	Dwell time needed per each alighting passenger	1.5 s	**
$c_{o}$	Operation cost per unit distance	2,240.1 won/km	Jeon (2016)
$c_{s}$	Social cost per unit distance	577.0 won/km	Jeon (2016)
$v_{d}$	Speed of DRT vehicle	23.6 km/h	***
Capacity of a DRT vehicle		60 passengers	****

*Ministry of Land, Infrastructure and Transport (2017)

**Ministry of Land, Transport and Maritime Affairs (2013)

***Observed value from navigation data

****Our assumption

2. DRT 서비스 도입 기준 선정결과

본 연구에서 DRT 서비스의 도입 기준을 설정한 결과는 Table 2와 같다. DRT를 도입하기 위한 O-D 쌍의 $△ G T$ 의 최솟값( $△ G T_{m i n}$ )들은 모든 시나리오에 대해 동일하게 설정되었으며, 수요의 최솟값( $D_{m i n}$ )들은 각각의 시나리오에 대해 다르게 설정되었다.

Table 2.

Introduction criteria of DRT service evaluated in this study

Scenario	Proportion of demand diversion	Introduction criteria of DRT service
Scenario	Proportion of demand diversion	$△ G T_{m i n}$	$D_{m i n}$
1	10%	26.7, 30.1, 34.7, 42.5	1, 3
2	20%		1, 2, 3, 5
3	30%		1, 2, 3, 4, 8
4	40%		1, 2, 3, 4, 6, 10
5	50%		1, 2, 3, 4, 5, 7, 13

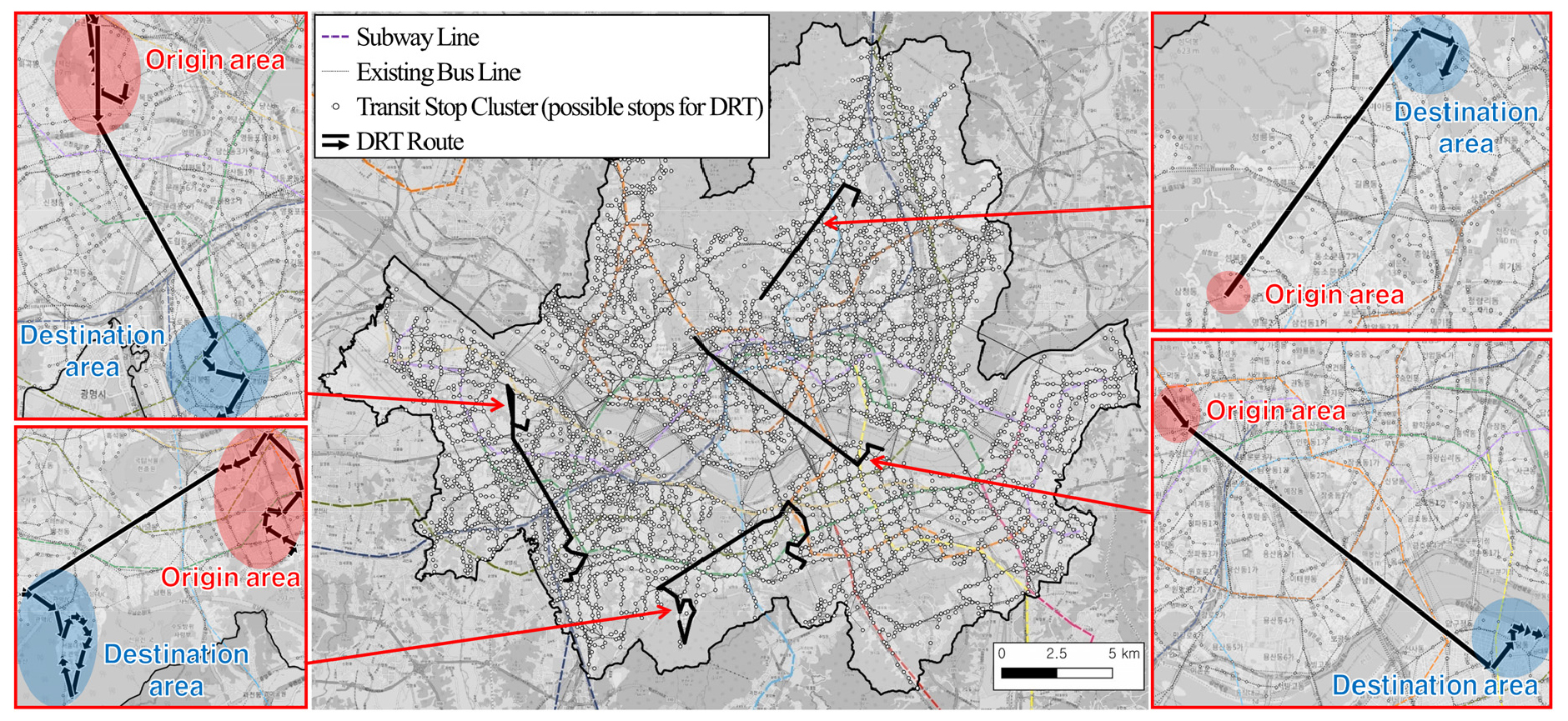
각각의 도입 기준 $(Δ G T_{m i n}, D_{m i n})$ 에 대해서 생성된 DRT 노선의 개수는 최소 1개에서 최대 270개까지, 전체 694,732개의 O-D 쌍 중 DRT가 도입되는 O-D 쌍의 개수는 최소 1개에서 7,496개까지, DRT의 수요는 최소 5인에서 최대 8,474인까지로 나타났다. Figure 3은 본 연구에서 생성된 DRT 노선의 일부 예시를 나타낸 것이며, 기점 구역과 종점 구역에서만 정차하고 그 사이는 무정차로 운행한다는 점에서 첨두 DRT의 특징을 나타낸다.

https://static.apub.kr/journalsite/sites/kst/2021-039-01/N0210390108/images/kst_39_01_08_F3.jpg

Figure 3

Examples of generated DRT routes

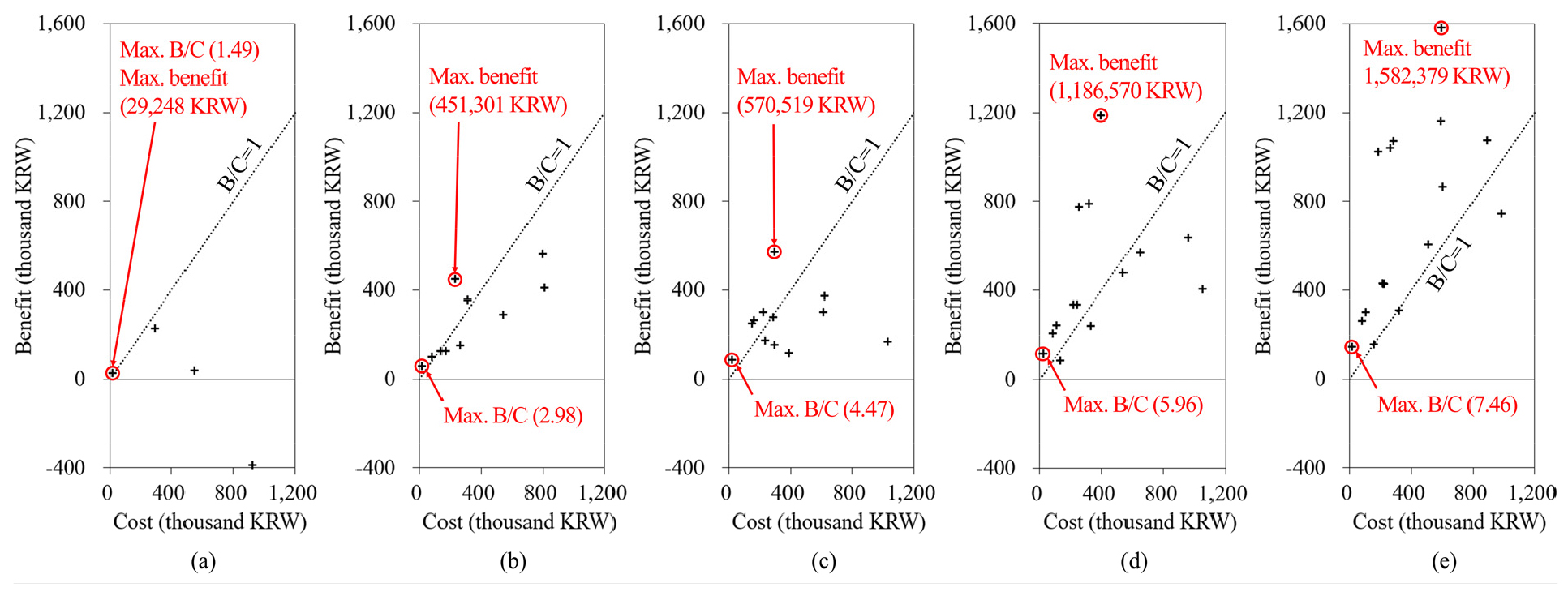
각각의 시나리오 및 DRT 도입 기준별로 비용과 편익을 평가하였으며, 이때 비용 및 편익의 분포는 Figure 4와 같다. 또한, 최적의 도입 기준을 결정한 결과는 Table 3과 같다. 예를 들어, 시나리오 5에서 B/C를 최대화하는 도입 기준은 $△ G T_{m i n}$ =26.7분, $D_{m i n}$ =13인일 때이며, 편익을 최대화하는 도입 기준은 $△ G T_{m i n}$ =42.5분, $D_{m i n}$ =2인일 때이다. 그리고 B/C를 최대화할 때 DRT 노선의 개수는 모든 시나리오에서 1개, DRT가 도입되는 O-D 쌍의 개수 역시 1개, 승객 수는 시나리오에 따라 5-25인에 불과하였다. 그러나 편익을 최대화할 때는 각각 시나리오에 따라 1-4개, 1-45개, 5-146인으로 더 높게 나타났다. 이에 따라 B/C를 최대화할 때의 편익의 크기는 29-146천 원으로, 편익을 최대화할 때의 29-1,582천 원에 비해 매우 작게 나타났다. 또한, 시나리오 5로 갈수록, 즉 대중교통에서 DRT로의 수요 전환율이 높아질수록 편익이 증가하는 것으로 나타났다.

https://static.apub.kr/journalsite/sites/kst/2021-039-01/N0210390108/images/kst_39_01_08_F4.jpg

Figure 4

Cost and benefit of DRT for different criteria in scenarios (a) Scenario 1, (b) Scenario 2, (c) Scenario 3, (d) Scenario 4, and (e) Scenario 5

Table 3.

Optimal introduction criteria of DRT service determined based on the maximization of B/C and benefit

Scenario	Demand diversion	$△ G T_{m i n}$	$D_{m i n}$	Number of DRT routes	Benefit (thousand won)	Cost (thousand won)	B/C	O-D pairs to introduce DRT	Number of DRT passengers
Maximization of B/C
1	10%	26.7	3	1	29	20	1.49	1	5
2	20%	26.7	5	1	58	20	2.98	1	10
3	30%	26.7	8	1	88	20	4.47	1	15
4	40%	26.7	10	1	117	20	5.96	1	20
5	50%	26.7	13	1	146	20	7.46	1	25
Maximization of benefit
1	10%	26.7	3	1	29	20	1.49	1	5
2	20%	42.5	2	1	451	232	1.94	9	28
3	30%	42.5	2	1	571	299	1.91	14	52
4	40%	42.5	2	2	1,187	397	2.98	21	80
5	50%	42.5	2	4	1,582	597	2.65	45	146

논의

1. DRT 서비스 도입 전략

실제로 DRT 서비스가 도입되면 대중교통에서 DRT로 전환되는 수요는 다양한 요소에 영향을 받으나, 본 연구에서는 이것을 수요 전환율에 대한 시나리오로 가정하였다. 앞서의 결과에서 대중교통으로부터 DRT로의 수요 전환율이 높아질수록 DRT 도입의 편익이 증가하는 것으로 나타났으며, 이는 실제 DRT 도입 시 대중교통으로부터의 수요 전환이 충분히 이루어지지 못한다면 DRT 도입의 경제성이 확보되지 못할 수 있음을 의미한다. 이 경우, DRT의 요금을 저렴하게 책정하거나 DRT의 서비스 품질을 향상함으로써(예: 차내시간 단축, 대기시간 단축, 환승횟수 저감, 차내혼잡 저감 등) 수요 전환을 촉진하는 것이 필요할 수 있다.

Table 3 및 Figure 4를 통해 B/C를 최대화하는 DRT 도입 기준에서 B/C가 높게 나타나는 것은 편익이 높아서가 아니라 비용이 낮아서임을 알 수 있다. 또한, 이때는 DRT를 도입하기 위한 O-D 쌍 수요의 최솟값인 $D_{m i n}$ 의 값이 크게 나타난다. 이것으로부터 B/C를 최대화하는 방법으로 DRT의 도입 기준을 결정한다면 수요가 많은 O-D 쌍에만 DRT 서비스가 제공되며, 따라서 DRT에 의해 수송되는 승객의 수와 그에 따른 편익이 작게 산출되는 것임을 알 수 있다. 반대로, B/C를 1 이상으로 유지하는 한에서 편익의 크기를 최대화하는 방법으로 DRT 도입 기준을 결정한다면, DRT 서비스는 상대적으로 수요가 적은 O-D 쌍에도 제공될 수 있으며, 따라서 DRT에 의해 수송되는 승객의 수와 그에 따른 편익이 높게 산출되는 것이다. 단순히 투자 대비 편익의 비율을 최대화하기 위해서라면 B/C를 최대화하는 기준이 유리할 수 있으나, 편익의 크기를 최대화하는 기준을 적용하면 도시 전체에 제공되는 편익의 크기뿐만 아니라 DRT에 의해 수송되는 승객의 수 역시 증가하게 된다. 이 경우 DRT 운영 주체의 수익성이 제고되는 효과도 기대할 수 있으므로, 결과적으로 편익의 크기를 최대화하는 전략이 B/C를 최대화하는 전략에 비해 B/C는 낮아지더라도 실제 운영 측면에서는 바람직하다고 할 수 있다.

앞에서는 DRT 도입으로 인한 비용과 편익을 네트워크상의 모든 DRT 노선 및 모든 이용자에 대하여 합산하였다. 이러한 방법을 네트워크 전체가 아닌 개별 DRT 노선 단위로 적용한다면 개별 노선의 비용 및 편익을 산정할 수 있다. 또한, 본 연구에서는 각각의 DRT 도입 기준에 대해 비용 및 편익을 비교한 뒤 전체 네트워크의 B/C가 최대화되거나, B/C≥1이면서 전체 네트워크의 편익이 최대화되는 기준을 채택하였다. 그러나 개별 노선에 대해서는 각각의 DRT 노선에 대해 비용 및 편익을 비교한 뒤 B/C가 가장 높거나 편익이 가장 높은 어느 한 노선만 도입하는 것보다, 여러 노선의 DRT가 도입될 수 있음을 감안하여, B/C가 높은 순서나 편익이 높은 순서에 따라 DRT 노선의 도입 우선순위를 선정하는 것이 더욱 적절하다고 할 수 있다.

2. 민감도 분석

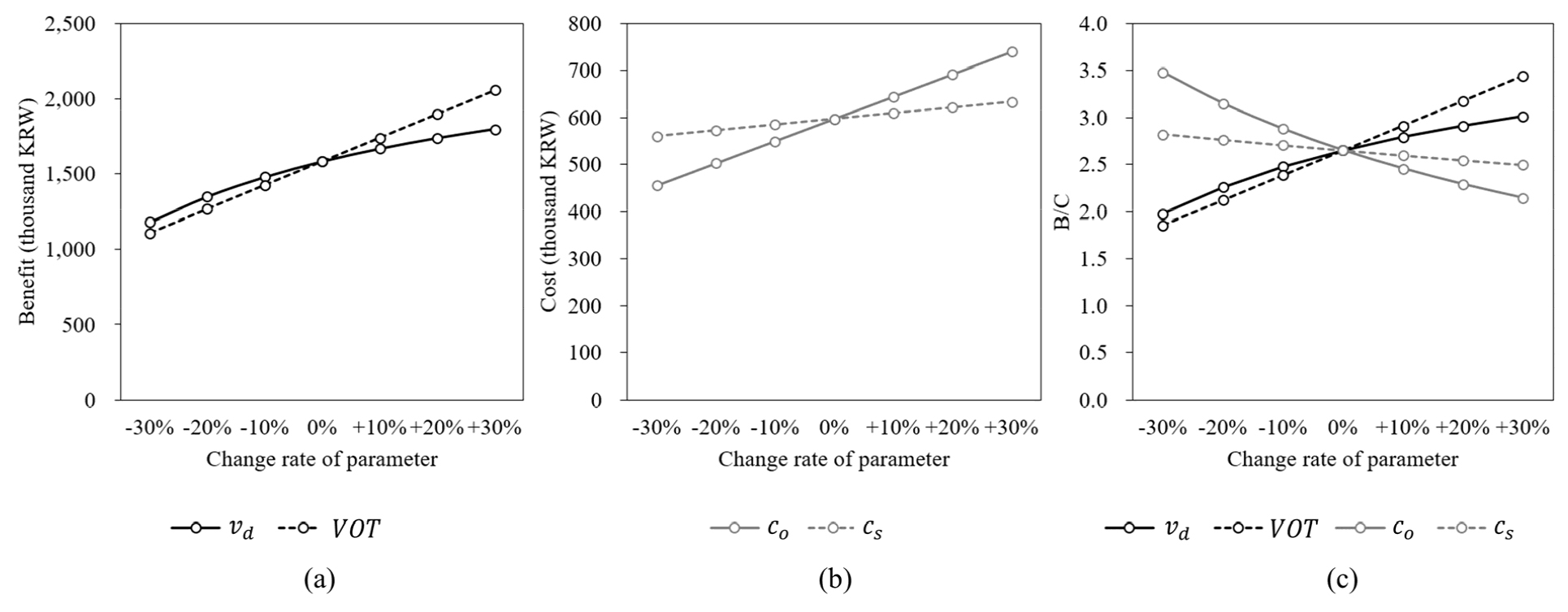
DRT의 비용과 편익은 파라미터의 값에 영향을 받는다. 본 연구에서는 DRT 차량의 속도(), 이용자의 시간가치(), 단위 거리당 운영 비용(), 단위 거리당 사회적 비용()에 대해 민감도 분석을 수행하였다. 민감도 분석은 편익이 가장 큰 시나리오 5에서 DRT의 도입 기준을 =42.5분, =2인으로 하였을 때에 대하여 시행하였으며, 각 파라미터를 -30~30% 변화시키면서 편익, 비용, B/C의 값이 어떻게 변하는지를 분석하였다. 그 결과는 Table 4 및 Figure 5와 같다.

Table 4.

Results of sensitivity analysis with respect to DRT vehicle speed ( $v_{d}$ ), value of time ( $V O T$ ), operation cost ( $c_{o}$ ) and social cost ( $c_{s}$ ) per unit distance

Changing parameter	Percentage of change in parameter
Changing parameter		-30%	-20%	-10%	0%	+10%	+20%	+30%
$v_{d}$	Benefit (won)	1,180,637	1,348,029	1,478,223	1,582,379	1,667,597	1,738,612	1,798,701
	Cost (won)	597,208	597,208	597,208	597,208	597,208	597,208	597,208
	B/C	1.98	2.26	2.48	2.65	2.79	2.91	3.01
$V O T$	Benefit (won)	1,107,665	1,265,903	1,424,141	1,582,379	1,740,617	1,898,854	2,057,092
	Cost (won)	597,208	597,208	597,208	597,208	597,208	597,208	597,208
	B/C	1.85	2.12	2.38	2.65	2.91	3.18	3.44
$c_{o}$	Benefit (won)	1,582,379	1,582,379	1,582,379	1,582,379	1,582,379	1,582,379	1,582,379
	Cost (won)	454,742	502,231	549,720	597,208	644,697	692,186	739,675
	B/C	3.48	3.15	2.88	2.65	2.45	2.29	2.14
$c_{s}$	Benefit (won)	1,582,379	1,582,379	1,582,379	1,582,379	1,582,379	1,582,379	1,582,379
	Cost (won)	560,512	572,744	584,976	597,208	609,440	621,672	633,904
	B/C	2.82	2.76	2.71	2.65	2.60	2.55	2.50

https://static.apub.kr/journalsite/sites/kst/2021-039-01/N0210390108/images/kst_39_01_08_F5.jpg

Figure 5

Benefit (a), cost (b), and B/C (c) with respect to changes in DRT vehicle speed ( $v_{d}$ ), value of time ( $V O T$ ), operation cost ( $c_{o}$ ) and social cost ( $c_{s}$ ) per unit distance

Table 4 및 Figure 5에서 볼 수 있듯이, 차량 속도 및 시간가치의 변화에 대해서는 편익의 변화가 발생하며, 운영 비용 및 사회적 비용의 변화에 대해서는 비용의 변화가 발생한다. 차량 속도와 편익의 관계는 비례하지 않으며, 차량 속도가 30% 증가하면 편익은 14% 증가하는 데 비해 차량 속도가 30% 감소하면 편익은 26% 감소하는 등, 편익은 속도가 증가할 때에 비해 감소할 때 더욱 민감하게 변동한다. 또한, 현실적으로도 교통 체증이 심한 도시의 도로망에서 DRT의 운영 속도를 높이는 것은 어렵다. 따라서 DRT 차량의 운행 속도를 높이려 하는 것보다는 DRT 차량의 운행 속도를 느려지지 않게 유지함으로써 편익을 일정 수준으로 유지하는 것이 더욱 중요함을 알 수 있다. DRT 차량이 너무 자주 정차한다면 운행 속도가 느려지므로, DRT 차량의 정류장이 너무 많아지지 않게 함으로써 운행 속도를 일정 수준 이상으로 유지하는 것이 중요하다고 할 수 있다. 한편 나머지 파라미터(시간가치, 운영 비용, 사회적 비용)과 편익 또는 비용의 관계는 비례하며, 편익은 시간가치에, 비용은 운영 비용에 특히 영향을 크게 받는다. 이로부터 실제로 DRT를 운영하고자 할 때 효과평가를 수행하고 도입 기준을 결정하고자 하는 경우에는 시간가치 및 운영 비용에 대한 정확한 추정이 보다 중요함을 알 수 있다.

결론

본 연구는 도시의 대중교통을 보완하기 위한 목적의 DRT에 대한 효과평가를 수행하였고 이를 바탕으로 DRT를 도입하기 위한 최적의 기준을 결정하였다. 이를 위해 본 연구에서는 먼저 수요가 많으면서 대중교통의 서비스 품질이 자가용에 비해 불량한 O-D 쌍을 탐색하였다. 그리고 iterative dichotomy 방법을 통해 O-D 쌍들을 공간적으로 클러스터링하였으며, 각각의 O-D 쌍 클러스터에 대해 평행 최소비용 삽입 및 타부 서치 알고리즘으로 DRT의 경로를 생성하였다. DRT 도입의 효과는 편익(이용자 비용의 감소)과 비용(운영자 및 사회적 비용)으로써 평가하였다. 이 과정을 대중교통으로부터의 수요 전환율에 대한 여러 시나리오에 대해 수행하였으며, DRT의 도입 기준(DRT를 도입하기 위한 O-D 쌍의 일반화 통행시간 차이 및 수요의 최솟값)을 변화시켜 가면서도 수행하였다.

DRT의 최적 도입 기준은 B/C의 최대화와 편익의 최대화라는 두 가지 방법으로 결정하였다. 이 중 B/C를 최대화하는 경우에는 DRT에 의해 수송되는 승객의 수와 편익이 모두 낮게 나타났으며, 편익을 최대화하는 경우에는 승객의 수와 편익이 높게 나타났다. 그러므로 DRT를 실제로 운영하는 경우에는 B/C보다 편익을 최대화하는 전략이 더욱 바람직하다. 또한, 본 연구에서는 DRT 차량의 속도, 이용자의 시간가치, 단위 거리당 운영 비용 및 사회적 비용에 대한 민감도 분석 역시 시행하였다. 그 결과 차량의 속도에 대해서는 총 편익의 크기가 차량의 속도가 높아질 때에 비해 낮아질 때 더욱 민감하게 변동하는 것으로 나타났으며, 따라서 DRT 차량의 잦은 정차는 속도의 저하를 유발하므로 지양되어야 할 것이다. 그리고 시간가치, 운영 비용, 사회적 비용에 대해서도 정확한 추정이 필요하다는 결과를 도출하였다.

본 연구에서는 이용자의 일반화 통행시간 및 이용자 비용을 산정할 때 차내시간과 환승만 고려하였으나, 향후 연구에서는 차내혼잡, 대기시간, 접근시간 등의 다른 이용자 불편 요소도 고려해야 할 것이다. 특히 본 연구에서 사용한 스마트카드 데이터에는 각 이용자의 최초 출발지점 및 최종 도착지점이 아닌 승하차 정류장만 기록되어 있으므로 스마트카드 데이터만으로는 각 이용자의 접근시간을 산출하기가 어려우며, 향후 연구에서 접근시간을 고려하기 위해서는 추가적인 데이터 또는 가정이 필요하다. 또한, 클러스터링 및 경로 생성 알고리즘도 다른 알고리즘을 적용해볼 수 있을 것이다. 그리고 본 연구에서는 DRT에 대한 공인된 수단 선택 모형이 개발되어 있지 않은 관계로 DRT가 도입되면 대중교통 수요 중 일정 비율이 DRT로 전환된다고 가정하였으며, 이에 대한 시나리오를 수립하여 분석을 수행하였다. 향후 연구에서는 DRT에 대한 수단 선택 모형을 개발하고, 아울러 DRT에 대한 수단 선택 모형을 본 연구에 적용함으로써 더욱 현실적인 DRT 도입 기준 선정 방법론을 구축하여야 할 것이다.

Funding

This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT)(No. NRF-2020R1F1A1061802).

알림

본 논문은 대한교통학회 제82회 학술발표회(2020.6.25.-26.)에서 발표된 내용을 수정 ‧ 보완하여 작성된 것입니다.

References

Beaudry A., Laporte G., Melo T., Nickel S. (2010), Dynamic Transportation of Patients in Hospitals, OR Spectr., 32, 77-107. 10.1007/s00291-008-0135-6

Chapleau L., Ferland J. A., Lapalme G., Rousseau J.-M. (1984), A Parallel Insert Method for the Capacitated Arc routing Problem, Oper. Res. Lett., 3(2), 95-99. 10.1016/0167-6377(84)90049-X

Chen X., Wang Y., Ma X. (2018), Customized Bus Line Design Model Based on Multi-Source Data, Presented in Internat. Conf. on Transp. and Devel. 2018. 10.1061/9780784481547.021

Diana M., Quadrifoglio L., Pronello C. (2009), A Methodology for Comparing Distances Traveled by Performance-equivalent Fixed-route and Demand Responsive Transit Services, Transp. Plan. and Technol., 32(4), 377-399. 10.1080/03081060903119618

Edwards D., Watkins K. (2013), Comparing Fixed-route and Demand-responsive Feeder Transit Systems in Real-world Settings, Transp. Res. Rec., 2352, 128-135. 10.3141/2352-15

Ester M., Kriegel H.-P., Sander J., Xu X. (1996), A Density-based Algorithm for Discovering Clusters in Large Spatial Databases with Noise, Proc. of the Second Internat. Conf. on Knowl. Discov. and Data Min. (KDD-96), 226-231.

Glover F. (1989), Tabu Search - Part 1, ORSA J. on Computing, 1(2), 190-206. 10.1287/ijoc.1.3.190

Glover F. (1990), Tabu Search - Part 2, ORSA J. on Computing, 2(1), 4-32. 10.1287/ijoc.2.1.4

Guo R., Guan W., Zhang W. (2018), Route Design Problem of Customized Buses: Mixed Integer Programming Model and Case Study, J. of Transp. Eng., Part A: Syst., 144(11), Article ID 04018069. 10.1061/JTEPBS.0000185

Guo R., Guan W., Zhang W., Meng F., Zhang Z.(2019), Customized Bus Routing Problem with Time Window Restrictions: Model and Case Study, Transportmetrica A: Transp. Sci., 15(2), 1804-1824. 10.1080/23249935.2019.1644566

Jeon S. (2016), 2014 Operation Cost Comparison Research of Transport Modes, 43-52. (in Korean)

Li J., Lv Y., Ma J. Ouyang Q. (2018), Methodology for Extracting Potential Customized Bus Routes Based on Bus Smart Card Data, Energies, 11, 2224-2338. 10.3390/en11092224

Li X., Quadrifoglio L. (2010), Feeder Transit Services: Choosing between Fixed and Demand Responsive Policy, Transp. Res. Part C, 18, 770-780. 10.1016/j.trc.2009.05.015

Liu T., Ceder A. (2015), Analysis of a New Public-transport-service Concept: Customized Bus in China, Transp. Pol., 39, 63-76. 10.1016/j.tranpol.2015.02.004

Lyu Y., Chow C.-Y., Lee V. C. S., Li Y., Zeng J. (2016), T2CBS: Mining Taxi Trajectories for Customized Bus Systems, Proceedings 2016 IEEE Conf. on Computer Commun. Workshops.

Lyu Y., Chow C.-Y., Lee V. C. S., Ng J. K. Y., Li Y. Zeng J. (2019), CB-Planner: A Bus Line Planning Framework for Customized Bus Systems, Transp. Res. Part C, 11, 233-253. 10.1016/j.trc.2019.02.006

Ma J., Yang Y., Guan W., Wang F., Liu T., Tu W. et al. (2017), Large-Scale Demand Driven Design of a Customized Bus Network: A Methodological Framework and Beijing Case Study, J. of Adv. Transp., 2017, Article ID 3865701. 10.1155/2017/3865701

Ministry of Land, Infrastructure and Transport (2017), Transportation Infrastructure Investment Evaluation Manual, 188. (in Korean)

Ministry of Land, Transport and Maritime Affairs (2013), Korea Highway Capacity Manual 2013, 586-609. (in Korean)

Navidi Z., Ronald N., Winter S. (2018), Comparison between Ad-hoc Demand Responsive and Conventional Transit: A Simulation Study, Pub. Transp., 10, 147-167. 10.1007/s12469-017-0173-z

Quadrifoglio L., Dessouky M. M., Ordóñez F. (2008), A Simulation Study of Demand Responsive Transit System Design, Transp. Res. Part A, 42, 718-737. 10.1016/j.tra.2008.01.018

Quadrifoglio L., Li X. (2009), A Methodology to Derive the Critical Demand Density for Designing and Operating Feeder Transit Services, Transp. Res. Part B, 43, 922-935. 10.1016/j.trb.2009.04.003

R Documentation (2019), hclust: Hierarchical Clustering, https://www.rdocumentation.org/packages/stats/versions/3.6.2/topics/hclust. (Accessed Jan 29, 2020)

Yoo G.-S. (2015), Transfer Penalty Estimation with Transit Trips from Smartcard Data in Seoul, Korea, KSCE J. of Civ. Eng., 19(4), 1108-1116. 10.1007/s12205-013-1297-6

Zheng H., Chen J., Zhang X., Yang Z. (2019), Designing a New Shuttle Service to Meet Large-Scale Instantaneous Peak Demands for Passenger Transportation in a Metropolitan Context: A Green, Low-Cost Mass Transport Option, Sustainability, 11(18), 5025-5052. 10.3390/su11185025

Journal of Korean Society of Transportation ISSN:1229-1366(Print) 2234-4217(Online) 대한교통학회지

Preview

Performance Measurement and Determination of Introduction Criteria for Peak Demand Responsive Transit Service

ABSTRACT

MAIN

Figure 1

Schematic diagram of a peak DRT service

Figure 2

Procedure of this study’s methodology

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

Table 1.

Values assigned to the parameters in this study

Table 2.

Introduction criteria of DRT service evaluated in this study

Figure 3

Examples of generated DRT routes

Figure 4

Cost and benefit of DRT for different criteria in scenarios (a) Scenario 1, (b) Scenario 2, (c) Scenario 3, (d) Scenario 4, and (e) Scenario 5

Table 3.

Optimal introduction criteria of DRT service determined based on the maximization of B/C and benefit

Table 4.

Results of sensitivity analysis with respect to DRT vehicle speed (vd), value of time (VOT), operation cost (co) and social cost (cs) per unit distance

Figure 5

Benefit (a), cost (b), and B/C (c) with respect to changes in DRT vehicle speed (vd), value of time (VOT), operation cost (co) and social cost (cs) per unit distance

References

Results of sensitivity analysis with respect to DRT vehicle speed ( $v_{d}$ ), value of time ( $V O T$ ), operation cost ( $c_{o}$ ) and social cost ( $c_{s}$ ) per unit distance

Benefit (a), cost (b), and B/C (c) with respect to changes in DRT vehicle speed ( $v_{d}$ ), value of time ( $V O T$ ), operation cost ( $c_{o}$ ) and social cost ( $c_{s}$ ) per unit distance