Signal Progression Model for Optimizing Offset Based on Secondary Band

Junsoo Jeon; Yohee Han; Youngchan Kim

doi:10.7470/jkst.2024.42.2.139

Preview

Article

Journal of Korean Society of Transportation. 30 April 2024. 139-151
https://doi.org/10.7470/jkst.2024.42.2.139

Signal Progression Model for Optimizing Offset Based on Secondary Band

이차 연동폭 기반의 옵셋 최적화 방법론 개발

Junsoo JEON¹

Yohee HAN²

Youngchan KIM³^*

전 준수¹

한 여희²

김 영찬³^*

¹Master Course, Department of Transportation Engineering, University of Seoul, Seoul 02504, Korea

²Research Professor, Department of Transportation Engineering, University of Seoul, Seoul 02504, Korea

³Professor, Department of Transportation Engineering, University of Seoul, Seoul 02504, Korea

¹서울시립대학교 교통공학과 석사과정

²서울시립대학교 교통공학과 연구교수

³서울시립대학교 교통공학과 교수

^{*Corresponding Author}

ABSTRACT

Traffic congestion costs in South Korea account for approximately 3% of the country’s GDP, and urban road congestion is estimated to exceed 1%. This congestion is primarily caused by inefficient signal control. To address this issue, various studies have been conducted to improve traffic flow through signal optimization. However, previous studies have only taken into account bandwidth, which cannot include stopped vehicles. Therefore, this study designed a signal optimization methodology that considers the travel time of all individual vehicles passing through a corridor. By introducing the concept of a secondary band, vehicles that enter outside the bandwidth are reflected. To optimize the offset in terms of extra travel time by bandwidth and the secondary band, a genetic algorithm was utilized. The effectiveness of the proposed model was evaluated by micro simulation and compared with the existing traffic signal optimization methods, SYNCHRO and PASSER in low traffic volume. The results show that the proposed model is more efficient from the perspective of a travel time of up to 3% and stopped delay at 10%. This is because it guides vehicles to pass through a signalized intersection using the bandwidth. The proposed model has a distinction of showing about 30% lower travel time variability than other methodology. In the future, this model can be applied to signal optimization at the network level, broadening its spatial applicability.

Keywords

bandwidth

extra travel time

genetic algorithm

offset

secondary band

2020년 기준 우리나라의 교통혼잡비용은 전체 GDP의 약 3%에 해당하며, 이 중 도시부 도로는 약 1% 이상으로 추정된다. 도시부 도로의 교통혼잡은 주로 비효율적인 신호제어로 인해 초래된다. 이를 해결하기 위해 차량의 이동성을 개선하기 위한 다양한 신호 연동 최적화 연구가 진행되었다. 그러나, 전체 교차로 구간에서 하나의 연동폭을 고려하는 기존의 연구는 연동폭 활용이 어려운 차량을 반영하지 못하는 한계가 있다. 이에 본 연구는 신호 교차로를 주행하는 모든 개별차량의 통행시간을 고려한 축 단위의 신호 연동 최적화 방법론을 설계하였다. 이차 연동폭 개념의 도입을 통해 최상류부 교차로 기준으로 연동폭 구간 이외 시간에 교차로에 진입한 차량을 함께 고려하였다. 연동폭과 이차 연동폭 기준의 추가통행시간을 최소화하는 옵셋을 산정하기 위하여 유전자 알고리즘을 활용하였다. 본 방법론의 효과를 평가하기 위해 낮은 교통량 상황의 시뮬레이션 환경에서 기존 신호 최적화 방법론인 SYNCHRO 및 PASSER와의 분석을 수행하였다. 분석 결과, 본 방법론은 기존 방법론에 비해 통행시간을 최대 3%, 정지지체를 약 10% 수준에서 감소시키는 효율적인 신호를 설계함을 확인하였다. 이는 차량이 진입한 신호주기 내 연동폭을 이용하여 전체 구간을 통과하도록 유도하였기 때문이다. 그 결과 제안 방법론은 기존 대비 약 30% 낮은 통행시간 편차를 보이는 차별성을 가졌다. 향후 공간적 범위를 확장하여 네트워크 단위의 신호 연동 최적화 방법론에 활용될 수 있을 것으로 기대한다.

키워드

연동폭

추가통행시간

유전자 알고리즘

옵셋

이차 연동폭

MAIN

서론
기존 문헌 고찰
이차 연동폭 기반 양방향 옵셋 최적화 방법론
1. 이차 연동폭(Secondary Band) 정의
2. 추가통행시간 산출
3. 유전자 알고리즘 기반의 최적화
시뮬레이션 분석
1. 분석환경 설정
2. 평가 지표 선정
3. 분석 결과
결론 및 향후 연구

서론

도시부 도로에서 비효율적인 신호 운영은 차량의 통행시간을 증가시켜 교통혼잡을 유발한다. 이를 개선하기 위한 여러 신호 최적화 연구들이 수행되었다. 교통혼잡비용으로 인한 경제적 손실은 우리나라에서만 2020년 기준 57.64조 원으로 추정된다(Korea Transport Institute, 2022). 특히 도시부 도로의 교통혼잡비용은 20.14조 원으로 전체의 34.9%에 해당한다. 이는 여전히 신호 최적화 연구를 통한 지체 및 통행시간 절감을 통한 도로 소통 개선의 필요성을 나타낸다.

현재까지 신호 최적화는 연동폭 최대화와 지체 최소화 같은 다양한 방법론을 통하여 진행되었다. 연동폭 기반의 연구는 연속된 교차로를 정지하지 않고 통과할 수 있는 시간대 폭인 연동폭의 크기를 최대화하여 소통을 개선하고자 하였다(Brooks, 1965; Little et al., 1981; Gartner et al., 1991). 또한 Webster(1958)와 Miller(1963)가 지체 산정 및 지체 최소화 신호 설계 방법론을 확립한 이래로 지체 최소화를 바탕으로 한 여러 연구가 수행되었다(Sun et al., 2003; Han et al., 2023).

신호 연동은 연속된 신호 교차로를 통과하는 차량의 흐름에 영향을 미친다. 따라서 잘못 설계된 연동은 차량이 경험하는 지체 및 통행시간을 악화시킨다. 이에 교차로를 주행하는 운전자가 가장 직접적으로 체감할 수 있는 신호 연동에 대한 최적화를 수행하였다. 본 연구에서는 두 개 이상의 교차로를 연속으로 통과할 수 있는 이차 연동폭이라는 새로운 개념을 도입하고 이를 기존 연동폭과 함께 고려하여 신호 운영의 효율성을 극대화하였다. 해당 방법론은 전통적인 연동폭 구간에만 국한되지 않고 연동폭 구간 이외의 상황까지 포괄적으로 고려함으로써 기존 한계를 극복하였다.

축 단위 네트워크의 공간적 범위에서 양방향 기준의 신호 연동 최적화를 수행하였다. 본 연구에서 개발된 방법론의 효과 평가를 위하여 시뮬레이션 분석을 통한 기존 최적화 방법론과 비교하였다. 제안 방법론은 평가 지표로 선정한 연동폭, 통행시간, 통행시간 편차, 정지지체의 측면에서 우수한 결과를 확인하였다. 특히 모든 분석 시나리오에서 가장 낮은 통행시간 편차를 가지는 특징을 가진다.

기존 문헌 고찰

연동폭 최대화 방법론은 PASSER-Ⅱ에 사용된 Brooks(1965)의 간선 최소화 기반의 연구로 시작되었다. Little et al.(1981)은 혼합 정수 선형 계획법을 이용하여 간선도로 연동폭 최대화 방법론인 MAXBAND 알고리즘을 설계하였다. 현재까지 MAXBAND를 기반으로 한 다양한 연구가 진행되었으며 Gartner et al.(1991)은 링크별 교통량을 바탕의 MULTIBAND를 제안하였다. Zhang et al.(2015)는 AM-BAND를 통해 MULTIBAND의 제약을 완화하여 방향별 녹색시간을 반영한 비대칭적인 연동폭을 가지는 신호를 설계하였다. 연동폭을 이용하는 상황에서 차량은 별도의 추가 지체를 경험하지 않고 해당 구간을 통과할 수 있는 특징이 있다. 그러나, 연동폭 기준의 방법론은 실제 차량의 지체를 반영하는 데 한계가 있다. 또한 교차로 수가 많거나 녹색시간이 짧은 교차로가 존재할 시 신호 설계의 어려움이 존재한다.

지체 최소화 기반의 연구는 원활한 차량의 통행을 지원하기 위해 지체를 감소하는 데 중점을 두었다. 연동폭 기반 방법론과 달리 연동폭을 고려하지 않기에 교차로 수 및 녹색시간의 길이로 인한 최적 신호 탐색에 제약이 발생하지 않는다. 지체 최소화 기반의 매크로 시뮬레이션 SYNCHRO는 지체와 정지 횟수를 최소화하는 신호를 설계한다(Cubic ITS, 2019). 연동 측면에서 SYNCHRO는 지체를 최소화는 옵셋을 산출한다. TRANSYT-7F(University of Florida McTrans Center, 2021)는 지체와 정지 횟수와 연동, 연료 소모량, 통과교통량을 반영한 신호를 설계한다. 또한 교차로 그룹을 주행하는 차량이 하류부 교차로의 녹색시간을 이용하여 연속 진행할 수 있는 기회인 PROS(Progression Opportunities)를 기준으로 최적 신호를 산출한다(Wallace et al., 1982). PROS는 특정 속도를 기준으로 주행하는 차량이 연속 통과하는 교차로 수의 합을 의미하며 이를 통해 해당 구간을 정지 없이 통과할 수 있는 신호를 설계한다.

효율적인 신호를 설계하기 위하여 여러 최적화 방법론을 활용하고 있다. 크게 선형 계획법 기반의 연구와 휴리스틱 알고리즘 기반으로 최적해를 탐색하는 연구로 구분할 수 있다. 연동폭 최대화 방법론은 양방향 연동폭을 최대화하기 위해 주로 혼합 정수 선형 계획법과 같은 선형 계획법을 이용한다. 반면 지체 최소화 방법론은 주로 휴리스틱 알고리즘을 활용한다. 신호 교차로의 옵셋 변화에 따른 지체는 선형관계를 보이지 않기 때문에 주로 휴리스틱 알고리즘을 통해 최적해를 탐색한다. TRANSYT-7F는 유전자 알고리즘과 언덕 등반 기법을 통해 최적 신호를 설계하며 이외에도 다양한 휴리스틱 알고리즘을 통한 연구가 진행되었다.

유전자 알고리즘(GA, Genetic Algorithm)은 신호 최적화를 포함한 다양한 분야에 활용되는 대표적인 휴리스틱 알고리즘이다. Foy et al.(1992)를 시작으로 유전자 알고리즘 기반의 신호 최적화 연구는 현재까지 이어지고 있다. Park(1998), Kim and Yoo(2000), Yun and Park(2012)은 유전자 알고리즘 기반의 지체를 최소화하는 신호를 설계하였다. Stevanovic et al.(2008)은 SYNCHRO의 최적 신호와 비교하여 유전자 알고리즘 기반 대중교통 우선신호의 우수성을 확인하였다. 최근에는 머신러닝을 GA와 함께 활용한 연구도 수행되었다(Mao et al., 2021).

본 연구는 이차 연동폭 기반의 연동폭 최대화 방법론을 제안하여 축 단위 네트워크에서 최적 옵셋을 산출하였다. 이를 위해 교차로 그룹을 통과하며 차량이 경험하는 적색시간의 누적 합인 추가통행시간을 최소화하는 유전자 알고리즘을 설계하였다. 기존 연동폭 기반의 연구는 교차로 그룹 전체에서 녹색신호를 받아 통과하는 연동폭을 최대화한다. 이에 연동폭을 제외한 녹색시간을 이용하는 차량에 대한 고려에 한계가 존재한다. 본 연구는 이차 연동폭 개념의 도입을 통해 연동폭을 포함한 최상류부 교차로 기준의 모든 녹색시간을 동시에 고려하는 신호를 설계하였다. 또한 본 방법론은 연동폭이 생성에 어려움이 존재하는 교차로 수 및 녹색시간의 제약 상황에서도 추가통행시간 바탕의 신호 연동 최적화가 가능하다.

이차 연동폭 기반 양방향 옵셋 최적화 방법론

1. 이차 연동폭(Secondary Band) 정의

본 연구에서 새롭게 정의한 이차 연동폭과의 구분을 위해 기존의 연동폭(Bandwidth)을 주 연동폭(Primary Band)으로 정의하였다. 이차 연동폭(Secondary Band)이란 교차로 그룹 전체가 아닌 2개 이상의 연속된 교차로를 정지하지 않고 통과할 수 있는 녹색시간 폭이다. 따라서 최상류부 교차로의 녹색시간은 주 연동폭의 녹색시간과 적색신호를 한 번이라도 경험하는 이차 연동폭에 해당하는 녹색시간으로 구분하였다.

양방향을 기준으로 모든 교차로를 연속 통과하는 주 연동폭과 한 개의 교차로 이상에서 정지를 경험하는 이차 연동폭을 함께 고려한 최적 신호를 설계하였다. 이차 연동폭을 반영한 신호 최적화는 기존 연구의 한계인 주 연동폭을 이용하지 못하는 상황에 대한 고려가 가능하다. Figure 1(a), (b)는 각각 연동폭 최대화 방법론의 대표적인 MAXBAND 및 MULTIBAND를 표현하였다. Figure 1(c)은 본 연구에서 제안한 신호 최적화 방법론의 개념을 동일한 신호 계획 상황에서 시공도 기반으로 표현하였다. MAXBAND는 양방향 연동폭 최대화, MULTIBAND는 교통량에 따른 구간별 연동폭 크기 변화, 제안 방법론은 이차 연동폭과 주 연동폭을 함께 고려하는 특징을 가진다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420202/images/kst_2024_422_139_F1.jpg

Figure 1.

Band of bandwidth maximization models

2. 추가통행시간 산출

본 연구에서는 추가통행시간(ETT, Extra Travel Time)의 개념을 정의하고 이를 최소화하는 신호를 설계하였다. 추가통행시간이란 차량이 특정 교차로 구간을 주행하며 개별 교차로에서 적색신호로 인해 대기하며 녹색신호 개시까지 발생하는 대기시간을 누적한 값이다. 다시 말해 개별차량이 해당 구간을 통행하며 경험하는 적색 시간의 누적 합을 의미한다. 교통량이 많지 않은 도로에서 통행시간은 설계속도로 물리적 길이를 주행하는 통행시간과 신호의 영향으로 추가로 경험하는 통행시간으로 구분할 수 있다. 신호로 인해 발생하는 통행시간은 차량의 정지로 인한 감속 및 가속으로 인한 시간과 신호로 인해 대기하는 시간으로 분류할 수 있다. 본 연구는 유전자 알고리즘을 설계하여 적색신호로 인해 대기하는 시간인 추가통행시간만을 대상으로 이를 최소화하는 최적 옵셋을 산출하였다.

본 연구에서는 추가통행시간을 분석하기 위해 일반적인 시공도에서 기준 속도로 주행한 시간을 제외한 시공도로 변환하였다. Figure 2(b)에서 하류부 교차로의 옵셋을 최상류부 교차로부터 주행한 시간만큼 조정하였다. 따라서, 변환 시공도에서 차량의 궤적은 적색신호로 인해 대기하여 추가통행시간이 발생한 경우에만 수평 방향으로 이동한다. 이를 통해 기준 속도로 주행하는 시간은 시공도 상에 반영되지 않는다. 이러한 변환은 시공도 기반으로 추가통행시간을 산출하는데 계산상의 이점을 가진다. 차량의 궤적을 분석할 때 차량이 경험하는 신호로 인한 대기시간만 확인할 수 있기 때문이다. 양방향 기준의 신호 최적화를 수행하기 위해 각 방향의 최상류부 교차로를 기준으로 같은 방식을 통해 시공도를 변환하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420202/images/kst_2024_422_139_F2.jpg

Figure 2.

Modified time-space diagram for proposed model

최상류부 교차로의 녹색시간을 기준으로 1초에 한 대씩 차량을 균일하게 발생하는 상황을 가정하여 각 차량이 경험하는 추가통행시간을 산출하였다. 양방향에 대해 진입하는 모든 개별차량을 고려하여 추가통행시간의 합을 최소화한다. 다만, 차량이 교차로에서 추가로 정지할지라도 추가통행시간을 최소화 기준의 옵셋을 산정한다.

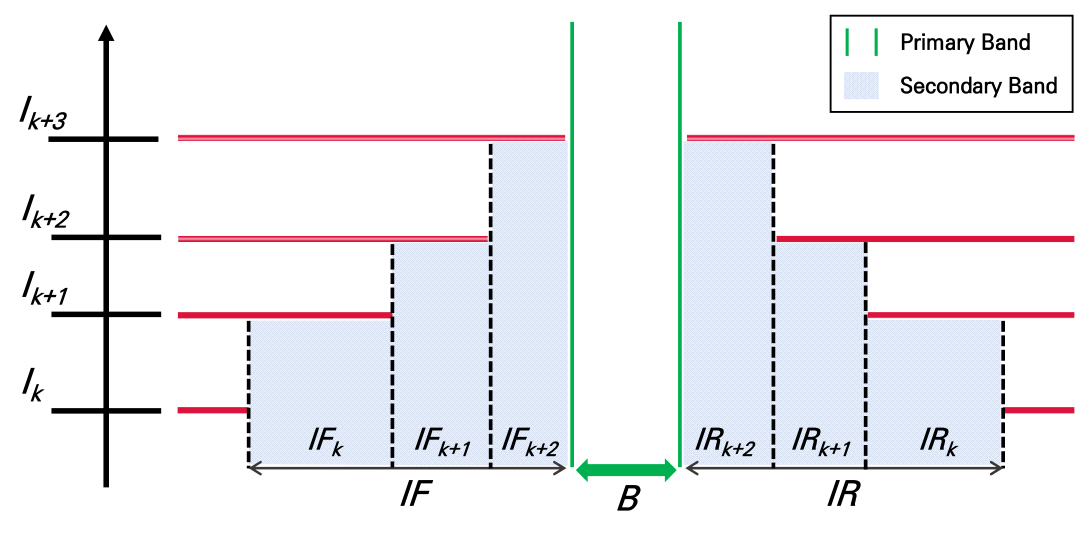
Figure 3에서 최상류부 교차로 녹색시간을 기준으로 주 연동폭과 이차 연동폭으로 나누었다. 이차 연동폭 구간은 주 연동폭 이전 녹색시간 구간인 IF(Interference Front) 구간과 주 연동폭 이후의 녹색시간 구간인 IR(Interference Rear) 구간으로 구분하였다. 추가통행시간은 주 연동폭 구간과 IF 구간, IR 구간을 기준으로 나누어 산출하며 양방향 추가통행시간을 산출한다. 구간 세분화를 통해 계산속도 측면의 유리함과 각 구간의 추가통행시간을 별도로 분석할 수 있는 이점을 가진다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420202/images/kst_2024_422_139_F3.jpg

Figure 3.

Devision into secondary band and primary band

이차 연동폭 기준의 추가통행시간 산출을 위하여 조정 녹색시간을 정의하였다. Equation 1은 IF 구간에서 상류 교차로의 녹색시간 시작 시점이 하류 교차로의 녹색시간 시점보다 이전에 존재하는 상황을 고려하였다. Equation 2를 통해 IR 구간에서 하류 교차로의 녹색시간 종점 시점이 상류 교차로의 녹색시간 종점 시점보다 이전에 존재하는 상황에서 조정 녹색시간을 정의하였다.

IR 구간의 추가통행시간은 IF 구간과 달리 다음 신호주기에 대한 고려가 필요하다. 이는 해당 구간을 주행하는 차량이 신호로 인해 정지하여 다음 신호주기의 녹색시간을 이용하여 구간을 통과하기 때문이다. 따라서 Equation 3으로 다음 주기의 녹색시간 시작 시점을 구분하여 정의하였다.

(1)

f'_{i + 1} = \{\begin{cases} f_{i + 1}, f_{i} \geq f_{i + 1} \\ f_{i}, f_{i} < f_{i + 1} \end{cases}

(2)

r'_{i + 1} = \{\begin{cases} r_{i}, r_{i} \geq r_{i + 1} \\ r_{i + 1}, r_{i} < r_{i + 1} \end{cases}

(3)

n f_{i} = f_{i} + C y c l e L e n g t h

where: f_i: start point of green time on i_th intersection

r_i: end point of green time on i_th intersection

f’_i: adjusted start point of green time on i_th intersection

r’_i: adjusted end point of green time on i_th intersection

nf_k: start point of green time on i_th intersection in next cycle length

구체적으로 이차 연동폭 구간인 IF 구간 및 IR 구간의 추가통행시간을 산출하였다. 먼저 IF 구간은 출발한 차량이 주행 및 신호로 정지하며 주 연동폭 구간까지 도달하기까지 걸린 시간이 추가통행시간으로 산정된다. IF 구간을 다시 신호 교차로 기준으로 세분화하여 i번째 교차로와 i+1번째 교차로를 통과하는 구간의 시간을 IF_i 구간으로 정의하였다. IF_i 구간의 크기는 Equation 4와 같으며 i번째 교차로의 녹색시간 시작 시점에서 i+1번째 교차로의 적색 시간 끝 시점의 길이이다. Equation 5는 IF_i 구간에 출발한 차량만을 대상으로 전체 구간을 주행하며 통과하는 개별 하류부 신호 교차로를 기준으로 분리하여 추가통행시간을 산출하였다. 따라서 $E T T_{I F_{i, j}}$ 는 IF_i 구간에서 출발한 차량이 j번째 교차로를 지나면서 경험하는 추가통행시간을 의미한다. Equation 5는 IF 구간에서 발생한 모든 차량의 추가통행시간을 합하여 IF 구간의 추가통행시간으로 산출하였다. IR 구간도 IF 구간과 동일하게 교차로 단위로 세분화하였으며 IR_i 구간의 크기는 Equation 8과 같다. Equation 9와 Equation 10으로 각 세분화 구간의 추가통행시간을 합하여 IR 구간의 추가통행시간을 산출하였다. 이는 양방향에 대해 동일한 방법론으로 적용된다.

(4)

I F_{i} = f'_{i + 1} - f'_{i}

(5)

E T T_{I F_{i, j}} = \{\begin{cases} 0, j < i + 1 \\ \frac{f'_{j -} (f'_{j - 1} - 1)}{2} \times I F_{i}, j = i + 1 \\ (f'_{j} - f'_{j - 1}) \times I F_{i}, j > i + 1 \end{cases}

(6)

E T T_{I F} = \sum_{i = 1}^{n - 1} E T T_{I F_{i}} = \sum_{i = 1}^{n - 1} \sum_{j = 1}^{n} E T T_{I F_{i, j}}

(7)

I R_{i} = r'_{i + 1} - r'_{i}

(8)

E T T_{I R_{i, j}} = \{\begin{cases} 0, j < i + 1 \\ \frac{(n f_{j} - r'_{j}) + (n f_{j} - (r'_{j - 1} - 1))}{2} \times I R_{i}, j = i + 1 \\ (f'_{j} - f'_{j - 1}) \times I R_{i}, j > i + 1 \end{cases}

(9)

E T T_{I R} = \sum_{i = 1}^{n - 1} E T T_{I R_{i}} = \sum_{i = 1}^{n - 1} \sum_{j = 1}^{n} E T T_{I R_{i, j}}

where: i: a standard intersection to subdivide IF section to IF_i subsection ( $i \leq n$ )

j: a intersection passed by vehicles departing from a specific subdivided section ( $i \leq j \leq n$ )

n: number of intersections in SA

IF_i, IR_i: a subdivided section between i_th intersection’s green time and

i+1_th intersection’s red time on IF section, IR section

ETT_IFi,j, ETT_IRi,j: sum of extra travel time on j_th intersection by vehicles departing from IF_i section, IR_i section

ETT_IFi, ETT_IRi: sum of extra travel time of vehicles departing from IF_i section, IR_i section

ETT_IF, ETT_IR: sum of extra travel time of vehicles departing from IF section, IR section

결론적으로 Equation 10, Equation 11과 같이 양방향 총 추가통행시간을 주 연동폭 구간과 IF 구간, IR 구간으로 구분하여 산출하였다. 주 연동폭 구간에서 차량은 정지하지 않기 때문에 해당 구간의 추가통행시간은 0이다.

(10)

E T T_{b o u n d_{k}} = E T T_{I F_{k}} + E T T_{B a n d_{k}} + E T T_{I R_{k}}

(11)

E T T_{a r t e r i a l} = \sum_{k = 0}^{1} E T T_{b o u n d_{k}}

where: ETT_{bound k}: sum of extra travel time on bound k

ETT_arterial: sum of total extra travel time on arterial

3. 유전자 알고리즘 기반의 최적화

휴리스틱 알고리즘 중 하나인 유전자 알고리즘을 통해 축 단위의 양방향 추가통행시간을 최소화하는 신호를 설계하였다. 본 연구는 Figure 4와 같이 유전자 알고리즘을 구성하여 신호 연동 최적화를 수행하였다. GA는 다윈의 적자생존 이론을 기본개념에서 착안한 전역해 탐색 최적화 기법이다(Holland, 1992). 이는 진화의 개념을 모방하여 세대(generation)를 거듭하며 최적해를 탐색함을 의미한다. 한 세대 내에는 여러 개의 염색체(chromosome)가 존재하며 해 집단(population)을 이룬다. 염색체 내에는 다수의 유전자(gene)가 존재하며 이를 바탕으로 미리 설정한 적합 함수(fitness function)에 따른 적합도를 산출한다. 염색체들은 적합도를 기준으로 선택(selection), 교차(crossover), 변이(mutation)의 과정을 거치며 새로운 염색체를 생성한다. 다음 세대를 형성하는 염색체 생성에 대한 다양한 방법론이 존재하며 교차와 변이는 각각의 특정 확률로 발생하게 된다. 일반적으로 초기 세대의 생성은 설정한 제약 내에서 무작위로 이루어진다. 유전 알고리즘의 전체 프로세스는 사전에 설정한 세대를 모두 지나거나, 적합도가 수렴하는 조건에서 종료되도록 설정할 수 있다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420202/images/kst_2024_422_139_F4.jpg

Figure 4.

Flow of genetic algorithm

본 연구에서 사용한 신호 최적화 유전자 알고리즘의 구현은 파이썬 라이브러리 PyGAD을 활용하였다. PyGAD은 유전자 알고리즘의 전반적인 프로세스를 사용자의 목적에 따른 설정 및 작동 과정을 추적할 수 있다(Gad, 2023). 초기 세대는 무작위로 6개의 개별 유전자가 1~100 사이의 정수를 갖도록 생성하였고 이는 6개의 개별 교차로에 할당된다. 따라서 개별 교차로의 옵셋은 각 유전자의 값을 기반으로 신호주기의 백분율에 반올림한 값을 가진다. 유전자 알고리즘의 전체적인 과정은 미리 설정한 모든 세대를 지나고 마무리되도록 종료 조건을 설정하였다.

본 연구에서 설계한 유전자 알고리즘의 적합한 파라미터를 탐색하기 위하여 후보군을 설정하고 민감도 분석을 통해 그 값을 결정하였다(Table 1). 일반적으로 세대 수와 세대 내 염색체 수의 값은 클수록 성능은 좋아지나 산출 비용이 증가하는 경향을 보인다. 이러한 특징을 고려하여 본 연구는 민감도 분석을 통해 세대 수 100, 세대 내 염색체 수 100의 조합을 사용하였다. 선택 방법론은 민감도 분석을 통해 가장 적절한 방법론이 Rank 방법론임을 확인하였다. 해당 방법론은 적합도를 기준으로 순서를 매기고 절대적인 적합도 값이 아닌 순서에 기반한 선택확률을 부여한다. Tan et al.(2017)과 Zhang et al.(2018)은 Rank 방법론 기반의 신호 최적화 연구를 수행하여 그 효과를 확인하였다.

Table 1.

Selected genetic algorithm setting for sensitivity analysis

Setting	Evaluated values	Optimal value
Combination of Generation & Population	200 & 100 100 & 100 50 & 200 200 & 50	100 & 100
Selection type	Tournament Rank Random Roulette Wheel	Rank
Crossover probability	0.4 0.5 0.6 0.7 0.8	0.8
Mutation probability	0.005 0.01 0.03 0.05	0.03

교차 및 변이 방법론으로는 uniform 교차 및 random 변이 방법론을 채택하여 사용하였다. Uniform 교차는 각 자리에 해당하는 유전자마다 두 개의 부모 염색체의 유전자를 50% 확률로 선택하여 새로운 염색체를 생성한다. Syswerda(1989)는 여러 교차 방법론 중 uniform 방법론이 가장 우수함을 확인하였다. 또한 해당 방법론은 여러 신호 최적화 연구에서 사용되었다(Benekohal and Goldberg, 1992; Park, 1998; Hajbabaie and Benekohal, 2015). 변이 방법론은 본 연구에 적합하며 여러 신호 최적화 연구에서 사용한 random 방법론을 채택하였다(Park, 1998; Yun, 2006; Varia and Dhingra, 2004). 해당 방법론은 simple random mutation 혹은 random setting mutation이라고도 불리며 본 연구는 설정한 변이 확률에 해당하는 유전자가 1~100 사이의 무작위 값을 갖도록 설계하였다. 이러한 교차 및 변이 과정을 통해 염색체의 적합도가 유사해짐을 방지하며 전역 해를 탐색하였다. 교차 및 변이 비율은 민감도 분석을 통해 각각 0.8, 0.03의 값을 사용하였다. 더하여 적합도가 우수한 일부 염색체를 다음 세대에 그대로 전달하는 elitism 방법론을 통해 우수한 개체가 손실되는 것을 방지하였다.

결론적으로 문헌 검토와 민감도 분석을 통해 Table 2에서 기술한 방법론 및 Hyper-parameter 기반으로 신호 연동 최적화 유전자 알고리즘을 설계하였다.

Table 2.

Hyper-parameter setting for genetic algorithm

Hyper-parameter	Value
Generation size	100
Population size	100
Number of genes	6
Selection type	Rank Selection
Crossover type	Uniform Crossover
Mutation type	Random Mutation
Elitism	5
Crossover probability	0.8
Mutation probability	0.03

시뮬레이션 분석

1. 분석환경 설정

양방향 축 단위 네트워크에서 제안 방법론의 효과를 평가하기 위해 경기도 고양시 덕양구 화중로의 6개 신호 교차로 축을 공간적 범위로 설정하였다(Figure 5(a)). Figure 5(b)와 같이 임의로 설정한 v/c 0.3 수준의 낮은 교통량 상황에서의 시뮬레이션 환경을 구축하였다. 해당 구간을 통행하는 차량의 속도는 40km/h로 설정하였다. 교통량이 동일한 상황에서 신호주기만을 구분하여 80초, 100초, 120초, 140초, 160초의 5가지 시나리오에서 분석을 수행하였다. 다양한 신호주기 상황에서의 최적 신호 설계를 통해 제안 방법론의 범용성을 확인하고자 하였다. 분석 시 녹색신호 비율과 현시 순서는 현황 TOD를 바탕으로 설정하였다. Figure 6의 개요도와 같이 분석 환경 및 시나리오 구축, 개별 방법론을 통한 최적 옵셋 산출, 이를 바탕으로 시뮬레이션 분석을 수행하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420202/images/kst_2024_422_139_F5.jpg

Figure 5.

Test site : Hwajeong-ro, Goyang-si, Korea

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420202/images/kst_2024_422_139_F6.jpg

Figure 6.

Overview of research methodology

2. 평가 지표 선정

축 단위 네트워크에서의 산출된 최적화 옵셋을 효과를 분석하기 위하여 Table 3의 4가지 평가 지표를 선정하였다. 먼저 양방향 연동폭 크기를 비교하여 제안 방법론이 이차 연동폭을 고려하며 동시에 연동폭 최대화를 수행함을 확인하고자 하였다. 또한 양방향 축 기준의 평균 정지지체와 평균 통행시간을 기준으로 지체 측면에서 신호 설계를 평가하였다. 통행시간의 표준편차를 함께 비교하여 동일 구간을 주행하는 차량의 통행시간 변동성을 확인하였다. 마지막으로 축 단위 분석 구간에서 신호 및 교통량의 영향으로 발생하는 차량의 정지를 차량당 평균 정지 횟수를 통해 비교하였다.

Table 3.

Selection of measurement of effectiveness

Measurement of effectiveness	Definition
Bandwidths	Two-way bandwidths
Average travel time	Free flow travel time plus travel time delay
Average travel time standard deviation	The variability of travel time
Average stopped delay	Stopped time caused by traffic signal control
Average number of stops	Number of stops by traffic signal control and adjacent vehicles

3. 분석 결과

Figure 7은 5개 신호주기 시나리오 상황에서 본 연구의 제안 방법론과 SYNCHRO, PASSER 방법론의 최적 신호를 바탕으로 수행한 시뮬레이션 분석 결과이다. 순서대로 주 연동폭 크기, 통행시간 및 통행시간 편차, 정지지체, 차량당 정지 횟수를 기준으로 각 방법론의 효과를 비교한 그래프이다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420202/images/kst_2024_422_139_F7.jpg

Figure 7.

Comparison of results across models by cycle length

먼저, Figure 7(a)을 통해 제안 방법론이 연동폭 측면에서 다양한 신호주기 환경에 대해 효율적인 신호를 설계함을 확인하였다. 5개 중 4개의 시나리오에서 양방향 주 연동폭의 합이 대표적인 연동폭 최대화를 수행하는 PASSER 방법론과 같은 값으로 가장 컸다. 이를 통해 제안 방법론이 이차 연동폭과 주 연동폭을 함께 고려함에도 기존의 연동폭 기반의 방법론과 유사한 수준의 주 연동폭을 생성함을 보였다. 다만 신호주기 100초 시나리오 상황에서 제안 방법론은 다른 방법론에 비해 작은 주 연동폭을 가졌다. 이는 제안 방법론의 신호 최적화 과정에서 추가 통행시간의 최소화를 달성하기 위해 IR 구간을 배제한 신호를 설계하였기 때문이다. 대부분 IR 구간을 최소화함으로써 효율적인 신호를 설계할 수 있으나, 특정 상황에서는 짧은 IR 구간을 포함하는 신호 계획이 더욱 효율적일 수 있다고 판단된다.

양방향 기준 주방향 직진 이동류의 통행시간과 통행시간 표준편차를 평가 지표로 효과를 분석하였다. Figure 7(b)를 통해 제안 방법론이 대부분의 신호주기에서 가장 우수한 통행시간을 가졌다. 다만 연동폭 분석과 마찬가지로 100초 시나리오에서 IF 구간 중심의 신호 설계로 인하여 상대적으로 긴 통행시간을 보였다. 한편, Figure 7(b)의 오차막대와 그 값을 보여주는 Table 4에서 제안 방법론이 모든 시나리오에 걸쳐 기존 대비 약 30% 수준의 가장 낮은 통행시간 편차를 나타냈다. 이는 제안 방법론이 IF 구간과 주 연동폭을 중심으로 신호를 설계하였기 때문이다. IF 구간에 진입한 차량은 한 번 이상 정지할 수 있으나 해당 주기의 주 연동폭을 이용하여 전체 구간을 통과한다. 반면 IR 구간에 진입한 차량은 다음 신호주기의 녹색시간까지 정지하며 통행시간이 증가하고 이로써 편차가 증가한다. 이러한 이유로 SYNCHRO 및 PASSER 방법론 기반의 최적 신호는 제안 방법론 대비 높은 통행시간 편차를 보이게 된다.

Table 4.

Travel time standard deviation across models by cycle length

Cycle length (s)	Model
Cycle length (s)	Proposed model (s)	SYNCHRO (s)	PASSER (s)
160	25.0	30.2	38.3
140	19.5	29.2	25.1
120	21.2	24.6	24.5
100	16.3	22.7	20.9
80	16.3	18.8	22.7

마지막으로 평균 정지지체와 차량당 정지 횟수를 양방향 기준 주방향 직진 이동류를 기준으로 비교하였다. 본 연구는 VISSIM 시뮬레이션의 정지 판단 기준과 같이 0 이상의 속도로 주행하다 속도가 0이 되는 차량을 정지하였다고 판단하였다(PTV AG, 2020). Figure 7(c)에서 제안 방법론은 대부분 시나리오 상황에서 가장 작은 정지지체를 가지며 통행시간 분석 결과와 유사한 경향성을 보이며 효율적인 신호를 설계함을 확인하였다. Figure 7(d)에서 제안 방법론은 대부분 시나리오에서 가장 많은 정지 횟수를 가진다. 이는 추가적인 정지가 발생하더라도 추가통행시간을 최소화하기 위해 IF 구간에 치중된 신호를 설계하기 때문으로 판단된다. 향후 다중 목적함수 설계 통해 기존의 추가통행시간 최소화와 함께 정지 횟수 최소화를 반영하여 이러한 문제를 개선할 수 있을 것이다.

결론 및 향후 연구

본 연구는 이차 연동폭 개념을 통하여 축 단위 신호 교차로 구간에서 양방향 연동폭 최대화 방법론을 하였다. 기존의 주 연동폭과 함께 이차 연동폭을 고려한 신호 연동 최적화를 수행하여 주 연동폭을 이용하는 차량과 이용하지 못하는 차량을 함께 고려하였다. 이를 위해 차량이 교차로 그룹을 주행하며 경험하는 적색시간의 누적 합인 추가통행시간을 최소화를 목적함수로 설정하였다. 휴리스틱 알고리즘인 유전자 알고리즘을 통하여 최적 옵셋 조합을 산정하고 이를 마이크로 시뮬레이션 상황에서 타 최적화 방법론과 비교 분석하였다.

민감도 분석 및 선행연구 분석을 통하여 본 연구에 적합한 유전자 알고리즘을 설계하였다. 순위 기반 선택, 균일 교차, 무작위 변이 방법론을 통해 세대를 거듭하며 최적해를 탐색하였다. 6개 신호 교차로의 공간적 범위 및 동일 교통량 상황에서 신호주기를 다르게 설정한 5가지 분석 시나리오를 설정하였다. 이를 바탕으로 제안 방법론과 SYNCHRO, PASSER에서 산출한 최적 신호를 시뮬레이션을 기반으로 비교하였다. 연동폭 크기, 양방향 평균 통행시간 및 편차, 평균 정지지체와 차량당 정지 횟수를 평가 지표로 선정하여 설계한 신호를 평가하였다. 분석 결과 제안 방법론은 기존 연동폭 기반 방법론 수준의 연동폭 크기를 가진 신호를 설계하여 연동폭과 이차 연동폭을 동시에 고려함을 확인하였다. 통행시간 및 지체 관점에서도 우수한 결과를 보였다. 특히 가장 낮은 통행시간 편차를 가지는 특성을 확인하였으며 이는 추가통행시간을 최소화하고자 IR 구간을 배제한 신호를 설계하기 때문이다. 이러한 특성을 가진 신호 설계는 향후 군집 기반의 차량 주행 상황의 신호제어에 효과적으로 활용할 수 있다. 나아가 교통정보 제공 측면에서 신뢰도 높은 통행시간을 보장할 수 있을 것이라 기대한다. 반면 타 방법론 대비 많은 정지 횟수를 보였다. 이는 추가적인 정지를 감수하고 IF 구간 바탕의 신호를 통한 추가통행시간 최소화를 목표하였기 때문이다. 향후 현재의 추가통행시간 최소화와 함께 정지 횟수를 다중 목적함수로 설정하여 이를 고려할 수 있을 것이다. 동시에 특정 시나리오에서 발생하는 IF 구간 중심의 신호 설계로 인한 비효율성을 개선할 수 있을 것으로 기대한다.

본 연구는 최상류부 교차로를 기준으로 처음부터 전체 구간을 통과하는 차량을 고려한 이차 연동폭 기준의 신호를 설계하였다. 추가통행시간을 최소화하는 본 방법론은 정지로 인한 감가속 및 교통량으로 인해 발생하는 지체의 반영에 한계가 존재한다. 또한 낮은 교통량 상황에서 분석을 수행하였기에 다양한 교통량 상황에서 본 방법론의 효과를 확인하기 위해 추가적인 분석이 필요하다. 향후 중간 유출입 교통류에 대한 추가적인 고려를 통해 이차 연동폭의 개념을 확장하고 보다 현실적인 행태를 반영할 수 있을 것이다. 또한 균일 분포 바탕으로 차량이 진입하는 상황을 가정하였으나 분석하는 교통류 상황에 적합한 분포를 적용할 필요가 있다. 나아가 공간적 범위를 네트워크 단위로 확장하여 본 신호 최적화 방법론의 범용성에 대한 효과 검증이 필요하다.

Funding

This work was supported by the 2023 sabbatical year research grant of the University of Seoul.

알림

본 논문은 대한교통학회 제89회 학술발표회(2023.10.11.)에서 발표된 내용을 수정·보완하여 작성된 것입니다.

References

Benekohal R. F., Goldberg D. E. (1992), Signal Timing Determination using Genetic Algorithms, Transportation Research Record, (1365), 108.

Brooks W. D. (1965), Vehicular Traffic Control: Designing Traffic Progression Using a Digital Compute, Kingston, NY: IBM Data Processing Division.

Cubic ITS (2019), Synchro Studio 11 User Guide.

Foy M. D., Benekohal R. F., Goldberg D. E. (1992), Signal Timing Determination using Genetic Algorithms, Transportation Research Record, (1365), 108.

Gad A. F. (2023), Pygad: An Intuitive Genetic Algorithm Python Library, Multimedia Tools and Applications, 1-14.

10.1007/s11042-023-17167-y

Gartner N. H., Assmann S. F., Lasaga F., Hou D. L. (1991), A Multi-band Approach to Arterial Traffic Signal Optimization, Transportation Res, 25B 55-74.

10.1016/0191-2615(91)90013-9

Hajbabaie A., Benekohal, R. F. (2015), A Program for Simultaneous Network Signal Timing Optimization and Traffic Assignment, IEEE Transactions on Intelligent Transportation Systems, 16(5), 2573-2586.

10.1109/TITS.2015.2413360

Han Y., Lee H., Kim Y. (2023), Extensible Prototype Learning for Real‐time Traffic Signal Control, Computer‐Aided Civil and Infrastructure Engineering, 38(9), 1181-1198.

10.1111/mice.12955

Holland J. H. (1992), Genetic algorithms, Scientific American, 267(1), 66-73.

10.1038/scientificamerican0792-66

Kim Y. C., Yoo C. S. (2000), Development of Optimization Model for Traffic Signal Timing in Grid Networks, J. Korean Soc. Transp., 18(1), Korean Society of Transportation, 87-97.

Korea Transport Institute (2022), Estimation for Road Traffic Congestion Costs in 2020, 59-65.

Little J., Kelson M., Gartner N. H. (1981), MAXBAND: A Versatile Program for Setting Signals on Arteries and Triangular Networks, Transportation Research Record, 795 40-46.

Mao T., Mihaita A., Chen F., Vu H. (2021), Boosted Genetic Algorithm Using Machine Learning for Traffic Control Optimization, IEEE.

10.1109/TITS.2021.3066958

Miller A. J. (1963), Settings for Fixed-cycle Traffic Signals, Journal of the Operational Research Society, 14(4), 373-386.

10.1057/jors.1963.61

Park B. (1998), Development of Genetic Algorithm-based Signal Optimization Program for Oversaturated Intersections, Texas A&M University.

PTV AG (2020), PTV Vissim 2020 User Manual.

Stevanovic J., Stevanovic A., Martin P. T., Bauer T. (2008), Stochastic Optimization of Traffic Control and Transit Priority Settings in VISSIM, Transportation Research Part C: Emerging Technologies, 16(3), 332-349.

10.1016/j.trc.2008.01.002

Sun D., Benekohal R. F., Waller S. T. (2003), Multi-objective Traffic Signal Timing Optimization using Non-dominated Sorting Genetic Algorithm, IEEE IV2003 Intelligent Vehicles Symposium, Proceedings (Cat. No.03TH8683), 198-203, IEEE.

10.1007/3-540-45110-2_143

Syswerda G. (1989), Uniform Crossover in Genetic Algorithms, In ICGA, 3, 2-9.

Tan M. K. et al. (2017), Optimization of Traffic Network Signal Timing using Decentralized Genetic Algorithm, 2017 IEEE 2nd International Conference on Automatic Control and Intelligent Systems (I2CACIS), IEEE.

10.1109/I2CACIS.2017.8239034

University of Florida McTrans Center (2021), Traffic Network Study Tool: TRANSYT-7F User Guide.

Varia H. R., Dhingra S. L. (2004), Dynamic Optimal Traffic Assignment and Signal Time Optimization using Genetic Algorithms, Computer‐Aided Civil and Infrastructure Engineering, 19(4), 260-273.

10.1111/j.1467-8667.2004.00353.x

Wallace C. E., Courage K. G. (1982), Arterial Progression-New Design Approach, Transportation Research Record, 881, 53-59.

Webster F. V. (1958), Traffic Signal Settings, No.39.

10.5962/bhl.part.19110

Yun I. (2006), Stochastic Optimization Method for Coordinated Actuated Signal Systems, University of Virginia.

Yun I., Park B. (2012), Stochastic Optimization for Coordinated Actuated Traffic Signal Systems, Journal of Transportation Engineering, 138(7), 819-829.

10.1061/(ASCE)TE.1943-5436.0000384

Zhang C., Xie Y., Gartner N. H., Stamatiadis C., Arsava T. (2015), AM-Band: An Asymmetrical Multi-Band Model for Arterial Traffic Signal Coordination, Transportation Research Part C 58, 515-531.

10.1016/j.trc.2015.04.014

Zhang L., Alharbe N. R., Luo G., Yao Z., Li Y. (2018), A Hybrid Forecasting Framework Based on Support Vector Regression with a Modified Genetic Algorithm and a Random Forest for Traffic Flow Prediction, Tsinghua Science and Technology, 23(4), 479-492.

10.26599/TST.2018.9010045

Journal of Korean Society of TransportationISSN:1229-1366(Print) 2234-4217(Online)대한교통학회

Preview

Signal Progression Model for Optimizing Offset Based on Secondary Band

ABSTRACT

MAIN

Figure 1.

Band of bandwidth maximization models

Figure 2.

Modified time-space diagram for proposed model

Figure 3.

Devision into secondary band and primary band

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Figure 4.

Flow of genetic algorithm

Table 1.

Selected genetic algorithm setting for sensitivity analysis

Table 2.

Hyper-parameter setting for genetic algorithm

Figure 5.

Test site : Hwajeong-ro, Goyang-si, Korea

Figure 6.

Overview of research methodology

Table 3.

Selection of measurement of effectiveness

Figure 7.

Comparison of results across models by cycle length

Table 4.

Travel time standard deviation across models by cycle length

Funding

알림

References