Recurrent Congestion Severity Priority Analysis Methodology Based On Mobility Big-Data

Soongbong Lee; Jeongmin Kim; Seunghoon Cheon

doi:10.7470/jkst.2021.39.2.164

Preview

Article

Journal of Korean Society of Transportation. 30 April 2021. 164-176
https://doi.org/10.7470/jkst.2021.39.2.164

Recurrent Congestion Severity Priority Analysis Methodology Based On Mobility Big-Data

모빌리티 빅데이터 기반 도로부문 반복혼잡 심각도 우선순위 분석방법

Soongbong LEE¹

Jeongmin KIM²

Seunghoon CHEON³^*

이 숭봉¹

김 정민²

천 승훈³^*

¹Post-Doc Researcher, Department of National Transport Big Data, The Korea Transport Institute, Sejong 30147, Korea

²Transportation Scientist, Gyeonggi Public Investment Management Center, Gyeonggi 16467, Korea

³Research Fellow, Department of National Transport Big Data, Sejong 30147, Korea

¹한국교통연구원 교통빅데이터연구팀 박사후연구원

²경기연구원 공공투자관리센터 투자분석원

³한국교통연구원 교통빅데이터연구팀 연구위원

^{*Corresponding Author}

ABSTRACT

In order to analyze the causes of traffic congestion and prepare solutions, studies using mobility data are being actively conducted. Mobility data can manage ITS infrastructure and overcome the limitations of spatial range. In addition, it is possible to collect the trajectory of individual vehicles, enabling objective and consistent traffic monitoring and analysis across the country. The problem of traffic congestion in the road section is an important constraint affecting the development of the national economy. Therefore, assessing the level of traffic congestion on a section of the road is important for traffic management and control. In the previous studies, most of the indicators for congestion section used a single evaluation indicator. However, considering the complexity and dynamics of transportation, an evaluation method using various indicators can be effective. In this study, speed-based indicators (congestion intensity, congestion duration, congestion length, bottleneck rate, congestion rate) were set as congestion indicators in consideration of the possibility of data collection and general use. The priority of recurrent congestion severity was evaluated by calculating the composite score using various congestion indicators. Through this study, it is expected that it will be able to help prepare various measures to improve congestion, such as monitoring recurrent congestion sections, support for decision-making on transportation policies, investment in road infrastructure, and pre-post evaluation of policies.

Keywords

composite-score

congestion-index

mobility bigdata

recurrent-congestion

standardization

교통혼잡 원인 분석 및 해결방안 마련을 위해 모빌리티 데이터를 활용한 연구들이 활발하게 이루어지고 있다. 모빌리티 데이터는 ITS 인프라 관리 및 제한된 공간적 범위의 한계 극복이 가능하다. 또한, 개별차량의 주행궤적 수집이 가능하여 전국에 대해 객관적이고 일관성 있는 교통 모니터링 및 분석을 가능하게 한다. 도로구간의 교통혼잡 문제는 국가 경제발전에 영향을 미치는 중요한 제약요소이다. 따라서 도로구간의 교통혼잡 수준을 평가하는 것은 교통관리 및 제어를 위해 중요하다. 기존연구에서 혼잡구간 판단지표는 대부분 단일 평가지표를 활용하였다. 하지만 교통의 복잡성 및 역동성을 고려할 때 다양한 지표를 활용한 평가 방법이 효율적일 수 있다. 본 연구에서는 데이터 수집 가능성과 범용적인 활용을 고려하여 속도기반 지표(혼잡강도, 혼잡지속시간, 혼잡구간길이, 병목발생비율, 반복혼잡비율)를 혼잡지표로 설정하였고, 종합점수를 산정하여 우선순위를 평가하였다. 이를 통해 반복혼잡 구간 모니터링, 교통정책 의사결정 지원, 도로 인프라 투자, 정책에 대한 사전 ‧ 사후 평가 등 다양한 혼잡개선대책 마련에 도움을 줄 수 있을 것으로 기대한다.

키워드

종합점수

혼잡지표

모빌리티 빅데이터

반복혼잡

표준화

MAIN

서론
선행연구 고찰
분석방법론
1. 분석개요
2. 데이터 구축
3. 교통혼잡 지표 개발
4. 반복혼잡 우선순위 평가방법(종합점수)
분석결과
결론

서론

최근 사회경제의 급격한 발전으로 자동차 대수가 크게 증가하였지만, 제한적인 도로자원으로 교통혼잡(traffic congestion)은 증가하고 있다. 이로 인해 도로 이용자들의 안락함과 여행 편의성이 크게 떨어지고 있다. 교통혼잡 문제는 사회에 대한 광범위한 관심을 불러일으키고 있으며, 국가 경제발전에 영향을 미치는 중요한 제약요소가 되고 있다. 이러한 도로구간의 교통혼잡은 과도한 교통수요, 도로 기하구조, 교통사고 등 다양한 원인에 의해서 발생한다. 교통혼잡은 발생하는 빈도 및 원인에 따라 반복 혼잡(recurring congestion)과 비반복 혼잡(nonrecurring congestion)으로 구분할 수 있다. 반복적 혼잡은 하루 중 특정 시간대 혹은 특정구간에서 도로를 이용하는 교통량이 증가하여 발생하는 예측 가능한 혼잡을 의미한다. 반면 비반복적 혼잡은 돌발상황(교통사고, 악천후 등)과 같은 일시적으로 계획하지 않은 상황에 의해 발생하는 예측하기 어려운 혼잡을 의미한다. FHWA(2016)에 따르면 미국 혼잡구간의 약 40%는 반복적으로 혼잡이 나타나는 것으로 확인되고 있으며, 적절한 처리가 이루어지지 않으면 시간 및 비용손실이 지속적으로 증가할 수 있다고 제시하고 있다. 따라서 반복적으로 발생하는 혼잡구간의 차량을 분산시키기 위한 인프라 투자와 교통관리대책 마련이 중요하다.

교통관리 및 제어를 위해 도로구간(혼잡구간 위치 및 시간정보 등)의 교통혼잡 수준을 객관적으로 평가하는 것은 필수적이다. 하지만, 현재 교통상황을 평가하기 위한 통일되고 고정된 평가방법은 존재하지 않으며, 실제로 지역마다 다양한 평가방법이 적용되고 있다(He et al., 2016). 교통혼잡을 판단한 연구들을 살펴보면 통행속도/시간/밀도 등을 기반으로 한 단일 혼잡지표를 개발하여 평가한 연구가 다수 수행되었다. 그러나 교통의 복잡성 및 역동성 등을 고려할 때 단일 혼잡지표로 도로망의 교통 혼잡상황을 종합적으로 평가하는 것은 매우 어려운 문제다. 결과적으로 다수의 연구에서 다양한 지표를 융합하여 교통상황을 평가하기 시작하였다. 교통운영 개선의 투자를 정당화하기 위해서는 과학적이고 정확한 혼잡측정방법이 필요하다(Hale et al., 2016a). 한정된 예산으로 혼잡구간 개선효과를 극대화하기 위해서는 정확한 혼잡위치를 식별하고 순위를 정하는 것은 중요한 첫 단계이기 때문이다(Elhenawy et al., 2015).

이러한 중요성에도 불구하고 전국 도로구간을 대상으로 반복혼잡구간을 정량적으로 평가하는 것은 쉬운 일이 아니다. 국내 ITS(Intelligent Transportation System)가 도입된 이후 교통류 변수(교통량, 속도, 밀도 등) 모니터링을 위해 도로 내 및 도로 위의 센서(sensor) 기술을 기반으로 다양한 차량검지기가 개발되었다. 하지만, 기존 ITS 검지기(루프검지기, 레이더 등)는 공간적 범위가 고정된 지점 또는 구간으로 한정되어 해당구간의 실시간 모니터링을 위한 장치로 주로 활용되었다. 이로 인해 기존 ITS 검지기를 활용하여 전국에 대한 혼잡상황을 모니터링하기 위해서는 방대한 예산이 필요하다. 또한 상대적으로 혼잡한 구간을 정량적으로 판단하기 위해서 전국 도로구간을 동일한 기준으로 판단할 수 있는 것이 무엇보다 중요하다. 이러한 ITS 인프라의 공간적인 한계를 극복하기 위하여 진보된 데이터(GPS)를 활용한 연구들이 최근 들어 다수 보고되고 있다.

본 연구에서는 개별차량 위치 좌표(포인트 궤적)를 전처리 및 공간정보 상에 맵매칭하여 전국 도로구간에 대한 통행속도 자료를 구축하고자 한다. 혼잡구간 판단은 기존연구에서 제안된 지표들을 검토하여, 통행속도 기반의 혼잡지표들을 선정하였다. 마지막으로, 반복혼잡구간의 종합적인 평가를 위해, 다양한 혼잡지표를 활용하여 혼잡 심각 수준을 평가하는 반복혼잡 우선순위 산정 방법론을 제안하였다.

선행연구 고찰

교통혼잡이란 도로용량을 초과하는 교통수요나 도로 구조상의 문제, 그리고 교통사고 등 다양한 원인에 의해서 발생하는 차량의 지정체 및 대기행렬 현상을 말하며, 정상적인 자유류(free flow)의 통행상태에서 소요되는 통행시간과 비교했을 때 통행시간 또는 지체의 증가로 볼 수 있다(Lomax, 1997). 교통혼잡의 주요 발생원인은 병목현상(bottleneck), 교통사고, 날씨, 공사, 부적절한 신호, 행사 등이 있다. 일반적으로 도로에서 발생하는 교통혼잡은 반복적으로 발생하는 혼잡과 비반복적으로 발생하는 혼잡으로 구분된다. 반복적인 혼잡의 주요 원인은 과도한 수요와 병목현상인데, 병목현상은 설비의 용량이 갑자기 줄어드는 위치에서 차량의 진입, 진출로 인해 발생하는 경우가 많다(Stopher, 2004).

국내에서는 도시별 ‧ 도로관리 기관별로 ITS가 구축됨에 따라 본격적으로 도로구간의 통행속도/교통량/밀도 등을 측정할 수 있게 되었으며, 한국도로공사 등 여러 공공기관에서는 도로등급별 속도 기준값에 따라 원활, 서행, 지체로 구분한 교통혼잡 정보를 제공하고 있다. 교통상황에 대한 정확한 분류와 식별은 도로 시스템의 혼잡완화를 위한 효과적인 전략을 개발하는데 필수적이다(Kidando et al., 2017). 병목현상은 성장하고, 소멸되고, 병합되는 등의 동적특성을 지닌다(Lund et al., 2017). 또한, 병목현상은 교통간섭(traffic interruption), 차로감소(lane reduction), 합류(merging), 분류(distraction) 등 다양한 원인에 의해서 발생한다(Thakur and Singh, 2016). 이로 인해 고정적인 검지기 설치 위치를 기준으로 지점 또는 구간속도를 측정하는 기존 ITS 검지체계로는 혼잡상황의 변화를 파악하기에는 한계가 있다. 이러한 이유로 미국 등 해외 국가들에서는 HERE, INRIX, TomTom과 같은 민간 회사에서 수집된 개별차량의 위치정보 데이터를 기반으로 혼잡의 근본원인과 실제 병목지점을 식별하고, 다양한 혼잡 및 병목현상을 구성요소를 추적하기 위한 알고리즘을 개발하고 있다(Lund et al., 2017). 지금까지 국내에서는 개인정보보호법 등으로 인해서 개별차량 위치 정보를 활용하기 쉽지 않았고, 이로 인해 혼잡 식별과 관련된 알고리즘 개발이 더딘 실정이었다. 따라서 데이터 기반의 혼잡관리 정책을 수립하는 것이 쉽지 않았지만, 최근 데이터 3법 개정, 마이데이터 사업 등으로 국내에서도 가명정보 처리된 위치 정보를 연구 등 목적으로 활용할 수 있는 기반이 마련되었다.

해외에서 기 개발된 여러 혼잡판단 알고리즘을 살펴보면 다음과 같다. He et al.(2016)은 베이징 교통관리국에서 수집된 구간속도자료를 바탕으로 속도성능지수(speed performance index)를 산출하여 기존 도로망의 혼잡상태를 평가한 후 도시 도로구간과 네트워크의 혼잡도를 측정하는 방법론을 개발하였다. Hale et al.(2016a)은 45mi/h를 혼잡 임계속도로 설정하여 혼잡 지속시간, 혼잡구간 길이, 혼잡발생 일자를 확인하고, 이를 종합하여 실제 병목현상의 순위를 매겨 새로운 대책의 영향을 입증하는 소프트웨어를 개발하였다. Kidando et al.(2017)는 교통상황별 속도분포를 확인하여 임계속도를 추정하고, 교통 점유율을 지표로 교통상태를 자유흐름, 과도 흐름(혼잡시작), 정체 상태로 일반화된 선형모형을 개발하였다. Sisiopiku and Rostami-Hosuri(2017)는 미국 전역에서 수집되는 평균 통행시간 데이터(National Performance Management Research Data Set, NPMRDS)를 기반으로 도로구간의 통행시간지수(Travel Time Index, TTI), 혼잡지속시간, 혼잡 강도, Speed-Drop을 측정하고, 이를 종합하여 혼잡구간의 우선순위를 정하는 알고리즘을 개발하였다. Rui et al.(2018)는 평균속도, 도로밀도, 평균지체를 이용한 교통상태 식별을 위해 차량 임시 네트워크(Vehicular Ad hoc NETworkS, VANETs) 환경에서 차량 클러스터링 및 퍼지 평가를 기반으로 한 교통혼잡 감지 및 정량화 방법을 제안하였다. Susilo and Imanuel(2018)은 포화정도(degree of saturation)와 통행시간비율(travel time ratio)을 기준으로 교통혼잡 수준을 첨두시간혼잡(peak-hour congestion), 긴 혼잡(lengthy congestion), 일시적 혼잡(momentary congestion), 원활한 교통상황(smooth traffic) 총 4가지로 구분하는 방법론을 개발하였다. 이렇듯 해외에서는 개별차량 단위로 수집되는 교통데이터를 기반으로 혼잡상황을 식별하고, 혼잡의 우선순위를 평가하는 방법론이 활발하게 개발 및 적용되고 있다.

혼잡상황을 측정하는 방법은 Table 1과 같이 속도 기반, 통행시간 기반, 지체 기반, 서비스 수준 및 교통량기반으로 구분할 수 있다. 통행시간 기반 지표는 구간의 연장에 따라 통행시간의 차이를 보일 수 있으며, 직감적으로 상대적인 혼잡규모를 판단하기 어렵다. 지체 기반 지표는 실제 도로를 주행하면서 신호 및 기타 요인으로 정지한 시간을 산정해야 하므로, 현실적으로 데이터 수집이 어려운 한계점이 있다(Rao and Rao, 2016). 또한, 서비스 수준 및 교통량기반 지표 산정을 위해서는 전국 도로구간의 교통량 자료가 수집되어야 하지만 교통량 수집의 전국 커버리지는 3% 미만이며, 검지기 오차 등의 이유로 안정성(stability)이 떨어지는 한계점이 존재한다. 이러한 점을 고려했을 때 속도기반의 지표로 혼잡수준을 식별하는 것이 가장 적합하며, 범용적인 적용이 가능하다(Rao and Rao, 2012).

Table 1.

Congestion indices evaluation matrix

Congestion metric	Simplicity	Ease of data collection	Stability	Repeatability	Magnitude of congestion	City comparison	Continuous value
Speed	Y	Y	Y	Y	Y	N	Y
Travel time	Y	Y	Y	Y	N	N	Y
Delay	N	N	N	Y	N	N	Y
LOS and volume	Y	Y	N	Y	N	N	Y

도로구간에서 측정되는 속도자료를 기반으로 혼잡수준을 식별하는 대표적인 방법은 FHWA(2017)에서 제시하는 시공간 매트릭스(Spatio-Temporal Matrix, STM) 방법이 있다. STM은 x축을 공간범위, y축을 시간 범위, z축을 신뢰성(reliability) 범위로 하는 3차원 시공도를 통해서 D.I.V.E(Duration, Intensity, Variability, Extent)라고 하는 4가지 혼잡지표의 수준을 확인하는 방법이다. 대부분 속도자료 기반 혼잡판단 및 분석 연구에서는 이와 같은 4가지 지표를 많이 사용하며, 이를 종합하여 혼잡 우선순위를 평가하는 Impact factor를 개발하는 경우가 많았다(Hale et al., 2016b; Sisiopiku and Rostami-Hosuri, 2017).

기존 연구사례들에 대한 고찰결과를 종합하면 다음과 같다. 먼저, 동적 특성을 가진 혼잡과 병목을 판단하기 위해서는 개별차량 궤적자료(GPS)를 기반으로 기존 ITS 검지체계의 공간적 범위 한계를 극복할 필요가 있다. 그리고 혼잡상황 판단을 위해서 통행속도 기반의 지표를 사용하는 것이 적정할 것으로 판단된다. 또한 속도분포를 고려한 임계치를 기준으로 혼잡 발생을 판단한 경우가 많았으며, 혼잡 지속시간, 혼잡 강도, 혼잡 변동성, 혼잡구간 범위 등의 지표를 산출하여 혼잡수준을 분석하는 방법론이 국외에서 주로 적용되고 있었다. 마지막으로 각 지표를 종합한 Impact factor를 개발하여 우선순위를 평가하는 방법론도 필요할 것으로 판단된다. 따라서 본 연구에서는 국내외 혼잡분석과 관련한 기존연구 검토를 통해 시사점을 도출하고, 개별차량 이동궤적 수집이 가능한 차량 GPS 데이터(포인트)를 활용하였다. 또한 교통류 행태를 분석하기 위하여 기존 표준노드링크보다 약 3.5배 상세한 네트워크(한국교통연구원 6Lev 네트워크)를 활용하여 국내 모든 도로의 혼잡수준을 종합적으로 판단할 수 있는 방법론을 제안하고자 한다.

분석방법론

1. 분석개요

전국 도로 네트워크를 대상으로 동일한 기준으로 반복혼잡구간을 선정하는 것은 쉬운 일이 아니다. 본 연구에서는 도로구간의 반복혼잡우선순위 평가를 위한 기본 방향은 다음과 같다.

첫째, 전국을 동일한 기준으로 혼잡을 평가하기 위해서는 전국단위 교통정보 수집이 필수적이다. 기존 ITS 검지기(루프검지기, 레이더, 영상검지기 등)를 통한 교통정보 수집은 고정된 지점 및 구간으로 한정적이다. 따라서 ITS 인프라의 공간적 한계 극복을 위해 차량 GPS 자료를 활용하였다. 차량 GPS자료는 이동단말기 역할을 하며, 전국단위 소통정보 생성을 가능하게 한다. 다만, 좌표 기반의 GPS자료를 이용하여 신뢰성 있는 속도정보 생성을 위해서는 이상치 필터링(outlier filtering) 및 재구조화(reconstruction)를 위한 별도의 전처리 과정을 수행하였다. 이상치 필터링은 원시(raw) 데이터 상에서 동일 OBU ID를 기준으로 공간적 범위, 수집시간 외 데이터를 제거하는 작업을 수행하였다. 재구조화는 GPS 궤적오차 및 음영구간(터널/고층건물 등)에서 좌표가 손실되는 부분에 대하여 추정 및 보정을 통해 궤적자료를 재구조화하여 속도자료의 신뢰도를 개선하고자 하였다.

둘째, 혼잡여부 판단을 위해서는 별도의 기준설정이 필요하다. 본 연구에서는 혼잡교통류와 정상교통류를 구분하기 위하여 링크별 혼잡경계속도를 도로구간별로 산정하였다. 기존 연구에서 혼잡경계속도는 도로등급에 따라 모두 동일한 값을 적용하였다. 하지만 도로구간별 기하구조(차로수, 경사도 등) 및 구간특성(어린이보호구역, 톨게이트 등)이 다르므로, 현장특성을 반영할 수 없는 한계가 존재한다. 따라서 본 연구에서는 도로구간의 교통류 특성을 반영할 수 있는 혼잡경계속도를 적용하였다.

셋째, 도로구간의 혼잡정보뿐만 아니라 네트워크 차원에서 혼잡의 시공간적 영향을 판단하기 위해서는 별도 작업이 필요하다. 즉, 병목구간 산정 및 혼잡 영향권(시점, 종점)을 분석하기 위해서는 분석 네트워크에 교통축 정보가 속성값으로 구축되어야 한다. 따라서 교통축은 노선별로 상행/하행을 구분하였고, 연속된 링크 구간 판단을 위해 링크 순서를 구축하여 별도의 연산과정 없이 산정될 수 있도록 하였다.

넷째, 기존연구에서 혼잡구간 판단을 위해 제안된 지표는 대부분 단일 혼잡지표를 활용하였다. 하지만, 교통의 복잡성 및 역동성을 고려할 때 단일지표 보다는 다양한 지표를 융합하여 교통상황을 평가하는 것이 효율적일 수 있다. 본 연구에서는 자료수집 여건을 고려하여 통행속도 자료를 활용한 다양한 지표들을 선정하였고, 이를 종합적으로 반영하기 위하여 종합점수 산정 방법론을 제안하였다.

2. 데이터 구축

전국 도로구간의 소통정보 생성을 위해 차량 내비게이션 GPS 포인트 자료(2019년 2개월치)를 분석 네트워크를 기반으로 맵매칭된 자료를 이용하여 일자별 도로구간별 통행속도 분포(profile) 자료를 구축하였다. 링크통행속도 산출을 위해서는 데이터 전처리 및 가공작업이 선행되어야 한다. 데이터 전처리는 차량 GPS 검지오차로 인한 오류 데이터를 제거하였다. 또한, 포인트 자료를 이용하여 구간속도를 산정하기 위해서는 링크단위의 맵 매칭을 수행하였다. 속도정보를 교통운영 측면에서 활용하기 위해서는 최소 15분단위로 구축할 필요가 있다. 하지만 프로브 자료 보급률(약 1%)로 인한 네트워크 커버리지 문제로 1시간 단위로 속도분포를 구축하였다. 도로구간( $i$ ) 대표속도( $v$ ) 산정을 위해서 시간별( $t$ ) 프로브 샘플수( $n$ )가 30건/시 이상일 경우는 중위값(median), 그 밖의 경우에는 평균값(avg)을 적용하였다. 이는 모집단에서 표본집단의 크기가 충분히 클 경우( $n \geq 30$ ), 그 표본집단의 분포는 모집단의 분포의 모양과 관계없이 정규분포를 이룬다. 즉, 중심극한정리를 사용하여 표본의 통계치로 모집단의 모수치를 추정가능하다. 일반적으로 교통정보 산정 시 중위값이 더욱 신뢰할만한 값이므로 해당 값을 대푯값으로 설정하였다.

(1)

v (i, t) = \{\begin{cases} v_{m e d i a n}, i f n (i, t) \geq 30 \\ v_{a v g}, o t h e r w i s e \end{cases} \forall i, t

또한 프로브 자료의 보급률 문제로 일부 구간 및 시간대에서 프로브 대수가 0인 시간대가 다수 발생할 수 있다. 정보 미수집으로 인한 결측 구간의 존재는 교통정보 서비스의 품질에 상당한 악영향을 미칠 수 있다. 본 연구에서는 시계열 기반 방법론 중 적용이 간편하고, 해당 링크의 통행특성을 최대한 반영할 수 있는 누락자료 보정 방법론을 적용하였다. 즉, 인접 시간대의 이력 데이터만을 통해서 누락자료를 보정 수 있는 인접 자료 평균 방법과 평균 대체법(동일요일의 시간대 평균값)을 융합한 방법을 통해 누락자료 보정을 수행하였다.

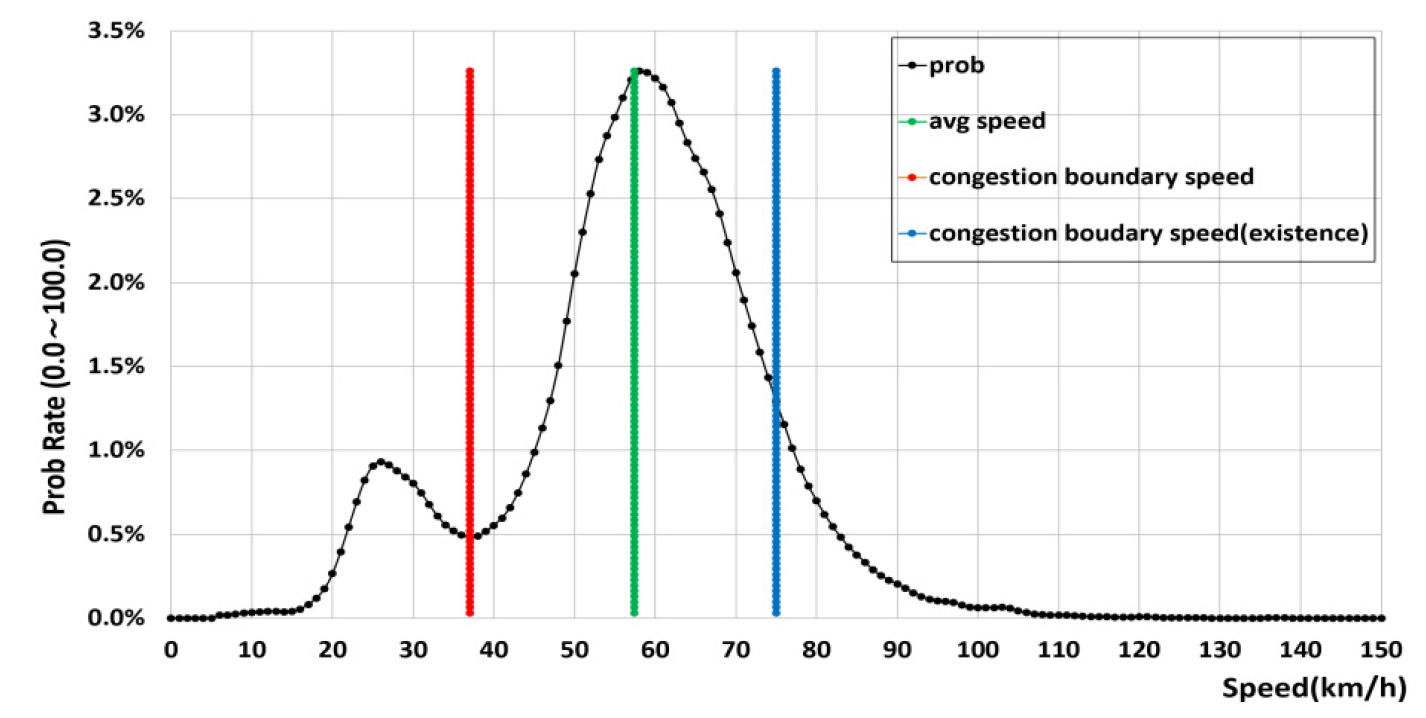
정상교통류와 혼잡교통류를 구분하기 위해서는 혼잡여부 판단을 위한 경계 값이 필요하다. 혼잡경계속도( $v_{b}$ ) 산정을 위해서 2017년 1년치 차량궤적 데이터를 이용하여 구축한 도로구간별 속도분포(1km 단위)를 활용하였다. 혼잡경계속도 산정 기본개념은 다음 그림과 같이 교통류가 와해되는 시점, 즉 서비스 수준 기준 LOS E와 F 사이를 혼잡경계속도로 정의하였다(Figure 1). 도로등급별 동일한 혼잡 기준을 설정할 경우 현장특성을 반영하는데 한계가 있을 것이다. 예를 들어 도심지의 어린이 보호구역 또는 고속도로 톨게이트 구간, 오르막차로 등은 주변 도로와 통행특성이 상이함에도 불구하고 동일한 기준으로 혼잡을 판단할 경우 합리적인 결과를 도출하는데 한계가 있을 것이다. 도로구간별 혼잡경계속도는 기존연구(Cheon et al., 2014) 결과를 활용한 것으로, 순응형 KNN 확률밀도(Adaptive K-Nearest Neighbor Probability Density)와 순응형 파라곤 창(Adaptive Paragon Window)을 이용한 최적화 모형의 이중구조 모형(Bi-level model)을 이용하여 혼잡경계값을 산정하였다.

https://static.apub.kr/journalsite/sites/kst/2021-039-02/N0210390205/images/kst_39_02_05_F1.jpg

Figure. 1

Concept of congestion boundary speed

도로구간에 발생한 혼잡은 해당구간의 혼잡강도도 중요한 요소지만, 혼잡이 발생한 시점정보(병목구간), 혼잡 영향권(혼잡전이길이) 등 네트워크에 미치는 영향도 매우 중요하다. 전국 네트워크를 대상으로 해당 혼잡지표를 산정하기 위해서는 별도의 네트워크 작업이 선행되어야 한다. 즉, 노선별 방향별 링크순서(시퀀스) 정보가 구축되어야 시공도 분석을 통해 병목구간 위치 및 혼잡구간길이 등에 대한 산정이 가능하며, 시스템 상에서 별도의 경로탐색 없이 빠른 연산이 가능하다. 따라서 본 연구에서는 링크순서 정보를 전국 고속도로와 일반국도를 대상으로 속성 값으로 입력하였다.

3. 교통혼잡 지표 개발

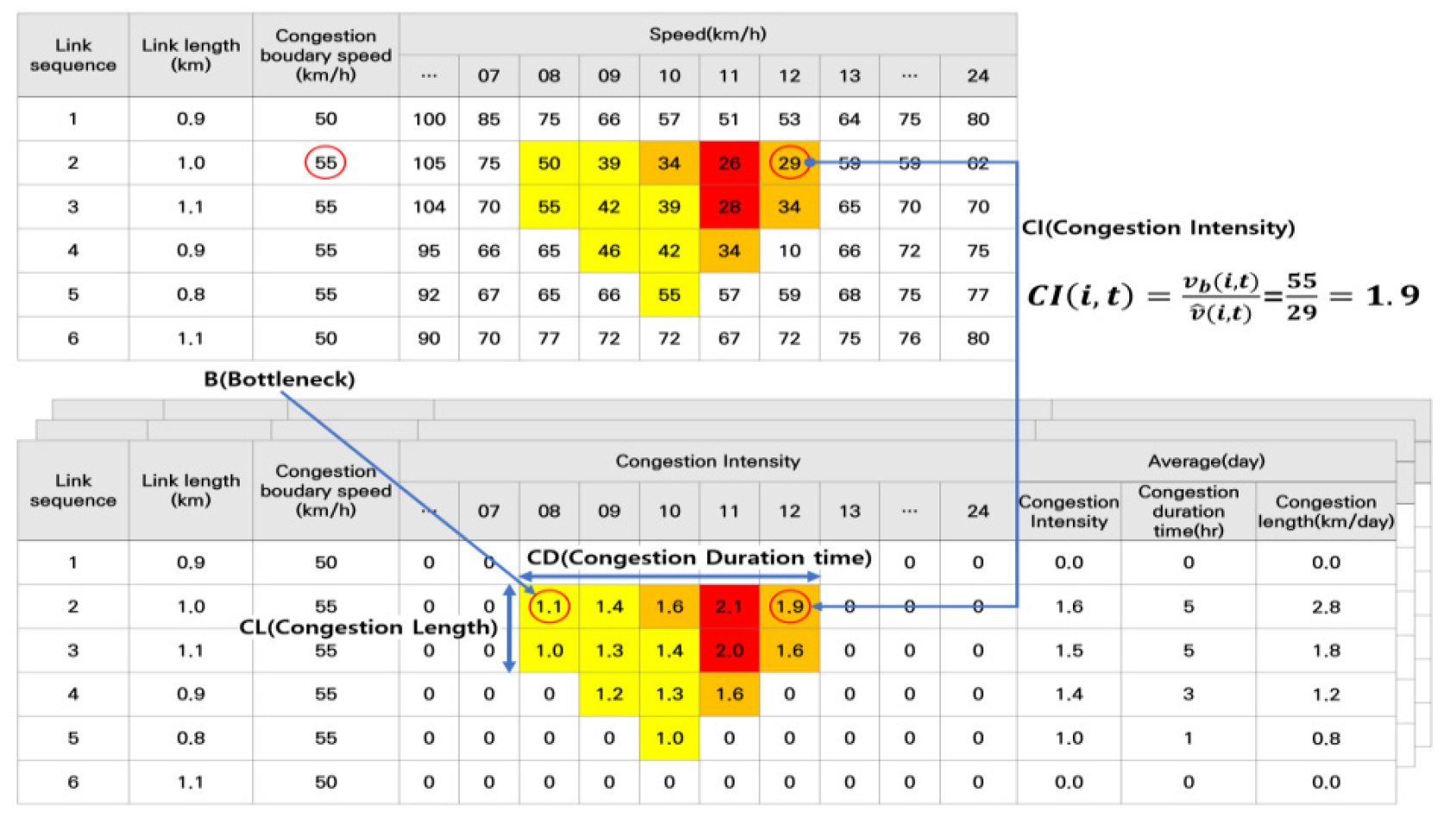
기존연구에서 혼잡구간 선정을 위하여 속도, 통행시간, 지체시간, 서비스 수준, 교통량 등을 기반으로 하는 다양한 지표들이 개발되었다. 데이터 수집 가능성과 범용적인 활용을 고려하여 본 연구에서는 반복혼잡구간 우선순위 평가를 위한 혼잡지표는 링크별 속도정보를 기반으로 산정 가능한 지표들로 설정하였다. 최종적으로 선택된 지표는 혼잡강도, 혼잡지속시간, 혼잡구간길이, 병목발생비율, 반복혼잡비율 총 5가지 지표이다(Figure 2). 지표들은 기본적으로 시간대별로 산정한 후 일 단위 평균값을 산정하였다. 단, 혼잡지속시간은 시간대별로 산정이 불가능하여 일 단위 평균값만 산정하였다. 혼잡지표별 정의 및 산정과정은 다음과 같다.

혼잡강도(Congestion Intensity, $C I$ )는 혼잡의 심각수준을 나타내는 지표로 혼잡경계속도( $v_{b}$ )를 평균속도( $\hat{v}$ )로 나눈 값이다. $C I$ 는 평균속도가 혼잡경계속도보다 높은 경우 0으로 산출되며, 혼잡이 발생하지 않은 것으로 판단한다. 여기서 혼잡발생여부( $C$ )는 혼잡일 경우 1, 비혼잡일 경우 0으로 산정한다. 기본적으로 일자별( $d$ )로 혼잡이 발생한 시간대 개수( $m$ ) 자료를 이용하여 일단위 평균혼잡도( $\bar{C I} (d, i)$ )를 산정한다. 특정기간에 대한 지표 산정을 위해서는 분석일수( $N$ )를 고려하여 평균값을 산정하였다.

(2)

C I (d, i, t) = \frac{v_{b} (i)}{\hat{v} (d, i, t)}, \begin{matrix} C (d, i, t) = \{\begin{cases} 1, i f C I (d, i, t) > 1.0 \\ 0, o t h e r w i s e \end{cases}, \forall d, i \\ C I (d, i, t) = \{\begin{cases} C I (d, i, t), i f C I (d, i, t) > 1.0 \\ 0, o t h e r w i s e \end{cases} \end{matrix} \bar{C I} (i) = \frac{\sum_{d = 1}^{N} \sum_{t = 1}^{24} C I (d, i, t)}{N \times m} \times 100, i f C I (d, i, t) > 1.0, \forall d, i, t

반복혼잡비율(Congestion Rate, $C R$ )은 전체 분석일수 중에 혼잡이 발생한 일수의 비율로 정의한다. 즉, 특정기간에 대한 반복혼잡비율 산정을 위해서 구간별 시간대별 혼잡비율을 산정한 후 $C R (i, t) > 0$ 인 시간대 값을 평균화하여 산정하였다. 이는 구간별 혼잡지속시간 지표가 별도로 산정되므로, 시간대별 혼잡이 발생한 시간대만을 대상으로 평균화하였다.

(3)

\bar{C R} (i, t) = \frac{\sum_{d = 1}^{N} C (d, i, t)}{N} \times 100, i f C (d, i, t) = 1.0, \forall d, i, t \bar{C R} (i) = \frac{\sum_{t = 1}^{24} C R (i, t)}{m} \times 100, i f C R (i, t) > 0

혼잡지속시간(Congestion Duration time, $C D$ )은 혼잡발생 시점에서 종료시점까지의 시간길이를 의미한다. 지표값 산정은 링크별 시간대별 혼잡강도가 1.0 이상인 경우의 시간대를 합산하여 일단위로 지표를 산정한다. 또한, 특정기간 단위 지표 산정을 위해서 전체 분석일수를 기준으로 평균값을 산정하였다.

(4)

\bar{C D} (i) = \frac{\sum_{d = 1}^{N} \sum_{t = 1}^{24} C (d, i, t)}{N} \times 100, \forall d, i, t

혼잡구간길이(Congestion Length, $C L$ )는 혼잡이 발생한 위치부터 최종 혼잡이 종료된 지점까지의 공간적 범위를 의미한다. 혼잡이 발생하는 경우 충격파로 인해 상류부로 혼잡이 전이되는 만큼 혼잡에 대한 영향을 판단하기 위해서는 중요한 지표이다. 지표값 산정은 우선 링크별( $i$ ) 시간대별( $t$ )로 $C (d, i, t) = 1$ 인 경우 혼잡이 종료된 지점까지의 링크 연장을 합산한다. 여기서, 혼잡이 다중구간에서 발생할 경우 해당구간( $i, i + 1 \dots$ )에서 혼잡종료구간까지의 연장의 합을 의미한다. 일 단위 평균값을 산정하기 위하여 시간대별로 산정된 $C L (d, i, t)$ 을 합산한 후 혼잡이 발생한 시간대 개수( $m$ )를 나누어 산정하였다. 특정기간 단위 지표를 산정은 전체 분석일수를 기준으로 평균값을 산정하였다.

(5)

C L (d, i, t) = \sum_{i = 1}^{n} l e n g t h (i), \{\begin{matrix} i f C (d, i, t) = 1 \\ s . t . C (d, i, t) = 0 t h e n s t o p \end{matrix}\}, \forall d, i, t \bar{C L} (i) = \frac{\sum_{d = 1}^{N} \sum_{t = 1}^{24} C L (d, i, t)}{N \times m}

병목구간( $B$ )은 시공간적으로 혼잡이 발생하는 지점을 의미한다. 병목구간을 판단하기 위하여 노선별 교통축 자료(링크순서)를 구축하였고, 시공도 분석을 통해 시공간적으로 혼잡이 최초로 발생하는 시공간 지점을 병목구간으로 선정하였으며, 병목구간일 경우 $B (d, i, t) = 1$ 로 산정하였다. 병목발생비율(Bottleneck Rate, $B R$ ) 산정은 특정기간 중 병목구간으로 선정된 일수의 비율을 통해 산정되며, 기본적으로 구간별 시간대별로 산정한 후 병목구간이 발생한 시간대 개수를 활용하여 구간의 평균값을 산정한다.

(6)

\bar{B R} (i) = \frac{\sum_{t = 1}^{24} \sum_{d = 1}^{N} B (d, i, t)}{m \times N} \times 100, i f B (d, i, t) = 1, \forall d, i, t

https://static.apub.kr/journalsite/sites/kst/2021-039-02/N0210390205/images/kst_39_02_05_F2.jpg

Figure. 2

Congestion index concept

4. 반복혼잡 우선순위 평가방법(종합점수)

본 연구에서 반복혼잡구간 산정 방법론의 주요 목적은 다양한 혼잡지표를 이용하여 혼잡수준을 종합적으로 파악하고, 개선대책 마련이 시급한 구간의 우선순위를 분석하는 것이다. 여기서, 반복혼잡 우선순위 분석을 위해서는 개별지표 산출 값을 하나의 평가지수로 종합하는 과정이 필요하다.

두 개 이상의 지표를 종합하여 하나의 평가지수를 개발할 때, 각 지표( $k$ )의 평균( ${\bar{x}}_{k}$ )과 표준편차( $σ_{k}$ )가 다르거나, 측정 단위가 다른 경우 지표 간 직접적인 비교에는 한계가 있다. 따라서 지표 간의 차이를 최소화하기 위해서는 표준화 과정이 필수적이라 할 수 있다. 지표 표준화와 관련하여 다양한 방법론을 검토한 결과 본 연구에서는 Equation 7과 같이 지표별 평균값과 표준편차를 활용한 $T - S c o r e$ ( $t_{k}^{i}$ ) 표준화 방법을 적용하였다. 본 방법을 적용한 이유는 이상치로 인해 결과가 왜곡되는 문제를 최소화하고, 지표별 동일한 분포의 형태로 변환하기 위한 목적으로 선정하였다. $T - S c o r e$ 표준화 방법은 여러 그룹의 지표 값을 기준 평균( $\bar{x} = 50$ ) 및 표준편차( $σ = 10$ )인 분포 상태를 갖도록 지표값을 변환한 점수로, 자료의 수치가 평균으로부터 표준편차의 몇 배 정도 떨어져 있는지를 표준화한 값을 의미한다. 도로등급별로 지표들의 평균 및 표준편차는 큰 차이를 보이므로 전국 도로를 대상으로 표준화할 경우 특정 도로등급의 혼잡이 크게 산정될 수 있다. 실제 일평균 기준으로 고속도로와 일반국도를 살펴보면 평균속도는 103km/h, 62.5km/h, 표준편차는 11.2km/h 20.5km/h로 상당히 큰 차이를 보이는 것으로 분석되었다. 따라서 본 연구에서 표준화 시 도로등급별로 평균과 표준편차를 산정하여 표준화를 수행하였다.

(7)

{\bar{x}}_{k} = \frac{\sum_{i = 1}^{n_{k}} x_{k}^{i}}{n_{k}}, σ_{k} = \sqrt{\frac{\sum_{i = 1}^{n_{k}} (x_{k}^{i} - {\bar{x}}_{k})}{n_{k} - 1}}, \forall i, k t_{k}^{i} = \bar{x} + (\frac{x_{k}^{i} - {\bar{x}}_{k}}{σ_{k}}) \times σ

반복혼잡 우선순위 산정을 위하여 5가지 지표를 선정하였고, 지표들의 절대적인 크기의 차이로 인한 영향력을 최소화하기 위하여 표준화를 수행하였다. 하지만, 본 연구에서 선정한 5가지의 혼잡지표가 모두 동일한 중요도를 가진다고 보기 어렵다. 따라서 혼잡지표들의 상대적 중요도 산정을 위하여 9점 척도로 이원 비교하는 방식의 AHP 설문조사를 수행하였다. AHP조사는 교통분야 전문가 15명을 대상으로 수행하였고, 분석결과는 Table 2와 같다. 가중치 결과는 조사 집단에 따라 차이를 보일 수 있으므로 절대적인 값은 아니다.

Table 2.

result of congestion index relative importance (weight)

Contents	$\bar{C I}$ (congestion intensity)	$\bar{C R}$ (congestion rate)	$\bar{C D}$ (congestion duration time)	$\bar{C L}$ (congestion length)	$\bar{B R}$ (bottleneck rate)
Weight	0.204	0.204	0.372	0.166	0.054

반복혼잡 우선순위 판정을 위한 종합점수(Composite Score, $C S$ )는 도로구간별 지표별 가중치와 표준화 결과를 곱하여 모두 더하는 방식으로 Equation 8과 같이 최종적으로 산출하였다.

(8)

C S (i) = 0.204 \times \bar{C I} (i) + 0.204 \times \bar{C R} (i) + 0.372 \times \bar{C D} (i) + 0.166 \times \bar{C L} (i) + 0.054 \times \bar{B R} (i)

분석결과

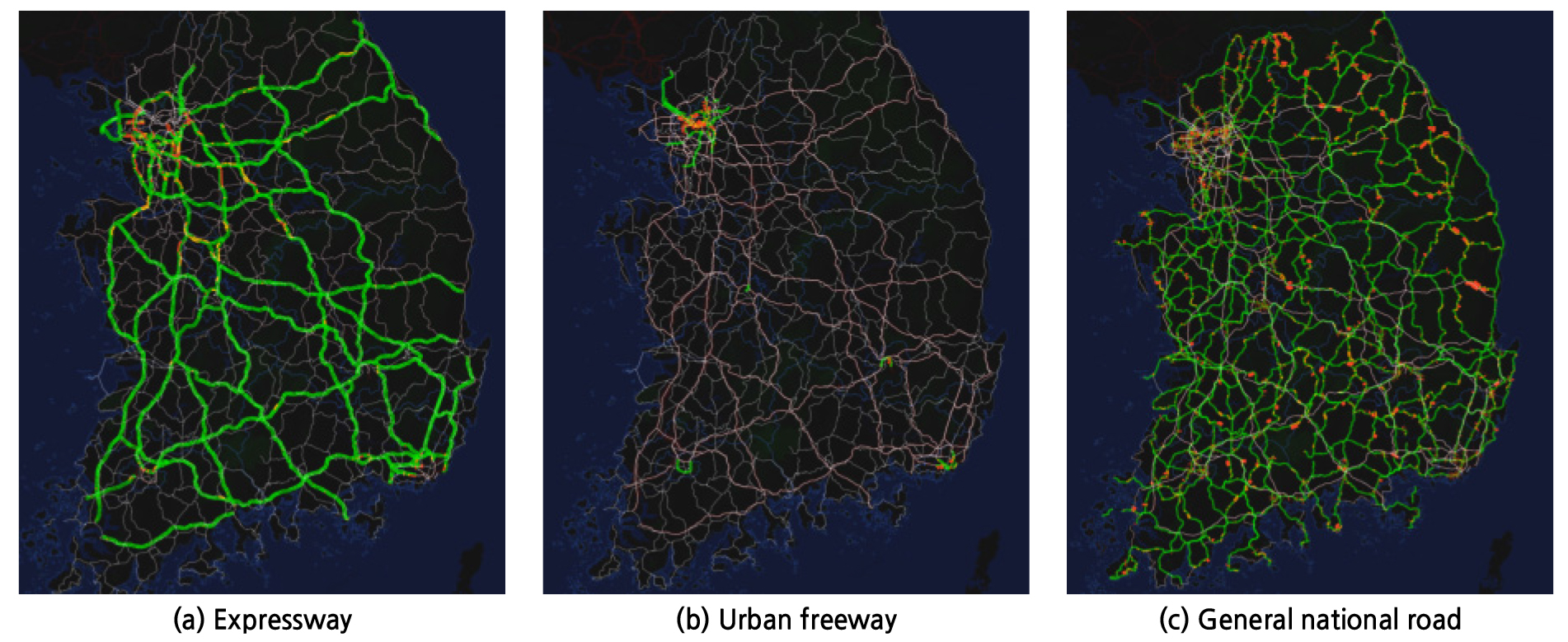
본 연구에서는 반복혼잡 우선순위를 판단하기 위하여 속도자료를 활용하여 산정 가능한 혼잡지표들을 선정하여 지표값을 산정하고, 지표별 가중치를 반영하여 종합점수를 산정하였다. Table 3은 2019년 12월 한 달치의 내비게이션 자료를 이용하여 고속도로 본선구간을 대상으로 혼잡지표들의 분석결과와 이를 기반으로 산정한 종합점수를 기준으로 한 우선순위를 분석한 결과이다. 앞서 설명한 바와 같이 내비게이션 GPS 자료는 전국 도로망에 대한 자료수집이 가능하므로, 공간정보를 활용하여 다양한 분석이 가능하다. Figure 3과 같이 링크 속성정보를 이용하여, 도로등급별(고속도로, 도시고속도로, 일반국도 등), 노선별, 차로수별, 지역별(시도, 시군구, 행정동), 도로유형별(일반도로, 교량, 터널 등) 등에 따른 현황분석이 가능하다.

Table 3.

Analysis result of recurrent congestion priority by expressway (top 20)

Rank	Link ID	Link information			Recurrent congestion priority analysis result
Rank	Link ID	Route	Lane	Length (km)	Congestion intensity	Congestion length (km)	Congestion duration (hour)	Congestion rate (%)	Bottleneck rate (%)	Composite score
1	57155541801	Gyeongbu	7	0.16	1.28	0.17	22.5	93	0	146.22
2	64540966801	Jungbunaeryuk	2	0.02	1.41	0.02	22.5	93	0	145.87
3	64540967201	Jungbunaeryuk	4	0.04	1.48	0.04	22.4	93	0	145.72
4	64841192701	Jungang	3	0.06	1.27	0.13	21.5	89	10	144.90
5	47660312801	Seoul ring	4	2.07	1.16	8.16	12.4	77	11	143.30
6	65632323601	Saemangeum pohang	2	0.1	1.62	0.12	20.6	85	4	139.51
7	77250375501	Donghae	2	0.09	3.12	0.17	18.9	78	5	134.59
8	57164643001	Gyeongbu	4	0.03	1.33	5.78	12	75	14	133.74
9	57164664101	Gyeongbu	4	0.01	1.6	4.95	13	76	10	133.12
10	47867926201	Seohaean	2	0.36	3.4	3.57	14	70	13	132.56
11	47660313001	Seoul ring	4	0.39	1.86	6.19	12.2	76	0	132.48
12	47660313301	Seoul ring	4	0.84	2.32	5.87	12.1	75	0	131.26
13	57164662201	Gyeongbu	4	0.55	1.4	5.86	12	74	5	131.03
14	64720988401	Namhae 3rd branch	2	0.24	1.9	0.37	18	74	7	130.46
15	64841193201	Jungang	3	0.09	1.12	0.14	18.9	78	0	130.44
16	57164664501	Gyeongbu	4	0.01	1.68	4.94	12.8	79	0	130.31
17	57164642401	Gyeongbu	4	0.59	2.08	2.25	15.6	81	0	130.04
18	57164822701	Gyeongbu	5	0.87	1.82	4.96	12.3	76	6	129.98
19	57164664601	Gyeongbu	4	0.05	1.66	4.95	12.9	75	0	129.46
20	57160661901	Gyeongbu	4	0.21	1.77	5.17	12.1	80	0	129.35

https://static.apub.kr/journalsite/sites/kst/2021-039-02/N0210390205/images/kst_39_02_05_F3.jpg

Figure. 3

Analysis result of recurrent congestion by level of roads (composite score)

고속도로, 도시고속도로, 국도를 대상으로 노선별 평가를 위하여 링크의 연장을 고려하여 종합점수를 가중평균 한 결과는 Table 4와 같다. 종합점수를 기준으로 살펴보면 서부간선도로가 가장 혼잡한 것으로 분석되었고, 뒤를 이어 경인고속도로, 서울외곽순환고속도로, 용인서울고속도로 등의 순으로 나타났다. 교통혼잡이 심한 노선은 대부분 교통량이 많은 수도권 주변의 노선들로 분석되었다. 일반국도의 경우에는 국도67호선(군위-칠곡), 국도87호선(철원-포천)이 가장 혼잡한 것으로 분석되었으며, 해당노선은 대부분 편도 1차로에 산간지역을 통과하는 도로인 것으로 나타났다.

Table 4.

Analysis result of recurrent congestion priority by route (top 15)

Rank	Route	Congestion intensity	Congestion length (km)	Congestion duration (hour)	Congestion rate (%)	Bottleneck rate (%)	Composite score
1	Seobu	1.69	1.64	7.32	42.04	2.31	61.98
2	Gyeongin	1.50	0.77	1.31	12.18	3.96	60.72
3	Seoul ring	1.36	0.79	1.30	12.33	1.77	59.99
4	Yongin Seoul	1.39	0.54	1.08	9.80	1.82	57.67
5	Gangbyeonbuk-ro	1.65	2.08	4.04	30.44	2.88	57.49
6	Olympic-daero	1.62	1.73	3.29	25.85	2.72	55.52
7	The 2nd gyeongin	1.09	0.47	0.63	8.81	1.70	55.31
8	Pyeongtaek siheung	0.94	0.79	0.49	7.37	0.98	55.28
9	Dongbu	1.47	1.18	3.71	27.04	2.68	55.06
10	Gyeongbu	0.65	0.36	0.86	6.44	0.63	54.07
11	General national road-67	2.02	0.13	3.82	17.72	3.33	53.59
12	Namhae 3rd branch	1.25	0.08	0.85	4.90	1.18	53.48
13	General national road-87	2.10	0.17	3.16	15.31	3.21	53.12
14	Ulsan	0.57	0.06	1.06	5.13	0.44	53.05
15	Jungbu	1.06	0.39	0.30	5.09	0.95	52.66

시도별로 살펴보면 서울특별시, 인천광역시, 부산광역시 등의 순으로 교통혼잡이 심각한 것으로 분석되었으며, 대부분 인구가 밀집된 광역시들이 높은 수준을 보였다(Table 5). 이밖에도 시군구, 행정동 단위로도 분석이 가능하며, 시계열 자료를 활용할 경우 정책시행에 따른 사전 ‧ 사후 평가 등에 활용이 가능할 것이다.

Table 5.

Analysis result of recurrent congestion priority by cities and provinces

Cities and provinces	Congestion intensity	Congestion length (km)	Congestion duration (hour)	Congestion rate (%)	Bottleneck rate (%)	Composite score
Seoul	1.76	0.41	4.18	21.61	3.13	55.32
Incheon	1.62	0.21	3.16	14.85	2.65	53.59
Busan	1.59	0.17	2.76	14.30	2.71	52.03
Daegu	1.97	0.12	2.38	12.38	2.75	51.64
Gwangju	1.89	0.11	2.48	12.50	2.79	51.40
Daejeon	1.79	0.08	2.13	11.04	2.40	50.93
Gyeonggi-do	1.61	0.13	1.92	10.34	2.20	50.62
Ulsan	1.55	0.08	2.09	10.44	2.30	50.21
Gangwon-do	1.46	0.12	1.60	9.13	2.22	49.92
Jeollabuk-do	1.53	0.10	1.65	9.30	2.25	49.86
Gyeongsangnam-do	1.46	0.10	1.58	8.83	2.08	49.66
Chungcheonbuk-do	1.44	0.09	1.55	8.70	2.00	49.46
Jeollanam-do	1.43	0.11	1.41	8.15	1.98	49.43
Sejong	1.35	0.06	1.85	9.36	1.93	49.29
Gyeongsangbuk-do	1.38	0.10	1.35	7.74	1.88	49.26
Chungcheongnam-do	1.38	0.09	1.49	8.36	1.91	49.19

결론

지금까지 교통소통정보를 제공하고 있는 ITS 정보는 지점검지 기반으로 정보제공의 공간적 범위가 전체 도로의 20%에 불과하고, 차량의 통행패턴 분석이 불가능하여 전국 도로의 세부 교통수준을 파악하는데 한계가 존재하였다. 교통 모빌리티 빅데이터(차량 GPS)는 기존 ITS 정보의 한계를 극복하고, 전국 단위 통행특성 분석이 가능하여, 이를 활용한 다양한 연구들이 진행되고 있다.

본 연구에서는 차량 내비게이션(GPS)의 위치 좌표를 수집데이터로 활용하여 전국 도로 구간의 시간대별 속도분포를 구축하였고, 속도자료를 기반으로 혼잡수준 판단을 위해 5가지 지표(혼잡강도, 혼잡구간길이, 혼잡지속시간, 반복혼잡비율, 병목발생비율)를 선정하였다. 이는 교통상황의 다양성을 고려할 때 단일지표를 통한 분석보다는 다양한 지표를 융합하여 평가하는 것이 더욱 효율적일 수 있기 때문이다. 따라서 다양한 지표를 활용한 종합적인 판단을 위하여 5가지의 혼잡지표와 지표별 가중치를 활용하여 종합평가를 수행하였다. 여기서, 지표별로 절대적인 값의 차이가 존재하므로 $T - S c o r e$ 표준화 방법을 이용하여 평균과 표준편차가 동일한 형태로 지표 값들을 표준화하였다. 또한, 지표별 가중치는 교통분야 전문가를 대상으로 AHP설문조사를 통해 산정하였다.

모빌리티 빅데이터 기반 도로부문 반복혼잡 우선순위 분석방법은 전국 도로의 혼잡수준을 평가 시 혼잡이 심각한 구간의 우선순위를 파악할 수 있으며, 도로등급별, 행정구역별 비교분석이 가능하며 일단위로 지표값을 산정하여 혼잡에 대한 시계열 분석이 가능하다. 이를 통해 교통혼잡 관련 통계자료, 교통정책 의사결정 지원, 도로 인프라 투자, 정책효과 사전 ‧ 사후 평가 등 다양한 혼잡 개선대책 마련에 도움을 줄 수 있을 것으로 기대한다.

본 연구에서 제안된 방법이 교통혼잡에 대한 현황분석뿐만 아니라 교통운영측면에서 효과적으로 활용되기 위해서는 향후 추가적인 연구 및 분석환경이 뒷받침이 되어야 할 것이다. 첫째, 혼잡발생요인의 다각적인 분석을 위해서 통행속도기반의 지표뿐만 아니라 교통량, 기후, 돌발상황 등을 반영할 수 있는 지표 개발 및 반영이 필요하다. 둘째, 반복혼잡 우선순위 분석결과 도로연장이 짧은 구간이 다수 포함되었다. 비록 본 연구에서 원시데이터(포인트 데이터)를 기반으로 공간정보 상에 맵매칭하여 기존 민간에서 제공된 링크 맵매칭 자료를 활용하였을 경우의 이상치 문제를 최소화하려고 노력하였지만, 그럼에도 불구하고 이상치 문제를 완전히 해결하는데 한계가 있다. 속도자료의 신뢰성 문제 해결을 위해 링크 연장의 최소 기준에 대한 연구가 추가적으로 필요하다. 셋째, 본 연구는 반복혼잡구간 선정을 위해 종합점수 산정을 통해 상대적 평가를 수행하였지만, 혼잡수준에 대한 절대적 판단을 위해서는 기준설정과 관련한 연구가 필요하다. 넷째, 교통운영측면에서 활용되기 위해서는 지표값은 최소 15분단위로 구축이 필요하다. 본 연구에서는 프로브 자료의 보급률로 인한 네트워크 커버리지 문제로 1시간 단위로 속도분포를 구축하였지만, 추가적인 데이터 확보를 통해 해결이 가능할 것이다. 마지막으로, 일정 기간 누적된 이력자료를 기반으로 장래 혼잡패턴 예측 알고리즘 개발 연구를 통해 교통 서비스 수준 향상방안 및 교통운영 서비스 제공 시 활용이 가능할 것이다.

Funding

This work is supported by the Korea Agency for Infrastructure Technology Advancement (KAIA) grant funded by the Ministry of Land, Infrastructure and Transport (Grant 19TLRP-B148671-02).

알림

본 논문은 대한교통학회 제82회 학술발표회(2020.3)에서 발표된 내용을 수정 ‧ 보완하여 작성된 것입니다.

References

Cheon S., Park I., Park Y., Kim S. (2014), Improving Estimation for Road Traffic Congestion Cost Using Car Navigation Information, The Korea Transport Institute.

Elhenawy M., Chen H., Rakha H. (2015), Traffic Congestion Identification Considering Weather and Visibility Conditions Using Mixture Linear Regression, Transportation Research Board 94th Annual Meeting. 10.5220/0005791400390048

FHWA (2016), 2015 Urban Congestion Trends: Communicating Improved Operation with Big Data, Accessed August, https://ops.fhwa.dot.gov/publications/fhwahop16032/fhwahop16032.pdf.

FHWA (2017), Recurring Traffic Bottlenecks: A Primer Focus on Low-Cost Operational Improvements (Fourth Edition), Accessed November, https://ops.fhwa.dot.gov/publications/fhwahop18013/fhwahop18013.pdf.

Hale D., Hajbabaie A., Ma J., Hu J., Park H., Bared J. (2016a), Proposed Data-Driven Performance Measures for Comparing and Ranking Traffic Bottlenecks, Transportation Research Procedia, 15, 483-494. 10.1016/j.trpro.2016.06.041

Hale D., Jagannathan R., Xyntarakis M., Su P., Jiang X., Ma J., Hu J., Krause C. (2016b), Traffic bottlenecks: identification and Solutions, U.S. Department of Transportation Federal Highway Administration.

He F., Yan X., Liu Y., Ma L. (2016), A Traffic Congestion Assessment Method for Urban Road Networks Based on Speed Performance Index, Procedia Engineering, 137, 425-433. 10.1016/j.proeng.2016.01.277

Kidando E., Moses R., Ozguven E., Sando T. (2017), Evaluating Traffic Congestion Using the Traffic Occupancy and Speed Distribution Relationship: An Application of Bayesian Dirichlet Process Mixtures of Generalized Linear Model, Journal of Transportation Technologies, 7(3), 318-335. 10.4236/jtts.2017.73021

Lomax T. J. (1997), NCHRP Report 398: Quantifying congestion: Volume 1, Transportation Research Board.

Lund A., Pack M., Plaisant C., Franz M. (2017), Algorithms for Identifying and Ranking Bottlenecks Using Probe Data, Transportation Research Board 96th Annual Meeting.

Rao A., Rao K. (2012), Measuring Urban Traffic Congestion-a review, International Journal for Traffic and Transport Engineering, 2(4), 286-305. 10.7708/ijtte.2012.2(4).01

Rao A., Rao K. (2016), Identification of Traffic Congestion on Urban Arterials for Heterogeneous Traffic, Transport Problems, 11(3), 131-142. 10.20858/tp.2016.11.3.13

Rui L., Zhang Y., Huang H., Qiu X. (2018), A New Traffic Congestion Detection and Quantification Method Based on Comprehensive Fuzzy Assessment in VANET, KSII Transactions on Internet and Information Systems, 12(1), 41-60. 10.3837/tiis.2018.01.003

Sisiopiku V. P., Rostami-Hosuri S. (2017), Congestion Quantification Using the National Performance Management Research Data Set, Data, 2(4), 39. 10.3390/data2040039

Stopher P. (2004), Reducing Road Congestion:A Reality Check, Transport Policy, 11(2), 117-131. 10.1016/j.tranpol.2003.09.002

Susilo B., Imanuel I. (2018), Traffic Congestion Analysis Using Travel Time Ratio and Degree of Saturation on Road Sections in Palembang, Bandung, Yogyakarta, and Surakarta, MATEC Web of Conferences, 181, Article Number 06010. 10.1051/matecconf/201818106010

Thakur S., Singh R. (2016), A Review of Traffic Congestion Problem and Various Automated Traffic Measurement Sensors and Technique, Indian Journal of Science and Technology, 9(47), 1-16. 10.17485/ijst/2016/v9i47/106902

Journal of Korean Society of TransportationISSN:1229-1366(Print) 2234-4217(Online)대한교통학회

Preview

Recurrent Congestion Severity Priority Analysis Methodology Based On Mobility Big-Data

ABSTRACT

MAIN

Table 1.

Congestion indices evaluation matrix

(1)

Figure. 1

Concept of congestion boundary speed

(2)

(3)

(4)

(5)

(6)

Figure. 2

Congestion index concept

(7)

Table 2.

result of congestion index relative importance (weight)

(8)

Table 3.

Analysis result of recurrent congestion priority by expressway (top 20)

Figure. 3

Analysis result of recurrent congestion by level of roads (composite score)

Table 4.

Analysis result of recurrent congestion priority by route (top 15)

Table 5.

Analysis result of recurrent congestion priority by cities and provinces

References