Incentive Strategy to Improve Passenger Convenience and Operation Efficiency of Demand-Responsive Transportation Systems

Sang-Wook Han; Dong-Kyu Kim; Sedong Moon

doi:10.7470/jkst.2024.42.2.180

Preview

Article

Journal of Korean Society of Transportation. 30 April 2024. 180-195
https://doi.org/10.7470/jkst.2024.42.2.180

Incentive Strategy to Improve Passenger Convenience and Operation Efficiency of Demand-Responsive Transportation Systems

수요 응답형 교통 시스템의 승객 편의성 및 운영 효율성 제고를 위한 인센티브 전략 수립

Sang-Wook HAN¹

Dong-Kyu KIM²

Sedong MOON³^*

한 상욱¹

김 동규²

문 세동³^*

¹Ph. D. Candidate, Department of Civil and Environmental Engineering, Seoul National University, Seoul 08826, Korea

²Professor, Department of Civil and Environmental Engineering, Seoul National University, Seoul 08826, Korea, Adjunct Professor, Institute of Construction and Environmental Engineering, Seoul National University, Seoul 08826, Korea

³Postdoctoral Researcher, Institute of Construction and Environmental Engineering, Seoul National University, Seoul 08826, Korea

¹서울대학교 건설환경공학부 박사수료

²서울대학교 건설환경공학부 교수, 서울대학교 건설환경종합연구소 겸임연구원

³서울대학교 건설환경종합연구소 연수연구원

^{*Corresponding Author}

ABSTRACT

The demand for a convenient transportation option is continuously increasing, but traditional public transportation systems operate on fixed routes, causing inconvenience for passengers by requiring them to travel from their departure points to designated stations. Demand responsive transportation (DRT) has been introduced as a solution to address these issues. DRT services plan and operate routes based on passenger demand, offering convenience to passengers. However, there are several challenges in operating DRT. First, DRT passengers want to reach their destinations quickly, while DRT operators aim to maximize revenue by accommodating as many passengers as possible. Also, passengers make choices between DRT and public transportation by comparing their travel time and fares: potential passengers are less likely to choose DRT when its travel time gets longer. Additionally, as additional reservations extend travel routes and times, reserved passengers do not want any additional reservations, while those making reservations hope for their requests to be accepted. Amid these conflicting relationships between DRT passengers and operators, mode choices between DRT and public transportation, and conflicts between reserved and reserving passengers, this study proposes an incentive system to enhance the convenience for DRT passengers and improve operational efficiency. The proposed incentive system rewards passengers for moving to other passengers' boarding or alighting points, reducing detours and shortening travel times for DRT passengers. However, if incentives are too high, DRT operators may experience reduced income. To consider these conflicts, we used a mode choice model between public transportation and DRT, formulated the problem as the multi-objective mixed-integer nonlinear programming, and solved the NP-hard combinatorial optimization problem using a heuristic algorithm. This study conducted the case study for the network of Incheon, Korea, and used taxi data to reflect passenger travel behavior. The Pareto optimal set obtained provides a balanced solution for both DRT passengers and operators. It is revealed that setting incentives at 8% or 12% of the basic DRT fare is the most effective level.

Keywords

demand responsive transportation

dynamic programming

incentive

mode choice model

multi-objective optimization

편리한 교통 수단에 대한 수요는 계속 증가하고 있지만 기존의 대중교통은 고정된 경로를 가지고 운행되어 승객들은 출발지에서 정류장까지 이동해야 하는 불편함이 존재한다. 수요 응답형 교통(Demand Responsive Transportation, DRT)은 이러한 문제를 해결하기 위한 수단으로 도입되었다. DRT는 승객의 요구에 따라 경로를 계획하고 운영하는 서비스로 승객에게 편리함을 제공하지만 DRT 운영에는 몇 가지 어려움이 있다. 먼저 DRT 승객은 빠르게 목적지에 도착하고자 하며 DRT 운영자는 수입을 극대화하기 위하여 최대한 많은 승객을 수용하려 한다. 또한 승객들은 DRT와 대중교통의 통행시간, 요금 등을 비교하여 교통수단을 선택하는데, DRT의 통행시간이 길어지면 잠재적인 승객들이 DRT를 선택하지 않을 가능성이 높아진다. 그리고 추가 예약이 발생하면 운행경로와 통행시간이 증가하므로, 이미 예약된 승객들은 추가 예약이 발생하지 않기를 원하는 반면, 예약하려는 승객들은 본인의 예약이 거절 없이 승낙되기를 바란다. 이와 같은 DRT 승객과 운영자 사이의 상충관계, DRT와 대중교통 사이의 수단 선택 과정, 예약된 승객과 예약하는 승객의 상충관계 속에서, 본 연구는 DRT 승객의 편의 및 운영 효율성을 제고하기 위한 인센티브 시스템을 제안한다. 제안된 인센티브 시스템에서는 승객이 다른 승객의 승차 지점이나 하차 지점으로 이동하여 같이 승하차하면 인센티브를 받게 되며, 이로 인해 차량의 우회가 줄어들어 DRT 승객의 이동시간이 단축된다. 그러나 인센티브가 너무 높으면 DRT 운영자의 수입이 감소한다. 본 연구에서는 이러한 점을 반영하기 위해 대중교통과 DRT 사이의 수단선택 모형을 사용하고, 다중 목적 혼합 정수 비선형 프로그래밍을 이용해서 문제를 수식화하였으며, NP-hard 문제로 알려진 조합최적화를 사용하여 휴리스틱 알고리즘으로 해를 탐색하였다. 본 연구에서는 인천광역시를 대상으로 사례연구를 진행하였으며 승객들의 통행 행태 반영을 위해 택시데이터를 사용하였다. 도출된 Pareto optimal set을 통해 DRT 승객과 운영자 모두에게 균형잡힌 해결책을 찾을 수 있다. 본 연구에서는 인센티브를 DRT 기본요금의 8% 또는 12% 수준으로 설정하는 것이 가장 효과적인 것으로 나타났다.

키워드

수요 응답형 교통

dynamic programming

incentive

수단 선택 모델

multi-objective optimization

MAIN

서론
선행연구
연구 방법론
1. 문제 정의
2. DRT 최적화 과정
3. 수학적 수식
4. DRT와 대중교통 간 수단선택 모델
사례 연구
연구 결과
1. 승객 수와 도보 시간
2. 평균 통행시간과 평균 수입
3. Pareto-optimal set
4. 제언
결론

서론

편리한 교통 수단에 대한 요구는 지속적으로 증가하고 있다. 대중교통은 고정된 노선이 있는 교통수단으로, 승객들은 출발지에서 정류장까지, 정류장에서 목적지까지 이동해야 하는 번거로움이 있다. 수요 응답형 교통(Demand Responsive Transportation, DRT)은 승객의 편의성을 향상시키는 수단으로 도입되었다. DRT는 수요를 기반으로 차량의 경로를 계획 및 운영하는 맞춤형 교통 서비스이다(Vuchic, 2007). DRT는 고정된 노선이 없이 승객들의 출발지, 도착지에 따라 노선이 결정되는 준대중교통 서비스로, DRT 차량은 승객을 출발지에서 픽업하여 목적지까지 운송한다. 물론 DRT 역시 대중교통과 마찬가지로 대기시간이 필요하지만, DRT 차량은 승객의 출발지와 목적지를 직접 방문하므로 출발지에서 승차 정류장까지, 하차 정류장에서 최종 목적지까지 접근하는 시간이 불필요하다.

이러한 장점에도 불구하고, DRT는 계획 및 운영에 많은 어려움을 겪고 있다. 먼저, DRT 승객과 DRT 운영자가 서로 상충하는 관계에 있기 때문에 두 이해당사자(운영자 및 승객)를 모두 만족시키는 DRT 서비스를 설계하는 것은 어렵다. DRT 승객은 최대한 빠른 시간내에 목적지에 도달하기를 원하는 반면, 운영자는 수입을 최대화하기 위하여 합승을 허용하는 DRT 차량은 가능한 많은 승객 요청을 수용하려고 하며, 이로 인해 다른 승객을 픽업하고 내려주기 위해 우회를 하게 되어 경로가 연장된다. 우회가 발생하면 DRT의 이동 시간이 증가하게 되어 DRT 승객의 불편을 초래하고 DRT를 이용하려던 승객은 대중교통과 같은 다른 수단으로 전환될 수 있다. DRT 설계의 두 번째 어려움은 잠재적인 승객이 DRT와 대중교통을 비교하고 우세한 수단을 선택한다는 것이다. 승객은 도보 시간, 예상 대기시간, 예상 차내시간, 요금 등을 고려하여 교통수단을 선택한다. 따라서 DRT의 계획 및 운영에 있어서 잠재적인 승객들의 수단선택 행태를 고려해야 한다. 마지막으로 예약된 승객과 예약하려는 승객 간의 상충관계가 존재한다. 새로운 승객의 요청이 수락된다면 DRT 차량의 통행시간이 우회로 인해 증가하며, 이는 기존에 이미 예약되었거나 DRT를 이미 이용 중인 승객들의 불편을 초래한다. 따라서 DRT 설계 시, 승객 요청을 수용할지 여부를 결정하기 위한 기준을 설정해야 한다.

승객이 DRT 대신 대중교통을 선택하는 주된 이유는 DRT의 우회로 인한 이동 시간 증가 때문이다. 승객들이 다른 승객의 승차 지점으로 이동하여 같이 승하차하거나, 다른 승객의 하차 지점에서 같이 승하차할 때 인센티브를 제공받도록 하면, 각각의 승객들을 태우기 위한 우회가 감소하고 DRT 승객들의 통행시간이 절약된다. 인센티브 제공이 수입성에 부정적인 영향을 미칠 수도 있지만, 다른 한편으로는 DRT 통행시간이 감소하고 더 많은 승객들이 DRT를 이용하게 되면 오히려 더 큰 수입을 얻을 수 있으므로, 이를 고려한 적절한 인센티브 전략을 개발할 필요가 있다. 인센티브를 운영자에게 제공하는 경우 운영자가 인센티브를 받기 위해 비효율적으로 DRT를 계획하므로 DRT 운영에 부정적인 영향을 미칠 수 있다(Palmer et al., 2004). 그러나 본 연구의 인센티브 시스템은 DRT 승객에게 제공되며, 인센티브 시스템을 갖춘 DRT의 효율성을 고려하여 목적 함수와 수단 선택 모델을 구현하고자 한다. 선행 연구에서 고려되지 않은 수단 선택 모델을 적용함으로써 잠재적인 승객이 DRT와 대중교통을 비교하고 수단을 선택하는 행태를 구현한다.

따라서 본 연구에서는 DRT 운영자와 승객의 상충관계, 잠재적인 승객들의 수단 선택 행태, 예약된 승객과 예약하려는 승객의 상충관계를 모두 고려하고, DRT가 대중교통 대비 경쟁력을 가질 수 있게 하기 위한 인센티브 시스템을 제안한다. 이를 위해 동적 승객 요청을 기반으로 인센티브 시스템을 적용한 동적 DRT를 최적화하고, 인센티브 값을 변경하면서 민감도 분석을 수행하여 DRT 승객과 DRT 운영자 모두에게 적절한 인센티브 수준을 찾고자 한다. 본 연구에서는 동적 DRT 최적화 문제를 다중 목적 혼합 정수 비선형 프로그래밍(Multi-Objective Mixed Integer Nonlinear Programming, multi-objective MINLP)으로 표현함으로써, 총 이동 시간을 최소화하고 수입을 최대화하며 DRT 승객과 DRT 운영자 간의 최적의 타협점을 찾고자 한다. 결정 변수는 각 차량의 경로와 승객이며, 최적의 결정 변수를 찾기 위해 조합 최적화를 수행한다. 조합 최적화는 일반적으로 NP-hard 문제로, 이를 해결하기 위해 휴리스틱 알고리즘을 사용한다. 본 연구에서는 다중 목적 최적화에 적합한 Nondominated Sorting Genetic Algorithm II(NSGA-II)를 사용한다.

선행연구

지금까지의 DRT 연구는 다양한 관점과 목적을 가지고 수행되었다. 먼저 DRT 운영자의 관점에서는 운영 비용을 최소화하거나(Dessouky et al., 2003; Quadrifoglio et al., 2008; Nourbakhsh et al., 2012; Amirgholy and Gonzales, 2016; Guo et al., 2018; Wang et al., 2020) 수입을 극대화하기 위한(Lyu et al., 2019) DRT 차량의 경로 및 스케줄을 결정하는 연구가 많이 이루어졌다. DRT 운영에 가장 큰 영향을 미치는 요소 중 하나인 DRT 차량 운영 대수를 결정하는 연구도 수행되었다(Diana et al., 2006; Chevrier et al., 2012). DRT 승객의 관점에서는, 통행시간이 승객의 수단 선택에 큰 영향을 미치기 때문에 통행시간을 최소화하기 위한 연구가 많이 수행되었다(Nourbakhsh et al., 2012; Shen et al., 2012; Wang et al., 2020). 승객의 비용 또는 이동 시간을 목적함수로 설정하여 이를 최소화하기 위한 DRT 최적화 연구도 이루어졌다(Jaw et al., 1986; Amirgholy and Gonzales, 2016; Nourbakhsh et al., 2012; Guo et al., 2018). 공공의 관점에서는 온실가스를 고려한 환경 요인이 DRT 설계에 적용된 바 있다(Dessouky et al., 2003; Diana et al., 2007). DRT를 운영자, 승객, 공공 중 어느 한 이해관계자만의 관점에서 최적화한다면 다른 이해관계자들을 만족시키기 어렵다. 따라서 둘 이상의 이해당사자를 동시에 고려한 DRT 최적화 연구도 이루어졌다(Dessouky et al., 2003; Nourbakhsh et al., 2012; Amirgholy and Gonzales, 2016; Guo et al., 2018; Guo et al., 2019; Wang et al., 2020).

DRT는 이전에 예약된 승객 요청을 기반으로 DRT 차량의 경로를 계획하는 정적 DRT와 실시간으로 발생하는 승객 요청을 기반으로 DRT 차량의 경로를 업데이트하는 동적 DRT로 구분된다. 운영 및 설계의 복잡성으로 인해 정적 DRT에 대한 연구가 동적 DRT에 대한 연구보다 더 많이 수행되었다(Diana et al., 2006; Chevrier et al., 2012; Guo et al., 2018; Guo et al., 2019). 동적 승객 요청을 반영한다면 승객의 편의를 높이고 수입성을 증대할 수 있으며, 이를 위해 DRT 차량의 경로가 각 시간대에서 동적 요청을 반영하여 최적화되는 연구들이 진행되었다(Dessouky et al., 2003; Quadrifoglio et al., 2008; Amirgholy and Gonzales, 2016; Lyu et al., 2016; Lyu et al., 2019; Wang et al., 2020). DRT는 일반적으로 door-to-door 서비스로 운영되지만, 이 서비스는 DRT 차량의 불가피한 우회로 인해 이동시간이 크게 증가하는 단점이 있다. 이 문제를 해결하기 위해 승객 요청을 시공간적으로 군집화하고 각 군집의 중심을 승차 및 하차 지점으로 설정하여 DRT 차량의 경로를 설계하는 DRT의 한 분야인 customized bus가 제안되기도 하였다(Lyu et al., 2016; Guo et al., 2018; Guo et al., 2019; Lyu et al., 2019; Wang et al., 2020). Customized bus는 일반적인 door-to-door 형태의 DRT보다 우회 정도가 적어지지만, customized bus를 이용하는 승객은 출발지에서 승차 지점으로 이동하고 하차한 후 목적지로 이동해야 하므로 first-mile과 last-mile 문제가 발생한다. 운영 효율성을 높이기 위해 DRT 서비스 권역을 나누어 각 권역별로 DRT가 운영되는 전략도 제안된 바 있다(Quadrifoglio et al., 2008; Quadrifoglio and Shen, 2009; Shen et al., 2011). 하지만 이 경우에는 DRT 승객들이 다른 지역으로 이동할 때 환승해야 하는 불편함이 존재한다.

DRT 연구에서 실제 데이터가 없는 경우 가상으로 생성된 데이터를 사용하기도 한다(Diana et al., 2006; Chevrier et al., 2012; Nourbakhsh et al., 2012; Wong et al., 2014; Guo et al., 2018; Wang et al., 2020). 가상 데이터를 사용하는 경우 DRT 승객 요청을 무작위가 아닌 확률적으로 생성함으로써 보다 현실적인 DRT 최적화를 시도하기도 하였다(Chevrier et al., 2012; Nourbakhsh et al., 2012; Diana et al., 2006). 그러나 확률적으로 생성된 승객 요청은 실제 여행 패턴을 반영하지 않으므로 이를 고려하기 위해 택시 데이터를 사용하기도 하였다(Lyu et al., 2016; Lyu et al., 2019).

승객은 DRT를 대중교통과 유사한 대안으로 간주하고 대중교통과 DRT를 비교하여 통행 수단을 선택한다(Papanikolaou et al., 2017). 선행 연구는 대중교통과 개인용 자동차 간 수단 선택이나 대중교통 간 수단 선택 행동에 집중해왔다(Asensio, 2002; Buehler, 2011; Hensher et al., 2012; Chen et al., 2017). 대중교통과 DRT 사이의 수단 선택 관련 연구로는 고정 노선 대중교통과 고정된 노선을 갖지 않는 교통수단 간의 수단 선택 행동을 조사한 연구와(Palmer et al., 2004) 대중교통과 DRT 사이의 수단선택 모형을 개발한 연구가 있다(Chavis et al., 2017).

연구 방법론

1. 문제 정의

본 연구에서 다루고자 하는 DRT 서비스에 대한 전제조건은 다음과 같다. 먼저, 승객이 DRT 승객용 애플리케이션 등을 통해 출발지와 도착지를 입력하면 DRT 운영자는 입력된 탑승 및 하차 위치를 파악할 수 있다. DRT 차량의 경로는 새로 수락된 탑승 요청을 반영하여 수시로 업데이트 된다. DRT는 두 대 이상의 차량이 door-to-door로 운영되며 수시로 탑승 요청을 체크한다.

승객들은 DRT와 대중교통에 대해서 예상 대기시간, 예상 차내 시간, 최대 지연시간, 요금 및 도보 시간을 비교하고 더 효율적인 수단을 선택한다. 수단 선택 모델은 이러한 승객들의 선택 행동을 반영하기 위한 중요한 요소이다. DRT 차량이 요청을 수락하면 이를 위해 경로가 수정되고 보통은 기존 경로보다 더 우회하는 경로가 되어 승객들의 통행시간이 증가하게 된다. DRT 운영자는 수입 창출을 위해 가능한 한 많은 승객을 수용하려고 노력할 것이며, 이로 인한 DRT 통행시간의 증가는 승객들에게 불편을 끼친다. 따라서 승객들에게 제공되는 서비스의 질을 일정 수준 이상으로 유지하기 위해서는 최대 지연시간을 설정해야 한다. 최대 지연시간은 전체 DRT 운영에 영향을 미치는 주요 제약 조건이다. 본 연구에서는 승객들이 수용할 수 있는 최대 지연시간이 당초 예정된 통행시간에 비례한다고 가정한다. 이때 각 승객의 최대 지연시간은 당초 예정된 통행시간에 일정 비율(최대 지연시간 비율)을 곱한 값이 된다. 예를 들어, DRT 운영자가 설정한 최대 지연시간 비율이 50%라면, 당초 예정된 총 통행시간이 20분인 승객과 30분인 승객의 최대 지연시간은 각각 10분과 15분이다. 이들이 같은 DRT 차량을 이용하고 다른 승객이 없다면, 모든 DRT 승객을 만족시키기 위한 최종 최대 지연시간은 10분이다.

우회로 인한 과도한 통행시간 증가를 방지하기 위해 DRT 회사는 인센티브 전략을 택할 수 있다. 인센티브 전략은 승객들에게 요금 할인을 제공함으로써 승객들이 다른 승객의 승차 또는 하차 지점으로 이동하여 같이 승하차하도록 유도한다. 이를 통해 개별 승객들을 태우기 위한 DRT 차량의 우회가 줄어들고 DRT 승객들의 통행시간이 절약되도록 할 수 있다. 본 연구에서 DRT 요금은 거리비례제를 택한다. DRT는 실시간으로 경로가 바뀌어 거리비례제를 적용하기 힘들 수 있지만 승객들의 예약 시점에 안내된 거리 기반으로 요금을 부과하여 우회로 인한 거리 증가는 요금 증가로 이어지지 않게 하였다.

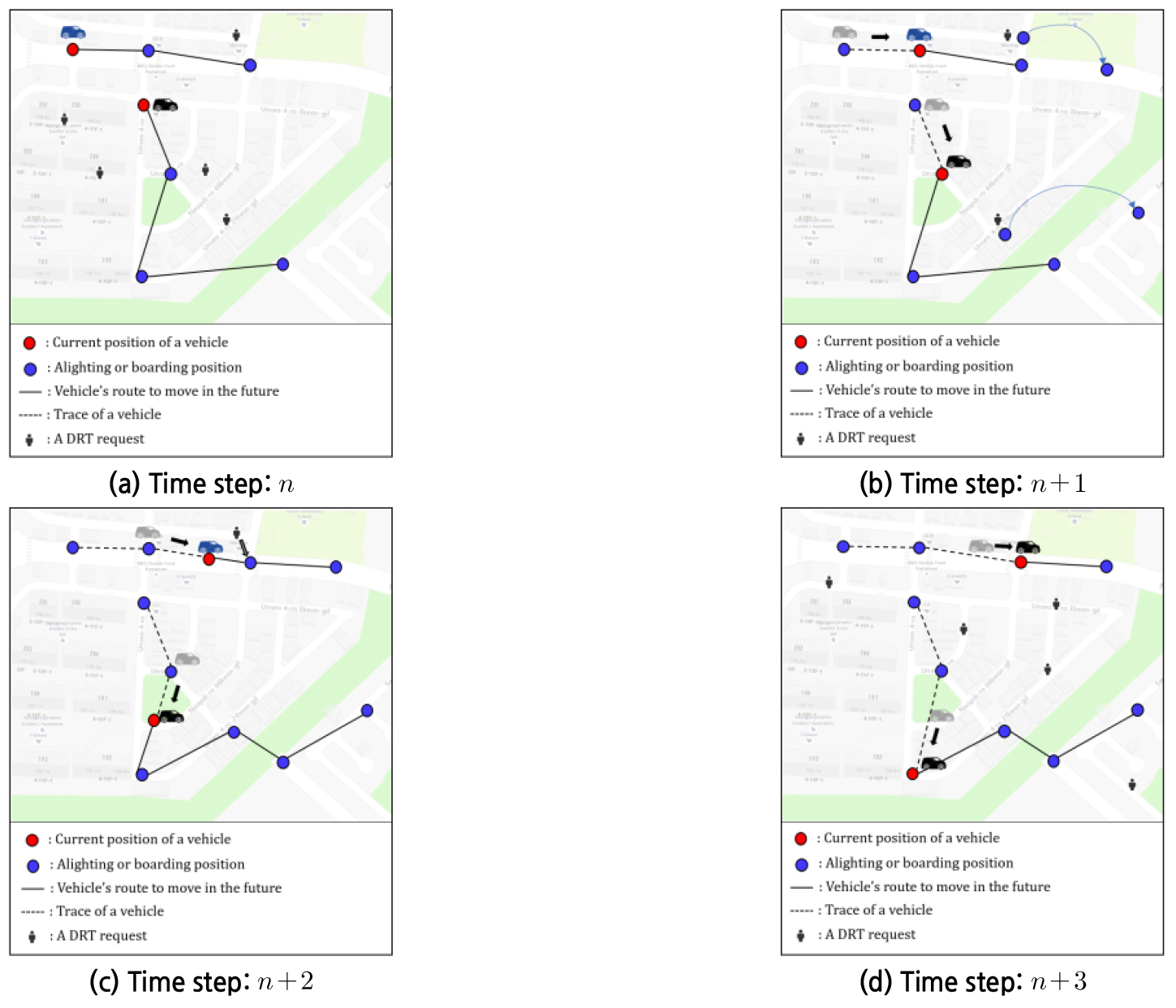
Figure 1은 예시를 통해 각 시점에서 DRT가 어떻게 운영되는지 설명한다. Figure 1(a)는 DRT 요청이 발생한 상황을 나타낸다. DRT 요청은 애플리케이션 등을 통해 출발지와 목적지를 입력한다. 일부 승객들은 다른 승객의 탑승 또는 하차 위치로 이동하기로 결정하여 할인된 요금을 지불한다. DRT 운영자는 요청 정보를 집계하고 제약 조건을 만족하는 승객의 요청을 수락한다. Figure 1(b)는 5건 중 2건의 요청이 수락된 상황을 보여준다. 이후 Figure 1(c)와 같이 DRT 차량의 경로는 새로 수락된 승객에 따라 업데이트된다. Figure 1(c)에서 수락된 2명의 승객 중 한 명은 다른 승객의 탑승 또는 하차 위치로 이동하여 탑승하기로 결정하였다. 이후 Figure 1(d)에 표시된대로 새로운 승객 요청이 다시 발생한다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420205/images/kst_2024_422_180_F1.jpg

Figure 1.

Examples of how DRT is operated in each time step

2. DRT 최적화 과정

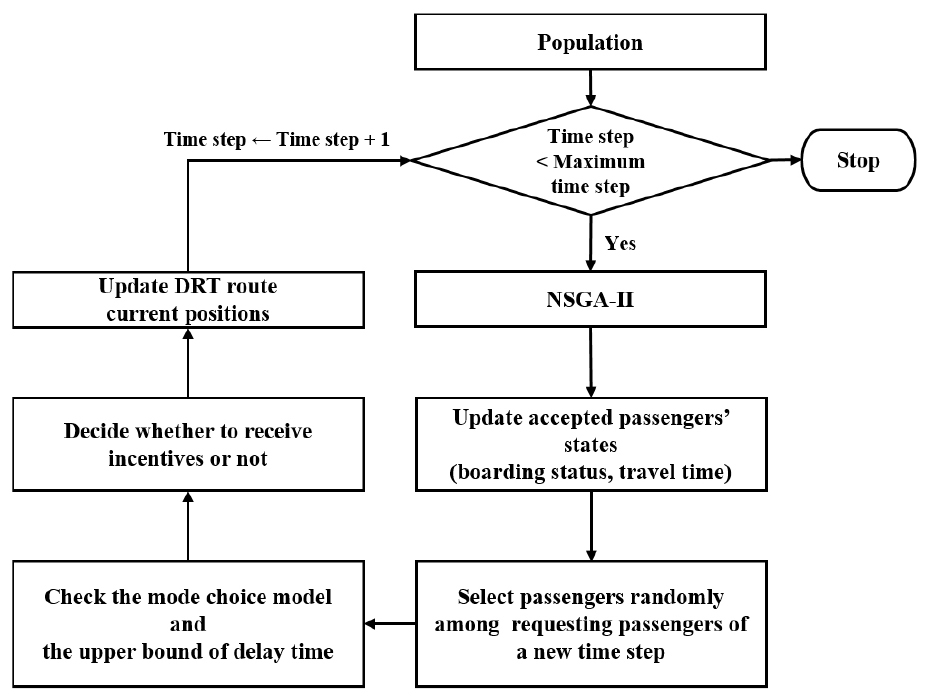
DRT 최적화를 위한 전체 과정은 Figure 2에 나타내었다. 결정 변수는 각 DRT 차량의 승객과 경로이다. 본 연구의 DRT 최적화 과정은 DRT 승객과 경로의 최적 조합을 찾는 조합 최적화 문제이며, 이 문제는 NP-hard 문제이므로 이를 해결하기 위한 휴리스틱 알고리즘이 필요하다. DRT 운영에서는 운영자와 승객의 이해관계가 상충된다. DRT 운영자는 가능한 많은 승객의 요청을 수락하기를 원하지만 승객의 요청이 더 많이 수락되면 DRT 승객 각각의 통행시간이 더 길어지게 된다. 그러나 승객들은 가능한 빨리 목적지에 도착하길 원한다. DRT를 이용할 때 통행시간이 너무 오래 걸리면 승객들은 대중교통과 같은 다른 수단을 이용할 것이다. 따라서 본 연구는 이러한 두 이해당사자를 모두 고려하여 DRT 승객의 총 통행시간을 최소화하고 DRT 운영자의 수입을 최대화하는 다목적 최적화 모델을 설계하였고, 최적화 알고리즘으로는 이에 적합한 Nondominated Sorting Genetic Algorithm-II(NSGA-Ⅱ)를 택했다. NSGA-Ⅱ를 통해 각 DRT 차량의 최적 승객 및 최적 경로를 얻은 후, 예약된 승객의 탑승 상태와 통행 시간이 업데이트된다. 이후 다시 새로 접수된 승객의 요청에 대해 수단 선택 모델이 적용된다. DRT를 이용하려는 승객은 인센티브를 받을지 여부를 결정하고 이를 반영하여 DRT 차량의 경로와 차량의 현재 위치가 업데이트된다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420205/images/kst_2024_422_180_F2.jpg

Figure 2.

Flow chart of process for optimizing DRT

3. 수학적 수식

Table 1은 본 연구의 모델에서 사용된 변수와 그 설명을 보여준다.

Table 1.

The parameters for mathematical formulation

Parameters	Description
$f_{u, v}$	Passenger $u$ ’s fare when using DRT vehicle $v$
$f^{\min}$	Minimum DRT fare
$f^{a d d}$	Additional DRT fee
$d_{u}$	Passenger $u$ ’s Euclidean distance between origin and destination
$d^{\max}$	The maximum distance covered by minimum fare
$x_{u}$	Binary variable to represent whether passenger $u$ ’s travel distance is longer than $d^{\max}$ . If the travel distance is longer than $d^{\max}$ , then $x_{u} = 1$ ; $x_{u} = 0$ otherwise.
$T_{u, v}^{w a i t}$	Passenger $u$ ’s waiting time when using DRT vehicle $v$
$T_{u, v}^{i n v e h}$	Passenger $u$ ’s in-vehicle time when using DRT vehicle $v$
${T_{u, v}}^{w a l k}$	Passenger $u$ ’s walking time when using DRT vehicle $v$
$N$	Fleet size
$y_{u}$	Binary variable to represent whether passenger $u$ is given an incentive. If the passenger is given an incentive, then $y_{u} = 1$ ; $y_{u} = 0$ otherwise
$i n c e n$	Incentive value
$p_{v}^{t}$	Set of passengers who are in the DRT vehicle $v$ at time step $t$
$p_{v}$	Set of passengers who are in the DRT vehicle $v$ on operational period
$C a p$	DRT vehicle’s capacity
$r t_{v}^{t}$	Route of the DRT vehicle $v$ i.e., combinations of boarding and alighting positions of vehicle $v$ ’s passengers at time $t$
$r t_{v}$	Route of the DRT vehicle $v$ i.e., combinations of boarding and alighting positions of vehicle $v$ ’s passengers on operational period
${or}^{i}_{u, v}$	Coordinate of passenger $u$ ’s origin when using vehicle $v$
$d e s_{u, v}$	Coordinate of passenger $u$ ’s destination when using vehicle $v$
$t_{u, v}^{b}$	Passenger $u$ ’s boarding time when using DRT vehicle $v$
$t_{u, v}^{a}$	Passenger $u$ ’s alighting time when using DRT vehicle $v$
$t_{u, v}^{c a l l}$	Passenger $u$ ’s requesting time when using DRT vehicle $v$
$T S$	Time step set
$U B$	Upper bound of delay time
$T_{u, v}^{u p}$	Updated travel time of passenger $u$ when a passenger $u *$ is reserved
$R$	Vehicle’s route set; ${r t_{1}, r t_{2}, \dots, r t_{n}}$
$P$	Set of vehicle’s passenger set; ${p_{1}, p_{2}, \dots, p_{n}}$ on operational period

본 연구에서의 DRT 요금 체계는 승객들의 예약 시점에 안내된 출발지와 목적지 사이의 거리 기반으로 Equation 1과 같이 계산된다.

(1)

f_{u, v} = f^{\min} + x_{u} \times (f^{a d d} \times ⌊ d_{u} - d^{\max} ⌋)

여기서 $⌊ k ⌋$ 는 $k$ 보다 작거나 같은 가장 큰 정수를 나타낸다.

운영자 관점에서의 수입 극대화와 이용자 관점에서의 총 통행시간 최소화라는 목적을 가진 다목적 혼합 정수 비선형 프로그래밍(multi-objective mixed-integer nonlinear programming; 다목적 MINLP) 모델은 Equations 2, 3, 4, 5, 6, 7, 8, 9와 같다. 일부 승객에게 인센티브가 제공된 경우 운영자의 수입에서 인센티브만큼 차감한다. 인센티브를 받는 승객은 탑승 지점까지 도보로 이동한다고 가정하였다. 따라서 DRT 승객의 총 이동 시간은 도보시간, 대기시간 및 차내시간의 합으로 계산된다.

(2)

\{\begin{cases} \max \sum_{v = 1}^{N} \sum_{u \in p_{v}} (f_{u, v} - y_{n} \times i n c e n) \\ \min \sum_{v = 1}^{N} \sum_{u \in p_{v}} (y_{u} \times {T_{u, v}}^{w a l k} + {T_{u, v}}^{w a i t} + {T_{u, v}}^{i n v e h} \end{cases}

subject to

(3)

\forall t, v, | p_{v}^{t} | \leq C a p

(4)

\forall u, v, or i_{u, v} \in r t_{v}, d e s_{u, v} \in r t_{v}

(5)

\forall v, v', v \neq v', p_{v} \cap p_{v'} = \emptyset

(6)

t_{u, b}^{b} \in T S, t_{u, v}^{a} \in T S

(7)

t_{u, v}^{b} < t_{u, v}^{a}

(8)

\forall u \in p_{v}^{t}, \exists u * \in p_{v}^{t + 1} s . t . T_{u, u *}^{u p} < U B

(9)

\forall u, v, T_{u, v}^{w a l k} + T_{u, v}^{w a i t} = t_{u, v}^{b} - t_{u, b}^{c a l l}

Equation 3은 탑승 가능한 총 승객 수가 DRT 차량 정원보다 작거나 같아야 함을 의미한다. Equation 4는 경로가 출발지와 목적지의 조합으로 이루어진다는 것을 나타낸다. Equation 5는 서로 다른 차량이 동시에 동일한 승객을 수용할 수 없음을 나타낸다. Equation 6은 탑승 및 하차가 time step 집합의 요소임을 나타낸다. Equation 7은 각 승객이 탑승 후 하차함을 나타낸다. Equation 8는 최대 지연시간 제약 조건이다. Equation 9는 요청부터 탑승까지의 시간이 도보시간과 대기시간의 합과 같음을 의미한다. 이때 도보시간은 인센티브를 받지 않은 승객에게는 0이 된다.

결정 변수는 각 차량의 경로와 승객으로 Equation 10, 11과 같이 표현된다.

(10)

R = {r t_{1}, r t_{2} \dots, r t_{n}}

(11)

P = {p_{1}, p_{2}, \dots, p_{n}}

4. DRT와 대중교통 간 수단선택 모델

본 연구의 문제 정의에 따라 승객들은 평균 차내시간, 평균 대기시간, 도보시간 및 요금을 기반으로 DRT와 대중교통을 비교하고 경제적이고 효율적인 수단를 선택한다. 본 연구에서는 정해진 노선이 있는 대중교통과 정해진 노선이 없는 DRT 사이의 수단선택모형(Chavis et al., 2017)을 채택하였다. Chavis et al.(2017)의 수단선택모형에 사용된 변수는 Table 2, 파라미터의 값은 Table 3과 같으며, 본 연구에도 동일하게 적용하였으며, 비용의 경우 단위를 국내 단위로 환산하여 적용하였다.

Table 2.

The parameters utilized in the mode choice model

Parameters	Description
$d e l_{u}^{\exp}$	Passenger $u$ ’s average delay time compared to expected travel time
$T_{u, v}^{\exp (i n v e h)}$	Passenger $u$ ’s expected in-vehicle time when requesting vehicle $v$
$\bar{T_{u, v}^{i n v e h}}$	Passenger $u$ ’s average in-vehicle time when using vehicle $v$
$T_{u, v}^{\exp (w a i t)}$	Passenger $u$ ’s expected waiting time when requesting vehicle $v$
$T_{u, v}^{w a i t}$	Passenger $u$ ’s average waiting time when using vehicle $v$
$T_{u, v}^{w a l k}$	Passenger $u$ ’s walking time to board the vehicle $v$
$C_{u, v}$	Fare payed by a passenger $u$ when using vehicle $v$
$U_{u} (r t_{v}^{t})$	Passenger $u$ ’s utility when requesting DRT vehicle $v$ at time step $t$ , which is influenced by the route of the DRT vehicle
$α_{j}$	The alternative specific constant of mode $j$ (DRT or public transportation)
$β_{j}$	The explanatory variable’s coefficient

Table 3.

The value of $α_{j}$ and $β_{j}$ (Chavis et al.(2017))

Category	Coefficient $β_{j}$	p-value
Alternative specific constant $α_{j}$
Fixed route transit	0.00	Fixed
Flexible route transit	-0.937	.00*
Explanatory variables, $β_{j}$
$C_{u, v} (K R W)$	-0.0630	.00*
$T_{u, v}^{i n v e h} (\min)$	-0.0205	.01*
$T_{u, v}^{w a i t} (\min)$	-0.0109	.00*
$T_{u, v}^{w a l k} (\min)$	-0.0472	.00*

*significance at the 95% confidence interval

승객이 DRT를 요청할 때, DRT 운영자는 DRT 차량의 현재 경로를 기반으로 승객에게 예상 차내시간, 예상 대기시간, 최대 지연시간이 각각 몇 분인지를 고지한다. 차내시간 및 대기시간은 최대 지연시간 이상으로 증가하지는 않는다. Equation 12에서 지연 시간 기댓값( $d e l_{u}^{\exp}$ )은 최대 지연시간의 절반으로 가정한다. 또한, 예상 지연시간 중 차내시간의 증가량과 대기시간의 증가량이 차지하는 비중이 동일하다고 가정하며, 이에 따라 차내시간 기댓값과 대기시간 기댓값은 각각 Equation 13, 14와 같이 계산된다. 이와 같이 계산된 차내시간 및 대기시간 기댓값과 요금, 도보시간을 적용하여 각 수단별 효용함수를 계산할 수 있다(Equation 15).

(12)

d e l_{u}^{\exp} = \frac{U B}{2}

(13)

T_{u, v}^{i n v e h} = T_{u, v}^{\exp (i n v e h)} + \frac{d e l_{u}^{e x p}}{2}

(14)

T_{u, v}^{w a i t} = T_{u, v}^{\exp (w a i t)} + \frac{d e l_{u}^{\exp}}{2}

(15)

U_{u} (r t_{v}^{t}) = α_{j} + β_{1} C_{u, v} + β_{2} T_{u, v}^{i n v e h} + β_{3} T_{u, v}^{w a i t} + β_{4} T_{u, v}^{w a l k}

수단 선택 모델은 Equation 16, 17에 표현된 로짓 모델을 사용하여 각 수단의 효용함수를 기반으로 적용된다. 한 번 요청이 수락되면 승객은 인센티브를 받을지 여부를 결정하고, 인센티브를 받기로 결정한 승객은 인근 DRT 탑승 지점까지 걸어간다. 이 경우 해당 승객이 DRT를 이용할 때의 차내시간, 대기시간, 요금, 도보시간이 변하므로 효용함수 역시 달라진다.

(16)

\Pr_{D R T} (u) = \frac{e^{U_{u}^{D R T} (r t_{v}^{t})}}{e^{U_{u}^{D R T} (r t_{v}^{t})} + e^{U_{u}^{D R T - i n c n} (r t_{v}^{t})} + e^{U_{u}^{P T} (r t_{v}^{t})}}

(17)

\Pr_{D R T - i n c n} (u) = \frac{e^{U_{u}^{D R T - i n c n} (r t_{v}^{t})}}{e^{U_{u}^{D R T} (r t_{v}^{t})} + e^{U_{u}^{D R T - i n c n} (r t_{v}^{t})} + e^{U_{u}^{P T} (r t_{v}^{t})}}

여기서 $\Pr_{D R T} (u)$ 은 승객 $u$ 가 인센티브를 받지 않는 DRT를 선택할 확률을, $\Pr_{D R T - i n c n} (u)$ 승객 $u$ 가 인센티브를 받는 DRT를 선택할 확률을 나타낸다. $U_{u}^{D R T} (*)$ 는 인센티브를 받지 않는 DRT의 효용함수, $U_{u}^{D R T - i n c n} (*)$ 는 인센티브를 받는 DRT의 효용함수, $U_{u}^{P T} (*)$ 는 대중교통의 효용함수를 나타낸다.

사례 연구

본 연구는 인천광역시(Figure 3)를 대상으로 DRT 최적화 및 인센티브 전략을 적용하였다. 인천광역시는 인천국제공항, 상업지구, 해변 등 다양한 시설을 보유하고 있어 다양한 통행이 발생하기 때문에 해당 도시를 사례 연구의 네트워크로 채택했다. 대중교통 정류장의 위치는 GIS 데이터에서 얻었다. 본 연구에서는 택시와 DRT가 이용자들의 출발지와 도착지를 환승 없이 연결시켜주는 공통점이 있다는 점을 고려하여, 택시 이용 데이터가 DRT의 잠재적인 수요를 나타낸다고 간주하고 이를 이용하였다. Taxi operation information management system(TIMS) 데이터는 승객의 정보를 제공하며, 승차 좌표, 하차 좌표, 승차 시간 및 하차 시간과 같은 정보가 포함되어 있다. 본 연구에서는 2018년 11월 13일 오후 6시부터 8시까지의 택시 이용 데이터를 사용했으며, 총 16,698명의 승객이 평균 12.8분 동안 4.2km를 통행했다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420205/images/kst_2024_422_180_F3.jpg

Figure 3.

The spatial scope of the case study

연구 결과

인센티브를 받는 DRT 승객은 도보로 승차 지점까지 이동해야 하므로, DRT 승객은 걸어가는 거리와 요금을 고려하여 인센티브를 받을지 여부를 결정한다. 높은 인센티브 전략은 많은 승객을 유인할 수 있지만, DRT 운영자의 수입이 감소한다. 또한 승객 수가 증가하면 DRT 차량은 DRT 승객을 승차 및 하차시키기 위해 더 많은 우회를 하게 되어 DRT 서비스의 질이 저하된다. 이러한 이유로 DRT 운영에 적절한 인센티브 값을 결정하는 것이 중요하다. 본 연구에서는 인센티브 값을 50원에서 250원까지 50원 간격으로 변경하여 민감도 분석을 실시했다. DRT 차량의 속도는 30km/h로 일정하다고 가정하였으며, DRT 요금은 현대자동차가 2019년 인천광역시 영종도에서 시행한 DRT 시범 프로젝트인 I-MOD에서 사용한 요금과 같게 설정하였다. 5km 미만 이동 승객은 기본 요금인 1,250원의 요금을 지불하며, 5km 이상 이동 승객은 1km당 100원의 추가 요금을 지불하게 된다. 또한, 최대 지연시간 비율은 50%로 가정하였다.

1. 승객 수와 도보 시간

본 연구의 목적 중 하나는 수입을 극대화하는 것이기 때문에, 인센티브 값이 증가함에 따라 전체 승객 수와 인센티브를 받는 승객 수 둘 다 증가하다가 어느 시점부터 감소하기 시작하는데, 이 점은 Table 4와 Figure 4에서 확인할 수 있다. 인센티브를 받는 승객 수가 감소하기 시작하는 지점은 DRT 기본 요금인 1,250원의 12%인 150원 지점이다.

Table 4.

The number of passengers and total walking time

Incentive (KRW)	50	100	150	200	250
The number of passengers who receive incentives	3-8	18-21	21-23	8-11	3-5
The number of passengers	131-151	163-177	164-175	132-147	126-134
Total walking time (min)	4.6-17.8	29.5-33.8	47.5-49.7	19.1-37.6	16.4-25.0

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420205/images/kst_2024_422_180_F4.jpg

Figure 4.

The number of passengers by the incentive value; (a) total number of passengers and (b) number of passengers who receive incentives

인센티브를 받는 DRT 승객은 다른 승객의 승하차 지점까지 이동함으로써 DRT 차량이 추가적으로 우회하지 않도록 하며, 이는 최대 지연시간 제약조건을 위반하지 않고 더 많은 승객 요청을 수락할 수 있게 한다. 이로 인해 인센티브가 50-150원일 때는 인센티브가 증가하면 인센티브를 받는 승객 수와 전체 승객 수가 모두 증가한다. 그러나 인센티브가 150원을 넘어서면 승객 수가 감소하는데, 이는 인센티브가 높을 때는 운영자가 인센티브를 받는 승객을 수락하게 되면 수입이 감소하므로, 인센티브를 받는 승객을 제외하려 하기 때문이다. 인센티브를 받는 승객의 비율이 낮아지면 DRT 차량의 우회가 증가하므로, 최대 지연시간 제약조건을 위반하지 않고 수락할 수 있는 전체 승객의 수도 줄어든다.

총 도보 시간은 인센티브를 받는 승객 수와 동일한 패턴을 나타내어, 인센티브가 50-150원일 때는 증가하고 150원을 넘어서면 감소하는 것으로 나타났다.

2. 평균 통행시간과 평균 수입

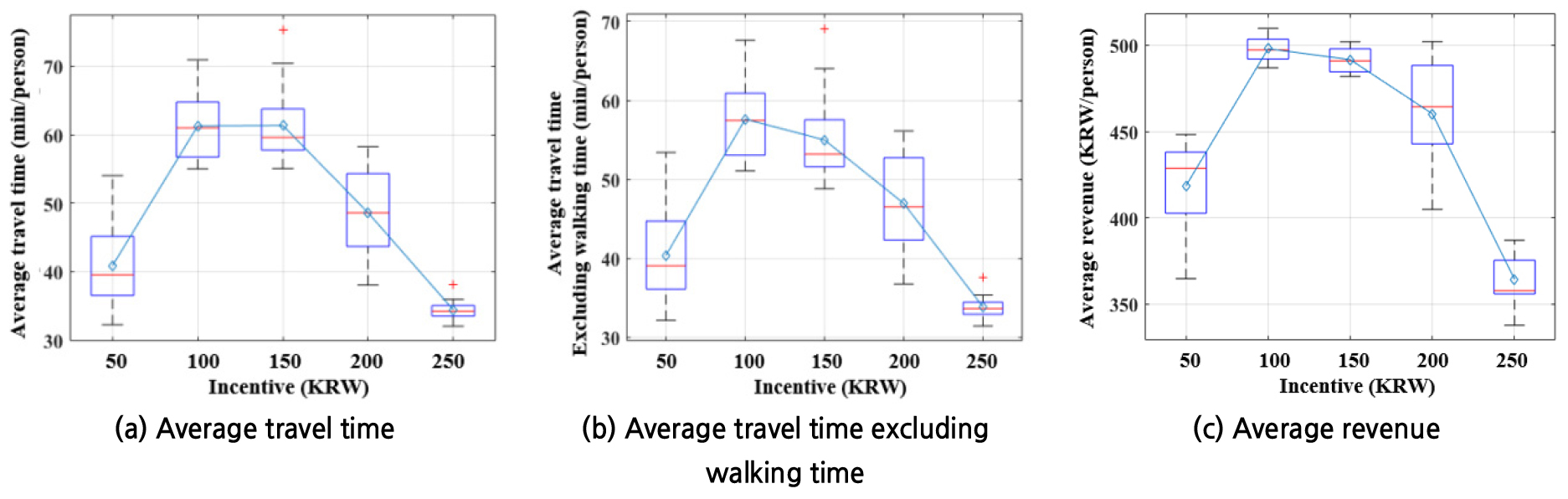
인센티브가 50-150원일 때는 인센티브가 증가함에 따라 평균 통행시간도 증가하다가, 인센티브가 150원을 넘어서면 평균 통행시간이 감소한다(Table 5, Figure 5(a)). 또한, 도보를 제외한 평균 통행시간(대기 및 차내시간)은 인센티브가 50-100원일 때는 인센티브가 증가함에 따라 같이 증가하다가, 인센티브가 100원을 넘어서면 감소한다(Figure 5(b)). 감소의 시작점이 150원에서 100원으로 변경되었지만, 도보를 제외한 평균 통행시간의 변화 패턴은 평균 통행시간과 거의 동일하다. 이 사실은 도보 통행시간이 평균 통행시간의 증가와 감소에 중요한 영향을 미치지 않음을 나타낸다.

Table 5.

Average travel time and average revenue

Incentive (KRW)	50	100	150	200	250
Average travel time (min/person)	32.3-54.0	55.0-70.9	55.1-75.4	38.1-58.3	32.0-38.2
Average travel time excluding walking time (min/person)	32.2-53.4	51.1-67.6	48.8-69.1	36.8-56.1	31.4-37.6
Average revenue (KRW/person)	359-449	490-511	481-501	402-502	339-386

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420205/images/kst_2024_422_180_F5.jpg

Figure 5.

Average travel time and revenue; (a) average travel time, (b) average travel time excluding walking time, and (c) average revenue

평균 통행시간은 인센티브 값이 150원이 될 때까지 증가한다. 이는 인센티브가 50-150원일 때는 통행시간이 긴 요청을 수락하더라도 최대 지연시간 제약 조건을 위반하지 않는다는 것을 의미한다. 앞서 인센티브가 50-150원일 때는 인센티브가 증가할 때 인센티브를 받는 승객 수가 증가한다는 결과가 나타났다. 인센티브를 받는 승객의 비율이 높아지면 DRT 차량의 우회가 감소하므로, 최대 지연시간 제약 조건을 위반하지 않고 더 긴 통행시간을 갖는 요청을 수락할 수 있는 것이다. 반대로 인센티브가 150원을 넘어서면 평균 통행시간이 감소하는 것은, 인센티브를 받는 승객 수가 감소하고, 인센티브를 받는 승객의 비율이 낮아지면 DRT 차량의 우회가 증가하므로, 최대 지연시간 제약 조건을 위반하지 않고 더 긴 통행시간을 갖는 요청을 수락하기 어려워지는 것이다. 반면, 평균 수입은 인센티브 값이 기본 요금인 1,250원의 8%인 100원이 될 때까지 증가하다 100원 이후부터 감소한다.

3. Pareto-optimal set

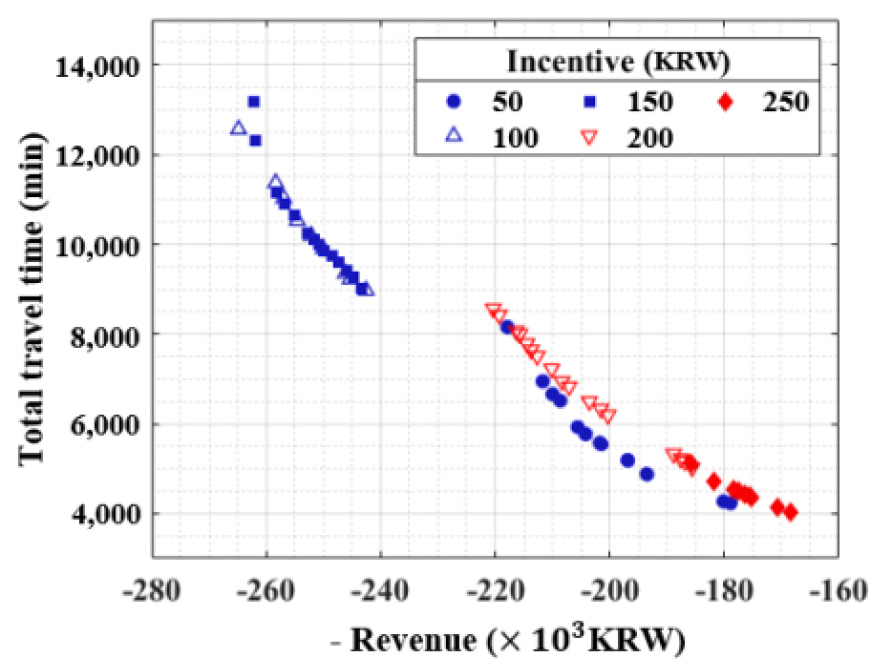
NSGA-II를 이용하여 구한 총통행시간과 총수입의 최적 조합은 Pareto-optimal set으로 나타난다(Table 6, Figure 6). 앞서 인센티브가 150원을 넘어서면 DRT 운영자가 인센티브를 받는 요청을 수락하지 않으려 하며, 이로 인해 승객 수, 평균 통행시간 및 평균 수입이 감소하는 것으로 나타났다. 이로 인해 인센티브가 200-250원일 때는 50-150원일 때보다 Pareto-optimal set 측면에서 열등한 것으로 나타났다. 인센티브 값이 50원일 때도 수입과 총 통행시간 모두 인센티브 값이 100-150원일 때보다 낮으며, 이는 DRT 운영자에게 적합하지 않다. 인센티브 값이 100원일 때와 150원일 때는 수입과 총 통행시간이 비슷하지만, 수입이 260,000원이고 총 이동 시간이 11,000분인 지점 근방에서는 인센티브 값이 100원인 경우가 인센티브 값이 150원인 경우보다 우세하다.

Table 6.

Revenue and total travel time

Incentive (KRW)	50	100	150	200	250
Revenue (KRW)	178,900-217,900	242,600-264,900	243,500-262,300	185,600-220,400	168,600-185,700
Total travel time (min)	4,229-8,158	8,967-12,557	9,082-13,188	5,026-8,563	4,037-5,114

https://cdn.apub.kr/journalsite/sites/kst/2024-042-02/N0210420205/images/kst_2024_422_180_F6.jpg

Figure 6.

Pareto optimal set for each incentive value

4. 제언

DRT 승객 및 운영자는 서로 상충되는 이해관계를 갖고 있으며, DRT의 성공적인 운영을 위해서는 양쪽 이해당사자의 요구에 모두 부응하는 균형잡힌 전략을 적용해야 한다. 인센티브 시스템은 DRT 운영자와 DRT 승객 양쪽에 만족스러운 서비스를 제공하기 위해 적용될 수 있다. 그러나 본 연구에서는 인센티브 값이 너무 높을 경우 운영자의 수입을 감소시켜 인센티브를 받는 요청을 수락하지 않게 할 수 있음을 발견하였다. 따라서 적절한 인센티브 값을 결정하는 것은 효율적인 DRT 운영에 중요하다. 본 연구에서는 인천광역시의 택시 데이터가 DRT의 잠재적인 수요를 나타낸다고 간주하고 최적의 인센티브를 산정한 결과, 인센티브 값이 DRT 기본 요금의 12%로 설정될 때 승객 수가 가장 높게 나타났으며, 이동시간이 긴 요청도 쉽게 수락되었다. 한편, DRT 기본 요금의 8%로 인센티브 값이 설정될 때 평균 수입이 가장 높게 나타났다. 다만 DRT 서비스를 실제로 운영한다면 운영하고자 하는 지역의 수요 패턴을 분석하여 적절한 인센티브 값을 적용해야 할 것이다.

결론

대중교통을 이용하는 승객들은 first-mile 및 last-mile 문제를 겪게 되며, DRT는 승객을 출발지에서 태우고 목적지에서 내려주는 door-to-door 서비스로 이런 문제를 해결할 수 있다. 본 연구에서는 다른 승객의 승하차 지점으로 이동하는 승객에게 인센티브가 제공되는 전략을 제안하였다. DRT와 대중교통 중 대중교통을 선택하게 되는 가장 큰 이유는 DRT 차량의 우회로 인해 통행시간이 증가하기 때문이다. 승객이 다른 승객의 승하차 지점으로 이동한다면, DRT 차량은 승객을 태우기 위해 추가적인 우회 및 통행시간 증가가 발생하지 않게 된다. 인센티브 시스템이 인센티브를 제공함으로써 수입에 부정적인 영향을 미칠 수 있지만, 적절한 인센티브를 제공하면 더 많은 승객이 DRT를 이용하게 되어 더 큰 수입을 얻을 수 있다. 본 연구에서는 지나친 통행시간 증가를 방지하기 위해 최대 지연시간을 설정하였다. 본 연구에서는 동적 승객 요청을 기반으로 총 통행시간을 최소화하고 수입을 극대화하기 위한 다중 목적 MINLP를 이용하여 인센티브 시스템을 갖춘 동적 DRT를 설계하였다. 각 차량별 경로와 승객을 나타내는 최상의 결정 변수를 찾기 위해 조합 최적화를 수행하였고, 이는 NP-hard 문제로 알려져 있으므로 이 문제를 해결하기 위해 NSGA-Ⅱ를 사용하였다. 사례 연구는 TIMS 데이터를 사용하여 인천광역시를 대상으로 수행되었다. 인센티브 값을 50원에서 250원까지 50원 간격으로 변경함으로써 DRT 승객 및 DRT 운영자 모두에게 적절한 인센티브 값을 찾기 위한 민감도 분석을 수행하였다.

인센티브가 증가하면 DRT 승객들은 인센티브를 받고 DRT를 이용할 가능성이 높아진다. 이에 따라 본 연구의 결과에서는 인센티브 값이 50원에서 150원으로 증가함에 따라 승객 수가 증가하는 것을 살펴볼 수 있었다. 그러나 너무 높은 인센티브는 DRT 업체의 수입을 낮추기 때문에 인센티브 값이 어느 지점을 넘어서면 인센티브를 받는 승객의 수가 감소하며, 본 연구의 경우 그 지점이 DRT 기본요금의 12%(150원)로 나타났다. 이는 DRT 운영자가 인센티브를 받기 위해 걸어가기로 결정한 요청을 거절하기 때문에 승객 수가 줄어들게 되는 것이다.

평균 수입은 인센티브 값이 100원일 때 가장 높은 반면, 인센티브를 받는 승객 수는 인센티브가 150원일 때 가장 많다. 인센티브가 150원을 넘어서면 승객 수와 평균 통행시간이 감소하며, 이에 따라 평균 수입도 감소한다. 각 인센티브 값에 대한 Pareto-optimal set에서 인센티브 값이 200-250원일 때는 다른 경우에 비해 열등한 것으로 나타났다. 본 연구의 데이터에서는 DRT 기본요금의 12%(150원)로 인센티브 값을 설정하면 승객 수와 평균 통행시간이 가장 컸고, DRT 기본요금의 8%(100원)로 인센티브 값을 설정하면 가장 높은 수입을 얻을 수 있음을 발견하였으나, 실제 서비스 운영 시에는 수요 패턴에 따라 인센티브 값을 조정할 필요가 있다.

본 연구에서는 DRT의 경쟁수단으로 대중교통만을 고려하였으나, 향후 연구에서는 자가용 등 다른 수단도 경쟁수단으로 고려할 수 있다. 또한, 본 연구에서는 최대 지연시간 비율을 50%로 설정하였으나 DRT 이용 데이터가 확보된다면 이를 바탕으로 실제 수요패턴에 부합하는 최대 지연시간 비율을 설정할 수 있을 것이다. 한편 본 연구에서 사용한 DRT 수단선택모형은 국내와 다른 환경에 대해서 구축된 것이며, 향후 연구에서는 국내 환경에 적합한 수단선택모형을 구축하고 이를 기반으로 DRT 인센티브 전략을 수립할 필요가 있다. 그리고 본 연구에서는 대중교통과 DRT가 경쟁하여 이용자가 둘 사이에서 수단선택을 하는 상황을 전제하였으나, 우리나라에서는 현재까지 DRT가 주로 대중교통 서비스가 부족한 교통소외지역에서 운영되고 있으므로 본 연구의 결과를 DRT 운영에 그대로 적용하기는 어려운 점이 있다. 교통소외지역에서의 경우 승용차, 택시 등 다른 수단을 고려한 수단선택모형을 구축하여 이를 기반으로 인센티브 전략을 수립하는 것이 바람직할 것이다. 또한, 최근에는 도시 지역에서의 대중교통 불편을 해결하기 위한 DRT 도입 사례가 늘어나고 있으며, 이러한 경우에 대해서는 본 연구의 방법론을 기반으로 인센티브 전략을 수립하기 적합할 것이다.

Funding

This work was supported by National Research Foundation of Korea(NRF) grant funded by the Korea Government(MSIT) (No.2022R1A2C2012835). This research was also supported by the BK21 PLUS research program of NRF.

References

Amirgholy M., Gonzales E. J. (2016), Demand Responsive Transit Systems with Time-dependent Demand: User Equilibrium, System Optimum, and Management Strategy, Transportation Research Part B: Methodological, 92, 234-252.

10.1016/j.trb.2015.11.006

Asensio J. (2002), Transport Mode Choice by Commuters to Barcelona's CBD, Urban Studies, 39(10), 1881-1895.

10.1080/0042098022000003000

Buehler R. (2011), Determinants of Transport Mode Choice: A Comparison of Germany and the USA, Journal of transport geography, 19(4), 644-657.

10.1016/j.jtrangeo.2010.07.005

Chavis C., Gayah V. V. (2017), Development of a Mode Choice Model for General Purpose Flexible-route Transit Systems, Transportation Research Record, 2650(1), 133-141.

10.3141/2650-16

Chen J., Li S. (2017), Mode Choice Model for Public Transport with Categorized Latent Variables, Mathematical Problems in Engineering.

10.1155/2017/7861945

Chevrier R., Liefooghe A., Jourdan L., Dhaenens C. (2012), Solving a Dial-a-ride Problem with a Hybrid Evolutionary Multi-objective Approach: Application to Demand Responsive Transport, Applied Soft Computing, 12(4), 1247-1258.

10.1016/j.asoc.2011.12.014

Dessouky M., Rahimi M., Weidner M. (2003), Jointly Optimizing Cost, Service, and Environmental Performance in Demand-responsive Transit Scheduling, Transportation Research Part D: Transport and Environment, 8(6), 433-465.

10.1016/S1361-9209(03)00043-9

Diana M., Quadrifoglio L., Pronello C. (2007), Emissions of Demand Responsive Services as an Alternative to Conventional Transit Systems, Transportation Research Part D: Transport and Environment, 12(3), 183-188.

10.1016/j.trd.2007.01.009

Diana M., Dessouky M. M., Xia N. (2006), A Model for the Fleet Sizing of Demand Responsive Transportation Services with Time Windows, Transportation Research Part B: Methodological, 40(8), 651-666.

10.1016/j.trb.2005.09.005

Guo R., Guan W., Zhang W., Meng F., Zhang Z. (2019), Customized Bus Routing Problem with Time Window Restrictions: Model and Case Study, Transportmetrica A: Transport Science, 15(2), 1804-1824.

10.1080/23249935.2019.1644566

Guo R., Guan W., Zhang W. (2018), Route Design Problem of Customized Buses: Mixed Integer Programming Model and Case Study, Journal of Transportation Engineering, Part A: Systems, 144(11), 04018069.

10.1061/JTEPBS.0000185

Hensher D. A., Li Z., Leung W., Rose J. (2012), Choosing Public Transport-some Behavioural Challenges, In International Conference on Advanced Systems for Public Transport.

Jaw J. J., Odoni A. R., Psaraftis H. N., Wilson N. H. (1986), A Heuristic Algorithm for the Multi-vehicle Advance Request Dial-a-ride Problem with Time Windows, Transportation Research Part B: Methodological, 20(3), 243-257.

10.1016/0191-2615(86)90020-2

Lyu Y., Chow C. Y., Lee V. C., Ng J. K., Li Y., Zeng J. (2019), CB-Planner: A Bus Line Planning Framework for Customized Bus Systems, Transportation Research Part C: Emerging Technologies, 101, 233-253.

10.1016/j.trc.2019.02.006

Lyu Y., Chow C. Y., Lee V. C., Li Y., Zeng J. (2016), T2CBS: Mining Taxi Trajectories for Customized Bus Systems, In 2016 IEEE Conference on Computer Communications Workshops (INFOCOM WKSHPS), 441-446, IEEE.

Nourbakhsh S. M., Ouyang Y. (2012), A Structured Flexible Transit System for Low Demand Areas, Transportation Research Part B: Methodological, 46(1), 204-216.

10.1016/j.trb.2011.07.014

Palmer K., Dessouky M., Abdelmaguid T. (2004), Impacts of Management Practices and Advanced Technologies on Demand Responsive Transit Systems, Transportation Research Part A: Policy and Practice, 38(7), 495-509.

10.1016/j.tra.2004.05.002

Papanikolaou A., Basbas S., Mintsis G., Taxiltaris C. (2017), A Methodological Framework for Assessing the Success of Demand Responsive Transport (DRT) Services, Transportation Research Procedia, 24, 393-400.

10.1016/j.trpro.2017.05.095

Quadrifoglio L., Shen C. W. (2009), Performance Analysis of the "Zoning" Strategies for ADA Paratransit Services, Southwest Region University Transportation Center, Texas Transportation Institute, Texas A & M University System.

Quadrifoglio L., Dessouky M. M., Ordóñez F. (2008), A Simulation Study of Demand Responsive Transit System Design, Transportation Research Part A: Policy and Practice, 42(4), 718-737.

10.1016/j.tra.2008.01.018

Shen C. W., Quadrifoglio L. (2012), Evaluation of Zoning Design with Transfers for Paratransit Services, Transportation Research Record, 2277(1), 82-89.

10.3141/2277-10

Shen C. W., Quadrifoglio L. (2011), The Coordinated Decentralized Paratransit System: Formulation and Comparison with Alternative Strategies, 11-2825.

Vuchic V. R. (2007), Urban Transit Systems and Technology, John Wiley & Sons.

10.1002/9780470168066

Wang C., Ma C., Xu X. D. (2020), Multi-objective Optimization of Real-time Customized Bus Routes Based on Two-stage Method, Physica A: Statistical Mechanics and its Applications, 537, 122774.

10.1016/j.physa.2019.122774

Wong K. I., Han A. F., Yuen C. W. (2014), On Dynamic Demand Responsive Transport Services with Degree of Dynamism, Transportmetrica A: Transport Science, 10(1), 55-73.

10.1080/18128602.2012.694491

Journal of Korean Society of Transportation 대한교통학회지 ISSN:1229-1366(Print) 2234-4217(Online)

Preview

Incentive Strategy to Improve Passenger Convenience and Operation Efficiency of Demand-Responsive Transportation Systems

ABSTRACT

MAIN

Figure 1.

Examples of how DRT is operated in each time step

Figure 2.

Flow chart of process for optimizing DRT

Table 1.

The parameters for mathematical formulation

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

Table 2.

The parameters utilized in the mode choice model

Table 3.

The value of αj and βj (Chavis et al.(2017))

(12)

(13)

(14)

(15)

(16)

(17)

Figure 3.

The spatial scope of the case study

Table 4.

The number of passengers and total walking time

Figure 4.

The number of passengers by the incentive value; (a) total number of passengers and (b) number of passengers who receive incentives

Table 5.

Average travel time and average revenue

Figure 5.

Average travel time and revenue; (a) average travel time, (b) average travel time excluding walking time, and (c) average revenue

Table 6.

Revenue and total travel time

Figure 6.

Pareto optimal set for each incentive value

Funding

References

The value of $α_{j}$ and $β_{j}$ (Chavis et al.(2017))