Multi-Stage Machine Learning Approach to Assess Crash Risk Using Vehicle Maneuver Data

Nuri Park; Juneyoung Park

doi:10.7470/jkst.2024.42.3.331

Preview

Article

Journal of Korean Society of Transportation. 30 June 2024. 331-347
https://doi.org/10.7470/jkst.2024.42.3.331

Multi-Stage Machine Learning Approach to Assess Crash Risk Using Vehicle Maneuver Data

차량 주행궤적 데이터를 활용한 Multi-Stage 머신러닝 기반의 사고 위험 예측 연구

Nuri PARK¹

Juneyoung PARK²^*

박 누리¹

박 준영²^*

¹Ph.D. Student, Department of Smart City Engineering, Hanyang University, Ansan 1558, Korea

²Associate Professor, Department of Transportation & Logistics Engineering/Smart City Engineering, Hanyang University, Ansan 15588, Korea

¹한양대학교 스마트시티공학과 박사과정

²한양대학교 교통·물류공학과/스마트시티공학과 부교수

^{*Corresponding Author}

License (open-access, http://creativecommons.org/licenses/by-nc/3.0/):

This is an Open-Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0) which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

ABSTRACT

The selection of indicators that can catch the risky traffic flow is important to predict crash risk on highways. Unsupervised machine learning techniques can be a new approach to deriving important crash risk indicators. This paper applies a multi-stage methodology using both unsupervised and supervised machine learning techniques systematically to evaluate crash risks. The proposed multi-stage methodology is composed of three stages. In the first stage, select variables that can classify risky and general traffic flow well using K-means clustering and Random forest. The second stage is the combination of variables that were derived in the first stage to construct important variable sets for detecting crash precursors. Lastly, third stage, crash prediction models with variable sets, which are selected from the second step, were developed using the support vector machine method. For the real-time crash prediction model, individual vehicle trajectory data were collected from commercial vehicles and used. As a result of this study, the multi-stage models that include variable selection through a combination of K-means clustering and Random Forest methods improved the predictive performance. This study proposes a new approach to selecting important variables that cannot be found by supervised learning when developing a crash prediction model. It is expected that more crashes can be prevented by performing proactive traffic safety management using the methodology suggested in this study.

Keywords

crash precursor

crash risk

machine learning

multi-stage model

safety indicators

교통사고 발생 예방과 대응을 위하여 실시간으로 사고위험 상황을 예측하고 적절한 조처를 하는 방안에 관한 연구가 진행되고 있다. 교통사고는 매우 드물게 발생하는 무작위 이벤트이기 때문에 실시간 사고 위험 예측에서 사고 발생 징후를 포착하고 위험한 교통류 특성을 명확히 구분할 수 있는 안전 지표를 선택하는 것이 중요하다. 본 연구에서는 머신러닝 기법 중 비지도 학습과 지도학습 방법론을 동시에 활용하여 중요도 높은 핵심 안전 지표를 선별하였으며, 선정된 안전 지표를 활용해 사고위험 예측모형을 개발하는 Multi-stage process의 사고 위험 예측 모형 개발 절차를 제안하였다. 첫 번째 단계에서는 K-means Clustering과 Random Forest 방법론을 사용하여 사고위험 교통류와 일반 교통류를 잘 분류할 수 있는 변수를 선별하였으며, 두 번째 단계에서는 첫 번째 단계에서 도출된 핵심 변수의 조합을 마련하였다. 마지막으로 세 번째 단계에서는 이진 분류에 많이 사용되는 머신러닝 기법인 Support Vector Machine 모형을 사용해 변수 조합별 사고 위험 예측 모형을 개발하고, 예측 성능을 비교하였다. 이를 통해 본 연구에서는 사고위험 예측모형에 독립변수로 활용되는 안전 지표를 선별할 때 비지도 학습 및 지도 학습 기반 핵심 변수 선별 방법론의 효과를 측정하였다. 또한, 본 연구에서는 실시간으로 변화하는 차량의 위험 주행행태 포착을 위해 상업용 차량의 Digital Tachograph(DTG)에서 수집되는 주행궤적 데이터를 사용하였다. 연구 결과, 본 연구에서 제안한 Multi-stage 기반 사고 위험 예측 모형 개발 방식은 모형의 예측 성능을 개선하는 것으로 나타났으며, 핵심 변수 선별에 지도학습만으로는 도출되지 않는 새로운 중요한 변수를 고려할 수 있는 것으로 나타났다. 본 연구에서 제안된 방법론을 사용하여 선제적 교통안전 관리 전략을 마련할 수 있으며, 이를 통해 교통사고를 예방하고, 교통안전 관리 전략을 통해 사전에 대응할 수 있을 것으로 기대한다.

키워드

사고 발생 징후

사고위험

머신러닝

multi-stage 모형

안전 지표

MAIN

서론
선행연구
연구방법론
1. 변수 중요도 도출
2. 사고위험 예측모형
3. 모형성능평가
자료수집
분석 결과
1. First-stage; 변수 선택
2. Second-stage; 변수 조합 생성
3. Third-stage; 사고 위험 예측 모형 개발
결론 및 향후 연구과제

서론

교통사고는 사회적 경제적 측면에서 큰 손실을 초래하며, 사망을 초래한다. 세계보건기구에 따르면 교통사고는 전 세계 주요 사망원인 8위에 해당하며, 연간 135만 명이 교통사고로 사망하고 있다(WHO, 2019). 이에 따라 교통사고에 대한 대책을 마련하는 것이 필요하며, 과거 교통안전 관리는 이력 자료를 바탕으로 사고 위험 구간을 지정하여 관리하는 등 사후 대처에 초점을 맞추어 왔다. 하지만 최근에는 실시간으로 사고 발생 전 교통사고 발생확률을 예측하고 사전에 대응하는 교통안전 관리 전략의 필요성이 증가하고 있으며, 기술의 발전과 교통 빅데이터의 증가로 이를 활용한 실시간 교통사고 예측 연구들이 수행되고 있다(Yu and Abdel-Aty., 2013; Wang et al., 2015; Basso et al., 2018; Wang et al., 2019; Formosa et al., 2020; Huang et al., 2020).

실시간 교통사고 예측모형 개발에서 모형에 사용할 변수의 선택은 중요한 단계 중 하나이다. 예측모형에서 너무 많은 변수를 고려하게 되면 모형의 정확도는 높아질 수 있지만, 지나치게 과적합이 일어나거나 모형의 복잡성이 증가하는 문제가 발생할 수 있다. 따라서 적절한 수의 변수만을 사용하기 위해 사고 위험 예측에 핵심이 되는 중요 변수를 선택하는 절차를 거쳐야 한다. 본 연구에서는 이러한 변수 선택 과정에 있어 머신러닝 기법 중 지도학습과 비지도 학습 방법론을 동시에 고려한 Multi-stage 방법론을 제안하였으며, 이를 통해 사고위험 교통류를 잘 구분할 수 있도록 하는 안전 지표를 선택하고 정확도 높은 사고 위험 예측 모형을 개발하였다. Multi-stage 방법론에서 각 단계는 비지도 학습과 지도학습을 통한 주요 변수 선정, 선정된 주요 변수의 조합 도출, 도출된 변수 조합을 독립변수로 사용한 사고 위험 예측 모형 개발로 이루어져 있다. 첫 번째 단계인 핵심 변수 선별에서는 비지도 학습 방법론 중 K-means Clustering(KC)와 지도학습 방법론 중 Random Forest(RF) 방법론을 사용하여 주요 변수를 도출하였다. KC 방법론의 경우 주로 사고 심각도 모형 개발에 적용되어왔으며, 비지도학습을 통해 사고 데이터를 여러 개의 군집으로 분류함으로써 사고 모형 개발에 지도학습으로는 도출되지 않는 잠재적인 중요 요인을 반영할 수 있다는 장점이 있다(Mohamed et al., 2013). RF 방법론의 경우 학습 과정에서 생기는 노드 불순도를 활용하여 변수들의 중요도 순위를 도출할 수 있다는 장점을 가지고 있다. 두 번째 단계에서는 KC와 RF 방법론을 통해 도출된 변수들의 조합을 구성하였다. 마지막으로, 세 번째 단계에서는 회귀 및 분류모형에 주로 사용되는 머신러닝 기법 중 Support Vector Machine(SVM)을 사용하여 사고위험 교통류와 일반 교통류를 분류하는 사고 위험 예측 모형을 개발하였다. 모형 개발 과정에서 데이터는 사고위험 교통류와 일반교통류 정의에 따라 1:5 비율로 추출하여 사용하였으며, 오차 행렬표를 기반으로 RF로 핵심 변수를 도출하여 개발한 사고위험 예측모형과 KC로 핵심 변수를 도출했을 때의 사고위험 예측모형, RF와 KC 방법론으로부터 도출된 변수를 동시에 사용했을 때의 사고위험 예측모형의 성능을 평가하였다.

이전 연구들에서 검지기 자료 또는 개별차량 데이터를 사용하여 실시간 교통사고 위험을 포착하고, 이에 대응하려는 시도가 있었다(Formosa et al., 2020; Kim et al., 2021). 본 연구에서는 차량의 위험 주행행태를 잘 포착할 수 있도록 하기 위해 사업용 자동차 운행기록장치(Digital Tachograph, DTG)에서 수집된 주행궤적 데이터를 사용하였다. 주행궤적 데이터의 경우 일정한 시간 간격으로 수집된 평균적인 교통류 상태를 나타내는 검지기 데이터와 다르게 급감속, 급가속 등 차량의 불안정적인 주행행태를 포착할 수 있게 한다는 장점을 가지고 있다. 본 연구에서 활용한 DTG 데이터의 시간적 범위는 2017년 3월 5일부터 3월 14일, 12월 한 달. 그리고 2018년 3월 4일부터 3월 23일까지 총 61일이며, 공간적 범위는 한국의 고속도로 전체 범위이다. 1초 단위로 수집되는 DTG 데이터를 기반으로 다양한 변수를 산출했으며, 1분 단위로 집계하여 데이터의 실시간성을 반영하였다.

본 연구의 목적 및 목표는 다음과 같다. 첫 번째로, KC를 통해 사고위험 교통류 군집과 일반교통류 군집을 가장 명확하게 분류하는 핵심 변수를 도출하여 잠재적인 사고 발생 징후 인자(Crash precursor)를 도출하고자 하였다. 두 번째로, 개별차량 주행궤적 데이터를 가공하여 사용함으로써 주행행태 기반 안전 지표들을 사용해 사고위험을 예측할 수 있는 모형을 개발하였다. 세 번째로 RF, KC, RF-KC hybrid 방법으로 도출된 핵심 변수를 독립변수로 한 사고 위험 예측 모형을 개발하고 그 성능을 비교하여 변수 선택을 위한 최적의 방법과 정확도 높은 최종 사고 위험 예측 모형을 제안하였다. 본 연구에서 제안한 Multi-stage 방법론을 통해 보다 정확도 높은 사고 위험 예측 모형을 개발할 수 있다.

선행연구

교통 분야에서는 사전 예방 개념의 선제적 안전 관리 전략의 중요성이 대두되면서 사고위험 예측모형 개발과 관련된 연구들이 수행되어왔다(Abdel-Aty et al., 2004; Abdel-Aty and Pande, 2005; Abdel-Aty et al., 2005; Abdel-Aty et al., 2012; Ahmed and Abdel-Aty, 2013; Yu and Abdel-Aty, 2013; Xu et al., 2014; Lin et al., 2015; Shi and Abdel-Aty, 2015; Wang et al., 2015; You et al., 2017; Basso et al., 2018; Wu et al., 2018; Yang et al., 2018; Wang et al., 2019; Huang et al., 2020; Yuan et al., 2022). Yuan et al.(2022)은 고속도로 사고 위험 예측 모형 개발을 위해 20초 간격으로 수집되는 루프 검지기 데이터를 5분 단위로 집계해 사고 데이터와 매칭하였으며, 사고를 종속변수로, 다양한 교통변수를 독립변수로 한 Bayesian logistic 회귀모형을 개발하였다. 모형 개발 과정에서는 유의한 변수 선정을 위해 Logistic stepwise regression을 수행하였다. Cai et al.(2020)은 차량 검지기 데이터를 활용하여 고속도로 실시간 사고 예측모형을 개발하였다. 사고 예측모형으로 로짓모형(Logit model), SVM, Artificial Neural Network(ANN), Convolution Neural Network(CNN)를 사용하였다. 핵심 변수 선정을 위해서는 Pearson 상관분석과 RF 분석을 수행하였으며, 두 가지 분석 결과를 조합하여 사고 위험 예측 모형에 사용되는 변수를 선별하였다. Cheng et al.(2022)은 루프 검지기로부터 2분 간격으로 수집되는 속도, 교통량 등의 데이터를 활용하여 Extended logit 모형 기반의 사고 위험 예측 모형을 개발하였다. 개발된 로짓 모형의 매개변수 평가를 통해 사고위험 확률을 정량화하였으며, 핵심 변수 선정을 위해 카이 제곱 검정과 다중공선성 검정을 수행하였다. Lei et al.(2021)은 영상검지기로부터 수집한 데이터를 활용하여 머신러닝 기법으로 고속도로 사고를 예측하는 연구를 수행하였다. 모형 개발에 필요한 교통류 변수를 선정하기 위해 RF 기법을 사용하였으며, 사고 분류모형으로 SVM을 사용하였다. Kim et al.(2021)은 한국 DTG로부터 수집된 데이터를 활용하여 사고위험 예측모형을 개발하였다. 사고에 영향을 끼치는 교통류 변수의 우선순위를 도출하기 위해 Gradient Boosting(GB) 기법을 사용하였으며, Neural Network 기반의 사고 위험 예측 모형을 개발하였다. Ahmed and Abdel-Aty(2013)은 사고 위험 예측 모형 개발을 위한 주요 변수 선정을 위해 Stochastic Gradient Boosting(SGB) 방법론을 사용하였으며, 상대적 중요도가 25% 미만인 변수는 모델 개발 단계에서 제외하였다.

기존 연구들은 대부분 사고 위험 예측 모형 개발에 고속도로 등 교통 인프라에 설치되어 있는 검지기 데이터를 활용하였다. 루프 검지기와 같은 검지기 데이터의 경우 다량의 데이터를 수집할 수 있으며 교통류의 특성을 효과적으로 반영할 수 있다는 장점이 있다. 하지만 검지기 기반의 데이터의 경우 실시간으로 변화하는 차량의 주행행태와 위험 상황을 반영하는 데에 어려움이 있다. 따라서 최근에는 영상 자료, GPS 자료 등 개별차량 주행궤적 데이터를 활용하여 실시간으로 사고위험을 예측하는 연구들이 수행되었다. Formosa et al.(2020)은 실시간 Deep Neural Network(DNN) 기반의 사고 위험 예측 연구 모형을 개발하였으며, 차량 내 센서(In-vehicle sensor)로부터 수집되는 차량간 상호작용 정보를 사용하여 안전 대체 지표(Surrogate Safety Measures, SSM)를 산출하여 독립변수로 활용하였다. 그리고 모형 개발 과정에서 변수 선별 없이 26개의 독립변수를 모두 사용하였다. 또한, Kim et al.(2021)의 경우 버스, 택시 등 상업용 차량의 주행궤적 데이터인 DTG 데이터를 사용하여 실시간 사고위험을 평가하는 연구를 수행하였으며, 사고위험 예측에 핵심이 되는 변수 선별을 위해 앙상블 기반의 지도학습 방법론인 Gradient Boosting(GB) 방법론을 적용하였다. Xia et al.(2022)의 경우 영상 자료에서 추출한 차량 들의 주행궤적 데이터를 수집하고 Naive Bayes와 로지스틱 회귀분석, Gradient Boosting Decision Tree 기반의 교통 상충 예측모형을 개발하였다. 이 과정에서 사고위험 예측을 위한 변수로는 개별차량의 속도 기반의 데이터를 사용하였으며, 22개의 변수 후보 중 심각한 다중공선성이 존재하는 변수를 제외한 17개의 변수를 활용하였다. 본 연구에서는 실시간 주행궤적 데이터를 활용하여 사고위험 예측모형을 개발한 기존 연구들과는 다르게 개별차량의 주행 위험을 나타낼 수 있는 안전지표 뿐만 아니라 혼잡지표, 차선 수 등 교통류의 안전성을 나타내는 변수들을 함께 활용하였다. 또한, 고도화된 모형 입력 변수 선별 방법론을 통해 사고위험 예측모형에 핵심이 되는 변수들을 선정하였다.

사고 위험 예측에 관한 기존 연구들은 핵심 변수 선별을 위해 대부분 상관분석 또는 앙상블 기반의 머신러닝 방법론을 사용하였다. 하지만 교통사고는 사고위험 교통류 분류에 핵심이 되는 변수 중 지도학습을 통해 드러나지 않는 중요 변수가 있을 수 있으므로 비지도 학습 시 도출되는 안전 지표가 새로운 핵심 변수가 될 수 있는지 확인해 볼 필요가 있다. 본 연구에서는 고속도로 사고 위험 예측 모형 개발을 위하여 변수 선택과 변수 조합, 모형 개발의 3단계로 절차를 나누어 진행하였으며, 특히 변수 선정 과정에서 비지도 학습과 지도학습으로부터 도출된 주요 변수를 모두 고려하여 교통사고 발생과 관련된 잠재적인 요소를 고려할 수 있는 사고위험 예측모형을 개발하려고 시도하였다. 그리고 고도화된 핵심 변수 선별 방법론을 통하여 적은 입력 변수로도 사고위험 교통류를 정확도 높게 식별할 수 있도록 하는 사고위험 예측모형을 개발하였다. 사고위험 예측모형 개발 연구들에서 사용한 모형과 데이터, 변수 선택 방법론은 Table 1과 같다.

Table 1.

Previous studies in crash risk prediction

Study	Variable selection	Crash prediction	Data
Ahmed and Abdel-Aty(2013)	SGB	SGB	AVI, RTMS
Yu and Abdel-Aty(2013)	CART	SVM	RTMS
Xu et al.(2014)	Pearson’s correlation test	Bayesian LR	Loop detector
Lin et al.(2015)	RF, Free-pattern tree	K-NN, Bayesian network	Traffic detector
Shi and Abdel-Aty(2015)	RF, Pearson’s correlation test	Bayesian LR	MVDS
Wang et al.(2015)	RF, Pearson’s correlation test	Multilevel Bayesian LR	MVDS
You et al.(2017)	RF	SVM	Weather data, Loop detector
Basso et al.(2018)	RF, Pearson’s correlation test	SVM, LR	AVI
Yang et al.(2018)	LR	Bayesian Dynamic LR	Loop detector
Wang et al.(2019)	Bayesian LR	SVM	MVDS
Cai et al.(2020)	Pearson’s correlation test	LR, SVM, ANN, CNN	MVDS
Huang et al.(2020)	-	CNN	Roadside radar sensor
Basso et al.(2021)	Pearson’s correlation test, Boruta algorithm	CNN	AVI
Kim et al.(2021)	GB	Neural Network	Digital tachograph
Lei et al.(2021)	RF	SVM	Video detector
Cheng et al.(2022)	-	Extended LR	Loop detector
Formosa et al.(2020)	-	R-CNN, DNN	In-vehicle sensor, Loopdetector, Camera
Li et al.(2022)	SHAP	XGBoost-Hybrid model	Traffic detector
Xia et al.(2022)	Multicollinearity diagnosis	Naive Bayes, LR, GB, Decision Tree	Vehicle trajectory data
Yuan et al.(2022)	Stepwise LR	Bayesian LR, SVM	Loop detector

*Automatic Vehicle Identification (AVI); Remote Traffic Microwave Sensors (RTMS); Classification And Regression Tree (CART); Rural Traffic Management System (RTMS); Logistic regression (LR); K-nearest neighbor(K-NN); Regional–Convolution Neural Network (R-CNN); Neural Network (NN); SHapley Additive exPlanations (SHAP)

연구방법론

본 연구에서는 고속도로의 실시간 사고위험을 평가하기 위한 Multi-stage 방법론을 제안하였다. 여기서 Multi-stage는 사고 위험 예측 모형에 입력 변수로 활용할 핵심 변수의 선별 과정에 비지도학습 방법론과 지도학습 방법론을 모두 사용한 것을 의미한다. 본 논문에서 Single-stage 방법론의 경우 핵심 변수의 선별 없이 전체 변수를 활용하여 사고 위험 예측 모형을 개발하는 것이고, Two-stage 방법론은 비지도학습 방법론 또는 지도학습 방법론 한 가지를 통해 핵심 변수를 선별하고, 해당 변수로 사고위험 예측모형을 개발하는 것이다. 본 연구에서는 Single-stage 방법론과 Two-stage 방법론, 그리고 제안된 Multi-stage 방법론 기반의 예측모형을 비교하였다. 본 연구의 전체적인 흐름은 Figure 1과 같다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420306/images/kst_2024_423_331_F1.jpg

Figure 1.

Research framework for a crash risk prediction

Multi-stage 방법론 기반의 사고 위험 예측 모형 개발 과정은 다음과 같다. 첫 번째로, 두 가지의 머신러닝 방법론을 사용하여 사고위험 예측모형의 핵심 안전 지표를 선별하였다. KC 방법론을 사용해서는 사고위험 교통류와 일반교통류 군집 분류 후 사고위험 군집과 일반 군집을 효과적으로 분류할 수 있는 변수를 핵심 안전 지표로 도출하였으며, RF에서는 모형 학습 과정에서 노드의 불순도에 따라 나타나는 변수 중요도 리스트를 통해 중요한 안전 지표를 선별하였다. 두 번째 단계는 주요 안전 지표들의 조합을 찾는 것으로, KC와 RF 분석 결과에 따라 도출된 안전 지표들의 조합을 도출하였다. 마지막으로 세 번째 단계에서는 SVM 기반의 사고 위험 예측 모형을 개발하고, 변수 조합별 예측 성능 비교를 통해 핵심 변수 선별에 있어 비지도 학습 및 지도학습의 기여도와 최적의 핵심 변수 조합을 도출하였다.

1. 변수 중요도 도출

본 연구에서는 군집분석 방법론 중 KC와 앙상블 기법의 하나인 RF 방법론을 사용하여 사고 위험 예측 모형 개발을 위한 주요 안전 지표들을 선별하였다.

1) K-means 클러스터링

군집분석은 머신러닝 비지도 학습 기법의 일종으로, 정답(label) 없이 유사한 특성을 갖는 데이터를 군집으로 묶는 방법론이다. 대표적인 군집분석 방법론에는 거리 기반의 군집 분류 방법론인 K-means clustering(KC)가 있다. KC는 주어진 데이터를 K개의 클러스터로 묶는 방법론으로, K는 클러스터의 개수를, means는 클러스터의 중심과 데이터 간의 평균 거리를 의미한다(MacQueen, 1967). 기존 연구에서는 주로 사고 심각도에 영향을 미치는 주요 요인을 도출하기 위해 클러스터링 기법을 사용하였다(Assi et al., 2020). 본 연구에서는 교통류 데이터를 위험 교통류와 일반교통류 두 가지로 구분하였으며, 두 집단을 잘 분류할 수 있는 잠재적인 안전 지표를 도출하기 위해 KC 방법론을 변수 선별 과정에 적용하였다.

KC의 원리는 다음과 같다. 초기에는 임의로 K개의 중심이 설정되어 데이터들을 가장 가까운 중심점이 속해있는 클러스터로 분류한다. 그리고 분류된 클러스터의 중심으로 중심점이 이동하며, 이 과정을 반복하여 결과적으로 K개의 클러스터를 생성한다. 이 과정에서 입력 변수와 각 클러스터 중심 사이의 거리를 계산해야 하며, Equation 1과 같이 유클리드 거리로 계산된다.

(1)

d (x_{i}, c_{j}) = (\sum_{n = 1}^{N} (x_{i n} - c_{j})^{2})^{\frac{1}{2}}

여기서, $x_{i}$ = 입력 변수

$c_{j}$ = 각 클러스터(군집)의 중심

$m$ = 변수의 개수

$N$ = 데이터 수

Objective function을 최소화하는 방향으로 클러스터 중심이 설정되며, Objective function은 Equation 2와 같이 표현된다.

(2)

o b j e c t i v e f u n c t i o n = \sum_{i = 1}^{m} \sum_{f = 1}^{K} d (x_{i}, c_{j})

여기서, $x_{i}$ = 입력 변수

$c_{j}$ = 각 클러스터(군집)의 중심

$m$ = 변수의 개수

$K$ = 클러스터(군집) 수

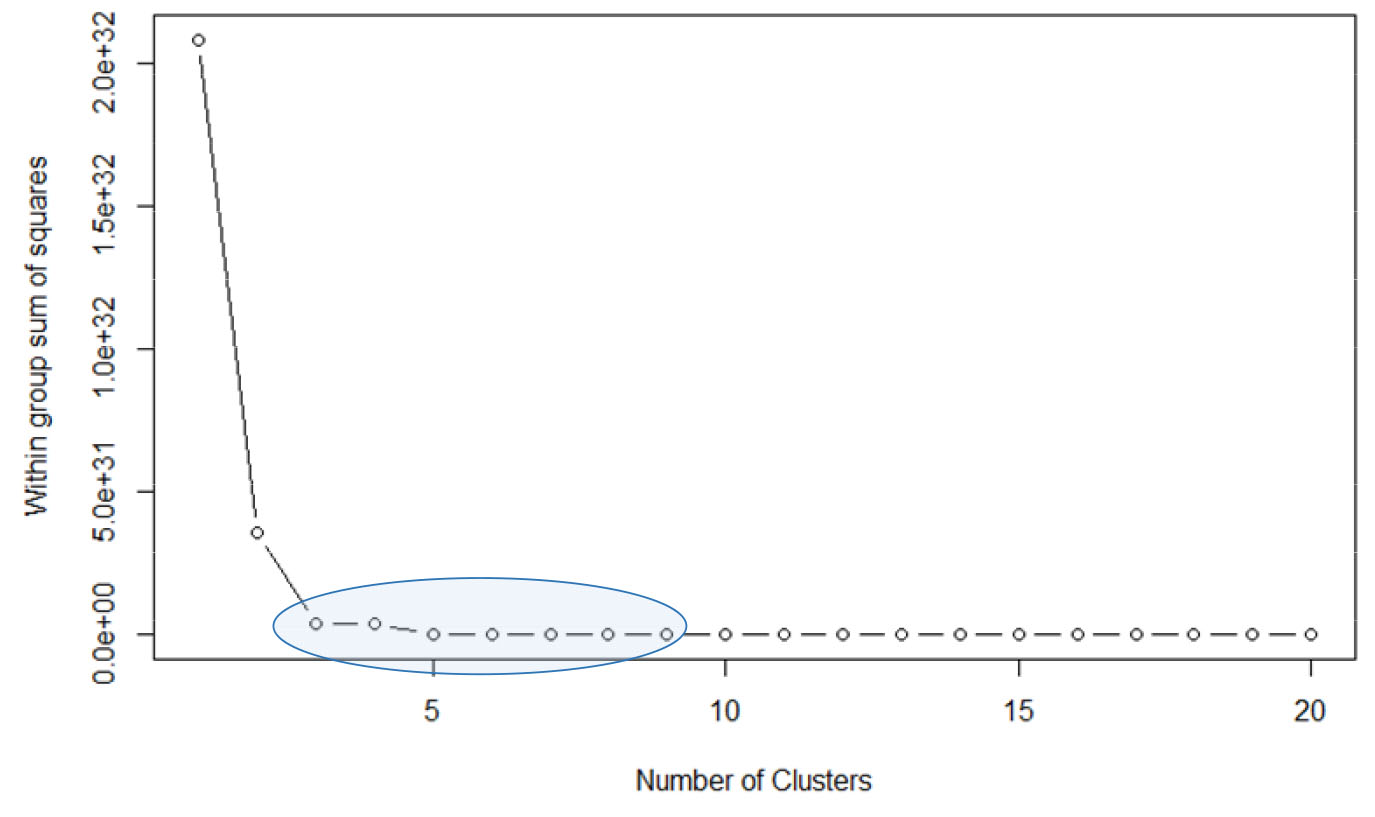
KC에서 K는 사전에 설정되어야 하는 값으로, 본 연구에서는 최적의 K값을 찾기 위하여 Cluster 간의 거리의 합을 나타내는 inertia가 급격히 떨어지는 구간을 찾아 K값을 설정하는 Elbow Method를 사용하였다(Cui, 2020). Elbow Method 결과, K=3부터 기울기가 급격하게 감소하였으며, 본 연구에서는 사고위험 교통류와 일반교통류를 잘 분류하는 최적의 군집 수를 찾기 위해 K=3, K=5, K=7, K=9로 군집 수를 변경하여 분석을 수행하였다.

2) 랜덤포레스트(Random forest, RF)

Random Forest(RF)는 머신 러닝 앙상블 기법의 하나로, 의사결정나무를 여러 개 구축하여 타겟 데이터를 예측하는 데 사용되는 기존 의사결정나무의 문제를 해결하기 위해 개발된 방법론이다(Breiman, 2001). RF 분석을 수행하면 모형 구축 결과와 변수 중요도를 평가하는 척도로 %IncMSE값과 IncNodePurity값을 구할 수 있다. %IncMSE는 해당 변수를 다른 값으로 대체했을 때 Mean squared error(MSE)의 증가 %를 의미하는 척도로, 값이 클수록 중요도가 높은 변수라고 할 수 있다. IncNodePurity는 노드 불순물(node impurity)과 관련된 척도로, node impurity가 증가하면 MSE가 증가한다. 즉, IncNodePurity가 클수록 중요도가 높은 변수이다. 기존 연구들에서 RF 방법론을 사용하여 사고 위험 예측 모형에 활용할 주요 변수를 도출하였으며(Lin et al., 2015; Shi and Abdel-Aty, 2015; Wang et al., 2015; You et al., 2017; Basso et al., 2018; Abou Elassad et al., 2020; Lei et al., 2021), 본 연구에서도 RF 모형 구축 결과 변수 중요도가 높은 안전 지표를 도출하였다.

2. 사고위험 예측모형

사고위험 예측모형으로는 사고위험 교통류와 일반교통류를 분류하는 이진 분류모형을 개발하고자 하였으며, 본 연구에서는 머신러닝 기법 중 서포트벡터머신(Support Vector Machine, SVM)을 활용하였다. SVM은 분류 또는 회귀 분석에 사용할 수 있는 머신러닝 기법으로, 라벨이 포함된 학습데이터를 학습시키는 지도학습 모형이다(Boser et al., 1992). SVM의 이해를 위해서는 초평면(Hyperplane)과 서포트벡터(Support Vector), 마진(Margin)의 개념을 이해해야 한다. 초평면은 데이터를 분류하는 평면이고, 서포트벡터는 이 초평면과 가장 가까운 포인트, 마진은 초평면과 서포트벡터 사이의 거리를 의미한다. SVM은 초평면을 기준으로 데이터를 분류하며, 분류 과정에서 마진을 최대화하는 초평면을 채택하여 데이터를 분류한다.

분석 정확도를 높이기 위해서는 SVM 하이퍼 파라미터 조정이 필요하다. 본 연구에서는 파이썬의 사이킷런(sklearn) 라이브러리를 활용하여 분석을 수행했으며, 그리드 서치를 통해 SVM 모형의 하이퍼파라미터 중 kernel, C, gamma값을 조정하였다. 또한, 모델 훈련과 검증을 위하여 전체 데이터를 훈련 데이터와 검증 데이터 7:3으로 나누어 분석을 수행하였다.

3. 모형성능평가

본 연구에서는 오차 행렬(Confusion matrix)을 기반으로 평가지표를 산출하여 모형의 예측 성능을 평가 및 비교하였다. 오차 행렬은 학습된 모형의 예측 오류가 얼마인지, 어떤 유형의 예측 오류가 발생하는지 나타내는 지표로, 일반교통류를 Negative(0), 사고 위험 교통류를 Positive(1), 옳게 예측한 것을 True, 틀리게 예측한 것을 False라고 할 때 True Negative(TN), False Positive(FP), False Negative(FN), True Positive(TP)로 구성된다.

자료수집

본 연구에서는 사업용 자동차의 운행기록장치(Digital Tachograph, DTG)에서 수집된 주행궤적 데이터를 사용하였다. DTG 데이터는 한국교통안전공단에서 관리하는 데이터로, 1초 단위의 주행궤적 데이터를 기록한다. 데이터 수집의 공간적 범위는 한국 고속도로 전체구간으로, DTG 데이터는 상업용 자동차의 데이터이기 때문에 고속도로 특성상 버스(시내버스, 농어촌버스, 마을버스, 시외버스, 고속버스, 전세버스)와 화물자동차(일반화물자동차, 개별화물자동차)가 각각 48.2%, 43.4%로 높은 비율을 차지하며, 택시(일반택시, 개인택시) 등 기타 차종은 8.4%의 비율을 차지한다. 데이터 수집의 시간적 범위는 2017년 3월 5일부터 3월 14일, 2017년 12월 한 달, 2018년 3월 4일부터 3월 23일까지로, 총 61일간의 데이터를 수집하여 사용하였다. 그리고 같은 기간에 발생한 190건의 고속도로 전체 교통사고를 수집하여 DTG 데이터와 매칭을 수행하였다. 교통사고 자료는 2017년 85건의 샘플과 2018년 105건의 샘플을 활용하였으며, 계절별로 다른 교통 패턴을 고려하기 위해 3월과 12월 자료를 수집하여 사용하였다.

DTG 원시 데이터는 차량 정보, 수집 시점, 주행거리, 속도, 차량 위치 등의 정보를 포함하고 있으며, 이를 가공하여 속도, 가속도, jerk, yaw와 같이 다양한 교통변수를 도출할 수 있다. 본 연구에서는 개별차량의 주행안전성을 평가하기 위해 안전 지표를 개발하고 평가한 이전 연구들(Dingus et al., 2006; Bagdadi and Várhelyi, 2013; Chevalier et al., 2017; Feng et al., 2017; Kamrani et al., 2018; Kim et al., 2018; Kim et al., 2021; Park et al., 2021)을 참고하여 4개의 교통변수를 활용해 산출할 수 있는 안전 지표(Safety indicator)를 산출하여 활용하였다. 한편, 대부분의 안전 지표는 개별차량의 주행 안전성을 나타내는 지표이므로 교통류 상황(특히 혼잡상황)을 반영하기 위해 혼잡지표(Congestion index)를 안전 지표에 추가로 포함했다. 또한, 도로 특성도 고려하기 위해 제한속도와 차선 수를 함께 고려하였다. 본 연구에서 사용한 변수들은 Table 2와 같다.

Table 2.

Variable set

Category	Variable name	Description	Reference
Traffic variables	Speed	$\| s p e e d \| (m / s)$	-
	Acc	$\| a c c e l e r a t i o n \| (m / s^{2})$	-
	Jerk	$\| j e r k \| (m / s^{3})$	-
	Yaw	$\| y a w \| (°)$	-
Road variables	Lane	Number of lanes	-
Road variables	Max_speed	Speed limit	-
Safety indicator	CI	Congestion index	Dias et al.(2009)
	Peak to peak jerk	Peak to peak jerk	Bagdadi and Varhelvi(2013)
	SRI_x (x: speed, acc, jerk, yaw)	Safety reliability index	Kim et al.(2021)
	EDI_x (x: speed, acc, jerk, yaw)	Erratic driving indicator	Kim et al.(2018)
	Dangerous event	Dangerous driving event rate	Korea transportation Safety authority
	RDEs	Rapid deceleration events	Chevalier et al.(2017)
	LNJ_x (x: 1.5, 2, 3, 4, total)	Large negative(-) jerk	Feng et al.(2017)
	LPJ_x (x: 1.5, 2, 3, 4, total)	Large positive(+) jerk	Feng et al.(2017)
	Rapid peak to peak	Rapid peak to peak jerk rate	Bagdadi and Varhelvi(2013)
	Yaw rate	Yaw rate	Dingus et al.(2006) Kamrani et al.(2018)
	S.D_x (x: speed, acc, jerk, yaw)	S.D (Standard deviation)
	TVSV_x (x: speed, acc, jerk, yaw)	Driving volatility, TVSV (Time-varying stochastic volatility)

사고위험 예측모형은 사고위험 교통류와 일반교통류를 분류하는 분류모형으로 구축된다. 기존 연구들에서는 사고 발생 시간대와 공간은 같지만 다른 날짜의 데이터를 비사고 데이터로 추출하거나(Abdel-Aty et al., 2008; Shi and Abdel-Aty, 2015; Zhai et al., 2020) 사고 발생 시점 전 시간대 범위를 설정하여 사고 데이터와 비사고 데이터를 추출하였다(Oh et al., 2005; Hossain et al., 2012; Kim et al., 2021). 또한 기존 연구들에서는 사고 위험 예측을 위해 예측 대상 데이터와 대조군 데이터 간의 비율을 1:5로 설정하여 분석하였다(Lei et al., 2021; Abdel-Aty et al., 2004). 본 연구에서는 사고위험 교통류를 사고 발생 시점에서 1분 전 교통류로, 일반교통류를 사고 발생 시점 10-15분 전 5분간의 교통류로 정의하고 데이터를 추출하였다. 추출된 데이터는 1분 단위로 집계하여 사고위험 교통류 190건, 일반교통류 831건의 분석 데이터를 구축하였다.

분석 결과

본 연구에서는 KC와 RF 분석 결과를 바탕으로 사고 위험 예측 모형의 핵심 변수를 선정하였으며, 이들 조합을 독립변수로 하고 사고위험 여부를 종속변수로 한 SVM 기반 사고 위험 예측 모형을 개발하였다. 본 장에서는 변수 선정 및 조합 결과와 예측모형의 비교 및 최적 변수 조합에 관하여 정리하였다.

1. First-stage; 변수 선택

1) K-means 클러스터링

KC 결과 군집 중 사고위험 교통류가 일반교통류보다 많이 존재하는 ‘사고 probability’가 0.5 이상으로 높은 군집을 사고위험 군집으로 정의하였다. 즉, 사고위험 군집과 일반 군집을 잘 나눌 수 있는 K값을 찾아 클러스터링을 수행하였으며, Elbow method 결과에 따라 K를 3, 5, 7, 9로 바꿔가며 클러스터링을 시행하였다(Figure 2). 이를 위해 38개의 전체 변수 set에서 변수를 하나씩 제거하며 분류된 군집을 확인하였으며, KC 분석 결과 K=7이고 5가지 변수를 사용했을 때 가장 사고위험 교통류 군집과 일반교통류 군집을 잘 분류하는 것으로 나타났다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420306/images/kst_2024_423_331_F2.jpg

Figure 2.

Elbow method results

해당 5가지 변수는 3가지 안전 지표(Peak to peak jerk, RDE, CI)와 2가지 교통변수(Acc, Jerk)이다. Peak to peak jerk의 경우 가가속도(jerk)의 최댓값과 최솟값의 차이로, 해당 지표로 개별차량의 주행 안정성을 판단할 수 있다(Bagdadi and Várhelyi, 2013). RDE의 경우 7.35m/s² 이상의 급격한 감속 이벤트를 나타내는 지표로, 빠른 속도의 교통류가 저속 교통류를 갑작스럽게 마주하면 RDE 이벤트가 발생할 수 있다(Chevalier et al., 2017). 마지막으로 CI의 경우 혼잡지표로, 실제 속도와 자유속도로 정의할 수 있는 지표이다. 혼잡지표의 경우 지정체 상황 또는 혼잡상황을 반영할 수 있다는 장점이 있다(Shi and Abdel-Aty, 2015; Dias et al., 2009).

Table 3은 7개의 군집 별 사고위험 교통류와 일반교통류의 비율, 즉 사고 발생 가능성(Crash probability)를 보여준다. 즉, 군집 1-4의 경우 사고 발생 가능성이 0.5 이상인 사고위험 교통류를 나타낸다.

Table 3.

Risky and general traffic flow in each cluster

Cluster	Basic information		Number of crashes	Crash probability	Category
Cluster	Average speed	Average lanes	Number of crashes
1	78.21	2.81	3	0.500	Risky traffic flow cluster
2	73.80	3.69	25	0.595
3	69.19	2.86	4	0.667
4	64.63	3.65	3	1.000
5	83.85	2.94	89	0.128	General traffic flow cluster
6	80.41	3.49	42	0.219
7	83.29	2.78	24	0.316

2) 랜덤포레스트(Random forest, RF) 결과

전체 데이터와 7개의 군집 별 데이터에서 RF 분석을 수행한 결과, 데이터 수가 매우 적어 RF 분석이 어려운 군집 1, 3, 4를 제외하고 Table 4 와 같이 핵심 변수들이 도출되었다. RF 분석에서 핵심 변수는 RF에서 도출할 수 있는 정확도(%IncMSE) 지표와 중요도(IncNodePurity) 지표를 확인하여 선정하였다. 분석 결과 각 군집 별 핵심 변수와 전체 데이터의 핵심 변수의 중요도 순위가 다르게 도출되었다.

Table 4.

Importance ranking of variables in each RF result

Rank	Entire data	Cluster 2 (risky cluster)	Cluster5	Cluster6	Cluster7
1	Dangerous event	Yaw	Dangerous event	SRI_speed	TVSV_speed
2	Jerk	Dangerous event	Peak to peak jerk	EDI_speed	LNJ_total
3	Rapid peak to peak	LNJ_4	SRI_speed	TVSV_jerk	SRI_jerk
4	Peak to peak jerk	Acc	SRI_acc	Yaw	EDI_jerk
5	Acc	Peak to peak jerk	Jerk	Dangerous event	EDI_acc
6	S.D_speed	Max_speed	SRI_jerk	Lane	S.D_speed
7	EDI_speed	LNJ_3	EDI_speed	S.D_speed	SRI_acc
8	TVSV_jerk	Yaw rate	TVSV_yaw	TVSV_acc	LNJ_1.5
9	Yaw	EDI_acc	TVSV_speed	S.D_acc	Acc
10	TVSV_speed	TVSV_acc	EDI_yaw	SRI_acc	Yaw

2. Second-stage; 변수 조합 생성

본 연구에서는 KC와 RF 분석 결과 도출된 핵심 변수들을 조합하여 사고 위험 예측 모형 개발을 위한 최적의 변수 집합을 찾고자 하였으며, Table 5와 같은 변수 조합에 따라 총 32개의 예측모형을 개발하였다. Table 5에서 Single-stage model의 경우 기존 문헌 고찰을 통해 선별한 38개의 안전 지표를 모두 독립변수로 하여 개발한 모델이고, Two-stage model의 경우 KC 또는 RF 결과 핵심 변수로 도출된 변수들의 조합을 독립변수로 하여 개발한 모델이다. 마지막으로 Multi-stage model의 경우 KC와 RF 방법론을 통해 도출된 핵심 변수들의 조합을 사용하여 개발한 모델로, 모델 13-22의 경우 KC을 통해 도출된 5개의 주요 변수와 RF를 통해 도출된 변수 중 높은 우선순위를 가지는 변수들의 조합으로 구성된다. 예를 들어, 모델 13의 경우, KC에서 도출된 5개의 핵심 변수와 군집 별 데이터에서 RF를 통해 도출된 핵심 변수 중 1순위로 중요한 변수들(Dangerous event, Yaw, SRI_speed, TVSV_speed)의 조합이다. 모델 23-32의 경우 사고위험 교통류 군집인 군집 2에서 RF 분석 결과 우선순위가 높게 도출된 변수와 KC을 통해 도출된 5개의 주요 변수의 조합으로 개발된 모델들이다. 예를 들어, 모델 23의 경우 KC를 통해 도출된 핵심 변수인 Peak to peak jerk, RDE, CI, Acc, Jerk와 군집 2 데이터에서의 RF 분석 결과 가장 중요도가 높은 것으로 도출된 Yaw 변수의 조합으로 개발된 모델이다.

Table 5.

Variable composition by model

Model		Description		Number of variables
Single-stage	1	All variables		38
Two-stage	2	KC results		5
Two-stage	3-12	RF in entire data and select important variables (Add one by one according to rank)		1-10
Multi-stage	13	KC + RF in each cluster and select important variables	(First place)	9
	14		(First to Second place)	11
	15		(First to Third place)	14
	16		(First to Fourth place)	16
	17		(First to Fifth place)	17
	18		(First to Sixth place)	20
	19		(First to Seventh place)	21
	20		(First to Eighth place)	25
	21		(First to Ninth place)	26
	22		(First to Tenth place)	27
	23-32	RF in crash risk cluster 2 and select important variables (Add one by one according to rank)		1-10

3. Third-stage; 사고 위험 예측 모형 개발

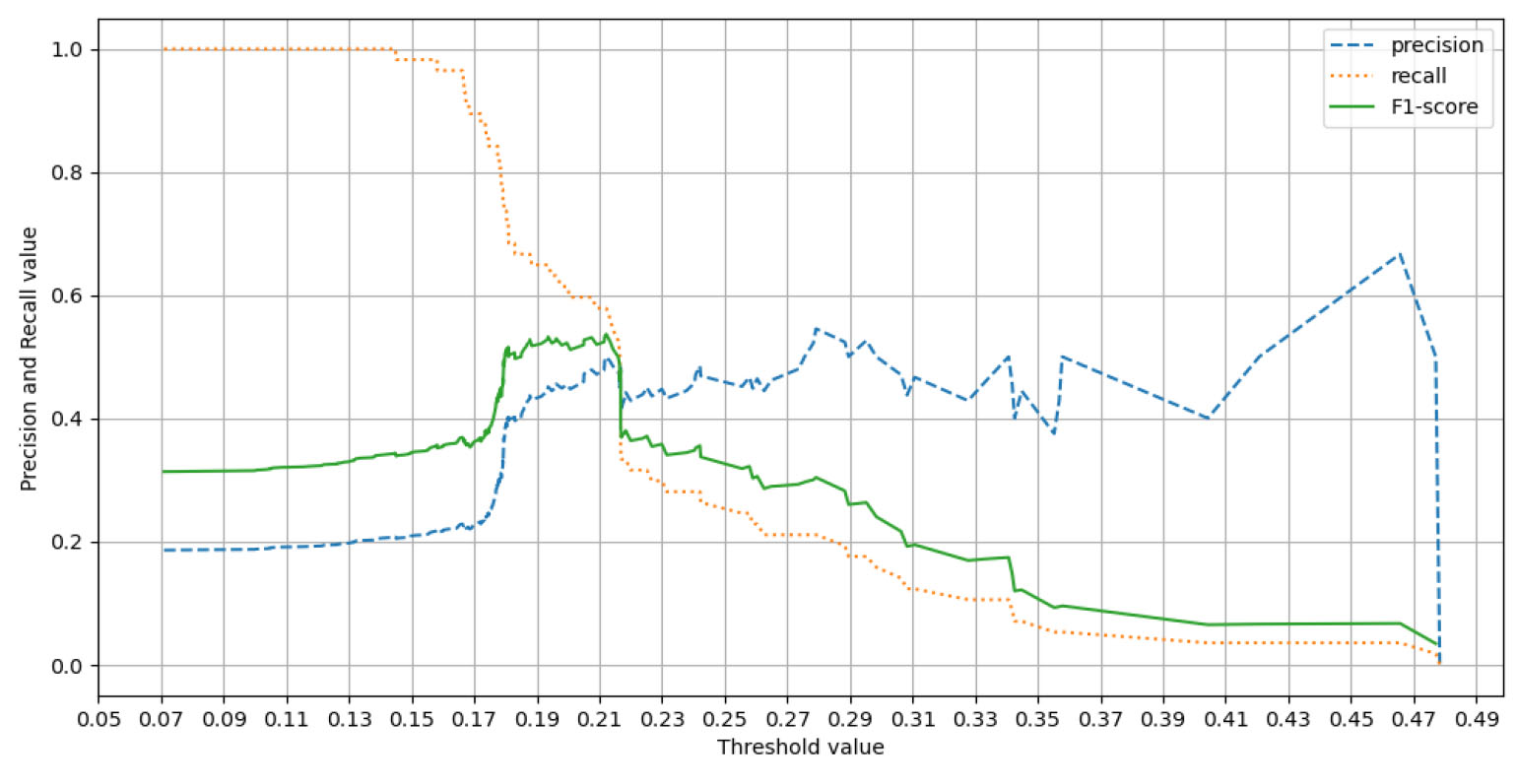
Table 5에 정리된 변수 조합에 따라 SVM 기반의 사고 위험 예측 모형을 개발한 결과는 Table 6과 같다. 종속변수는 사고 위험(사고위험 교통류[1], 일반교통류[0])으로 설정하였으며, 정확도 높은 사고위험 예측모형 개발을 위해 사고위험 교통류를 판단하는 임곗값 기준인 cut-off point를 설정한 기존 연구(Ahmed and Abdel-Aty, 2013; Shi and Abdel-Aty, 2015)를 참고하여 본 연구에서는 default 값인 0.5 대신 다른 값을 사용하였다. 사고 위험 예측 모형 개발에서는 cut-off point가 낮을 때 실제 사고위험 상황을 사고위험 교통류로 예측하는 비율이 높아질 수 있으며, 즉, Recall 값을 높이기 위해 cut-off point를 낮게 조정할 필요가 있다. 예를 들어, 사고위험도가 0.4인 경우 통상적으로 0.5가 분류 기준으로 설정되기 때문에 해당 이벤트는 일반교통 상황으로 분류되지만, cut-off point를 0.3으로 낮출 경우 해당 이벤트는 사고위험 교통 상황으로 분류될 수 있다. 하지만 cut-off point가 너무 낮게 설정되면 실제 사고위험 상황이 아님에도 사고위험 교통 상황으로 분류하는 오경보율이 높아질 수 있으므로 적정한 cut-off point를 찾는 것이 중요하다. 기존 연구들에서는 실시간 사고 위험 예측 연구를 위해 cut-off point 값은 0.08에서 0.22까지 조정하였다(Wang et al., 2015; Shi and Abdel-Aty, 2015; Huang et al., 2017; Wu et al., 2019). 본 연구에서는 적정한 cut-off point를 찾기 위해 먼저 모형의 성능을 평가할 수 있는 Area Under the ROC Curve(AUC)를 산출하였다. 또한, AUC 산출 후 가장 성능이 높게 도출된 모델 7 (AUC 0.768)에 대하여 Figure 3과 같이 precision-recall graph를 도출하였다 (Figure 3). 결과적으로 도출된 모델 7의 precision-recall graph를 기준으로 Precision과 Recall 값의 조합으로 산출되는 F1-score가 급격하게 높아지는 지점인 0.18을 최종 cut-off point로 설정하였다.

Table 6은 각 변수 조합에 따른 사고 위험 예측 모형의 성능을 정리한 것이다. 본 연구에서는 모형 성능이 뛰어난 최적의 모델과 변수 조합을 찾기 위해 다음과 같은 기준을 세우고 가장 성능이 우수하게 도출된 모델을 도출하였다. 첫 번째로, 사고 위험 예측 모형은 일반 교통 상황을 옳게 분류하는 것 보다는 사고위험 상황을 사고위험으로 옳게 분류하는 것이 중요하기 때문에 recall 값이 0.6보다 큰 모델들을 선별하였다. 두 번째로, 모델의 전체적인 정확도가 0.6보다 큰 모델을 선별하였다.

https://cdn.apub.kr/journalsite/sites/kst/2024-042-03/N0210420306/images/kst_2024_423_331_F3.jpg

Figure 3.

Precision-recall graph

Table 6.

Model performance evaluation results

Variable set	Model	Recall	Accuracy	Precision	Variable set	Model	Recall	Accuracy	Precision
Entire	1	0.7544	0.5342	0.2501	KC+RF	17*	0.7719	0.6020	0.2873
KC	2	0.7579	0.5609	0.2653		18	0.7438	0.5883	0.2749
RF	3	0.9789	0.1818	0.1825		19	0.7614	0.5863	0.2768
	4	0.9018	0.2228	0.1811		20	0.7649	0.5629	0.2653
	5	0.5859	0.4775	0.2681		21	0.7719	0.5576	0.2638
	6	0.5298	0.7055	0.3890		22	0.7684	0.5557	0.2623
	7	0.5018	0.7779	0.4184	KC+RF In crash risk cluster	23	1.0000	0.1857	0.1857
	8	0.5263	0.7635	0.3969		24	0.8631	0.2671	0.1849
	9	0.5439	0.7225	0.3455		25	0.6491	0.4736	0.2376
	10	0.5579	0.7401	0.3683		26	0.7754	0.3160	0.1839
	11	0.7895	0.5505	0.2656		27**	0.7333	0.7010	0.3613
	12	0.7088	0.5909	0.2710		28	0.8070	0.5264	0.2570
KC+RF	13	0.7333	0.5980	0.2789		29	0.7754	0.5297	0.2516
	14	0.7544	0.5844	0.2747		30	0.7825	0.5511	0.2633
	15*	0.7544	0.6124	0.2905		31	0.7684	0.5681	0.2686
	16	0.7719	0.5993	0.2859		32	0.7508	0.5518	0.2575

*Recall > 0.6, Accuracy > 0.6

**Recall > 0.7, Accuracy > 0.7 (Best model)

모델 개발 결과, 모델 15, 17, 27이 정확도와 recall 값 모두 0.6 이상으로 높게 나타나 최적 모형 중 하나로 선정되었다. 특히, 세 모델의 경우 recall 값이 각각 0.754, 0.772, 0.733으로 높게 나타났다. 모델 15와 모델 17의 경우 KC와 RF 분석 결과 도출된 핵심 변수 9개를 사용하여 개발된 모형이다. 이는 KC와 RF로부터 도출된 핵심 안전 지표들이 사고 위험 예측 모형의 성능을 높이는 데에 이바지했음을 의미한다. 모델 27의 경우 교통류 군집 중 군집 2에 해당하는 사고 위험 군집 데이터에서 도출된 주요 변수와의 조합으로 개발된 모델이다. 이 모델은 비지도 학습 군집분석을 통해 도출된 다섯 가지 주요 변수들과 사고 위험 군집인 군집 2에서 RF 분석을 수행한 결과 변수 중요도가 높게 도출된 변수를 함께 사용하여 개발되었으며, 모델 27의 recall 값은 모델 15와 모델 17에 비해 낮지만, 정확도와 정밀도 지표가 가장 높은 것으로 나타났다. 따라서 본 연구에서는 모델 27을 최적 모델로 선정하였으며, 해당 모델은 recall 값 0.733, 정확도 0.701의 높은 성능을 보였다.

모델 15의 경우 KC 결과 핵심 변수로 도출된 Peak to peak jerk, RDE, CI, Acc, Jerk와 RF 결과로 도출된 1-3순위의 변수들인 Yaw, Dangerous event, SRI_speed, TVSV_speed, EDI_speed, LNJ_total, LNJ_4, TVSV_jerk, SRI_jerk의 조합으로, 총 14개의 변수 조합으로 개발된 모델이다. 모델 17의 경우 마찬가지로 KC 분석 결과 핵심 변수인 5가지 변수와 RF 결과로 도출된 1-5순위의 변수 조합으로 개발된 모델로, 모델 15에 SRI_acc, EDI_jerk, EDI_acc가 추가된 예측모형이다. 두 모델 모두 속도와 가속도와 관련된 변수들이 다수 포함되었으며, 교통류의 혼잡 정도를 나타내는 혼잡지표 역시 주요 변수로 포함되었다. 모델 27에서 사용된 독립변수는 Dangerous event, Yaw, LNJ_4, Acc, Peak to peak jerk, Yaw, Jerk로, 급가속과 가속도의 변화 등 차량의 주행 안정성을 나타내는 지표들이 주요 안전 지표로 도출되었다. 또한, 한국교통안전공단에서 정의하고 있는 위험 운전 행동 이벤트인 Dangerous event가 주요 변수 중 하나로 나타나 사고 위험 예측에 있어 과속, 급가속, 급감속과 같은 차량 위험 운전 행동 이벤트를 고려할 필요가 있음을 시사하였다.

또한, 본 연구의 결과를 통해 Table 6과 같이 KC에서 선정된 핵심 변수와 RF 분석에서 도출된 중요도가 높은 변수를 결합할 때 모델의 성능이 향상되는 것을 알 수 있었다. 그뿐만 아니라 모델링 결과는 사고 위험 예측 모델 개발에 필요한 주요 변수를 도출하기 위해 사고위험 교통류 군집인 군집 2 데이터와 함께 RF 분석을 사용할 때 예측 모델의 성능이 향상되었음을 나타내었다. 즉, 본 연구에서 제안한 Multi-stage 방법론 기반의 사고 위험 예측 모델은 Single-stage 및 Two-stage 방법론 기반 모델보다 우수한 성능을 보인다.

결론 및 향후 연구과제

본 연구에서는 사고위험 예측모형 개발을 위해 사업용 개별차량 주행 궤적 데이터를 사용했으며, 사고위험 교통류와 일반교통류를 1:5 비율로 추출하였다. 주행궤적 데이터는 특정 시간 단위로 집계되는 검지기 데이터와 다르게 1초 간격으로 위치정보를 수집하기 때문에 Yaw, Jerk와 같이 보다 다양한 정보를 생성할 수 있다. 이러한 DTG 데이터를 활용해 기존 문헌에서 사용하던 총 38개의 안전 지표를 산출하였으며, 38개의 안전 지표 중 사고위험 예측모형에 독립변수로 사용할 핵심 변수를 도출하기 위하여 K=7로 한 KC와 앙상블 기법의 하나인 RF 분석을 수행하였다. 클러스터링 수행 결과 1-4번 군집은 사고위험 군집으로, 5-7번 군집을 일반교통류 군집으로 도출되었다. 클러스터링 결과를 바탕으로 사고위험 교통류와 일반교통류를 가장 잘 분류한 상황에서 사용된 변수, 각 군집 내에서의 핵심 변수, Random forest로 변수 우선순위를 도출했을 때의 중요도 높은 변수로 SVM 기반의 사고위험 예측(분류) 모형을 개발하고 그 성능을 비교하였다.

Accuracy와 Recall 비교 결과, 비지도 학습을 통해 도출한 변수들과 비지도 학습으로 도출된 군집 별 RF를 수행했을 때 우선순위가 높게 나온 변수들을 함께 사용한 모델 15, 17, 27의 성능이 우수한 것으로 나타났으며, 7개의 군집 중 사고위험군집(군집 2) 내에서 RF를 수행하여 우선순위가 높은 변수를 사용했을 때 Recall, Accuracy 값이 모두 0.7 이상으로 높게 나타났다. 이러한 결과를 통해 사고 위험 예측 시 모형의 성능을 높이기 위하여 군집분석을 통해 잠재적인 사고위험 특성과 사고위험 판단에 효과적인 변수를 도출하는 작업의 필요성을 확인할 수 있다. 비지도 학습 과정을 통해 잠재적 핵심 변수를 도출할 수 있다. 본 연구에서 개발한 방법론은 한국 고속도로의 실시간 사고 위험 예측에 활용할 수 있으며, 이를 통해 선제적인 안전 관리와 빠른 대응이 가능할 것으로 예상된다.

하지만 본 연구는 다음과 같은 한계점과 향후 연구과제가 존재한다. 첫 번째로 DTG 데이터 특성의 문제이다. DTG의 경우 공공기관에서 배포하고 있는 자료로, 자료의 구득이 비교적 쉽지만 사업용 차량에만 부착되어 차량 주행궤적 데이터를 수집하기 때문에 DTG 데이터는 교통류의 전체적인 특성을 반영하기 어렵다는 문제가 있다. 따라서 향후 민간 내비게이션 데이터 등 일반 차량의 주행 궤적 데이터의 구득이 가능하다면 함께 사용하여 사고위험 예측모형을 개발할 필요가 있다. 두 번째로 본 연구에서는 개별차량의 주행행태를 잘 포착하기 위해 DTG 데이터를 활용하였으나, 교통류의 사고위험과 무관한 졸음운전, 차량고장 사고 등으로 인한 사고위험까지 예측하기에는 한계가 존재할 수 있었다. 예를 들어, 예측하고 예방할 수 없는 사고에 대해서는 해당 사고 자체를 예측하는 것 보다는 그 사고로 인한 2차 사고 등을 방지하기 위해 노력하는 것이 더 중요할 수 있다. 따라서 향후 연구에서는 사고 유형을 구분하여 그에 맞는 사고위험 예측모형을 구축하고 안전 관리에 활용할 수 있는 방안을 제시할 필요가 있다. 또한, 우리나라의 전체적인 교통사고 특성을 반영할 수 있도록 사고 샘플링을 수행할 필요가 있다. 세 번째로 본 연구에서는 SVM을 사용하여 사고위험 교통류 분류 모형을 개발하였으나, Recall과 정확도 확인 결과 예측 성능이 뛰어나지 않은 것으로 나타났다. 따라서 보다 높은 정확도의 사고위험 예측모형 개발을 위해 신경망(Neural network), MARS 등 보다 다양한 모형을 개발하여 평가 및 비교해 볼 필요가 있으며, 변수 선택 과정에서도 모형이 과적합되거나 오류가 발생하지 않도록 변수 간 상관관계를 검토하고 모형 예측에 핵심 변수만을 사용할 필요가 있다. 네 번째로, 본 연구에서는 적절한 K값을 Elbow method를 통해 도출하고, 홀수개의 K를 사용하여 사고 군집을 분류하고, 사고위험 교통류에 해당하는 군집과 일반 교통류에 해당하는 군집을 결정하였으나, K값에 따라 군집의 특성이 달라질 수 있으므로 NbClust 등 다른 방법론을 사용하여 K값을 도출하고, 군집 분류를 수행할 필요가 있다. 마지막으로 본 연구에서는 COVID-19 발생의 영향을 받지 않는 연도의 약 2달간의 데이터를 사용하였으나, 더 많은 최신 데이터를 확보하여 정확성과 신뢰성 높은 모형을 개발할 필요가 있다.

Funding

This work is supported by the Korea Agency for Infrastructure Technology Advancement grant funded by the Ministry of Land, Infrastructure and Transport (Grant RS-2022-00142565).

알림

본 논문은 2024 Transportation Research Board 103rd Annual Meeting(2023.01.09)에서 발표된 내용을 수정.보완하여 작성된 것입니다.

References

Abdel-Aty M. A., Hassan H. M., Ahmed M., Al-Ghamdi A. S. (2012), Real-time Prediction of Visibility Related Crashes, Transportation Research Part C: Emerging Technologies, 24, 288-298.

10.1016/j.trc.2012.04.001

Abdel-Aty M., Pande A. (2005), Identifying Crash Propensity using Specific Traffic Speed Conditions, Journal of Safety Research, 36(1), 97-108.

10.1016/j.jsr.2004.11.00215752487

Abdel-Aty M., Pande A., Das A., Knibbe W. J. (2008), Assessing Safety on Dutch Freeways with Data from Infrastructure-based Intelligent Transportation Systems, Transportation Research Record, 2083(1), 153-161.

10.3141/2083-18

Abdel-Aty M., Uddin N., Pande A. (2005), Split Models for Predicting Multivehicle Crashes during High-speed and Low-speed Operating Conditions on Freeways, Transportation Research Record, 1908(1), 51-58.

10.1177/0361198105190800107

Abdel-Aty M., Uddin N., Pande A., Abdalla M. F., Hsia L. (2004), Predicting Freeway Crashes from Loop Detector Data by Matched Case-control Logistic Regression, Transportation Research Record, 1897(1), 88-95.

10.3141/1897-12

Abou Elassad Z. E., Mousannif H., Al Moatassime H. (2020), A Real-time Crash Prediction Fusion Framework: An Imbalance-aware Strategy for Collision Avoidance Systems, Transportation Research Part C: Emerging Technologies, 118, 102708.

10.1016/j.trc.2020.102708

Ahmed M., Abdel-Aty M. (2013), A Data Fusion Framework for Real-time Risk Assessment on Freeways, Transportation Research Part C: Emerging Technologies, 26, 203-213.

10.1016/j.trc.2012.09.002

Assi K., Rahman S. M., Mansoor U., Ratrout N. (2020), Predicting Crash Injury Severity with Machine Learning Algorithm Synergized with Clustering Technique: A Promising Protocol, International Journal of Environmental Research and Public Health, 17(15), 5497.

10.3390/ijerph1715549732751470PMC7432564

Bagdadi O., Várhelyi A. (2013), Development of a Method for Detecting Jerks in Safety Critical Events, Accident Analysis & Prevention, 50, 83-91.

10.1016/j.aap.2012.03.03223200443

Basso F., Basso L. J., Bravo F., Pezoa R. (2018), Real-time Crash Prediction in an Urban Expressway using Disaggregated Data, Transportation Research Part C: Emerging Technologies, 86, 202-219.

10.1016/j.trc.2017.11.014

Basso F., Pezoa R., Varas M., Villalobos M. (2021), A Deep Learning Approach for Real-time Crash Prediction using Vehicle-by-vehicle Data, Accident Analysis & Prevention, 162, 106409.

10.1016/j.aap.2021.10640934600313

Boser B. E., Guyon I. M., Vapnik V. N. (1992), A Training Algorithm for Optimal Margin Classifiers, In Proceedings of the Fifth Annual Workshop on Computational Learning Theory, 144-152.

10.1145/130385.130401

Breiman L. (2001), Random Forests, Machine Learning, 45, 5-32.

10.1023/A:1010933404324

Cai Q., Abdel-Aty M., Yuan J., Lee J., Wu Y. (2020), Real-time Crash Prediction on Expressways using Deep Generative Models, Transportation Research Part C: Emerging Technologies, 117, 102697.

10.1016/j.trc.2020.102697

Cheng Z., Yuan J., Yu B., Lu J., Zhao Y. (2022), Crash Risks Evaluation of Urban Expressways: A Case Study in Shanghai, IEEE Transactions on Intelligent Transportation Systems, 23(9), 15329-15339.

10.1109/TITS.2022.3140345

Chevalier A. et al. (2017), Predictors of Older Drivers' Involvement in Rapid Deceleration Events, Accident Analysis & Prevention, 98, 312-319.

10.1016/j.aap.2016.10.01027810673

Cui M. (2020), Introduction to the K-means Clustering Algorithm Based on the Elbow Method, Accounting, Auditing and Finance, 1(1), 5-8.

Dias C., Miska M., Kuwahara M., Warita H. (2009), Relationship between Congestion and Traffic Accidents on Expressways: An Investigation with Bayesian Belief Networks, In Proceedings of 40th Annual Meeting of Infrastructure Planning (JSCE).

Dingus, T. A. et al. (2006), The 100-car Naturalistic Driving Study, Phase Ii-results of the 100-car Field Experiment, United States, Department of Transportation, National Highway Traffic Safety Administration, No. DOT-HS- 810-593.

10.1037/e624282011-001

Feng F., Bao S., Sayer J. R., Flannagan C., Manser M., Wunderlich R. (2017), Can Vehicle Longitudinal Jerk be used to Identify Aggressive Drivers? An Examination using Naturalistic Driving Data, Accident Analysis & Prevention, 104, 125-136.

10.1016/j.aap.2017.04.01228499141

Formosa N., Quddus M., Ison S., Abdel-Aty M., Yuan J. (2020), Predicting Real-time Traffic Conflicts using Deep Learning, Accident Analysis & Prevention, 136, 105429.

10.1016/j.aap.2019.10542931931409

Hossain M., Muromachi Y. (2012), A Bayesian Network Based Framework for Real-time Crash Prediction on the Basic Freeway Segments of Urban Expressways, Accident Analysis & Prevention, 45, 373-381.

10.1016/j.aap.2011.08.00422269521

Huang T., Wang S., Sharma A. (2020), Highway Crash Detection and Risk Estimation using Deep Learning, Accident Analysis & Prevention, 135, 105392.

10.1016/j.aap.2019.10539231841865

Huang Z., Gao Z., Yu R., Wang X., Yang K. (2017), Utilizing Latent Class Logit Model to Predict Crash Risk, In 2017 IEEE/ACIS 16th International Conference on Computer and Information Science (ICIS), 161-165, IEEE.

10.1109/ICIS.2017.7959987

Kamrani M., Arvin R., Khattak A. J. (2018), Extracting Useful Information from Basic Safety Message Data: An Empirical Study of Driving Volatility Measures and Crash Frequency at Intersections, Transportation Research Record, 2672(38), 290-301.

10.1177/0361198118773869

Kim Y., Oh C., Choe B., Choi S., Kim K. (2018), Development of a Methodology for Detecting Intentional Aggressive Driving Events using Multi-agent Driving Simulations, J. Korean Soc. Transp., 36(1), Korean Society of Transportation, 51-65.

10.7470/jkst.2018.36.1.051

Kim Y., Park J., Oh C. (2021), A Crash Prediction Method Based on Artificial Intelligence Techniques and Driving Behavior Event Data, Sustainability, 13(11), 6102.

10.3390/su13116102

Lei T., Peng J., Liu X., Luo Q. (2021), Crash Prediction on Expressway Incorporating Traffic Flow Continuity Parameters Based on Machine Learning Approach, Journal of Advanced Transportation, 8820402.

10.1155/2021/8820402

Li P., Abdel-Aty M. (2022), A Hybrid Machine Learning Model for Predicting Real-time Secondary Crash Likelihood, Accident Analysis & Prevention, 165, 106504.

10.1016/j.aap.2021.10650434844080

Lin L., Wang Q., Sadek A. W. (2015), A Novel Variable Selection Method Based on Frequent Pattern Tree for Real-time Traffic Accident Risk Prediction, Transportation Research Part C: Emerging Technologies, 55, 444-459.

10.1016/j.trc.2015.03.015

MacQueen J. (1967, June), Some Methods for Classification and Analysis of Multivariate Observations, In Proceedings of the Fifth Berkeley Symposium on Mathematical Statistics and Probability, 1(14), 281-297.

Mohamed M. G., Saunier N., Miranda-Moreno L. F., Ukkusuri S. V. (2013), A Clustering Regression Approach: A Comprehensive Injury Severity Analysis of Pedestrian-vehicle Crashes in New York, US and Montreal, Canada, Safety science, 54, 27-37.

10.1016/j.ssci.2012.11.001

Oh C., Oh J. S., Ritchie S. G. (2005), Real-time Hazardous Traffic Condition Warning System: Framework and Evaluation, IEEE Transactions on Intelligent Transportation Systems, 6(3), 265-272.

10.1109/TITS.2005.853693

Park S., Son S. O., Park J., Oh C., Hong S. (2021), Using Vehicle Data as a Surrogate for Highway accident Data, In Proceedings of the Institution of Civil Engineers-Municipal Engineer, 174(2), 67-74, Thomas Telford Ltd.

10.1680/jmuen.20.00012

Shi Q., Abdel-Aty M. (2015), Big Data Applications in Real-time Traffic Operation and Safety Monitoring and Improvement on Urban Expressways, Transportation Research Part C: Emerging Technologies, 58, 380-394.

10.1016/j.trc.2015.02.022

Wang L., Abdel-Aty M., Lee J., Shi Q. (2019), Analysis of Real-time Crash Risk for Expressway Ramps using Traffic, Geometric, Trip Generation, and Socio-demographic Predictors, Accident Analysis & Prevention, 122, 378-384.

10.1016/j.aap.2017.06.00328689932

Wang L., Abdel-Aty M., Shi Q., Park J. (2015), Real-time Crash Prediction for Expressway Weaving Segments, Transportation Research Part C: Emerging Technologies, 61, 1-10.

10.1016/j.trc.2015.10.008

World Health Organization (2019), Global Status Report on Road Safety 2018, World Health Organization.

Wu M., Shan D., Wang Z., Sun X., Liu J., Sun M. (2019), A Bayesian Network Model for Real-time Crash Prediction Based on Selected Variables by Random Forest, In 2019 5th International Conference on Transportation Information and Safety (ICTIS), 670-677, IEEE.

10.1109/ICTIS.2019.8883694

Wu Y., Abdel-Aty, M., Cai, Q., Lee, J., Park, J. (2018), Developing an Algorithm to Assess the Rear-end Collision Risk under Fog Conditions using Real-time Data, Transportation Research Part C: Emerging Technologies, 87, 11-25.

10.1016/j.trc.2017.12.012

Xia Y., Qin Y., Li X., Xie J. (2022), Risk Identification and Conflict Prediction from Videos Based on TTC-ML of a Multi-lane Weaving Area, Sustainability, 14(8), 4620.

10.3390/su14084620

Xu C., Wang W., Liu P., Guo R., Li Z. (2014), Using the Bayesian Updating Approach to Improve the Spatial and Temporal Transferability of Real-time Crash Risk Prediction Models, Transportation Research Part C: Emerging Technologies, 38, 167-176.

10.1016/j.trc.2013.11.020

Yang K., Wang X., Yu R. (2018), A Bayesian Dynamic Updating Approach for Urban Expressway Real-time Crash Risk Evaluation, Transportation Research Part C: Emerging Technologies, 96, 192-207.

10.1016/j.trc.2018.09.020

You J., Wang J., Guo J. (2017), Real-time Crash Prediction on Freeways using Data Mining and Emerging Techniques, Journal of Modern Transportation, 25(2), 116-123.

10.1007/s40534-017-0129-7

Yu R., Abdel-Aty M. (2013), Utilizing Support Vector Machine in Real-time Crash Risk Evaluation, Accident Analysis & Prevention, 51, 252-259.

10.1016/j.aap.2012.11.02723287112

Yuan Z., He K., Yang Y. (2022), A Roadway Safety Sustainable Approach: Modeling for Real-time Traffic Crash with Limited Data and Its Reliability Verification, Journal of Advanced Transportation, 1570521.

10.1155/2022/1570521

Zhai B., Lu J., Wang Y., Wu B. (2020), Real-time Prediction of Crash Risk on Freeways under Fog Conditions, International Journal of Transportation Science and Technology, 9(4), 287-298.

10.1016/j.ijtst.2020.02.001

Journal of Korean Society of Transportation ISSN:1229-1366(Print) 2234-4217(Online) 대한교통학회지

Preview

Multi-Stage Machine Learning Approach to Assess Crash Risk Using Vehicle Maneuver Data

ABSTRACT

MAIN

Table 1.

Previous studies in crash risk prediction

Figure 1.

Research framework for a crash risk prediction

(1)

(2)

Table 2.

Variable set

Figure 2.

Elbow method results

Table 3.

Risky and general traffic flow in each cluster

Table 4.

Importance ranking of variables in each RF result

Table 5.

Variable composition by model

Figure 3.

Precision-recall graph

Table 6.

Model performance evaluation results

Funding

알림

References